Индуктивность – это коэффициент пропорциональности между электрическим током, протекающим по замкнутому контуру, и магнитным потоком через поверхность, ограниченную контуром.
Математическая формула, соответствующая этому определению:
Ф = L*I
где Ф – магнитный поток,
L – индуктивность,
I – сила тока.
Это классическое определение индуктивности, принятое на начальном этапе изучения электромагнитных явлений. В нем отражено одно из проявлений индуктивности. Познакомившись с ним, можно подумать, что индуктивность – свойство небольшого класса объектов, неких замкнутых контуров, создающих магнитное поле. Это не так; проявления индуктивности многообразны, и мы сталкиваемся с ними в повседневной жизни, зачастую не сознавая этого.
В девятнадцатом веке ученые только начинали изучать электромагнитные явления. Понятие индуктивности, как особого свойства электропроводящего контура, сформулировано в 1886 году, при изучении постоянного тока.
Правило Ленца и индуктивность
Электрический ток создает магнитное поле – это была сенсация в девятнадцатом веке. Электрические и магнитные явления представлялись в прошлом совершенно разными явлениями, и открытие связи между ними вызвало горячий интерес исследователей. Магнитное поле казалось многоликим, присущим совершенно разным объектам – куску магнитной руды, Земному шару и… проводу с током. Сейчас известно, что в каждом из этих объектов магнитное поле порождается движением электрического заряда.
В современной науке установлена общая природа электрического и магнитного полей. При изучении постоянного тока был сделан первый шаг к пониманию этой истины – открыта связь между током и магнитным полем, между силой тока и силой создаваемого им магнитного поля.
Символ L, которым обозначается индуктивность, выбран в честь физика Эмиля Ленца. Он изучал магнитные явления, возникающие при протекании электрического тока. Сила Ленца – это сила, действующая на проводник с током, помещенный в магнитное поле.
Ленц также наблюдал, как катушки из электрических проводов, по которым пропускался ток, притягивались или отталкивались, подобно постоянным магнитам. Притяжение или отталкивание? Это определялось направлением тока в витках, взаимным расположением катушек. А сила взаимодействия определялась количеством витков и силой тока. При одинаковом токе, катушка с большим числом витков создавала большее магнитное поле.
Основные свойства и характеристики магнитного поля.
Электромагнетизм
Магнитное поле
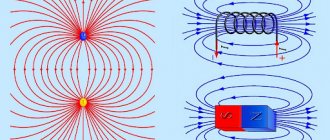
— это материя, которая возникает вокруг источников электрического тока, а также вокруг постоянных магнитов (рис.1.1). В пространстве магнитное поле отображается как совокупление сил, которые способны оказать воздействие на намагниченные тела. Это действие объясняется наличием движущих разрядов на молекулярном уровне.
Рис. 1.1
Магнитное поле формируется только вокруг электрических зарядов, которые находятся в движении. Именно поэтому магнитное и электрическое поле являются, неотъемлемыми и вместе формируют электромагнитное поле
. Компоненты магнитного поля взаимосвязаны и воздействуют друг на друга, изменяя свои свойства.
Свойства магнитного поля:
1. Магнитное поле возникает под воздействие движущих зарядов электрического тока. 2. В любой своей точке магнитное поле характеризуется вектором физической величины под названием
магнитная индукция
, которая является силовой характеристикой магнитного поля. 3. Магнитное поле может воздействовать только на магниты, на токопроводящие проводники и движущиеся заряды. 4. Магнитное поле может быть постоянного и переменного типа 5. Магнитное поле измеряется только специальными приборами и не может быть воспринятым органами чувств человека. 6. Магнитное поля является электродинамическим, так как порождается только при движении заряженных частиц и оказывает влияние только на заряды, которые находятся в движении. 7. Заряженные частицы двигаются по перпендикулярной траектории.
Размер магнитного поля зависит от скорости изменения магнитного поля. Соответственно этому признаку существуют два вида магнитного поля: динамичное магнитное
поле
и
гравитационное магнитное поле
.
Гравитационное магнитное поле
возникает только вблизи элементарных частиц и формируется в зависимости от особенностей строения этих частиц.
Магнитный момент возникает в том случае, когда магнитное поле воздействует на токопроводящую раму. Другими словами, магнитный момент — это вектор, который расположен на ту линию, которая идет перпендикулярно раме.
Магнитное поле можно изобразить графически с помощью магнитных силовых линий. Эти линии проводятся в таком направлении, так чтобы направление сил поля совпало с направлением самой силовой линии. Магнитные силовые линии являются непрерывными и замкнутыми одновременно.
Направление магнитного поля определяется с помощью магнитной стрелки. Силовые линии определяют также полярность магнита, конец с выходом силовых линий — это северный полюс, а конец, с входом этих линий, это южный полюс.
Очень удобно наглядно оценить магнитное поле с помощью обычных железных опилок и листка бумаги. Если мы на постоянный магнит положим лист бумаги, а сверху насыпим опилок, то частички железа выстроятся соответственно силовым линиям магнитного поля.
Направление силовых линий для проводника удобно определять по знаменитому правилу буравчика
или
правилу правой руки
(рис.1.2)
.
Если мы обхватим проводник рукой так, чтобы большой палец смотрел по направлению тока (от плюса к минусу), то 4 оставшиеся пальцы покажут нам направление силовых линий магнитного поля.
Рис. 1.2
· Закон Ампера
Закон Ампера
показывает, с какой силой действует магнитное поле на помещенный в него проводник. Эту силу также называют силой Ампера.
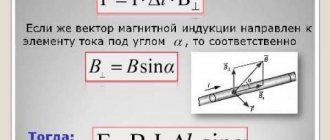
Формулировка закона: сила, действующая на проводник с током, помещенный в однородное магнитное поле, пропорциональна длине проводника, вектору магнитной индукции, силе тока и синусу угла между вектором магнитной индукции и проводником.
Энергия, заключенная в магнитном поле, может проявлять себя в виде электромагнитных сил, которые возникают при взаимодействии магнитного поля с движущимися электрическими зарядами
50
Если поместить в магнитное поле проводник с током I, то между электронами, проходящими по проводнику, и магнитным полем возникнут электромагнитные силы, которые, складываясь, образую т результирующую силу F, стремящуюся вытолкнуть проводник из магнитного поля. Электромагнитная сила F, действующая на проводник с током, находящийся в магнитном поле и расположенный перпендикулярно направлению поля, равна произведению силы тока I, индукции магнитного поля В и длины проводника :
.
Если проводник расположен под углом α к силовым магнитным, то сила, Н,
.
Направление действия силы F обычно определяют по правилу левой руки (рис.1.3).
Рис. 1.3
В результате воздействия таких механических сил при одинаковом направлении тока лежащие рядом проводники будут притягиваться друг к другу (рис. 1.4, а), при разном направлении тока — отталкиваться (рис. 1.4, б). На явлении взаимодействия магнитного поля и проводника с током основано устройство различных электрических машин и приборов, например, измерительных приборов магнитоэлектрической системы. Особенно большие силы между проводниками возникают в электрических цепях при коротких замыканиях.
а) б)
Рис. 1.4 Взаимодействие двух проводников с током: а) при одинаковом направлении тока; б) при разном направлении тока
· Характеристики магнитного поля
Магнитная индукция. Интенсивность магнитного поля характеризуется магнитной индукцией В. Чем сильнее магнитное поле, созданное постоянным магнитом или электромагнитом, тем большую индукцию оно имеет. Направление действия электромагнитной силы F на проводник определяется правилом левой руки (рис. 1.3).
Если расположить левую руку так, чтобы магнитные линии пронизывали ладонь, а вытянутые четыре пальца указывали направление тока в проводнике, то отогнутый большой палец укажет направление действия электромагнитной силы.
По этой силе можно судить об интенсивности магнитного поля, т. е. о его магнитной индукции. Если на проводник длиной 1 м с током 1 А, расположенный перпендикулярно магнитным линиям в равномерном магнитном поле, действует сила в 1 Н, то магнитная индукция такого поля равна 1 Тл (тесла).
Магнитная индукция
— векторная величина
: в каждой точке поля вектор магнитной индукции направлен по касательной к магнитным силовым линиям.
Магнитный поток. Величина, измеряемая произведением магнитной индукции В на площадь S, перпендикулярную вектору магнитной индукции, называется магнитным потоком Ф:
Ф=BS.
Магнитную индукцию выражают в теслах, а площадь — в квадратных метрах, поэтому единица магнитного потока — вебер:
1 Вб = 1 Тл ∙ 1
Магнитодвижущая сила
. Способность тока возбуждать магнитное поле характеризуется
магнитодвижущей силой (МДС)
, Действующей вдоль замкнутой магнитной силовой линии. Магнитодвижущая сила Равна току, создающему магнитное поле, и выражается в амперах.
Для проводника с током I МДС равна току I. В общем случае, когда замкнутый контур магнитной силовой линии охватывает несколько токов, суммарная МДС равна сумме токов.
Для катушки с числом витков w и током I (рис.1.5) МДС равна
ƩI=Iw.
Напряженность магнитного поля
. Магнитодвижущая сила, приходящаяся на единицу длины магнитной силовой линии, называется
напряженностью магнитного
поля Н и выражается в амперах на метр (А/м).
Если физические условия вдоль всей длины I магнитной линии одинаковы, то
.
Например, вокруг прямолинейного проводника с током I линии магнитного поля представляют собой концентрические окружности переменного радиуса х, длина каждой из которых I = 2 х. В этом случае напряженность.
.
По мере удаления от проводника напряженность поля снижается.
Рис. 1.5. Тороидальная катушка
Магнитная проницаемость
. Магнитная индукция зависит не только от силы тока, проходящего по прямолинейному проводнику или индуктивной катушке, но и от свойств среды, в которой создается магнитное поле. Величиной, характеризующей магнитные свойства среды, служит
абсолютная магнитная проницаемость
. Она определяется отношением магнитной индукции В к напряженности магнитного поля Н и измеряется в генри на метр (Гн/м):
.
Абсолютная магнитная проницаемость вакуума = 4π ∙ Гн/м. Для воздуха и других неферромагнитных материалов она незначительно отличается от магнитной проницаемости вакуума и при технических расчетах принимается равной 4π ∙ Гн/м. Так как абсолютная магнитная проницаемость для вакуума и указанных ранее материалов практически одинакова, то называется магнитной постоянной
. Абсолютная магнитная проницаемость ца ферромагнитных материалов непостоянна и во много раз превышает магнитную проницаемость вакуума. Число, показывающее, во сколько раз абсолютная магнитная проницаемость ферромагнитного материала больше магнитной постоянной , называется
относительной магнитной проницаемостью
, или (сокращенно) магнитной проницаемостью:
.
· Магнитные свойства вещества
Постоянные магниты могут быть изготовлены лишь из сравнительно немногих веществ, но все вещества, помещенные в магнитное поле, намагничиваются, т. е. сами становятся источниками магнитного поля. В результате этого вектор магнитной индукции при наличии вещества отличается от вектора магнитной индукции в вакууме.
Определение
Магнитная проницаемость вещества
μ показывает, во сколько раз вектор магнитной индукции в веществе больше, чем вектор магнитной индукции в вакууме, то есть
=μ⋅
Магнитные свойства вещества определяют по тому, как эти вещества реагируют на внешнее магнитное поле и каким образом упорядочена их внутренняя структура. Существует три основных класса веществ с резко различающимися магнитными свойствами: ферромагнетики, парамагнетики и диамагнетики.
Вещества, у которых, подобно железу, μ≫1, называются ферромагнетиками
.
Важнейшее свойство ферромагнетиков − существование у них остаточного магнетизма. Из ферромагнетиков изготавливают постоянные магниты.
Однако при нагревании до достаточно высокой температуры ферромагнитные свойства у тел исчезают (точка Кюри).
Температура, при которой вещество теряет ферромагнитные свойства, называется температурой или точкой Кюри
.
| Железо (Fe) | 77 С |
| Никель (Ni) | 36 С |
| Кобальт (Co) | 100 С |
При нагревании постоянного магнита выше этой температуры он перестает притягивать железные предметы. Магнитная проницаемость ферромагнетиков непостоянна, она зависит от магнитной индукции внешнего поля.
Существуют вещества, которые ведут себя подобно железу, т.е. втягиваются в магнитное поле. Эти вещества называют парамагнитными
. У них μ>1, но от единицы отличается на величину порядка .
Магнитная проницаемость парамагнетиков зависит от температуры и уменьшается при ее увеличении. Без намагничивающего поля парамагнетики не создают собственного магнитного поля. Постоянных парамагнетиков нет.
Диамагнетики
— вещества, которые выталкиваются из магнитного поля. У диамагнетиков μ<1, отличается от единицы на величину порядка .
Магнитная проницаемость практически не зависит от индукции намагничивающего поля и от температуры. При вынесении диамагнетика из внешнего намагничивающего поля он полностью размагничивается и магнитного поля не создает.
Сверхпроводники − идеальные диамагнетики. Магнитное поле вообще не проникает внутрь сверхпроводника. Это означает, что сверхпроводник является идеальным диамагнетиком. Так как магнитная индукция внутри проводника равна нулю, то по формуле =μ⋅ магнитная проницаемость μ сверхпроводника также равна нулю.
· Намагничивание ферромагнетика. Этапы намагничивания.
Намагничивание ферромагнетиков представляет собой процесс, состоящий из нескольких этапов.
На первом этапе при увеличении напряжённости внешнего магнитного поля увеличиваются размеры тех доменов, у которых собственный магнитный момент образует с внешним полем острый угол. При этом уменьшается объём тех доменов, у которых этот угол тупой.
______________________________
* Обычно размеры домена составляют 10-4…10-5 м.
К концу первого этапа домены, у которых упомянутый угол острый, полностью поглощают те, у которых угол между собственным и внешним магнитным полем тупой.
Этот этап намагничивания называют этапом смещения границ.
На втором этапе дальнейшее увеличение напряжённости внешнего магнитного поля вызывает поворот магнитных моментов доменов в сторону внешнего магнитного поля.
Второй этап намагничивания называют этапом вращения.
К концу второго этапа магнитные моменты всех доменов направлены по внешнему магнит-ному полю. По окончании этого этапа наступает третий этап намагничивания – этап насыщения.
В ходе первого и второго этапов намагничивания поле внутри ферромагнетика растёт за счёт увеличения как внешнего магнитного поля, так и магнитного поля, созданного доменами.
На третьем этапе увеличение магнитного поля в ферромагнетике происходит только за счёт роста внешнего магнитного поля. Суммарное магнитное поле доменов не изменяется.
· Явление гистерезиса
Если уменьшать магнитное поле, которое вызвало намагничивание ферромагнетика, то окажется, что зависимость индукции магнитного поля в ферромагнетике от напряжённости внешнего магнитного поля не совпадает с начальной кривой намагничивания.
При уменьшении напряжённости внешнего магнитного поля до нуля, магнитное поле в ферромагнетике не уменьшится до нуля. Индукция магнитного поля в ферромагнетике окажется равной В
ост – остаточной индукции поля в ферромагнетике. Другими словами – образец ферромагнетика после выключения внешнего магнитного поля останется намагниченным.
Для того, чтобы уменьшить индукцию магнитного поля в ферромагнетике до нуля, необходимо изменить направление внешнего магнитного поля на противоположное и начать постепенное увеличение его напряжённости.
При некоторой напряжённости Н
с индукция поля в ферромагнетике уменьшится до нуля. Эту напряжённость принято называть
коэрцитивной силой
.
Дальнейшее увеличение напряжённости вызывает намагничивание ферромагнетика. Направление намагничивания противоположно первоначальному.
Если после намагничивания до насыщения вновь уменьшать напряжённость внешнего магнитного поля, то процесс пойдёт так, как показано на рисунке.
График зависимости В
(
Н
) замкнётся, образовав так называемую
петлю гистерезиса
. Само рассматриваемое явление называется
явлением гистерезиса.
Явление гистерезиса заключается в том, что значение В
при данном
Н
зависит от того, какое значение
Н
имела ранее. Например, если ферромагнетик не намагничен, то при
Н
= 0
В
= 0.
Если ферромагнетик ранее находился в магнитном поле с Н
>0, то при
Н
= 0
В
=
В
ост
Если же ранее напряжённость была отрицательной, то при Н
= 0
В
=-
В
ост
Ферромагнетики делят на две группы. Основанием для классификации является коэрцитивная сила.
Коэрцитивная сила показывает, насколько трудно размагнитить ферромагнетик. Если коэрцитивная сила велика, то ферромагнетик размагнитить трудно. Такие ферромагнетики называют магнитожёсткими
. Из жёстких ферромагнетиков изготавливают постоянные магниты.
Если коэрцитивная сила мала, ферромагнетик можно размагнитить, почти не затрачивая на это энергию. Такие ферромагнетики называют магнитомягкими.
Из них изготавливают сердечники трансформаторов.
Контрольные вопросы
1. Может ли существовать магнитное поле независимо от электрического поля?
2. Каким правилом определяются направления силовых магнитных линий?
3. В каких единицах измеряется магнитная индукция?
4. От каких параметров зависит магнитная индукция
4. Что называется относительной магнитной проницаемостью ц?
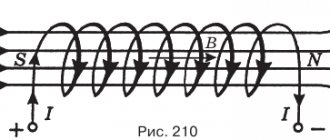
Контур с током и катушка индуктивности
Контур с током может быть одиночным (одновитковая катушка)
Контур с током может состоять из нескольких контуров (многовитковая катушка)
В электротехнике и радиотехнике применяются многовитковые катушки.
Чем больше витков, тем больше индуктивность катушки. Один и тот же ток, протекающий через одиночный виток и через многовитковую катушку, создаст разное по силе магнитное поле. У многовитковой катушки индуктивность больше, чем у одного витка; она пропорциональна количеству витков.
Когда нужно создать сильное магнитное поле, наматывают сотни и тысячи витков из тонкой медной проволоки. Такие катушки применяются в электромагнитах, трансформаторах, электродвигателях.
Индуктивность, индукция, самоиндукция
Если обозначение индуктивности L выбрано в честь физика Ленца, то единица измерения индуктивности Генри (Гн) носит имя другого физика – Джозефа Генри.
Ленц исследовал магнитные явления, возникающие при наличии постоянного тока, а Генри занимался переменным током. Точнее, он рассматривал переходные процессы, возникающие при включении и выключении электрического тока.
Что происходит, когда ток в цепи, содержащей катушку индуктивности, включается? Он не возрастает мгновенно, а увеличивается плавно. Чем больше витков в катушке, тем более растянут во времени процесс нарастания тока. Но число витков влияет еще и на силу магнитного поля, создаваемого током в катушке!
Джозеф Генри установил связь этих явлений. Оказывается, чем больше индуктивность, тем более инерционный процесс возрастания тока при включении. Это можно сравнить с массой в механике: чем массивнее тело, тем дольше оно разгоняется при воздействии на него силы.
Почему в катушке тормозится увеличение тока? Мы наблюдаем здесь явление самоиндукции. Ведь ток создает магнитное поле, не так ли?
Но на этом преобразование полей не останавливается. Меняющееся магнитное поле создает электрическое поле! Если в поле находится проводник, в нем наводится электродвижущая сила. Это явление названо электромагнитной индукцией.
Именно меняющееся, переменное магнитное поле способно создать электрическое поле и навести в проводнике электрический ток.
После того, как щелкнул выключатель, в цепи происходят такие процессы:
- Появляется и начинает увеличиваться электрический ток;
- Возрастающий электрический ток создает меняющееся магнитное поле;
- Переменное магнитное поле в том же самом проводнике наводит электрическое напряжение, противоположное приложенному;
- Наведенная магнитным полем электродвижущая сила, противоположная напряжению от источника, уменьшает суммарное напряжение, действующее на цепь, а ток соответствует уменьшенному напряжению.
Напряжение, наведенное магнитным полем в проводнике, называется ЭДС самоиндукции. Ток в проводнике является причиной возникновения противоположного напряжения в том же проводнике, то есть причиной торможения тока является сам ток; поэтому процесс назван самоиндукцией.
Величина ЭДС самоиндукции зависит от скорости изменения тока и от индуктивности:
Минус в формуле указывает на то, что в цепи возникает противо ЭДС, направленная так, чтобы тормозить изменение тока.
В соответствии с этой формулой, единицу индуктивности 1 Генри определили следующим образом:
Один Генри – это индуктивность, при которой скорость изменения тока, равная одному амперу в секунду, приводит к наведению ЭДС самоиндукции, равной одному вольту.
1Вольт = — 1 Генри * 1 Ампер/секунда, или
1В = — 1 Гн * 1А/с
Индуктивность как мера самоиндукции проще поддается измерению, чем индуктивность – как коэффициент между током и магнитным потоком. В благодарность за открытие явления самоиндукции физики присвоили имя Джозефа Генри единице измерения индуктивности.
Ёмкость плоского конденсатора
Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.
Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.
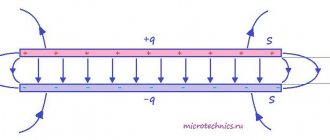
Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.
Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух
Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.
Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.
Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:
Здесь — напряжённость поля положительной обкладки, — напряженность поля отрицательной обкладки, — поверхностная плотность зарядов на обкладке:
На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.
Рис. 1. Электрическое поле плоского конденсатора
Согласно принципу суперпозиции, для результирующего поля имеем:
Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):
Внутри конденсатора поле удваивается:
или
(4)
Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:
Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.
Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.
Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):
(5)
Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:
(6)
Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.
Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:
(7)
Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними. Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?
Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:
(8)
Соответственно, напряжение на конденсаторе:
(9)
Отсюда ёмкость плоского конденсатора с диэлектриком:
(10)
Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.
Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.
Энергия магнитного поля
Магнитное поле обладает энергией. Магнитные силы совершают механическую работу, притягивая или отталкивая другие магниты или тела из магнитных материалов. Меняющееся магнитное поле индуцирует электрический ток в проводниках.
Магнитную энергию можно выразить через математическую формулу. В предыдущем разделе упоминалась инерционность индуктивной цепи, ее роль в электромагнитных явлениях сравнивалась с ролью массы в механике. Интересно, что эта аналогия углубляется при рассмотрении энергии.
Формула энергии магнитного поля похожа на формулу кинетической энергии механического тела:
Энергия магнитного поля пропорциональна индуктивности и квадрату величины тока.
Во время переходного процесса, когда при включении ток в цепи замедленно нарастает, происходит накопление магнитной энергии. Эта энергия может использоваться для совершения работы. И эта энергия создает проблемы при выключении тока в цепи с большой индуктивностью.
Если ток уменьшать, возникнет ЭДС, замедляющая уменьшение тока. Но если ток выключить, резко разорвав цепь, скорость изменения тока от конкретного значения до нуля теоретически должна быть бесконечно велика. Это значит, ЭДС самоиндукции при выключении тока тоже должна быть бесконечно велика.
Этот математический парадокс возник из-за упрощенных идеализированных формул. В реальности ток не прекращается мгновенно, размыкание контактов занимает некоторый короткий промежуток времени, но все равно скорость изменения тока велика, и наводится ЭДС значительной величины. Обычным явлением при выключении цепи является искрение. Если выключать ток в цепи с большой индуктивностью, то попытка резкого прекращения тока может стать причиной вспышки электрической дуги.
Что произойдет, если дуга не вспыхнула, а ток прекратился? Куда девалась энергия магнитного поля? Частично она перешла в тепловую энергию – контакты выключателя нагрелись. Остальная часть энергии магнитного поля, при его резком уменьшении до нуля, перешла в электромагнитную волну. Переменное магнитное поле индуцировало переменное электрическое поле; в свою очередь, переменное электрическое вызвало новую волну магнитного, и так далее.
Выключение тока простым щелчком выключателя – посылает в бесконечное пространство широкий «шумовой» спектр электромагнитных колебаний.
Энергия электрического поля
При зарядке конденсатора энергия запасается в виде энергии электрического поля и может быть возвращена источнику при преобразовании в другой вид энергии.
Выражение энергии через характеристики конденсатора
Заряд конденсатора образуется переносом заряженных частиц с одной обкладки на другую под действием внешнего источника энергии. Работа, совершенная при переносе единицы заряда, численно равна напряжению между обкладками. Если бы напряжение в процессе зарядки не изменялось, то энергию можно было бы определить произведением напряжения и заряда [см. формулу (1.5)]. Однако в процессе накопления заряда растет и напряжение, поэтому при определении энергии, затраченной на образование заряда, нужно учесть зависимость между напряжением и зарядом (7.28). Если емкость конденсатора — величина постоянная, зависимость между напряжением и зарядом графически выражается прямой линией (рис. 11.1).
Рис. 11.1. К определению энергии электрического поля
Предположим, что заряд Q1 увеличился на dQ — величину столь малую, что в пределах изменения заряда напряжение можно считать неизменным:
Выражение энергии через характеристики электрического поля
Выражение (11.2) получено на основе закона сохранения энергии; однако из него непосредственно не следует, что энергия Wэ является энергией электрического поля. Можно показать, что эта энергия распределена в электрическом поле. Для примера рассмотрим равномерное электрическое поле плоского конденсатора (см. рис. 1.6, а).
Поток вектора электрического смещения через любую поверхность, проведенную в диэлектрике параллельно пластинам, равен заряду Q конденсатора, что следует из формулы (7.33): DS = Q. Напряженность равномерного электрического поля Е = U/l. Следовательно, где V — объем диэлектрика, в котором распределено поле, связанное с заряженными пластинами конденсатора. Отношение энергии к объему диэлектрика дает объемную плотность энергии электрического поля: Энергия, определенная формулой (11.2) через характеристики проводников, выражена также формулой (11.5) через характеристики электрического поля. Эквивалентность этих формул свидетельствует о том, что энергия системы заряженных тел является энергией электрического поля.
Задача 11.1.
Плоский воздушный конденсатор емкостью 600 пФ при расстоянии между электродами 2 см заряжен до напряжения U = 4 кВ и отключен от источника напряжения. Определить изменение энергии и напряженности электрического поля конденсатора при уменьшении расстояния между электродами вдвое. Решение. До изменения расстояния между обкладками энергия электрического поля, по формуле (11.3), Напряженность электрического поля [см. (1.5)] При уменьшении расстояния между обкладками вдвое емкость конденсатора согласно формуле (7.29) увеличивается вдвое. При этом заряд конденсатора не изменяется (предполагается, что утечки заряда нет). Вследствие увеличения емкости конденсатора напряжение между обкладками уменьшится во столько же раз [см. формулу (7.28)]: Энергия электрического поля Напряженность электрического поля
Механические силы в электрическом поле
Вопрос о механических силах в электрическом поле рассмотрим на примере плоского конденсатора, заряженного от внешнего источника энергии, имеющего напряжение U. Электрическое поле конденсатора будем полагать равномерным.
Энергетический баланс в электростатической системе
Силы Fэ, возникающие вследствие взаимодействия пластин с электрическим полем, приложены к пластинам и направлены так, что они притягиваются. Предположим, что одна из пластин конденсатора свободна, и возможное малое перемещение ее под действием силы Fэ обозначим через dх (рис. 11.2). Рис. 11.2. Механические силы в электрическом поле
В дальнейших рассуждениях будем исходить из того, что при изменении заряда конденсатора не возникает потерь энергии в проводниках в связи с перемещением заряженных частиц и в диэлектрике вследствие изменения напряженности поля.
При таких условиях в соответствии с законом сохранения энергии при изменении заряда конденсатора на dQ за счет энергии внешнего источника изменяется энергия электрического поля на dWэ и совершается механическая работа Fэdx:
Обобщенное выражение электрической силы (первый случай)
Заряд конденсатора остается неизменным (Q = const), т. е. заряженный конденсатор отключен от внешнего источника энергии. При dQ = 0 работа внешнего источника UdQ = 0. Поэтому или Последнее равенство показывает, что механическая работа, связанная с перемещением пластины, совершается за счет энергии электрического поля. Действительно, механическая работа, совершаемая электрической силой, положительна (Fэdх > 0), следовательно, изменение энергии электрического поля отрицательно (dWэ
Механическую силу, стремящуюся изменить положение пластины конденсатора, можно выразить отношением Рассуждая аналогично, можно получить зависимость между механическим моментом и углом поворота α, если механическое движение осуществляется в виде вращения одной пластины по отношению к другой: Изменение расстояния l между пластинами на dх изменит емкость конденсатора. При уменьшении расстояния емкость увеличивается, а напряжение между пластинами уменьшается, что непосредственно следует из формулы (7.28).
Предположим, что расстояние между пластинами увеличивается благодаря действию на пластины внешних механических сил. Энергия в системе возрастает на величину работы, совершенной внешним источником механической энергии. При этом емкость конденсатора уменьшится, а напряжение между пластинами увеличится.
Обобщенное выражение электрической силы (второй случай)
Напряжение между пластинами остается постоянным (U = const), т. е. во время движения пластины конденсатор не отключается от внешнего источника энергии.
При уменьшении расстояния между пластинами увеличивается емкость конденсатора, что при неизменном напряжении влечет за собой увеличение заряда.
Внешний источник энергии должен затратить энергию на увеличение заряда конденсатора в количестве UdQ.
Изменение энергии электрического поля dWэ при изменении заряда, согласно формуле (11.2), , т. е. составляет половину энергии внешнего источника, израсходованной при увеличении заряда конденсатора. Вторая половина энергии расходуется на покрытие механической работы Fэdх, следовательно, Отсюда Аналогично, при вращательном движении
Увеличение расстояния между пластинами в результате действия внешних механических сил приведет к уменьшению емкости. Но при постоянном напряжении за уменьшением емкости последуют уменьшение заряда конденсатора и уменьшение энергии электрического поля. В этом случае механическая работа, связанная с перемещением пластины, совершается внешними механическими силами. Величина этой работы численно равна уменьшению энергии электрического поля. Таким образом, источнику электрической энергии возвращается энергия, численно равная удвоенному значению механической работы.
Распрямим провод — индуктивность остается
Первоначально индуктивность считали атрибутом контура или катушки. Причина этого – в способах измерения. Магнитный поток через контур или катушку локализован, его можно измерить (хотя точность измерений долгое время была невысокой). Если катушку раскрутить и провод выпрямить, и пропускать ток по прямому проводу, магнитное поле все равно возникнет. Но померить его поток непросто!
А что произойдет с самоиндукцией? Ток в прямом проводе возрастает быстрее, чем в катушке. Но если провод протянуть на несколько километров (построить линию электропередач), то явление самоиндукции наблюдается. Возрастание тока, при его подаче в линию передач, происходит не мгновенно. Значит, прямой провод обладает индуктивностью, хотя и меньшей, чем катушка.
На рисунке показан проводник с током и силовые линии магнитного поля, имеющие форму окружностей.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.
Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.
Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.
Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .
Возьмём на второй обкладке настолько маленькую площадку, что заряд этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
где — напряжённость поля первой обкладки:
Следовательно,
Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).
Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил , с которыми притягиваются к первой обкладке всевозможные маленькие заряды второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все и дадут . В результате получим:
(11)
Предположим теперь, что расстояние между обкладками изменилось от начальной величины до конечной величины . Сила притяжения пластин совершает при этом работу:
Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.
С учётом формул (11) и (7) имеем:
где
Это можно переписать следующим образом:
где
(12)
Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.
Используя соотношение , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):
(13)
(14)
Особенно полезными являются формулы (12) и (14).
Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:
При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).
Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
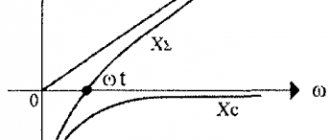
Индуктивность и реактивное сопротивление
Катушка индуктивности может оказывать ничтожно малое сопротивление установившемуся постоянному току, но ее сопротивление переменному току значительно. Такое сопротивление называется реактивным.
Реактивное сопротивление переводит энергию электрического тока в энергию электромагнитного поля. Если на цепь, обладающую индуктивностью L, подать переменное напряжение с частотой f, то реактивное сопротивление будет равно
Чем выше реактивное сопротивление, тем меньше будет переменный ток.
Реактивное сопротивление зависит от частоты. Элементы с маленькой индуктивностью создают ничтожно малое сопротивление на низких частотах, но при переходе от частоты 50 Герц к частоте 50 МГц (мегагерц) сопротивление возрастает в миллион раз.
При низких частотах не принимаются во внимание индуктивности небольших отрезков провода, но при сотнях мегагерц и при гигагерцах приходится учитывать даже индуктивность проволочных выводов радиодеталей. В технике сверхвысоких частот применяются безкорпусные элементы, не имеющие проволочных выводов. Вместо них – контактные площадки, которые паяют на печатную плату.
Цепь с индуктивным сопротивлением, при подаче переменного тока, излучает электромагнитные волны. Но возможен и обратный процесс: при воздействии электромагнитного поля в индуктивности наводится переменный ток.
Стиральная машина и индуктивное сопротивление
Пользователи автоматических стиральных машин часто жалуются на то, что ток «пробивает на барабан». Электрическая изоляция таких машин, как правило, в полном порядке, но все равно есть неприятное ощущение от прикосновения к металлическому барабану, при загрузке и выгрузке вещей.
Причина – в наведенном токе. Машина-автомат имеет блок питания, в котором сетевое напряжение преобразуется в высокочастотное. Это высокочастотное напряжение наводится на все электропроводящие предметы, в частности на металлический барабан. Индуктивность барабана не нормируется, но наверняка она мала. Тем не менее, ток высокой частоты электронной схемы индуцирует на металлических частях стиральной машины отклик – небольшой ток.
Подобное явление иногда наблюдают пользователи современных водонагревателей с электронным управлением, греющих водопроводную воду. Если блок питания в устройстве оказывается близко к трубе с водой, на ней может наводиться переменный высокочастотный ток, и вода из крана «щиплется». Избежать неприятных ощущений можно, отключив электрическое напряжение от котла.
Индуктивность человеческого тела
Наше тело является электрическим проводником, а все проводники, в той или иной степени, обладают индуктивностью. Это значит, что мы подвержены воздействию электромагнитного поля, под его воздействием в нашем теле могут индуцироваться переменные токи.
Индуктивность человеческого тела значительно меньше. чем индуктивность антенны или дросселя, и небольшие электромагнитные поля практически не влияют на нас. Но чем выше мощность излучения, а главное – чем выше частота электромагнитного поля, тем воздействие сильнее. Сильное поле СВЧ диапазона представляет смертельную опасность.
Для защиты людей на производствах, связанных с сильными электромагнитными полями, применяют специальную экранирующую одежду, экранированные помещения. Существуют зоны, закрытые для посещения – вокруг мощных антенн, радиолокаторов.
Периодически появляется информация о вреде длительных разговоров по мобильному телефону, когда трубка прижата к голове. Телефон излучает высокочастотный электромагнитный сигнал небольшой мощности, из-за малой мощности его влияние незначительно. Но при длительном воздействии это излучение может нанести вред здоровью. Использовать скайп, установленный на компьютер, предпочтительнее.