Теория
Электромагнитное поле – аналог механической силы, проявляется воздействием на перемещающиеся носители электрического заряда, тела с магнитным моментом. Характеризуется механической силой, которое поле оказывает на проводники либо магниты.
Опыты показывают, что магнитное поле пытается сориентировать магнитную стрелку, развернуть её относительно плоскости витка, в направлении, которое называется направлением поля. Для планеты его принимают за линию, направленную с географического севера на юг. Электрическое поле характеризуется векторной величиной E – напряженностью. Для описания магнитного воздействия применяют величину B, названную магнитной индукцией.
Во избежание путаницы характеристики носят разные названия.
Направлением B считают то, куда укажет магнитная стрелка относительно витка с электрическим током. Его модуль определяют по максимальному значению вращающего момента Mmax, действующего на стрелку. При одинаковом значении индукции в каждой точке пространства поле называется однородным, когда его величина проявляется в веществе в разной степени – неоднородным.
§16. Магнитное поле и его характеристики и свойства
Магнитное поле и его характеристики.
При прохождении электрического тока по проводнику вокруг него образуется магнитное поле. Магнитное поле представляет собой один из видов материи. Оно обладает энергией, которая проявляет себя в виде электромагнитных сил, действующих на отдельные движущиеся электрические заряды (электроны и ионы) и на их потоки, т. е. электрический ток. Под влиянием электромагнитных сил движущиеся заряженные частицы отклоняются от своего первоначального пути в направлении, перпендикулярном полю (рис. 34).
Рис. 34. Схемы действия магнитного поля на движущиеся электрические заряды: положительный ион (а) и электрон (б).
Магнитное поле образуется только вокруг движущихся электрических зарядов, и его действие распространяется тоже лишь на движущиеся заряды. Магнитное и электрические поля неразрывны и образуют совместно единое электромагнитное поле. Всякое изменение электрического поля приводит к появлению магнитного поля и, наоборот, всякое изменение магнитного поля сопровождается возникновением электрического поля. Электромагнитное поле распространяется со скоростью света, т. е. 300 000 км/с.
Графическое изображение магнитного поля.
Графически магнитное поле изображают магнитными силовыми линиями, которые проводят так, чтобы направление силовой линии в каждой точке поля совпадало с направлением сил поля; магнитные силовые линии всегда являются непрерывными и замкнутыми. Направление магнитного поля в каждой точке может быть определено при помощи магнитной стрелки.
Северный полюс стрелки всегда устанавливается в направлении действия сил поля. Конец постоянного магнита, из которого выходят силовые линии (рис. 35, а), принято считать северным полюсом, а противоположный конец, в который входят силовые линии,— южным полюсом (силовые линии, проходящие внутри магнита, не показаны).
Распределение силовых линий между полюсами плоского магнита можно обнаружить при помощи стальных опилок, насыпанных на лист бумаги, положенный на полюсы (рис. 35, б).
Рис. 35. Магнитное поле, созданное постоянным магнитом.
Для магнитного поля в воздушном зазоре между двумя параллельно расположенными разноименными полюсами постоянного магнита характерно равномерное распределение силовых магнитных линий (рис. 36) (силовые линии, проходящие внутри магнита, не показаны).
Рис. 36. Однородное магнитное поле между полюсами постоянного магнита.
Для более наглядного изображения магнитного поля силовые линии располагают реже или гуще. В тех местах, где магнитное роле сильнее, силовые линии располагают ближе друг к другу, там же, где оно слабее,— дальше друг от друга. Силовые линии нигде не пересекаются.
Во многих случаях удобно рассматривать магнитные силовые линии как некоторые упругие растянутые нити, которые стремятся сократиться, а также взаимно отталкиваются друг от друга (имеют взаимный боковой распор). Такое механическое представление о силовых линиях позволяет наглядно объяснить возникновение электромагнитных сил при взаимодействии магнитного поля и Проводника с током, а также двух магнитных полей.
Основными характеристиками магнитного поля являются магнитная индукция, магнитный поток, магнитная проницаемость и напряженность магнитного поля.
Магнитная индукция и магнитный поток.
Интенсивность магнитного поля, т. е.способность его производить работу, определяется величиной, называемой магнитной индукцией. Чем сильнее магнитноe поле, созданное постоянным магнитом или электромагнитом, тем большую индукцию оно имеет. Магнитную индукцию В можно характеризовать плотностью силовых магнитных линий, т. е. числом силовых линий, проходящих через площадь 1 м2 или 1 см2, расположенную перпендикулярно магнитному полю.
Различают однородные и неоднородные магнитные поля. В однородном магнитном поле магнитная индукция в каждой точке поля имеет одинаковое значение и направление. Однородным может считаться поле в воздушном зазоре между разноименными полюсами магнита или электромагнита (см.рис.36) при некотором удалении от его краев. Магнитный поток Ф, проходящий через какую-либо поверхность, определяется общим числом магнитных силовых линий, пронизывающих эту поверхность, например катушку 1 (рис. 37, а), следовательно, в однородном магнитном поле
Ф = BS (40)
где S — площадь поперечного сечения поверхности, через которую проходят магнитные силовые линии. Отсюда следует, что в таком поле магнитная индукция равна потоку, поделенному на площадь S поперечного сечения:
B = Ф/S (41)
Если какая-либо поверхность расположена наклонно по отношению к направлению магнитных силовых линий (рис. 37, б), то пронизывающий ее поток будет меньше, чем при перпендикулярном ее положении, т. е. Ф2 будет меньше Ф1.
В системе единиц СИ магнитный поток измеряется в веберах (Вб), эта единица имеет размерность В*с (вольт-секунда). Магнитная индукция в системе единиц СИ измеряется в теслах (Тл); 1 Тл = 1 Вб/м2.
Рис. 37. Магнитный поток, пронизывающий катушку при перпендикулярном (а) и наклонном (б) ее положениях по отношению к направлению магнитных силовых линий.
Магнитная проницаемость.
Магнитная индукция зависит не только от силы тока, проходящего по прямолинейному проводнику или катушке, но и от свойств среды, в которой создается магнитное поле. Величиной, характеризующей магнитные свойства среды, служит абсолютная магнитная проницаемость а. Единицей ее измерения является генри на метр (1 Гн/м = 1 Ом*с/м).
В среде с большей магнитной проницаемостью электрический ток определенной силы создает магнитное поле с большей индукцией. Установлено, что магнитная проницаемость воздуха и всех веществ, за исключением ферромагнитных материалов (см. § 18), имеет примерно то же значение, – что и магнитная проницаемость вакуума.
Абсолютную магнитную проницаемость вакуума называют магнитной постоянной,
μa = 4π*10-7 Гн/м.
Магнитная проницаемость ферромагнитных материалов в тысячи и даже десятки тысяч раз больше магнитной проницаемости неферромагнитных веществ. Отношение магнитной проницаемости μа какого-либо вещества к магнитной проницаемости вакуума μо называют относительной магнитной проницаемостью:
μ = μа/μо (42)
Напряженность магнитного поля. Напряженность И не зависит от магнитных свойств среды, но учитывает влияние силы тока и формы проводников на интенсивность магнитного поля в данной точке пространства. Магнитная индукция и напряженность связаны отношением
H = B/μа = B/(μ*μо) (43)
Следовательно, в среде с неизменной магнитной проницаемостью индукция магнитного поля пропорциональна его напряженности. Напряженность магнитного поля измеряется в амперах на метр (А/м) или амперах на сантиметр (А/см).
Физический смысл магнитной индукции
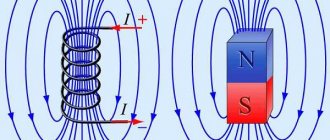
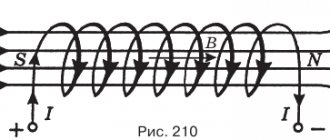
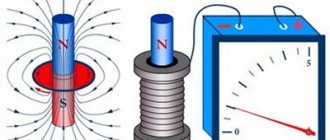
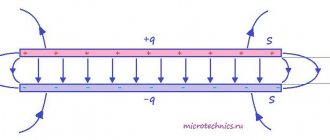
Прежде, чем перейти к рассмотрению формулы магнитной индукции, нужно выяснить, чем объясняется возникновение самого явления в системе. Соленоид не является плоским элементом и включает в себя спираль из проводника (металла). При отсутствии воздействующих на него магнитных явлений находящиеся в кристаллической решетке материала спирали электрозаряды ведут себя статично. Когда в соленоиде движется постоянный магнитный элемент, формирующий поле, под его влиянием движутся и заряженные частицы, тогда в индуктивном элементе появляется электрический ток, сила которого определяется характеристиками магнитного и спирального элемента и тем, как быстро происходит движение.
Важно! Имеющие одинаковую ориентацию поля суммируются, образуя общее поле. Когда передвижение заряженных частиц в соленоиде прекращается, сердечник перестает проявлять магнитные характеристики, если он выполнен из мягкого металла (к стальным изделиям это правило не относится).
Сила Лоренца
Когда некоторый участок провода, по которому идет электроток, находится в полевом пространстве, на движущиеся заряды действует сила со стороны поля. Ее называют силой Лоренца, по фамилии впервые обнаружившего это явление ученого. На ее значение оказывают влияние величины тока, индукции и угла между векторами этих двух величин.
Важно! Максимальное значение Лоренцовой силы достигается, когда проводниковый элемент образует с полем прямой угол. Когда направления поля и тока параллельны друг другу, рассматриваемая сила отсутствует.
Чтобы узнать вектор этой силы, можно воспользоваться правилом правой руки. Указательный палец нужно жестко зафиксировать в положении, показывающем вектор МП, а большой – отвести в сторону движения тока. В такой позиции средний палец при оттягивании под прямым углом к руке укажет в сторону приложения силы Лоренца.
Направление Лоренцовой силы
Для расчета значения этой величины для некоторого заряда, перемещающегося перпендикулярно полю, используют выражение:
F=B*q*v (здесь v – скорость движения заряда).
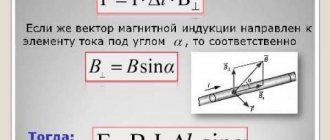
Когда имеется угол между направлениями, формула принимает вид:
F=B*q*v*sin α.
Если надо рассчитать индукцию в контуре, помещенном в однородное поле, используют равенство:
В=М(S*I),
где М – момент амперовой силы, а S – площадь поверхности контурного элемента.
Взаимосвязь напряженности МП и магнитной индукции
Общий вид формулы напряженности магнитного поля:
Н = I/(2*π*r).
Здесь Н – рассчитываемая величина, I – протекающий ток, r – дистанция до точки, чью характеристику поля надо оценить. Единица измерения напряженности выглядит как частное единиц, в которых измеряются сила тока и расстояние: ампера и метра (А/м).
Для соленоида, содержащего n витков и имеющего длину L, будет применяться выражение:
Н = I*n/L.
В условиях вакуума отношение величин напряженности и индукции может быть описано так:
В = μ0*Н,
где μ0 – константа, равная 1, 256*10-6.
С некоторым огрублением такое отношение справедливо и для воздушной среды. Когда в полевой зоне находится какой-то предмет, нужно учитывать магнитную проницаемость вещества, из которого он изготовлен (μ). Тогда отношение величин принимает следующий вид:
В= μ* μ0*Н.
У парамагнетиков (например, алюминиевых изделий) и особенно у ферромагнетиков (все виды железа и стали) значение μ велико, что ведет к возрастанию индукции, тогда как у диамагнитных изделий (например, медных) она меньше единицы, что несколько понижает плотность потока.
Опираясь на приведенные выражения, можно составить формулы для проводниковых изделий различной формы:
- для кольца с радиусом R: B=(μ*μ0*I*n)/2R;
- для прямого кабеля бесконечной протяженности: В=(I*n*μ*μ0)/(2π х r);
- для спирали: В=(I*n*μ*μ0)/L.
Применение силы Лоренца
Данное явление используется в датчиках, применяемых для непрямого замера электротока в локаторах, кабелях, выявления скорости транспорта или турбины. Масс-спектрометры, работая с данной силой, вычисляют удельные заряды элементарных частиц. Лоренцово воздействие заставляет заряды двигаться по кругу. Замерив радиус траектории движения, можно вычислить удельную величину, представляющую собой отношение заряда к массе. Выглядит выражение так:
Q/m=v/(B*r).
Масс-спектрометр
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm / I * ∆L, может быть найден с помощью других математических расчетов.
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока на поверхности, ограниченной кольцом.
Математически это можно описать формулой:
| Закон Фарадея Ɛi – индукционная ЭДС В ΔФ / Δt – скорость изменения магнитного потока Вт / с |
Знак «-» в формуле позволяет учитывать направление индукционного тока. Индукционный ток в замкнутой цепи всегда направлен так, что магнитный поток поля, создаваемого этим током через поверхность, ограниченную кольцом, уменьшает те изменения поля, которые вызывают появление индукционного тока.
Если цепь состоит из N витков (т.е это катушка), ЭДС индукции будет рассчитываться следующим образом.
| Закон Фарадея для цепи из N витков Ɛi – индукционная ЭДС В ΔФ / Δt – скорость изменения магнитного потока Вт / с N – количество оборотов |
Сила индукционного тока в замкнутом токопроводящем контуре с сопротивлением R:
| Закон Ома для проводящей цепи Ɛi – индукционная ЭДС В I – сила индукционного тока [А] R – сопротивление цепи [Ом] |
Если проводник длины l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B, ЭДС электромагнитной индукции будет равна:
| Индукционная ЭДС для движущегося проводника Ɛi – индукционная ЭДС В B – магнитная индукция [Тл] v – скорость проводника [м / с] l – длина жилы [м] |
Возникновение индукционного электромагнитного поля в проводнике, движущемся в магнитном поле, объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. В этом случае сила Лоренца играет роль внешней силы.
Проводник, движущийся в магнитном поле, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество тепла в цепи выделяется как за счет работы внешней силы, которая сохраняет скорость проводника неизменной, так и за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, попадающего в замкнутый контур, может происходить по двум причинам:
- из-за движения цепи или ее частей в постоянном магнитном поле с течением времени. Это тот случай, когда проводники, а вместе с ними и носители свободного заряда движутся в магнитном поле
- из-за изменения во времени магнитного поля с неподвижным контуром. В этом случае возникновение индукционной ЭДС уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Следовательно, явления индукции в подвижных и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока в этих двух случаях оказывается различной:
- в случае движущихся проводников ЭДС индукции возникает из-за силы Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия вихревого электрического поля на свободные заряды, возникающего при изменении магнитного поля.
Закон Био-Савара-Лапласа
Формула индукции ЭДС
Описывает правила поиска B → магнитного поля, которое создает постоянный электрический ток. Это экспериментально установленная модель. Био и Савар в 1820 году показали это на практике, Лаплас смог его сформулировать. Этот закон является фундаментальным в магнитостатике. На практике рассматривался фиксированный провод малого сечения, по которому пропускался электрический ток. Для исследования был выбран небольшой участок проволоки, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил также рассматривать движение электрона как ток и на этом утверждении с помощью этого закона доказал возможность определения МП наступающего точечного заряда.
Согласно этому физическому правилу каждый сегмент dl проводника, по которому протекает электрический ток I, образует магнитное поле dB в пространстве вокруг себя с интервалом r и под углом α:
дБ = µ0 * I * dl * sin α / 4 * π * r2,
где это находится:
- дБ – магнитная индукция, Тл;
- µ0 = 4 π * 10-7 – магнитная постоянная, Гн / м;
- I – сила тока, А;
- dl – отрезок жилы, м;
- r – расстояние от точки, где находится магнитная индукция, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП требуемого тока. Он будет равен векторной сумме.
Закон Био-Савара-Лапласа
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого движения электронов;
- поля кругового движения заряженных частиц.
Формула депутата первого рода:
В = µ * µ0 * 2 * I / 4 * π * r.
Для кругового движения это выглядит так:
В = µ * µ0 * I / 4 * π * r.
В этих формулах µ – (относительная) магнитная проницаемость среды).
Рассматриваемый закон следует из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, когда электрическое поле постоянно, только что рассматривали Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому полный вектор магнитной индукции в определенной точке равен векторной сумме всех векторов MI, созданных разными токами в данной точке:
B → = B1 → + B2 → + B3 →… + Bn→
Правило Ленца
Для определения направления индукционного тока необходимо использовать правило Ленца.
С академической точки зрения это правило звучит так: индукционный ток, возбуждаемый в замкнутой цепи при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле предотвращает изменение магнитного потока, вызывая индукционный ток.
Попробуем немного попроще: катушка в данном случае – недовольная бабушка. Они забирают магнитный поток: она несчастна и создает магнитное поле, которое этот магнитный поток хочет восстановить.
Они дают ей магнитный поток, они принимают его, они говорят, они используют его, и она такая – “Потому что ваш магнитный поток сдался мне!” и создает магнитное поле, которое вытесняет этот магнитный поток.
Единица измерения индукции
Единица индукции в системе СИ определяется как индукция такого магнитного поля, в котором на 1 м проводника при силе тока действует сила Ампера величиной 1 Н. Единица называется тесла (Тл).
$1 Тл = {1 Н\over {1 A*1 м}}$ (3).
Единица индукции названа в честь выдающегося сербского инженера, физика Николы Тесла (1856-1943 г.г.). Тесла изобрел электромеханические генераторы, высокочастотный трансформатор. Исследовал свойства токов высокой частоты, изобрел многофазный электродвигатель и системы передачи электроэнергии с помощью переменного тока. Тесла сформулировал основные принципы радиосвязи, изобрел мачтовую антенну для приемки и передачи радиосигналов.
Рис. 3. Портрет Никола Тесла.
Магнитный поток
Для характеристики воздействия индукционного фона на контур из металла используют такую величину, как поток. Она является скалярной. В контексте этого необходимо узнать, индукция в чем измеряется. Она зависит от количества идущих через единицу сечения проводящего элемента силовых линий. В международной системе СИ за измерительную единицу принимается Тесла (Тл). Отсюда и название устройства, предназначенного для замеров – теслометра. 1 Тл – индукция, возникающая в полевом пространстве, в котором момент силы в 1 Н*м оказывает воздействие на контур площадью 1 квадратный метр, по которому течет ток в 1 ампер.
Магнитный поток