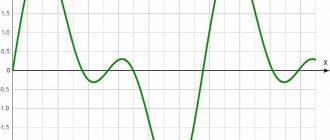
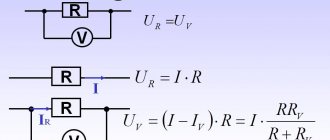Формы и характеристики электрических сигналов

Часто в электронных схемах требуется сгенерировать разные типы сигналов, имеющих различные частоты и формы, такие как меандры, прямоугольные, треугольные, пилообразные сигналы и различные импульсы.

Эти сигналы различной формы могут использоваться в качестве сигналов синхронизации, тактирующих сигналов или в качестве запускающих синхроимпульсов. В первую очередь необходимо понять основные характеристики, описывающие электрические сигналы.

С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени. То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени. Существует множество различных типов электрических сигналов, но в целом, все они могут быть разбиты на две основные группы.

Однополярные сигналы — это электрические сигналы, которые всегда положительные или всегда отрицательные, не пересекающие горизонтальную ось. К однонаправленным сигналам относятся меандр, тактовые импульсы и запускающие импульсы.
Двухполярные сигналы — эти электрические сигналы также называют чередующимися сигналами, так как они чередуют положительные значения с отрицательными, постоянно пересекая нулевое значение. Двухполярные сигналы имеют периодическое изменение знака своей амплитуды. Наиболее распространенным из двунаправленных сигналов, является синусоидальный.

Будучи однонаправленными, двунаправленными, симметричными, несимметричными, простыми или сложными, все электрические сигналы имеют три общие характеристики:

Период — это отрезок времени, через который сигнал начинает повторяться. Это временное значение также называют временем периода для синусоид или шириной импульса для меандров и обозначают буквой T.
Частота — это число раз, которое сигнал повторяет сам себя за период времени равный 1 секунде. Частота является величиной, обратной периоду времени, ( *** QuickLaTeX cannot compile formula: f = 1/T *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37 ). Единицей измерения частоты является Герц (Гц). Частотой в 1Гц, обладает сигнал, повторяющий 1 раз за 1 cекунду.
Амплитуда — это величина изменения сигнала. Измеряется в Вольтах (В) или Амперах (А), в зависимости от того, какую временную зависимость (напряжения или тока) мы используем.

Периодические сигналы

Периодические сигналы являются самыми распространенными, поскольку включают в себя синусоиды. Переменный ток в розетке дома представляет из себя синусоиду, плавно изменяющуюся с течением времени с частотой 50Гц.

Время, которое проходит между отдельными повторениями цикла синусоиды называется ее периодом. Другими словами, это время, необходимое для того, чтобы сигнал начал повторяться.

Период может изменяться от долей секунды до тысяч секунд, так как он связан с его частотой. Например, синусоидальный сигнал, которому требуется 1 секунда для совершения полного цикла, имеет период равный одной секунде. Аналогично, для синусоидального сигнала, которому требуется 5 секунд для совершения полного цикла, имеет период равный 5 секундам, и так далее.

Итак, отрезок времени, который требуется для сигнала, чтобы завершить полный цикл своего изменения, прежде чем он вновь повторится, называется периодом сигнала и измеряется в секундах. Мы можем выразить сигнал в виде числа периодов T в секунду, как показано на рисунке ниже.

Ссылки

[standartgost.ru/%D0%93%D0%9E%D0%A1%D0%A2%2016465-70 ГОСТ 16465-70].

Это заготовка статьи об электронике. Вы можете помочь проекту, дополнив её.

: неверное или отсутствующее изображение

Для улучшения этой статьи желательно:

Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).К:Википедия:Страницы на КУЛ (тип: не указан)
Найти и оформить в виде сносок ссылки на независимые авторитетные источники, подтверждающие написанное.К:Википедия:Статьи без источников (тип: не указан)

Синусоидальный сигнал

Время периода часто измеряется в секундах ( с ), миллисекундах (мс) и микросекундах (мкс).

Для синусоидальной формы волны, время периода сигнала также можно выражать в градусах, либо в радианах, учитывая, что один полный цикл равен 360° (Т = 360°), или, если в радианах, то

*** QuickLaTeX cannot compile formula: 2 \pi *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37 (T = *** QuickLaTeX cannot compile formula: 2 \pi *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37

Период и частота математически являются обратными друг другу величинами. С уменьшением времени периода сигнала, его частота увеличивается и наоборот.

Соотношения между периодом сигнала и его частотой:

*** QuickLaTeX cannot compile formula: f = \frac{1}{T} *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37

Гц

*** QuickLaTeX cannot compile formula: T = \frac{1}{f} *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37

Один герц в точности равен одному циклу в секунду, но один герц является очень маленькой величиной, поэтому часто можно встретить префиксы, обозначающие порядок величины сигнала, такие как кГц, МГц, ГГц и даже ТГц

Префикс	Определение	Запись	Период
Кило	тысяча	кГц	1 мс
Мега	миллион	МГц	1 мкс
Гига	миллиард	ГГц	1 нс
Тера	триллион	ТГц	1 пс

Меандр

Меандры широко используются в электронных схемах для тактирования и сигналов синхронизации, так как они имеют симметричную прямоугольную форму волны с равной продолжительностью полупериодов. Практически все цифровые логические схемы используют сигналы в виде меандра на своих входах и выходах.

Так как форма меандра симметрична, и каждая половина цикла одинакова, то длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой). Для меандров, используемых в качестве тактирующих сигналов в цифровых схемах, длительность положительного импульса называется временем заполнения периода.

Для меандра, время заполнения

*** QuickLaTeX cannot compile formula: \tau *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37

равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T), то частота меандра:

*** QuickLaTeX cannot compile formula: \ *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37

Например, для сигнала с временем заполнения равным 10 мс, его частота равна:

*** QuickLaTeX cannot compile formula: f = \frac{1}{(10+10) \cdot 10^{-3}c} = 50 *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37

Гц

Меандры используются в цифровых системах для представления уровня логической «1» большими значениями его амплитуды и уровня логического «0» маленькими значениями амплитуды.

Если время заполнения, не равно 50% от длительности его периода, то такой сигнал уже представялет более общий случай и называется прямоугольным сигналом. В случае, или если время положительной части периода сигнала мало, то такой сигнал, является импульсом.

Гармонические колебания

На хабре было несколько статей по преобразованию Фурье и о всяких красивостях типа Цифровой Обработки Сигналов (ЦОС), но неискушённому пользователю совершенно не понятно, зачем всё это нужно и где, а главное как это применить.

АЧХ шума.

Лично мне после прочтения этих статей (например, этой ) не стало понятно, что это и зачем оно нужно в реальной жизни, хотя было интересно и красиво. Хочется не просто поглядеть красивые картинки, а так сказать, ощутить нутром, что и как работает. И я приведу конкретный пример с генерацией и обработкой звуковых файлов. Можно будет и послушать звук, и поглядеть его спектр, и понять, почему это так. Статья не будет интересна тем, кто владеет теорией функций комплексной переменной, ЦОС и прочими страшными темами. Она скорее для любопытствующих, школьников, студентов и им сочувствующих :).

Сразу оговорюсь, я не математик, и многие вещи могу даже сказать неправильно (поправляйте личным сообщением), и данную статью пишу, опираясь на собственный опыт и собственное понимание текущих процессов. Если вы готовы, то поехали.

Пару слов о матчасти

Если мы вспомним школьный курс математики, то для построения графика синуса мы использовали круг. В общем-то так и получается, что вращательное движение можно превратить в синусоиду (как и любое гармоническое колебание). Самое лучшая иллюстрация этого процесса приведена в википедии

Гармонические колебания

Т.е. фактически график синуса получается из вращения вектора, который описывается формулой:

f(x) = A sin (ωt + φ),

где A — длина вектора (амплитуда колебаний), φ — начальный угол (фаза) вектора в нулевой момент времени, ω — угловая скорость вращения, которая равна:

ω=2 πf, где f — частота в Герцах.

Как мы видим, что зная частоту сигнала, амплитуду и угол, мы можем построить гармонический сигнал.

Магия начинается тогда, когда оказывается, что представление абсолютно любого сигнала можно представить в виде суммы (зачастую бесконечной) различных синусоид. Иначе говоря, в виде ряда Фурье. Я приведу пример из английской википедии. Для примера возьмём пилообразный сигнал.

Пилообразный сигнал

Его сумма будет представлена следующей формулой:

Если мы будем по очерёдно суммировать, брать сначала n=1, затем n=2 и т.д., то увидим, как у нас гармонический синусоидальный сигнал постепенно превращается в пилу:

Наверное красивее всего это иллюстрирует одна программа, найденная мной на просторах сети. Выше уже говорилось, что график синуса является проекцией вращающегося вектора, а как же быть в случае более сложных сигналов? Это, как ни странно, проекция множества вращающихся векторов, а точнее их суммы, и выглядит это всё так:

Вектора рисуют пилу.

Вообще рекомендую сходить самим по ссылке и попробовать самим поиграться с параметрами, и посмотреть как меняется сигнал. ИМХО более наглядной игрушки для понимания я ещё не встречал.

Ещё следует заметить, что есть обратная процедура, позволяющая получить из данного сигнала частоту, амплитуду и начальную фазу (угол), которое называется Преобразование Фурье.

Разложение в ряд Фурье некоторых известных периодических функций (отсюда)

Я детально на нём останавливаться не буду, но покажу, как это можно применить по жизни. В списке литературы порекомендую то, где можно почитать подробнее о матчасти.

Переходим к практическим упражнениям!

Мне кажется, что каждый студент задаётся вопросом, сидя на лекции, например по матану: зачем мне весь этот бред? И как правило, не найдя ответа в обозримом будущем, к сожалению, теряет интерес к предмету. Поэтому я сразу покажу практическое применение данных знаний, а вы эти знания уже будете осваивать сами :).

Всё дальнейшее я буду реализовывать на сях. Делал всё, конечно, под Linux, но никакой специфики не использовал, по идее программа будет компилироваться и работать под другими платформами.

Для начала напишем программу для формирования звукового файла. Был взят wav-файл, как самый простой. Прочитать про его структуру можно тут. Если кратко, то структура wav-файла описывается так: заголовок, который описывает формат файла, и далее идёт (в нашем случае) массив 16-ти битных данных (остроконечник) длиной: частота_дискретизации*t секунд или 44100*t штук.

Для формирования звукового файла был взят пример здесь. Я его немного модифицировал, исправил ошибки, и окончательная версия с моими правками теперь лежит на гитхабе тут

github.com/dlinyj/generate_wav

Сгенерируем двухсекундный звуковой файл с чистым синусом частотой 100 Гц. Для этого модифицируем программу таким образом:

#define S_RATE (44100) //частота дискретизации #define BUF_SIZE (S_RATE*10) /* 2 second buffer */ …. int main(int argc, char * argv[]) { … float amplitude = 32000; //берём максимальную возможную амплитуду float freq_Hz = 100; //частота сигнала /* fill buffer with a sine wave */ for (i=0; i

Обращаю внимание, что формула чистого синуса соответствует той, о которой мы говорили выше. Амплитуда 32000 (можно было взять 32767) соответствует значению, которое может принимать 16-ти битное число (от минус 32767 до плюс 32767).

В результате получаем следующий файл (можно его даже послушать любой звуковоспроизводящей программой). Откроем данный файл audacity и увидим, что график сигнала в действительности соответствует чистому синусу:

Чистый ламповый синус

Поглядим спектр этого синуса (Анализ->Построить график спектра)

График спектра

Виден чистый пик на 100 Гц (логарифмический масштаб). Что такое спектр? Это амплитудно-частотная характеристика. Существует ещё фазочастотная характеристика. Если помните, выше я говорил, что для построения сигнала надо знать его частоту, амплитуду и фазу? Так вот, можно из сигнала получить эти параметры. В данном случае у нас график соответствий частот амплитуде, при чём амплитуда у нас не в реальных единицах, а в Децибелах.

Величина, выраженная в децибелах, численно равна десятичному логарифму безразмерного отношения физической величины к одноимённой физической величине, принимаемой за исходную, умноженному на десять.

В данном случае просто логарифм амплитуды, умноженный на 10. Логарифмический масштаб удобно использовать при работе с сигналами.

Мне, честно говоря, не очень нравится анализатор спектра в этой программе, поэтому я решил написать свой с блекджеком и шлюхами, тем более, что это несложно.

Пишем свой анализатор спектра

Здесь может быть скучно, поэтому можете перейти сразу к следующей главе.

Поскольку я прекрасно понимаю, что тут портянки кода размещать нет смысла, те, кому реально интересно — сами найдут и поковыряют, а тем, кому это неинтересно, будут скучать, то я остановлюсь только на основных моментах написания анализатора спектра wav-файла.

Во-первых, нам wav-файл необходимо читать. Там необходимо прочитать заголовок, чтобы понять, что содержит данный файл. Я не стал реализовывать море вариантов чтения данного файла, а остановился только на одном. Пример чтения файла был взят отсюда практически без изменений, ИМХО — отличный пример. Там же есть реализация на питоне.

Следующее, что нам нужно, это быстрое преобразование Фурье. Это то самое преобразование, которое позволяет получить из конечного набора точек вектора

исходных сигналов. Пусть вас пока это не пугает, дальше я объясню. Опять же, велосипед изобретать не стал, а взял готовый пример отсюда.

Я понимаю, что чтобы объяснить, как работает программа, надо объяснить, что такое быстрое преобразование Фурье, а это как минимум ещё на одну некислую статью.

Для начала алокируем массивы:

c = calloc(size_array*2, sizeof(float)); // массив поворотных множителей in = calloc(size_array*2, sizeof(float)); //входный массив out = calloc(size_array*2, sizeof(float)); //выходной массив

Скажу лишь, что в программе мы читаем данные в массив длиной size_array (которое берём из заголовка wav-файла).

while( fread(&value,sizeof(value),1,wav) ) { in[j]=(float)value; j+=2; if (j > 2*size_array) break; }

Массив для быстрого преобразования Фурье должен представлять собой последовательность {re[0], im[0], re[1], im[1],… re[fft_size-1], im[fft_size-1]}, где fft_size=1<< p — число точек БПФ. Объясняю нормальным языком: это массив комплексных чисел. Я даже боюсь представить, где используется комплексное преобразование Фурье, но в нашем случае мнимая часть у нас равна нулю, а действительная равна значению каждой точке масива. Ещё одна особенность именно быстрого преобразования Фурье, что оно обсчитывает массивы, кратные только степени двойки. В результате мы должны вычислить минимальную степень двойки:

int p2=(int)(log2(header.bytes_in_data/header.bytes_by_capture));

Логарифм от количество байт в данных, делённых на количество байт в одной точке.

После этого считаем поворотные множители:

fft_make(p2,c);// функция расчёта поворотных множителей для БПФ (первый параметр степень двойки, второй алокированный массив поворотных множителей).

И скармливаем наш считанный массив в преобразователь Фурье:

fft_calc(p2, c, in, out, 1); //(единица означает, что мы получаем нормализованный массив).

На выходе мы получаем комплексные числа вида {re[0], im[0], re[1], im[1],… re[fft_size-1], im[fft_size-1]}. Для тех, кто не знает, что такое комплексное число, поясню. Я не зря начал эту статью с кучи вращающихся векторов и кучи гифок. Так вот, вектор на комплесной плоскости определяется действительной координатой a1 и мнимой координатой a2. Или длиной (это у нас амплитуда Am) и углом Пси (фаза).

Вектор на комплексной плоскости

Обратите внимание, что size_array=2^p2. Первая точка массива соответствует частоте 0 Гц (постоянная), последняя точка соответствует частоте дискретизации, а именно 44100 Гц. В результате мы должны рассчитать частоту, соответствующей каждой точке, которые будут отличаться на частоту дельта:

double delta=((float)header.frequency)/(float)size_array; //частота дискретизации на размер массива.

Алокируем массив амплитуд:

double * ampl; ampl = calloc(size_array*2, sizeof(double));

И смотрим на картинку: амплитуда — это длина вектора. А у нас есть его проекции на действительную и мнимую ось. В результате у нас будет прямоугольный треугольник, и тут мы вспоминаем теорему Пифагора, и считаем длину каждого вектора, и сразу пишем её в текстовый файл:

for(i=0;i<(size_array);i+=2) { fprintf(logfile,»%.6f %f\n»,cur_freq, (sqrt(out
*out+out[i+1]*out[i+1]))); cur_freq+=delta; } В результате получаем файл примерно такого вида: … 11.439514 10.943008 11.607742 56.649738 11.775970 15.652428 11.944199 21.872342 12.112427 30.635371 12.280655 30.329171 12.448883 11.932371 12.617111 20.777617 …
Окончательная версия программы обитает на гитхабе вот тут: github.com/dlinyj/fft

Пробуем!

Теперь скармливаем получившейся программе тот звуковой файл синуса

./fft_an ../generate_wav/sin\ 100\ Hz.wav format: 16 bits, PCM uncompressed, channel 1, freq 44100, 88200 bytes per sec, 2 bytes by capture, 2 bits per sample, 882000 bytes in data chunk=441000 log2=18 size array=262144 wav format Max Freq = 99.928 , amp =7216.136

И получаем текстовый файл АЧХ. Строим его график с помощью гнуплота

Скрипт для построения:

#! /usr/bin/gnuplot -persist set terminal postscript eps enhanced color solid set output «result.ps» #set terminal png size 800, 600 #set output «result.png» set grid xtics ytics set log xy set xlabel «Freq, Hz» set ylabel «Amp, dB» set xrange [1:22050] #set yrange [0.00001:100000] plot «test.txt» using 1:2 title «AFC» with lines linestyle 1

Обратите внимание на ограничение в скрипте на количество точек по X: set xrange [1:22050]. Частота дискретизации у нас 44100, а если вспомнить теорему Котельникова, то частота сигнала не может быть выше половины частоты дискретизации, следовательно сигнал выше 22050 Гц нас не интересует. Почему так, советую прочитать в специальной литературе. Итак (барабанная дробь), запускаем скрипт и лицезреем:

Спектр нашего сигнала

Обратите внимание на резкий пик на частоте 100 Гц. Не забывайте, что по осям — логарифмический масштаб! Шерсть справа, как я думаю, ошибки преобразования Фурье (тут на память приходят окна).

А давайте побалуем?

А давайте! Давайте поглядим спектры других сигналов!

Вокруг шум…

Для начала построим спектр шума. Тема про шумы, случайные сигналы и т.п. достойна отдельного курса. Но мы её коснёмся слегка. Модифицируем нашу программу генерации wav-файла, добавим одну процедуру: double d_random(double min, double max) { return min + (max — min) / RAND_MAX * rand(); }
она будет генерировать случайное число в заданном диапазоне. В результате main будет выглядеть так:

int main(int argc, char * argv[]) { int i; float amplitude = 32000; srand((unsigned int)time(0)); //инициализируем генератор случайных чисел for (i=0; i

Сгенерируем файл, (рекомендую к прослушиванию). Поглядим его в audacity.

Сигнал в audacity

Поглядим спектр в программе audacity.

Спектр

И поглядим спектр с помощью нашей программы:

Наш спектр

Хочу обратить внимание на очень интересный факт и особенность шума — он содержит в себе спектры всех гармоник. Как видно из графика, спектр вполне себе ровный. Как правило, белый шум используется для частотного анализа пропускной способности, например, аудиоаппаратуры. Существуют и другие виды шумов: розовый, синий и другие

. Домашнее задание — узнать, чем они отличаются.

А компот?

А теперь давайте посмотрим другой интереснейший сигнал — меандр. Я там выше приводил табличку разложений различных сигналов в ряды Фурье, вы поглядите как раскладывается меандр, выпишите на бумажку, и мы продолжим.

Для генерации меандра с частотой 25 Гц мы модифицируем в очередной раз наш генератор wav-файла:

int main(int argc, char * argv[]) { int i; short int meandr_value=32767; /* fill buffer with a sine wave */ for (i=0; i

В результате получим звуковой файл (опять же, советую послушать), который сразу надо посмотреть в audacity

Его величество — меандр или меандр здорового человека

Не будем томиться и поглядим его спектр:

Спектр меандра

Пока не очень что-то понятно, что такое… А давайте поглядим несколько первых гармоник:

Первые гармоники

Совсем другое дело! Ну-ка поглядим табличку. Смотрите-ка, у нас есть только 1, 3, 5 и т.д., т.е. нечётные гармоники. Мы так и видим, что у нас первая гармоника 25 Гц, следующая (третья) 75 Гц, затем 125 Гц и т.д., при этом у нас амплитуда постепенно уменьшается. Теория сошлась с практикой! А теперь внимание! В реальной жизни сигнал меандра у нас имеет бесконечную сумму гармоник всё более и более высокой частоты, но как правило, реальные электрические цепи не могут пропускать частоты выше какой-то частоты (в силу индуктивности и ёмкости дорожек). В результате на экране осциллографа можно часто увидеть вот такой сигнал:

Меандр курильщика

Эта картинка прям как картинка из википедии, где для примера меандра берутся не все частоты, а только первые несколько.

Сумма первых гармоник, и как меняется сигнал

Меандр так же активно используется в радиотехнике (надо сказать, что — это основа всей цифровой техники), и стоит понимать что при длинных цепях его может отфильтровать так, что, родная мама не узнает. Его так же используют для проверки АЧХ различных приборов. Ещё интересный факт, что глушилки телевизоров работали именно по принципу высших гармоник, когда сама микросхема генерировала меандр десятки МГц, а его высшие гармоники могли иметь частоты сотни МГц, как раз на частоте работы телевизора, и высшие гармоники успешно глушили сигнал вещания телевизора.

Вообще тема подобных экспериментов бесконечная, и вы можете теперь сами её продолжить.

Заключение

В заключении хочу сказать, что математика — царица наук, но без реального применения многие люди теряют к ней интерес. Надеюсь, данный пост подстегнёт вас к изучению такого замечательного предмета, как обработка сигналов, и вообще аналоговой схемотехнике (затыкайте уши, чтобы не вытекали мозги!). Удачи!

Прямоугольный сигнал

Прямоугольные сигналы отличаются от меандров тем, что длительности положительной и отрицательной частей периода не равны между собой. Прямоугольные сигналы поэтому классифицируются как несимметричные сигналы.

В данном случае я изобразил сигнал, принимающий только положительные значения, хотя, в общем случае, отрицательные значения сигнала могут быть значительно ниже нулевой отметки.

На изображенном примере, длительность положительного импульса больше, чем длительность отрицательного, хотя, это и не обязательно. Главное, чтобы форма сигнала была прямоугольной.

Отношение периода повторения сигнала

*** QuickLaTeX cannot compile formula: T *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37 , к длительности положительного импульса *** QuickLaTeX cannot compile formula: \tau *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37

, называют скважностью:

Величину обратную скважности называют коэффициентом заполнения (duty cycle):

Пример расчета
Пусть имеется прямоугольный сигнал с импульсом длительностью 10мс и коэффициентом заполнения 25%. Необходимо найти частоту этого сигнала.
Коэффициент заполнения равен 25% или ¼, и совпадает с шириной импульса, которая составляет 10мс. Таким образом, период сигнала должен быть равен: 10мс (25%) + 30мс (75%) = 40мс (100%).
*** QuickLaTeX cannot compile formula: f = \frac{1}{T} = \frac{1}{(10 + 30) \cdot 10^{-3}c} = 25 *** Error message: Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.) These links might help in finding solution: https://wordpress.org/extend/plugins/core-control/ https://wordpress.org/support/topic/an-unexpected-http-error-occurred-during-the-api-request-on-wordpress-3?replies=37
Гц

Прямоугольные сигналы могут использоваться для регулирования количества энергии, отдаваемой в нагрузку, такую, например, как лампа или двигатель, изменением скважности сигнала. Чем выше коэффициент заполнения, тем больше среднее количество энергии должно быть отдано в нагрузку, и, соответственно, меньший коэффициент заполнения, означает меньшее среднее количество энергии, отдаваемое в нагрузку. Отличным примером этого является использование широтно-импульсной модуляции в регуляторах скорости. Термин широтно-импульсная модуляция (ШИМ) буквально и означает «изменение ширины импульса».

ШИМ сигнал

Аппаратный

Для генерации ШИМ сигнала с заданным заполнением есть стандартная функция analogWrite(pin, duty), подробнее обсуждали в уроке про ШИМ сигнал, а частоту можно изменить перенастройкой таймера, как в уроке об увеличении частоты ШИМ. На самом деле таймеры позволяют настроить ШИМ сигнал с более точной или более высокой частотой и другими диапазонами заполнения (до 10 бит), но в ядре Arduino это не предусмотрено. Если такое будет нужно, можно воспользоваться библиотекой GyverPWM. Пример:

pinMode(10, OUTPUT); // запустить ШИМ на D10 с частотой 150’000 Гц, режим FAST_PWM PWM_frequency(10, 150000, FAST_PWM);

Программный ШИМ

Программная генерация ШИМ сигнала может пригодиться, если не хватает лишнего таймера или частота ШИМ низкая и не повлияет на остальной код, а он на неё. ШИМ сигнал на “миллисе” можно организовать вот таким образом, переключая выход по двум периодам:

Софт ШИМ на millis()

Функцию PWMgen(заполнение) в данной реализации нужно вызывать как можно чаще в основном цикле программы:

#define PWM_PRD 20 // период ШИМ, мс #define PWM_PIN 13 // пин ШИМ void setup() { pinMode(PWM_PIN, OUTPUT); } void loop() { PWMgen(analogRead(0) / 4); // берём значение ШИМ с А0, 0.. 255 } void PWMgen(byte duty) { static uint32_t tmr; static bool flag; if (duty == 0) digitalWrite(PWM_PIN, LOW); else if (duty == 255) digitalWrite(PWM_PIN, HIGH); else { int prd = (PWM_PRD * duty) >> 8; // равносильно / 255 if (millis() — tmr >= (flag ? prd : PWM_PRD — prd)) { tmr = millis(); digitalWrite(PWM_PIN, flag = !flag); } } }

Здесь мы на каждом вызове считаем новый период переключения, тратя на это какое-то время. Можно считать период в отдельной функции, а сам ШИМ генерировать отдельно. Реализацию можно посмотреть в библиотеке PWMrelay.

Полуаппаратный ШИМ

Можно снизить нагрузку на процессор, отдав счёт времени аппаратному таймеру. Примеры на базе GyverTimers (для ATmega328, 2560):

8 бит ШИМ

// частота ШИМ = ~ (частота вызова tick / 256); #define PWM_FREQ 100 // частота ШИМ #define PWM_PIN 13 // пин ШИМ #include // подключаем библиотеку аппаратных таймеров volatile uint8_t pwm_duty = 0; // переменная для хранения заполнения шим 0-255 volatile uint8_t counter = 0; // аналог счетного регистра таймера void setup() { Timer2.setFrequency(256L * PWM_FREQ); // частота прерываний Timer2.enableISR(); // включаем прерывания таймера pinMode(PWM_PIN, OUTPUT); // пин как выход } void loop() { // задаём скважность ШИМ потенциометром с пина А0 pwm_duty = analogRead(0) / 4; // 1023 -> 255 // задержка задания значения, чтобы избежать скачков delay(100); } // прерывание таймера ISR(TIMER2_A) { if (!pwm_duty) digitalWrite(PWM_PIN, LOW); // заполнение ШИМ == 0 else { if (!counter) digitalWrite(PWM_PIN, HIGH); // при обнулении счётчика HIGH else if (counter == pwm_duty) digitalWrite(PWM_PIN, LOW); // при совпадении LOW counter++; } }

Настройка разрядности

// частота ШИМ = ~ (частота вызова tick / (глубина ШИМ + 1)); #define PWM_DEPTH 100 // разрядность ШИМ #define PWM_PIN 13 // пин ШИМ #include // подключаем библиотеку аппаратных таймеров volatile uint8_t pwm_duty = 0; // переменная для хранения заполнения шим 0-255 volatile uint8_t counter = 0; // аналог счетного регистра таймера void setup() { Timer2.setPeriod(10); // прерывания по таймеру с частотой 100 кгц Timer2.enableISR(); // включаем прерывания таймера 2 pinMode(PWM_PIN, OUTPUT); // устанавливаем пин на выход } void loop() { // получить заполнение ШИМ с потенциометра A0 pwm_duty = map(analogRead(A0), 0, 1023, 0, PWM_DEPTH); // задержка задания значения, чтобы избежать скачков delay(100); } ISR(TIMER2_A) { if (!pwm_duty) digitalWrite(PWM_PIN, LOW); // заполнение ШИМ == 0 else { if (!counter) digitalWrite(PWM_PIN, HIGH); // при обнулении счётчика HIGH else if (counter == pwm_duty) digitalWrite(PWM_PIN, LOW); // при совпадении LOW if (++counter > PWM_DEPTH) counter = 0; // проверка на переполнение } }

Как известно, digitalWrite() является очень тяжёлой и долгой функцией, и для генерации софт ШИМ рекомендуется заменить её чем-то более быстрым, например прямым обращением к регистру или вот такой конструкцией (для ATmega328p):

void digitalWriteFast(uint8_t pin, bool x) { if (pin < { bitWrite(PORTD, pin, x); } else if (pin < 14) { bitWrite(PORTB, (pin — 8), x); } else if (pin < 20) { bitWrite(PORTC, (pin — 14), x); } }

Если не хватает количества стандартных ШИМ-выходов, можно поднять полуаппаратный ШИМ на таймере на несколько пинов сразу:

Многоканальный софт ШИМ

#define PWM_FREQ 100 // частота ШИМ const uint8_t pwm_pins[] = {2, 3, 4, 5}; // пины #include // подключаем библиотеку аппаратных таймеров const uint8_t PWM_PINS = sizeof(pwm_pins); volatile uint8_t pwm_duty[PWM_PINS]; // переменная для хранения заполнения шим 0-255 volatile uint8_t counter; // счётчик void setup() { Timer2.setFrequency(256L * PWM_FREQ); // прерывания по таймеру Timer2.enableISR(); // включаем прерывания таймера 2 // устанавливаем пины на выход for (int i = 0; i < PWM_PINS; i++) pinMode(pwm_pins, OUTPUT); // заполнение pwm_duty[0] = 10; pwm_duty[1] = 20; pwm_duty[2] = 128; pwm_duty[3] = 128; } void loop() { } // прерывание таймера ISR(TIMER2_A) { for (int i = 0; i < PWM_PINS; i++) { if (!pwm_duty) digitalWrite(pwm_pins, LOW); // заполнение ШИМ == 0 else { if (!counter) digitalWrite(pwm_pins, HIGH); // при обнулении счётчика HIGH else if (counter == pwm_duty) digitalWrite(pwm_pins, LOW); // при совпадении LOW } } counter++; }

Этот алгоритм является не самым оптимальным, более интересный можно посмотреть в GyverHacks.

Примечание: во всех трёх алгоритмах используется проверка совпадения со счётчиком counter == pwm_duty. Это сильно снижает использование процессорного времени в прерывании, но при резком уменьшении заполнения может приводить к одиночным “вспышкам” заполнения до максимума, так как условие не выполнится. Для более плавной работы можно сделать counter >= pwm_duty, тогда условие будет каждый раз “подстраиваться” под новое значение заполнения, но установка пина будет осуществляться на каждом тике!

Можно ввести буферизацию заполнения ШИМ и брать новое значение только при нулевом значении счётчика, это решит проблему:

ШИМ с буферизацией

// софт шим с буферизацией #define PWM_FREQ 100 // частота ШИМ #define PWM_PIN 13 // пин ШИМ #include // подключаем библиотеку аппаратных таймеров volatile uint8_t pwm_duty = 0; // переменная для хранения заполнения шим 0-255 volatile uint8_t counter = 0; // аналог счетного регистра таймера volatile uint8_t real_duty = 0; void setup() { Timer2.setFrequency(256L * PWM_FREQ); // частота прерываний Timer2.enableISR(); // включаем прерывания таймера pinMode(PWM_PIN, OUTPUT); // пин как выход } void loop() { // задаём скважность ШИМ потенциометром с пина А0 pwm_duty = analogRead(0) / 4; // 1023 -> 255 } // прерывание таймера ISR(TIMER2_A) { if (!pwm_duty) digitalWrite(PWM_PIN, LOW); // заполнение ШИМ == 0 else { if (!counter) { // при счётчике == 0 digitalWrite(PWM_PIN, HIGH); // HIGH real_duty = pwm_duty; // берём из «буфера» } else if (counter == real_duty) digitalWrite(PWM_PIN, LOW); // при совпадении LOW counter++; } }

Можно применить буферизацию и к остальным алгоритмам.

Библиотека Servo

Как известно, RC сервоприводы управляются при помощи ШИМ сигнала с частотой ~50 Гц и длительностью импульса от~500 до ~2500 микросекунд. В стандартной библиотеке Servo.h реализована генерация полуаппаратного ШИМ сигнала, причём количество пинов можно менять во время работы. Библиотеку можно использовать как генерацию ШИМ, если его параметры подходят для использования.

Треугольные сигналы

Треугольные сигналы, как правило, это двунаправленные несинусоидальные сигналы, которые колеблются между положительным и отрицательным пиковыми значениями. Треугольный сигнал представляет собой относительно медленно линейно растущее и падающее напряжение с постоянной частотой. Скорость, с которой напряжение изменяет свое направление равна для обоих половинок периода, как показано ниже.

Как правило, для треугольных сигналов, продолжительность роста сигнала, равна продолжительности его спада, давая тем самым 50% коэффициент заполнения. Задав амплитуду и частоту сигнала, мы можем определить среднее значение его амплитуды.

В случае несимметричной треугольной формы сигнала, которую мы можем получить изменением скорости роста и спада на различные величины, мы имеем еще один тип сигнала известный под названием пилообразный сигнал.

Беседа седьмая. Сигналы прямоугольной формы. Ограничение. Дифференцирование и интегрирование

Незнайкин чрезвычайно обеспокоен: он привык к технике низких частот, где необходимо сохранять форму сигнала, и теперь, наблюдая, как Любознайкин систематически деформирует сигнал, он пришел в полное замешательство. Незнайкин начинает усваивать, что такое ограничение сигнала сверху, как превращают медленное изменение напряжения в скачкообразное, затем он постигает тайны дифференцирующих и интегрирующих схем. Наступает неизбежное (вопреки его желанию и общеизвестному ужасу перед математикой) — его заставляют проглотить определение (упрощенное!) производных и интегралов… и он понимает, что эпю значительно проще, чем обычно думают.

Сигналы прямоугольной формы. Ограничение. Дифференцирование и интегрирование

Незнайкин — Дорогой Любознайкин, прошлый раз я забыл задать тебе один вопрос.

Скажи, пожалуйста, насколько верно воспроизводят сигналы различные «суперусилители», о которых ты мне рассказывал?

Любознайкин — Точность воспроизведения прекрасная у всех систем, собранных по схеме катодного или эмиттерного повторителя и, особенно, у «суперэмиттерного повторителя» на двух взаимно дополняющих транзисторах, так как эта схема характеризуется глубокой отрицательной обратной связью.

Само собой разумеется, что ты можешь осуществить эту верность воспроизведения лишь в том случае, если не перегрузишь схему, т. е. не заставишь ее давать на выходе наибольший ток или наибольшее напряжение, но в промышленной электронике во многих случаях линейность не является основным требованием, предъявляемым к усилителю, иногда даже наоборот…

Умышленно вносимые искажения

Н. — Вот как! Так значит сигнал деформируют, полагаясь на волю случая или в силу извращенности?

Л. — Да, сигнал деформируют, но не по воле случая. Что же касается извращенности, то ты можешь и, вероятно, предложишь мне основать АЗСОПД (Ассоциацию Защитников Сигналов От Порочного Деформирования).

Н. — Надеюсь, что ты вступишь в эту ассоциацию. Но как могут деформированные сигналы создавать неискаженный звук?

Л. — На этот раз выбрось из головы свои идеи о звукофикации и музыкальности. Воспроизведение звука — одна из сфер приложения радиоэлектроники, по она ни коим образом не исчерпывает всей радиоэлектроники, точно так же, как и электричество служит не только для питания электроплиток. Напряжение с выхода твоего усилителя может приводить в действие не только громкоговоритель. И, если ты хочешь, чтобы оно, например, включало реле, разве напряжение обязательно должно быть синусоидальным?

Н. — Согласен. А каким деформациям ты подвергнешь сигнал?

Л. — Мы начнем с ограничения сигнала сверху, так как этот практичный метод позволяет уравнять величину сигналов с различной амплитудой. Такую задачу можно успешно решить путем использования простого диода. Как ты видишь, изображенная на рис. 53 схема пропустит на выход только положительную часть входного сигнала UBX.

Н. — Это понять легко. Но для чего понадобился здесь резистор R

Л. — Его роль не так очевидна. Представь себе, что на выход подключают какую-нибудь нагрузку, использующую напряже

ограничитель Рис. 53. Ограничитель. На выход проходит только положительная часть поступающего на вход напряжения.

ограничитель Рис. 54. Ограничитель с параллельно включенным диодом, замыкающим накоротко цепь для отрицательной части входного напряжения UBblx .

Пилообразный сигнал

Пилообразный сигнал — это еще один тип периодического сигнала. Как следует из названия, форма такого сигнала напоминает зубья пилы. Пилообразный сигнал может иметь зеркальное отражение самого себя, имея либо медленный рост, но очень крутой спад, или чрезвычайно крутой, почти вертикальный рост и медленный спад.

Пилообразный сигнал с медленным ростом является более распространенным из двух типов сигналов, являющийся, практически, идеально линейным. Пилообразный сигнал генерируется большинством функциональных генераторов и состоит из основной частоты (f) и четных гармоник. Это означает, с практической точки зрения, что он богат гармониками, и в случае, например, с музыкальными синтезаторами, для музыкантов дает качественный звук без искажений.