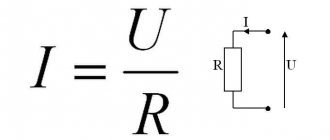Закон Ома для замкнутой цепи показывает — значение тока в реальной цепи зависит не только от сопротивления нагрузки, но и от сопротивления источника.
Формулировка закона Ома для замкнутой цепи звучит следующим образом: величина тока в замкнутой цепи, состоящей из источника тока, обладающего внутренним и внешним нагрузочным сопротивлениями, равна отношению электродвижущей силы источника к сумме внутреннего и внешнего сопротивлений.
Впервые зависимость тока от сопротивлений была экспериментально установлена и описана Георгом Омом в 1826 году.
Формула закона Ома для замкнутой цепи записывается в следующем виде:
где:
- I [А] – сила тока в цепи,
- ε [В] – ЭДС источника напряжения,
- R [Ом] – сопротивление всех внешних элементов цепи,
- r [Ом] – внутреннее сопротивление источника напряжения
Первоначальная и современная формулировка
Этот, на первый взгляд, простой закон был сформулирован немецким физиком Георгом Омом в 1826 году. Соответствующую научную статью он опубликовал в следующем году.
Интересно отметить, что появление этой работы не вызвало ажиотажа. Научная общественность оценила открытие Ома лишь после публикации работ физика Пулье аналогичного содержания в 1830 году. В 1833 Ом получил степень доктора в Нюрнбергском университете. В 1872 году единица измерения сопротивления стала называться Омом. В самой простой форме закон для участка цепи звучит так:
Закон носит эмпирический характер, так как он выражает обобщенный анализ большого количества опытных данных.
Сейчас формула закона Ома для полной электрической цепи имеет следующий вид:
I = ℰ / (R+r).
Здесь:
- ℰ — ЭДС источника напряжения, В;
- I — сила тока в цепи, А.
- R — общее сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Закон Ома для полной цепи учитывает полное сопротивление, которое представляет собой сумму сопротивления цепи R и внутреннего сопротивления источника тока r.
Георг Ом первоначально сформулировал его по-другому. Закон Ома для замкнутой цепи выглядел так:
X = a / ( b + l ), где
- a — величина, характеризующая источник тока. Сейчас говорят, что это электродвижущая сила источника тока;
- b представляет собой свойство электрической установки, которое теперь рассматривается в качестве внутреннего сопротивления источника тока;
- l — величина, зависящая от длины используемых проводов (в современных терминах она соответствует сопротивлению электрической цепи).
Как видно, закон Ома, применяемый для полной электрической цепи, в обоих вариантах имеет одинаковую формулировку.
Также применяется закон Ома в дифференциальной форме. В данном случае рассматриваются очень малые величины. Но это позволяет применять интегральное и дифференциальное исчисление для сложных случаев.
Закон Джоуля-Ленца
Закон Джоуля — Ленца гласит: количество теплоты, выделяемое в проводнике на участке электрической цепи с сопротивлением $R$ при протекании по нему постоянного тока $I$ в течение времени $t$ равно произведению квадрата тока на сопротивление и время:
$Q=I^2Rt$
Закон был установлен в 1841 г. английским физиком Дж. П. Джоулем, а в 1842 г. подтвержден точными опытами русского ученого Э. X. Ленца. Само же явление нагрева проводника при прохождении по нему тока было открыто еще в 1800 г. французским ученым А. Фуркруа, которому удалось раскалить железную спираль, пропустив через нее электрический ток.
Из закона Джоуля — Ленца следует, что при последовательном соединении проводников, поскольку ток в цепи всюду одинаков, максимальное количество тепла будет выделяться на проводнике с наибольшим сопротивлением. Это используется в технике, например, для распыления металлов.
При параллельном соединении все проводники находятся под одинаковым напряжением, но токи в них разные. Из формулы ($Q=I^2Rt$) следует, что, так как, согласно закону Ома $I={U}/{R}$, то
$Q={U^2t}/{R}$
Следовательно, на проводнике с меньшим сопротивлением будет выделяться больше тепла.
Если в формуле ($A=IUt$) выразить $U$ через $IR$, воспользовавшись законом Ома, получим закон Джоуля-Ленца. Это лишний раз подверждает тот факт, что работа тока расходуется на выделение тепла на активном сопротивлении в цепи.
Практическое применение
В большинстве случаев внутреннее сопротивление источника тока считают относительно малым по сравнению с тем, которое есть в электрической цепи. В этом случае применяется закон Ома для замкнутой цепи в сокращенной формулировке: I = U / R.
Чтобы лучше понять, какие физические процессы происходят в электрической цепи, нужно учитывать следующее:
- В источнике тока наблюдаются процессы, которые приводят к тому, что на клеммах образуется разность потенциалов. При подключении к ним электрической цепи по ней идёт ток. Принято считать, что он проходит от положительного потенциала к отрицательному.
- Ток представляет собой упорядоченное движение электронов. В веществе находится огромное количество этих частиц, которые перемещаются с большой скоростью от отрицательного потенциала к положительному.
- Скорость движения электронов зависит от материала проводника, через который они проходят, от его сечения и длины. Если последняя в 2 раза будет увеличена, то это удвоит сопротивление.
В электрической цепи используются резисторы в тех случаях, когда для работы прибора требуется строго определённое сопротивление. Если клеммы источника тока, говоря простыми словами, соединить напрямую, то сопротивление будет малым, а ток относительно большим. С одной стороны, большой ток в некоторых случаях способен расплавить провод, с другой он приводит к ускоренной разрядке батареи.
В веществе движение электронов не является свободным. Перемещаясь, частицы должны преодолевать сопротивление, расходуя на это свою энергию. Величина сопротивления зависит от конкретного материала. В проводниках электроны двигаются относительно легко. Через изоляторы ток пройти не может, за исключением тех случаев, когда подаётся настолько высокое напряжение, что такая ситуация создает пробой.
В полупроводниках происходят более сложные процессы, поскольку они отличаются жесткой кристаллической структурой. При наличии примесей определённого типа может возникать электронная или дырочная проводимость. Ток может представлять собой движение, как электронов, так и дырок.
Более точную характеристику сопротивления можно получить из следующей формулы:
С помощью удельного сопротивления можно охарактеризовать электрические свойства определённого вещества. Эта величина представляет собой сопротивление, которое имеет отрезок провода из данного материала длиной 1 м и площадью сечения 1 кв. мм.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.
Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.
Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.
Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.
Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов. Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Источники
- https://tel-spb.ru/ohm/
- https://elektroznatok.ru/info/teoriya/zakon-oma
- https://ElectroInfo.net/teorija/vse-o-zakone-oma-prostymi-slovami-s-primerami-dlja-chajnikov.html
- https://radioprog.ru/post/920
- https://YDoma.info/ehlektrotekhnika/electricity-zakon-oma.html
- https://toe.1c-umi.ru/lekcii/lekciya_6_-_zakon_oma/
[свернуть]
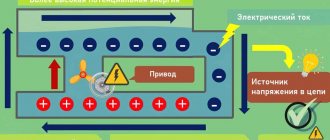
Сопротивление источника тока
Закон Ома для полной электрической цепи и формулы для расчета ее параметров характеризируют не только ток, проходящий через цепь, но и тот, который существует внутри источника тока. Закон Ома для участка цепи не учитывает наличие этой величины.
Батарея аккумулятора обеспечивает перемещение электронов от положительной клеммы к отрицательной. Через электрическую цепь они постоянно движутся в противоположном направлении. Уменьшение их количества на отрицательной клемме и избыток на положительной постоянно компенсируются процессами, происходящими внутри устройства.
Такое движение электронов также является электрическим током. При этом частицам приходится преодолевать внутреннее сопротивление источника тока. При увеличении температуры сопротивление может меняться, характер изменения зависит от конкретного материала.
Кулон и электрический заряд
Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.
Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.
Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.
Эмпирический характер закона Ома
При изучении природы электричества путем научных исследований происходит формулировка тех или иных законов. Они отличаются межу собой не только своим содержанием, но и тем, как были выведены. Некоторые законы представляют собой следствие из более общих утверждений, другие являются удачной попыткой объяснить многократно наблюдаемые факты.
Закон Ома для однородного участка фактически является попыткой создать правило, которое соответствует большому количеству наблюдений и экспериментов. Его формулировка на протяжении веков подтверждалась на практике, приобретая силу фундаментального закона физики. Закон Ома, представленный в интегральной форме, даёт возможность производить расчёты для различных электрических цепей.
Свойства электрического тока
Направлением электрического тока принято считать движение свободных положительных зарядов. Ток называется постоянным, если его направление и сила постоянны во времени.
Электрическое поле величиной E действует на заряд величиной q с силой F, которая равна:
$ F = q * E $ (1).
В результате в проводнике возникает электрический ток. Для создания электрического поля E, к концам проводника должно быть приложено напряжение U, которое равно разности потенциалов φ1 и φ2 на концах проводника:
$ U = φ2 – φ1 $ (2),
при этом φ2 > φ1.
Единица электрического тока — ампер (А) — названа в честь французского физика Ампера. Эта единица является одной семи основных единиц в Международной системе СИ. Единицей измерения напряжений является вольт (В), названная в честь итальянского исследователя Алессандро Вольта.
Использование для переменного тока
Как известно, в цепи переменного тока действует как активное, так и реактивное сопротивление. Первое из них совпадает с тем, как понимали эту величину во времена Георга Ома. Однако индуктивное и емкостное сопротивления также тормозят движение электронов. В этом случае применяется закон Ома для переменного тока.
Чтобы использовать данный закон в таких цепях, вместо омического сопротивления следует рассматривать полное, которое учитывает суммарное воздействие активной и реактивной составляющих сопротивления.
В представленной схеме полное сопротивление обозначается как Z. Омическое, индуктивное и емкостное — соответственно R, XL и XC. Закон Ома для цепи переменного тока учитывает все эти разновидности. Формула расчёта подразумевает, что сложение сопротивлений происходит по правилу векторов.
Для определения всех сопротивлений используют прямоугольный треугольник, один катет которого выражает активное сопротивление, а второй – реактивное. Последнее равно разнице индуктивного и емкостного сопротивлений. Определение полного осуществляется по теореме Пифагора, согласно которой длина гипотенузы равна корню квадратному от суммы квадратов катетов.
Энергетический баланс на участке цепи
Если на участке цепи действуют сторонние силы, то следует говорить о трех членах в энергетическом балансе:
1) Чтобы найти количество выделившегося тепла, надо вычислить работу суммарного поля над зарядами цепи. Как утверждает обобщенный закон Ома, работа суммарного поля над единичным зарядом равна I
12
R
значит, за время
t
суммарное поле совершит работу
\(~Q = I_{12} Rq = I_{12} R(I_{12} t) = I^2_{12} Rt\)
(закон Джоуля—Ленца). Эта величина всегда положительна.
2) Работу сторонних сил над зарядами нужно трактовать как поступление энергии от неэлектростатических источников энергии. Она равна
\(~A_{st} = \varepsilon_{12} q = \varepsilon_{12} I_{12} t\) .
Эта величина может быть как положительной, так и отрицательной.
3) Работа электростатических сил над зарядами равна
\(~A_{el} = (\varphi_1 — \varphi_2)q = U_{12} I_{12} t\) .
Чтобы понять энергетический смысл этого выражения, заметим, что, в соответствии с обобщенным законом Ома,
\(~I_{12}Rq = (\varphi_1 — \varphi_2 + \varepsilon_{12}) q\) .
или
\(~Q = A_{el} + A_{st}\) .
Значит, исходя из закона сохранения энергии, можно утверждать, что работа электростатических сил на участке цепи равна энергии, поступившей в данный участок из оставшейся части цепи (т.е. из внешней цепи)
. Если эта работа отрицательна, то во внешней цепи работа электростатических сил положительна, т.е.
UI
имеет смысл энергии, переданной во внешнюю цепь. Таким образом, электростатические силы регулируют обмен энергией между частями цепи.
Обсудим два примера.
Рис. 5
КПД источника тока
Для вычисления коэффициента полезного действия надо разобраться, какая величина в данном конкретном случае играет роль полной (затраченной), работы, а какая — полезной работы.
Рассмотрим ситуацию, когда источник тока является источником энергии для внешней цепи (содержащей, например, идеальный резистор, на котором только выделяется тепло). В этом случае (рис.5,а) сторонние силы источника совершают положительную работу \(~A_{st} = \varepsilon It\), имеющую смысл полной (затраченной) работы, часть энергии \(~Q = I^2 rt\) теряется в источнике в виде тепла, а часть \(~A_{polezn} = (\varepsilon I — I^2 r)t = UIt\) передается во внешнюю цепь. Электростатические силы в самом источнике совершают отрицательную работу, а во внешней цепи — положительную.
КПД электромотора
Рассмотрим теперь случай, когда участок цепи получает энергию из внешней цепи, и эта энергия не преобразуется целиком в тепло, а частично идет на совершение работы. Это возможно только тогда, когда на участке есть сторонние силы (на идеальном резисторе вся энергия переходит в тепло). Эти сторонние силы действуют против тока, совершая отрицательную работу (рис.5,б), а работа против сторонних сил — положительная.
Например, при работе электромотора в обмотках вращающегося якоря возникает ЭДС электромагнитной индукции ε
. В этом случае положительная работа электростатических сил \(~A_{el} = UIt\) имеет смысл полной (затраченной) работы, часть энергии \(~Q = I^2 Rt\) теряется в виде тепла, а часть \(~A_{polezn} = (UI — I^2R)t = \varepsilon It\) представляет из себя полезную работу — механическую работу электромотора.
Аналогичные соотношения можно записать и во многих других случаях (например, при зарядке аккумулятора).
Применение на практике
Когда нужно работать с электрической цепью, важно знать напряжение, силу тока, сопротивление во всей цепи или на отдельных участках. Если известны две из этих величин, то с помощью закона Георга Ома можно узнать третью без проведения непосредственных измерений.
Иногда требуется использовать закон Ома для неоднородного участка цепи. В этом случае его разбивают на отдельные зоны и сначала проводят вычисления для них.
Поскольку от электрических параметров зависят тепловые или химические воздействия, применяя закон Ома можно рассчитать возможный эффект. В частности, знание таких особенностей позволяет избежать разрушительного эффекта слишком высокой силы тока.
Закон Ома может быть выражен в интегральной и дифференциальной формах. В первом случае речь идёт о традиционной формулировке, а его выражение в дифференциальной форме учитывает удельную проводимость – величину, обратную удельному сопротивлению.
В заключение следует сказать, что измерение сопротивления осуществляется с помощью специального прибора — омметра. Но в работающей цепи это сделать невозможно. Определить величину сопротивления без отключения цепи можно расчетным путем используя закон Ома и предварительно измерив напряжение и силу тока на нужном участке цепи.
Нелинейные элементы и цепи
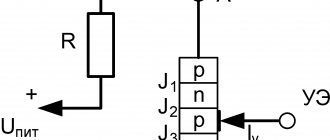
Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ). К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.
Похожие статьи: Постоянный ток. Переменный ток.
Замечания и предложения принимаются и приветствуются!
Формулировка для полной цепи
Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.
Схема с подключенным с источником
Учитывая «r» ЭДС, формула предстанет в следующем виде:
Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.
Напряжение будет меньше ЭДС, определить его можно по формуле:
Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.
Принятые единицы измерения
Необходимо учитывать, что все расчеты должны проводиться в следующих единицах измерения:
- напряжение – в вольтах;
- ток в амперах
- сопротивление в омах.
Если вам встречаются другие величины, то их необходимо будет перевести к общепринятым.
Сила тока I
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.
Напряжение U, или разность потенциалов
Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Сопротивление R
Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Памятник Георгу Симону Ому