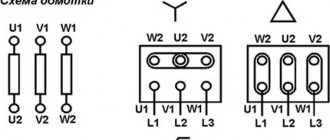
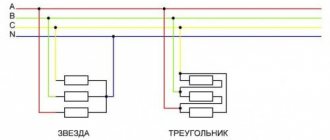
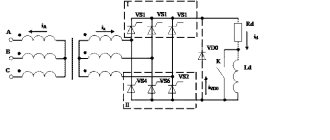
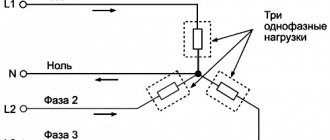
Трехфазная нагрузка, соединенная по схеме «звезда»
Если нагрузки (приемники) соединены в трехфазную цепь по схеме «звезда» (рис.1), то к сопротивлениям нагрузки приложены фазные напряжения. Линейные токи равны фазным и определяются по закону Ома:
а ток в нейтрали равен векторной сумме этих токов: IN
=
IA
+
IB
+
IC
.
Рис.1
При симметричных напряжениях UA
,
UB
,
UC
и одинаковых сопротивлениях
RA
=
RB
=
RC
=
R
токи
IA
,
IB
,
IC
также симметричны и их векторная сумма (
IN
) равна нулю. Тогда
IЛ =
IФ
=
UԤR
;
IN
= 0.
Если же сопротивления фаз нагрузки неодинаковы, то через нулевой провод протекает некоторый ток IN
¹ 0. Это поясняется на векторных диаграммах (рис.2).
Рис.2.
Мощность трёхфазной нагрузки складывается из мощностей фаз: SP =
PА +PВ +PС.
Когда нагрузка симметричная и чисто резистивная, имеем
SP = 3
PФ
=
3UФ×IФ
.
При смешанной (активно-индуктивной или активно-емкостной) нагрузке:
Активная мощность
SP = 3
×UФ×IФ×cosj =Ö3×UЛ×IЛ×cosj
.
Реактивная мощность
SQ = 3
×UФ×IФ×sinj
=
Ö3×UЛ×IЛ×sinj
.
Полная мощность
SS = 3
×UФIФ =Ö3×UЛ×IЛ
.
Расчет трехфазной цепи, соединенной звездой
Соединение в треугольник. Схема, определения
Соединение в звезду. Схема, определения
Если концы всех фаз генератора соединить в общий узел, а начала фаз соединить с нагрузкой, образующей трехлучевую звезду сопротивлений, получится трехфазная цепь, соединенная звездой. При этом три обратных провода сливаются в один, называемый нулевым или нейтральным. Трехфазная цепь, соединенная звездой, изображена на рис. 7. 1.
Рис. 7.1
Провода, идущие от источника к нагрузке называют линейными проводами, провод, соединяющий нейтральные точки источника Nи приемника N’ называют нейтральным (нулевым) проводом.
Напряжения между началами фаз или между линейными проводами называют линейными напряжениями. Напряжения между началом и концом фазы или между линейным и нейтральным проводами называются фазными напряжениями.
Токи в фазах приемника или источника называют фазными токами, токи в линейных проводах — линейными токами. Так как линейные провода соединены последовательно с фазами источника и приемника, линейные токи при соединении звездой являются одновременно фазными токами.
Iл = Iф.
ZN — сопротивление нейтрального провода.
Линейные напряжения равны геометрическим разностям соответствующих фазных напряжений
(7.1)
На рис. 7.2 изображена векторная диаграмма фазных и линейных напряжений симметричного источника.
Рис. 7.2
Из векторной диаграммы видно, что
При симметричной системе ЭДС источника линейное напряжение больше фазного в √3 раз.
Uл = √3 Uф
Если конец каждой фазы обмотки генератора соединить с началом следующей фазы, образуется соединение в треугольник. К точкам соединений обмоток подключают три линейных провода, ведущие к нагрузке. На рис. 7.3 изображена трехфазная цепь, соединенная треугольником. Как видно из рис. 7.3, в трехфазной цепи, соединенной треугольником, фазные и линейные напряжения одинаковы.
Uл = Uф
IA, IB, IC — линейные токи;
Iab, Ibc, Ica- фазные токи.
Линейные и фазные токи нагрузки связаны между собой первым законом Кирхгофа для узлов а, b, с.
Рис. 7.3
Линейный ток равен геометрической разности соответствующих фазных токов. На рис. 7.4 изображена векторная диаграмма трехфазной цепи, соединенной треугольником при симметричной нагрузке. Нагрузка является симметричной, если сопротивления фаз одинаковы. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений, так как нагрузка состоит из активных сопротивлений.
Рис. 7.4
Из векторной диаграммы видно, что
,
Iл = √3 Iф при симметричной нагрузке.
Трехфазные цепи, соединенные звездой, получили большее распространение, чем трехфазные цепи, соединенные треугольником. Это объясняется тем, что, во-первых, в цепи, соединенной звездой, можно получить два напряжения: линейное и фазное. Во-вторых, если фазы обмотки электрической машины, соединенной треугольником, находятся в неодинаковых условиях, в обмотке появляются дополнительные токи, нагружающие ее. Такие токи отсутствуют в фазах электрической машины, соединенных по схеме «звезда». Поэтому на практике избегают соединять обмотки трехфазных электрических машин в треугольник.
Трехфазную цепь, соединенную звездой, удобнее всего рассчитать методом двух узлов. На рис. 7.5 изображена трехфазная цепь при соединении звездой. В общем случае сопротивления фаз нагрузки неодинаковы (ZA ≠ ZB ≠ ZC )
Нейтральный провод имеет конечное сопротивление ZN . В схеме между нейтральными точками источника и нагрузки возникает узловое напряжение или напряжение смещения нейтрали. Это напряжение определяется по формуле (7.2).
Рис.7.5
(7.2)
Фазные токи определяются по формулам (в соответствии с законом Ома для активной ветви):
(7.3)
Ток в нейтральном проводе
(7.4)
Частные случаи.
1. Симметричная нагрузка. Сопротивления фаз нагрузки одинаковы и равны некоторому активному сопротивлению ZA = ZB = ZC = R. Узловое напряжение
,
потому что трехфазная система ЭДС симметрична, .
Напряжения фаз нагрузки и генератора одинаковы:
Фазные токи одинаковы по величине и совпадают по фазе со своими фазными напряжениями. Ток в нейтральном проводе отсутствует
В трехфазной системе, соединенной звездой, при симметричной нагрузке нейтральный провод не нужен.
На рис. 7.6 изображена векторная диаграмма трехфазной цепи для симметричной нагрузки.
2. Нагрузка несимметричная, RA< RB = RC, но сопротивление нейтрального провода равно нулю: ZN = 0. Напряжение смещения нейтрали
рис. 7.6
Фазные напряжения нагрузки и генератора одинаковы
Фазные токи определяются по формулам
Вектор тока в нейтральном проводе равен геометрической сумме векторов фазных токов.
На рис. 7.7 приведена векторная диаграмма трехфазной цепи, соединенной звездой, с нейтральным проводом, имеющим нулевое сопротивление, нагрузкой которой являются неодинаковые по величине активные сопротивления.
Рис. 7.7
3. Нагрузка несимметричная, RA< RB = RC, нейтральный провод отсутствует,
В схеме появляется напряжение смещения нейтрали, вычисляемое по формуле:
Система фазных напряжений генератора остается симметричной. Это объясняется тем, что источник трехфазных ЭДС имеет практически бесконечно большую мощность. Несимметрия нагрузки не влияет на систему напряжений генератора. Из-за напряжения смещения нейтрали фазные напряжения нагрузки становятся неодинаковыми. Фазные напряжения генератора и нагрузки отличаются друг от друга. При отсутствии нейтрального провода геометрическая сумма фазных токов равна нулю.
На рис. 7.8 изображена векторная диаграмма трехфазной цепи с несимметричной нагрузкой и оборванным нейтральным проводом. Векторы фазных токов совпадают по направлению с векторами соответствующих фазных напряжений нагрузки. Нейтральный провод с нулевым сопротивлением в схеме с несимметричной нагрузкой выравнивает несимметрию фазных напряжений нагрузки, т.е. с включением данного нейтрального провода фазные напряжения нагрузки становятся одинаковыми. Рис. 7.8
Аварийные режимы трёхфазной цепи при соединении нагрузки в звезду
Аварийными являются режимы, возникают при коротких замыканиях в нагрузке или в линиях и обрыве проводов. Остановимся на некоторых типичных аварийных режимах.
Обрыв нейтрального провода при несимметричной нагрузке
В симметричном режиме IN
= 0, поэтому обрыв нейтрального провода не приводит к изменению токов и напряжений в цепи и такой режим не является аварийным. Однако, при несимметричной нагрузке
IN
¹ 0, поэтому обрыв нейтрали приводит к изменению всех фазных токов и напряжений. На векторной диаграмме напряжений точка «0» нагрузки, совпадающая до этого с точкой «
N
» генератора, смещается таким образом, чтобы сумма фазных токов оказалась равной нулю (рис.3). Напряжения на отдельных фазах могут существенно превысить номинальное напряжение.
Рис. 3.
Обрыв фазы при симметричной нагрузке в схеме с нулевым проводом
При обрыве провода, например, в фазе А ток этой фазы становится равным нулю, напряжения и токи в фазах В и С не изменяются, а в нулевом проводе появляется ток
IN =
IB +IC.
Он равен току, который до обрыва протекал в фазе А (рис. 4).
Рис.4
Обрыв фазы при симметричной нагрузке в схеме без нулевого провода
При обрыве, например, фазы А сопротивления RA и RB оказываются соединёнными последовательно и к ним приложено линейное напряжение UBC. Напряжение на каждом из сопротивлений составляет от фазного напряжения в нормальном режиме. Нулевая точка нагрузки на векторной диаграмме напряжений смещается на линию ВС и при RB = RC находится точно в середине отрезка ВС (рис.5)
Рис.5
Короткое замыкание в цепи, питающейся от шин неизменного напряжения
На рис.1 показана простая симметричная трехфазная цепь с активноиндуктивным сопротивлением, что характерно для большинства реальных электрических сетей. Цепь питается от источника, у которого в нормальном режиме работы и при КЗ на зажимах сохраняется симметричная и неизменная по значению трехфазная система напряжений. Векторная диаграмма рассматриваемой цепи для нормального режима работы показана на рис.2,а. Угол φ между током и напряжением каждой фазы определяется соотношением активных и индуктивных сопротивлений всей цепи, включая нагрузку.
Рис.1. Трехфазная симметричная цепь, питаемая от шин неизменного напряжения (от источника бесконечной мощности)
Рис.2. Векторные диаграммы токов и напряжений: а — в нормальном режиме; б — при трехфазном коротком замыкании
Короткое замыкание делит цепь на две части: правую с сопротивлениями r1 и x1 = ωL1 в каждой фазе и левую, содержащую источник питания и сопротивления цепи КЗ rK и xK = ωLK. Процессы в обеих частях схемы при трехфазном КЗ протекают независимо.
Правая часть рассматриваемой цепи оказывается зашунтированной КЗ, и ток в ней будет поддерживаться лишь до тех пор, пока запасенная в индуктивности L1 энергия магнитного поля не перейдет в тепло, выделяющееся в активном сопротивлении r1. Этот ток при активно-индуктивном характере сопротивления цепи не превышает тока нормального режима и, постепенно затухая до нуля, не представляет опасности для оборудования.
Изменение режима в левой части цепи, содержащей источник питания, при наличии индуктивности LK также сопровождается переходным процессом. Из курса «Теоретические основы электротехники» известно уравнение, описывающее этот процесс:
(1)
где u и i — соответственно мгновенные значения напряжения и тока рассматриваемой фазы.
Решение этого уравнения дает выражение для мгновенного значения тока в любой момент времени t от начала КЗ:
(2)
где Um — амплитудное значение фазного напряжения источника; ZK — полное сопротивление присоединенного к источнику участка цепи (цепи КЗ); α — фазовый угол напряжения источника в момент t = 0; φK — угол сдвига тока в цепи КЗ относительно напряжения источника той же фазы; Тa — постоянная времени цепи КЗ:
(3)
Как видно из (2), полный ток КЗ слагается из двух составляющих: вынужденной, обусловленной действием напряжения источника (первый член в правой части уравнения), и свободной, обусловленной изменением запаса энергии магнитного поля в индуктивности LK (второй член уравнения).
Вынужденная составляющая тока КЗ имеет периодический характер с частотой, равной частоте напряжения источника. Называют эту составляющую обычно периодической составляющей тока КЗ
(4)
где Iп,m — амплитудное значение периодической составляющей тока.
Угол сдвига φK между векторами тока и напряжения определяется соотношением активных и индуктивных сопротивлений цепи КЗ. Для реальных цепей обычно хK » rK и φK = 45-90°. Векторная диаграмма для периодической составляющей КЗ при φK = 90° показана на рис.2,б. Свободная составляющая тока
(5)
имеет апериодический характер изменения, на основании чего эту составляющую тока называют также апериодической составляющей тока КЗ.
Начальное значение апериодической составляющей тока КЗ в каждой фазе определится по выражению (2) для момента времени t=0:
(6)
здесь iK,0 — начальное значение тока КЗ, которое с учетом невозможности изменения тока скачком в цепи с индуктивностью равно i(0) — току предшествующего режима в данной фазе к моменту t=0. Значение периодической составляющей тока при t=0 определится как
(7)
Представляют определенный интерес условия возникновения максимально возможного значения полного тока КЗ и его апериодической составляющей. Из (6) и (7) при xK » rK и φK≈90° следует, что максимальное значение тока ia,0 будет в случае, если напряжение в момент возникновения КЗ проходит через нулевое значение (α=0) и тока в цепи до КЗ нет, т.е. i(0)=0. При этом ia,0=Iп,m. Кривая изменения тока при условии максимального значения апериодической составляющей тока показана на рис.4. Здесь ia,0=Iп,m.
Рис.3. Изменение тока КЗ в цепи, питаемой от шин неизменного напряжения при максимальном значении апериодической составляющей
Максимальное мгновенное значение полного тока наступает обычно через 0,01 с после начала процесса КЗ (рис.3). Оно носит название ударного тока и обозначается iy. Ударный ток определится из (2) для момента времени t=0,01с:
(8)
или
(9)
где ky — ударный коэффициент, зависящий от постоянной времени цепи КЗ:
(10)
Переходный процесс в случае питания от шин неизменного напряжения завершается после затухания апериодической составляющей тока, и далее полный ток КЗ равен его периодической составляющей, неизменной по амплитуде.
Действующее значение тока для произвольного момента времени КЗ t равно:
периодической составляющей
(11)
апериодической составляющей
(12)
полного тока КЗ
(13)
Добавить ссылку на обсуждение статьи на форуме
РадиоКот >Статьи >
| Теги статьи: | Добавить тег |
Трехфазные цепи или в чем отличие фазы от ноля?
Автор: Atomik Опубликовано 04.10.2006
Понятия ФАЗА
и
НОЛЬ
вытекают из темы
ТРЕХФАЗНЫЕ
(в дальнейшем —
3Ф
)
ЦЕПИ
, потому рассмотрим их подробно.
Что это такое вообще? А вот что: Если соединить несколько однофазных цепей (состоят из генератора, нагрузки и двух проводов линии: прямого и обратного), токи в которых имеют одну частоту, но сдвинуты относительно друг друга по фазе, то можно получить такое условие, когда сумма токов в обратных проводах будет равна нулю. Тогда можем объединить все обратные провода в один и отказаться от них, тем самым сэкономив на материале провода (можно купить еще вискаса!(К черту вискас — осетрину давай! Здесь и далее прим. Кота.
)). Эта возможность и дала основание для распространения многофазных цепей, в частности при производстве и передаче электроэнергии применяются почти исключительно 3Ф цепи. Кстати, все основные звенья 3Ф цепей (3Ф генератор, 3Ф трансформатор и 3Ф двигатель) были разработаны русским инженером Доливо-Добровольским еще в 1880-е годы! Причина распространения 3Ф систем также в том, что 3Ф генератор, 3Ф трансформатор и 3Ф двигатель наиболее просты по конструкции, экономичны и надежны в работе по сравнению с другими.
3Ф система электрических цепей — совокупность трех однофазных цепей, в которых действует ЭДС одной и той же частоты, но сдвинуты на угол 120° одна от другой. Отдельную цепь из этих трех называют ФАЗА. ФАЗА, это участок, по оторому течет один и тот же ток.
3Ф система ЭДС является симметричной, если эти ЭДС сдвинуты относительно друг друга на 120° и имеют равные амплитуды. 3Ф генераторы на электростанциях создают именно симметричную систему ЭДС.
3Ф нагрузка является симметричной, если комплексные сопротивления всех трех ее ФАЗ равны. Если к симметричной нагрузке приложена симметричная система ЭДС, будет иметь место 3Ф симметричная система токов.
Одни выводы фазных обмоток генератора условно называют начала и обозначают на схемах ABC, а другие — концы и обозначают XYZ.
Порядок, в котором ЭДС фаз генератора проходят через одинаковые значения называется чередования фаз.
Сумма ЭДС симметричной системы в любой момент времени равна 0.
Способов соединения ФАЗ в 3Ф цепях два: треугольником и звездой. Соединение звезда, это соединение, при котором концы XYZ фазных обмоток генератора соединяют в общий узел, называемый НЕЙТРАЛЬНАЯ или НУЛЕВАЯ точка генератора (N или O). Соединение звездой показано на рисунке №1. Соединение ФАЗ генератора в звезду:
Соединение ФАЗ генератора в треугольник, это такое соединение, при котором начало одной ФАЗЫ было соединено с концом следующей.
При отсутствии нагрузки, (т.е. при разомкнутых выводах генератора) в обмотках генератора, соединенных в треугольник, ток не течет т.к. сумма симметричных ЭДС дает «0». Исходя из этого возможно только четыре соединения генератора с приемником: 1. треугольник — треугольник 2. треугольник — звезда 3. звезда — треугольник 4. звезда — звезда
Но, это было бы правдой, если бы не нейтральная (нулевая) точка, возникающая при соединении звездой. Ведь средние точки можно тоже соединить. Получаем еще один способ: 5. звезда — звезда, с нейтралью. (Y+Yn) Он-то нам и нужен! Вот это соединение:
Тут я много чего понаписал, объясняю:
Комплексное (с точкой) Ua, Ub, Uc — фазные напряжения. Комплексное Uab, Ubc, Uca — линейные напряжения. Комплексный Ia, Ib, Ic — Линейные токи (показывают от генератора к приемнику). Комплексное In — показывают от приемника к генератору, по сути нейтраль (тот самый НОЛЬ в розетке) является обратным проводом.
А теперь самое интересное (в свое время меня поразило) По второму закону Кирхгофа:
Uab = Ua — Ub Ubc = Ub — Uc Uca = Uc — Ua
Из этого следует, что:
Uab + Ubc + Uca = 0 ! (в симметричном режиме)
По первому закону Кирхгофа:
Ia + Ib + Ic = In
В симметричном режиме In = 0
Следовательно в симметричном режиме нейтраль не нужна!
Если внимательно рассмотреть векторную диаграмму, представленную на рисунке, то станет ясен вопрос, который тревожит очень многих: почему именно 220В, а не 200 или 250 и т.д. Или в общем виде: «почему шкала стандартных напряжений приемников выглядит, как 127, 220, 380, 660». А вот почему. Посмотрим снова на рисунок №4, что мы видим? Рассмотрим вектор напряжения Uab. Uab = Ua*cos30° + Ub*cos30° = 2 Uф*cos30° = sqrt3*Uф Uл = sqrt3*Uф
Uф
, это разность потенциалов между проводом линии и нейтралью.
Uл
, это Напряжение между двумя линейными проводами (межфазное).
Теперь возьмем, к примеру, 220 вольт как Uф, вычисляя Uл получим 381,05 Вольт Возьмем эти за Uф 381,05 и снова вычислим, получим 659,99 вольт. И так далее. Вот откуда эти мистические цифры — из углов сдвига ФАЗ и математики! Итак, при симметричной нагрузке нейтраль не нужна, так, как тока в ней все равно не будет. Тогда 3Ф система буде трехпроводной, что дает экономию на материале 50% по сравнению с однофазной (при одной и той же передаваемой мощности). На практике 3Ф нагрузка встречается (3Ф двигатель), однако даже в такой 3Ф цепи все равно возможен несиметричный режим, который, к примеру может быть вызван обрывом одной из фаз, или там несимметричный КЗ (между двумя фазами). При несимметричной нагрузке и отсутствии нейтрали потенциал нейтральной точки нагрузки не будет равен нулю. Его можно определить по методу двух узлов находя смещение нейтрали:
Из схемы без нейтрали (рисунок №-1) видно, что в соответствии со вторым законом Кирхгофа фазные напряжения не будут равны ЭДС истояника на величину смещения нейтрали.
ВД для несимметричного режима без нейтрали:
При отсутствии нейтрали нарушается симметрия фазных напряжений. При любом изменении в одной из фаз точка n будет двигаться по плоскости перетаскивая за собой вектора фазных напряжений. Короче — дело дрянь. По этому поводу мне как-то сказали: хочешь увидеть фейерверк — перережь нейтральный провод в доме напротив  В результате при изменении нагрузки только одной из фаз изменяются все три фазных непряжения. Работа фаз не будет назависимой, это недопустимо, так как потребители, вкдюченные в разные фазы рассчитаны на работу при определенном Uф.
В результате при изменении нагрузки только одной из фаз изменяются все три фазных непряжения. Работа фаз не будет назависимой, это недопустимо, так как потребители, вкдюченные в разные фазы рассчитаны на работу при определенном Uф.
Для устранения такой зависимости одной фазы от другой, т.е. для обеспечения симметрии фазных напряжений при несимметричной нагрузке и предназначен нейтральный провод.
Несмотря на отсутствие разности потенциалов на нейтрали по ней будет протекать ток, вызванный несимметрией нагрузки. Короче «лишний ток» стекает по нейтрали. Почему нейтраль называют землей? Потому, что на электростанции нулевая точка генератора заземлена, т.е. буквально провод закопан в землю. Это сделано для страховки. Ну, а если кого-то заинтересует вопрос: «Как же это все работает на практике?», то вот упрощенная схема питания наших с вами квартир от электростанции.
От 3Ф генератора энергия идет к 3Ф трансформатору (тот, что у нас на подстанции) а от него уже поступает к нам в розетки на стене (на схеме потребители обозначены символом резисторов и подписаны, как 3Ф нагрузка)
И в завершение, пройдемся по главному из данной темы. Итак, выводы: а)
ФАЗА и НОЛЬ совершенно разные вещи! (Теперь мы знаем, что НОЛЬ, в общем может быть и не нужен, соединим все обратные провода из розеток по три штуки в одну точку и все, главное, чтоб нагрузка симметричная была, но вот ФАЗА нужна обязательно… Значит различия все-таки есть 
б)
ФАЗА фактически есть участок, по которому течет один и тот же ток. В розетке, же, на стене, это провод по которому ток к нам идет от генератора. (в отличие от НОЛЯ по которому тот стекает обратно к генератору, в его нулевую точку) Можно также сказать, что это один из трех переменных токов, вырабатываемых 3Ф генератором.
в)
НОЛЬ (он же нейтраль) фактически есть провод, соединяющий нулевую точку генератора и нулевую точку нагрузки.
г)
НОЛЬ буквально заземлен, но на электростанции.
д)
Преимущество схемы YN в том, что она дает возможность подключения на 2 напряжения: между двумя линейными проводами и между фазой и нейтралью. ТАД (3Ф асинхронный двигатель U1 = 380/220)
е)
При соединении фаз нагрузки в треугольник, каждая фаза находится под линейным напряжением, а при соединении в звезду под напряжением в раз меньше.
ж)
При любой схеме соединения, в случае симметричного режима расчет 3Ф цепи сводится к расчету одной из фаз.
з)
На практике указывают линейные напряжения и токи, поскольку не всегда есть доступ для приборов к нейтральной точке приемника.
Это все основные моменты о 3Ф цепях. Есть, что добавить? Пишите.
Вопросы, как обычно, складываем тут.
| Как вам эта статья? | Заработало ли это устройство у вас? | |
| 38 | 0 | 0 |
| 1 | 1 |
§60. Схема соединения «звездой»
Схема «звезда с нулевым проводом».
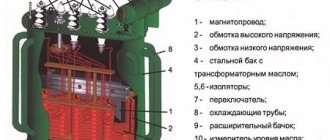
При соединении фазных обмоток источника трехфазного тока (например, генератора) по схеме «звезда с нулевым проводом» концы его трех обмоток соединяют в общий узел 0, который называется нулевой точкой, или нейтралью источника (рис. 206).
Рис. 206. Схема «звезда с нулевым проводом», направление в ней линейных и фазных токов и напряжений
Приемники электрической энергии объединяют в три группы ZA, ZB и Zc (фазы нагрузки), концы которых также соединяют в общий узел 0′ (нулевая точка, или нейтраль нагрузки). Обмотки источника соединяют с фазами нагрузки четырьмя проводами. Провода 1, 2 и 3, присоединенные к началам фазных обмоток (А, В, С), называют линейными. Провод 4, соединяющий нулевые точки 0 и 0′, называют нулевым, или нейтральным.
Напряжения uА, uв и uс между началами и концами обмоток отдельных фаз источника или фаз нагрузки ZA, ZB и Zc называют фазными. Они равны также напряжениям между каждым из линейных проводов и нулевым проводом. При отсутствии потери напряжения в обмотках источника (при холостом ходе) фазные напряжения равны соответствующим э. д. с. в этих обмотках.
Фазными токами iA, iB, ic называют токи, протекающие по обмоткам источника или фазам нагрузки ZA, ZB и Zc. Напряжения uAB, uBC, uCA между линейными проводами и токи, проходящие по этим проводам, называют линейными.
Примем условно за положительное направление токов iA, iB и ic в фазах источника — от конца соответствующей фазы к ее началу,в фазах нагрузки — от начала к концу, а в линейных проводах — от источника к приемнику.
Будем считать положительными напряжения uА, uB и uC в фазах источника и нагрузки, если они направлены от начала фаз к концам, а линейные напряжения uАВ, uBC, uСА — если они направлены от предыдущей фазы к последующей.
Из рис. 206 следует, что в схеме «звезда» линейные токи равны фазным, т. е. Iл = Iф, так как при переходе от фазы источника или нагрузки к линейному проводу нет каких-либо ответвлений.
Мгновенные значения напряжений согласно второму закону Кирхгофа:
uАВ = uА – uB; uBC = uB – uС; uСА = uС – uА.
Переходя от мгновенных значений напряжений к их векторам, имеем:
Следовательно, линейное напряжение равно разности векторов соответствующих фазных напряжений.
По полученным векторным уравнениям можно построить векторную диаграмму (рис. 207, а), которую можно преобразовать в диаграмму (рис. 207,б). Из этой диаграммы видно, что в симметричной трехфазной системе векторы линейных напряжений →uAB, →uВС, →uСА образуют равносторонний треугольник ABC, внутри которого расположена симметричная трехлучевая звезда фазных напряжений →uА, →uВ, →uС.
В равнобедренных треугольниках АОВ, ВОС и СОА основание равно Uл две другие стороны — Uф и острый угол между этими сторонами и основанием составляет 30°.
Рис. 207. Векторные диаграммы напряжений для схемы «звезда с нулевым проводом»
Следовательно,
Uл = 2Uф cos 30° = 2Uф (√3)/2 = √3 Uф
Таким образом, в трехфазной системе, соединенной по схеме «звезда с нулевым проводом», линейное напряжение больше фазного в √З раз. Величина √З = 1,73 положена в основу шкалы номинальных напряжений переменного тока: 127, 220, 380 и 660 В. В этом ряду каждое следующее значение напряжения больше предыдущего в 1,73 раза.
В нулевом проводе проходит ток i0, мгновенное значение которого равно алгебраической сумме мгновенных значений токов, проходящих в отдельных фазах: i0 = iA+iB+iC.
Переходя от мгновенных значений токов к их векторам, имеем:
→i0=→iA+→iB+→iC.
Векторы токов →iА, →iВ и →iС сдвинуты относительно векторов соответствующих напряжений →uA, →uB, →uС на углы →iA, →iB, →iC (рис. 208, а). Значения этих углов зависят от соотношения между активным и реактивным сопротивлениями, включенными в данную фазу.
На этой же диаграмме показано сложение векторов →iА, →iВ и →iC для определения вектора тока →i0. Обычно ток →i0 меньше токов
Рис. 208. Векторные диаграммы напряжений и токов в отдельных фазах для схемы «звезда с нулевым проводом» при неравномерной (а) и равномерной (б) нагрузках фаз
IA, 1В и IC в линейных проводах, поэтому нулевой провод имеет площадь поперечного сечения, равную или даже несколько меньшую площади сечения линейных проводов.
В схеме «звезда с нулевым проводом» приемники электрической энергии можно включать на два напряжения: линейное Uл (при подключении к двум линейным проводам) и фазное UФ (при подключении к нулевому и одному из линейных проводов).
Схема «звезда без нулевого провода».
При равномерной или симметричной нагрузке всех трех фаз, когда во всех фазах включены одинаковые активные и реактивные сопротивления (RA =RB = RC и ХA=ХВ=ХС), фазные токи iA, iB и iC будут равны по величине и сдвинуты от соответствующих фазных напряжений на равные углы. В этом случае получаем симметричную систему токов, при которой токи iA, iB, iC будут сдвинуты по фазе друг относительно друга на угол 120°, а ток i0 в нулевом проводе в любой момент времени равен нулю (рис. 208,б).
Очевидно, что при равномерной нагрузке можно удалить нулевой провод и передавать электрическую энергию источника к приемнику по трем линейным проводам 1, 2 и 3 (рис. 209).
Рис. 209. Схема «звезда без нулевого провода»
Такая схема называется «звезда без нулевого провода». При трехпроводной системе передачи электрической энергии в каждое мгновение ток по одному (или двум) проводу проходит от источника трехфазного тока к приемнику, а по двум другим (или одному) протекает обратно от приемника к источнику (рис. 210).
Рис 210. Кривые изменения токов в линейных проводах (а) при трехпроводной системе и направление в них токов в различные моменты времени (б в, г)
Векторная диаграмма напряжений для схемы «звезда без нулевого провода» при равномерной нагрузке фаз будет такая же, как и для схемы «звезда с нулевым проводом» (см. рис. 207).
Такими же будут и соотношения между фазными и линейными токами и напряжениями:
Iл = IФ и Uл = √3 UФ
Следует отметить, что схема «звезда без нулевого провода» может быть применена только при равномерной нагрузке фаз. Практически это имеет место лишь при подключении к источникам трехфазного тока электрических двигателей, так как каждый трехфазный электродвигатель снабжен тремя одинаковыми обмотками, которые равномерно нагружают все три фазы.
При неравномерной нагрузке напряжения на отдельных фазах нагрузки будут различными. На некоторых фазах (с меньшим сопротивлением) напряжение уменьшится, а на других увеличится по сравнению с нормальным, что является недопустимым.
Практически неравномерная нагрузка фаз возникает при питании трехфазным током электрических ламп, так как в этом случае распределение тока между всеми тремя фазами не может быть гарантировано (отдельные лампы могут включаться и выключаться в индивидуальном порядке). Особенно опасны в схеме «звезда без нулевого провода» обрыв или короткое замыкание в одной из фаз.
Можно показать путем построения соответствующих векторных диаграмм, что при обрыве в одной из фаз напряжение в других двух фазах уменьшается до половины линейного, вследствие чего лампы, включенные в эти фазы, будут гореть с недокалом.
При коротком замыкании в одной из фаз напряжение в других фазах увеличивается до линейного, т. е. в √З раз, и все лампы, включенные в этих фазах, перегорят. Поэтому при схеме «звезда с нулевым проводом» во избежание разрыва цепи нулевого провода в ней не устанавливают предохранители и выключатели.