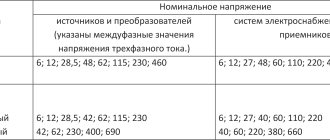
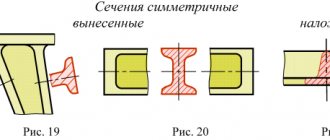
При расчете любых электрических сетей используется такое понятие, как площадь поперечного сечения проводника. Это свойство напрямую влияет на безопасность и долговечность всей системы, поэтому важно, чтобы расчетное значение площади поперечного сечения электрического проводника соответствовало фактическому. В данной статье будут рассмотрены способы измерения диаметра проводника и его сечения, а также рассмотрены другие варианты определения характеристик провода.
Способы измерения диаметра провода
Для того, чтобы рассчитать площадь поперечного сечения проводника необходимо знать его точный диаметр. Существует несколько способов измерения диаметра провода. К ним относятся измерения:
- При помощи штангенциркуля: для этого нужно понимать принцип работы штангенциркуля и уметь снимать показания с его шкал. В этом случае упростить измерения позволяет использование электронного измерительного прибора – он покажет точное значение диаметра на своем экране.
- С использованием микрометра: показания данного прибора немного точнее, чем у механического штангенциркуля, но он также требует некоторых навыков для снятия правильных и точных показаний.
- С помощью обычной линейки: данный способ подходит тем, кто не имеет в своем арсенале таких измерительных приборов, как штангенциркуль или микрометр. Измерение диаметра проводника с использованием линейки не будет достаточно точным, но примерно оценить диаметр будет возможно.
Для измерения диаметра проводника в первую очередь его зачищают ножом или стриппером от изоляции. Далее, если используется микрометр или штангенциркуль, жилу провода плотно зажимают между губок прибора и определяют размер проводника по шкалам устройства. При использовании линейки изоляция снимается на расстояние 5-10 см и жила наматывается на отвертку. Витки проводника должны плотно прижиматься друг к другу (ориентировочно 8-20 витков). Далее измеряется длина намотанного участка и полученное значение делится на количество витков – получится более или менее точное значение диаметра.
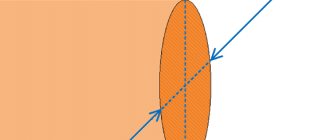
Стереометрия. Площадь сечения через площадь проекции сечения.
Если сечение сложной формы, то не стоит пытаться найти его площадь “в лоб”. Умный гору обойдет… И мы обойдем: определим площадь проекции сечения (обычно это очень просто) и угол наклона плоскости сечения к плоскости основания. Потом воспользуемся известной формулой. Но об этом – дальше.
Задача 1. В прямоугольном параллелепипеде с ребрами ‚ и точки и -середины ребер и соответственно. Плоскость пересекает ребро в точке .
а) Докажите, что ;
б) Найдите площадь сечения этого параллелепипеда плоскостью .
Рисунок 1 – к задаче 1
Построим сечение. Построим прямую – ведь точки и принадлежат одной грани. Построим прямую и найдем точку пересечения прямой и прямой – точку .
Рисунок 2 – к задаче 1
Эта точка принадлежит как плоскости грани , так и плоскости грани . Проведем прямую и определим точку пересечения этой прямой с ребром – точку .
Рисунок 3 – к задаче 1
Построим линии, по которым сечение «режет» грани параллелепипеда: .
Рисунок 4 – к задаче 1
Теперь построим прямую и определим точку ее пересечения с прямой – точка пересечения лежит в плоскости верхней грани, и это позволяет соединить ее с точкой . Теперь найдем место пересечения отрезка с ребром – точку , и можно обводить и штриховать сечение:
Рисунок 5 – к задаче 1
Докажем пункт а). Рассмотрим треугольники и . Они подобны, так как образованы параллельными прямыми: . Так как , то коэффициент подобия этих треугольников – . Тогда . Так как треугольники и также подобны с коэффициентом , то . Но треугольники и равны по 2 признаку, следовательно, , или , то есть .
б) Определим площадь сечения. Для этого можно определить площадь проекции этого сечения, и косинус угла между плоскостью и основанием параллелепипеда. Сначала найдем площадь проекции. Отрежем два треугольника от основания параллелепипеда, тогда оставшееся – и есть площадь проекции (многоугольник – выделено голубым цветом).
Рисунок 6 – к задаче 1
Площадь основания параллелепипеда равна 12, отрезаем треугольник : по условию, по доказанному отношению из пункта а). Следовательно,
Отрезаем треугольник : по условию, по доказанному отношению из пункта а). Следовательно,
Тогда площадь проекции равна
Теперь найдем угол наклона плоскости сечения к плоскости основания, вернее, его косинус. Нужно найти косинус угла – или любую другую тригонометрическую функцию – угла . Рассмотрим треугольник . Он прямоугольный, катет (равен высоте параллелепипеда). Длина отрезка может быть найдена из треугольника :
По ранее доказанному , .
Тогда
Площадь сечения равна
Ответ: .
Задача 2. В правильной четырехугольной призме сторона основания равна 6, а боковое ребро равно . На ребрах и отмечены точки и соответственно, причем .
а) Пусть – точка пересечения плоскости с ребром . Докажите, что – квадрат;
б) Найдите площадь сечения призмы плоскостью .
Рисунок 1 – к задаче 2
Проведем прямую и через точку – параллельную ей прямую, так как плоскость сечет противоположные грани параллелепипеда (прямой призмы) по параллельным прямым:
Рисунок 2 – к задаче 2
Найдем точку пересечения прямой и – точку . Эта точка принадлежит плоскости грани . Поэтому ее можно соединить с точкой отрезком, который пересечет ребро в точке . Найдем точку пересечения прямой и – точку . Эта точка принадлежит плоскости грани . Поэтому ее можно соединить с точкой отрезком, который пересечет ребро в точке .
Рисунок 3 – к задаче 2
Рисунок 4 – к задаче 2
Соединяя точки , , , , , , получим искомое сечение.
Докажем, что – квадрат.
Рисунок 5 – к задаче 2
Так как отрезки и принадлежат одной плоскости (плоскости сечения) и одновременно параллельным плоскостям верхнего и нижнего оснований призмы, то они параллельны. Также .
и – диагонали прямых правильных призм со стороной основания 1 и высотой . Тогда
Получается, – как минимум, ромб. И по признаку параллелограмма, так как противоположные стороны попарно равны, то – квадрат.
б) Определим площадь сечения. Для этого можно определить площадь проекции этого сечения, и косинус угла между плоскостью и основанием параллелепипеда. Сначала найдем площадь проекции. Отрежем два треугольника от основания параллелепипеда, тогда оставшееся – и есть площадь проекции (многоугольник – выделено фиолетовым цветом).
Рисунок 6 – к задаче 2
Площадь основания призмы равна 36, отрезаем треугольник : по условию, по доказанному отношению из пункта а). Следовательно,
Отрезаем треугольник : по условию, по доказанному отношению из пункта а). Следовательно,
Тогда площадь проекции равна
Теперь найдем угол наклона плоскости сечения к плоскости основания, вернее, его косинус. Нужно найти косинус угла – или любую другую тригонометрическую функцию – угла . Рассмотрим треугольник . Он прямоугольный, катет (равен высоте параллелепипеда). Длина отрезка может быть найдена из треугольника :
По ранее доказанному , .
Тогда
Площадь сечения равна
Ответ: .
Как узнать сечение провода по его диаметру для многожильного или сегментного кабеля
Если определение диаметра для одножильного проводника не вызывает никаких проблем, то измерение многожильного или сегментного может вызвать определенные сложности.
Измерение сечения многожильного провода
При определении диаметра жилы данного кабеля нельзя измерять этот размер сразу для всех проволочек жилы: значение получится неточным, так как между жилами имеется пространство. Поэтому данный кабель сначала необходимо зачистить от изоляции, затем распушить многожильный проводник и посчитать количество проволок в жиле. Далее любым способом (штангенциркуль, линейка, микрометр) измеряют диаметр одной жилы и определяют площадь поперечного сечения проволочки. После этого полученное значение умножают на количество проволочек в пучке и получают точный размер имеющегося проводника.
Измерение сегментного проводника
Определение размеров сегментного проводника несколько сложнее, чем измерения круглого одножильного или многожильного кабеля. Для того, чтобы правильно оценить площадь поперечного сечения такого проводника необходимо использовать специальные таблицы. Например, для расчёта площади сечения сегмента алюминиевого проводника определяют высоту и ширину сегмента и используют следующую таблицу:
| Кабель | Площадь сечения сегмента, мм2 | ||||||||
| 35 | 50 | 70 | 95 | 120 | 150 | 185 | 240 | ||
| Трехжильные секторные однопроволочные, 6(10) кВ | выс | 5,5 | 6,4 | 7,6 | 9 | 10,1 | 11,3 | 12,5 | 14,4 |
| шир | 9,2 | 10,5 | 12,5 | 15 | 16,6 | 18,4 | 20,7 | 23,8 | |
| Трехжильные секторные многопроволочные, 6(10) кВ | выс | 6 | 7 | 9 | 10 | 11 | 12 | 13,2 | 15,2 |
| шир | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 25 | |
| Четырехжильные секторные однопроволочные, до 1 кВ | выс | – | 7 | 8,2 | 9,6 | 10,8 | 12 | 13,2 | – |
| шир | – | 10 | 12 | 14,1 | 16 | 18 | 18 | – | |
Таблица с формулами площади круга
| Радиус круга r | |
| Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно | |
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | радиус | |
| 2 | диаметр | |
| 3 | длина окружности | |
| 4 | сторона квадрата вписанного в круг | |
| 5 | сторона квадрата, в который вписан круг | |
| 6 | стороны треугольника | где |
| 7 | сторона равностороннего треугольника | |
| 8 | высота равностороннего треугольника | |
| 9 | боковая сторона и основание равнобедренного треугольника | |
| 10 | стороны при прямом угле треугольника | |
| 11 | боковая сторона и основание равнобедренного треугольника | |
| 12 | боковые стороны равнобедренного треугольника и угол между ними | |
| 13 | стороны прямоугольного треугольника | |
| 14 | сторона и угол при основании треугольника | |
| 15 | сторона равностороннего треугольника | |
| 16 | сторона и угол при основании трапеции | |
| 17 | боковые стороны и диагональ трапеции | где |
| 18 | стороны прямоугольника | |
| 19 | сторона и количество сторон многоугольника | |
| 20 | сторона шестиугольника |
Расчет по формуле
Главный геометрический показатель токопроводящей жилы – её площадь поперечного сечения. От данного размера зависит пропускная способность электрического проводника, а, следовательно, его эксплуатационные характеристики, которые влияют на безопасность и долговечность. Как уже было сказано выше, данный параметр легко определяется после измерения диаметра проводника. Для этого используется формула для определения площади круга:
Готовые таблицы – это отличный способ быстро определить площадь поперечного сечения провода, но, чтобы быть уверенным на сто процентов в полученном значении – лучше проверить и рассчитать самостоятельно.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Калькулятор расчета сечения провода по диаметру
Для быстрого расчета площади поперечного сечения круглого проводника можно использовать специальный калькулятор, который разработан для этих целей и способен быстро и точно рассчитать размер токопроводящей жилы по формуле указанной выше.
При использовании данного онлайн калькулятора необходимо точно измерить диаметр проводника для монолитного проводника или одной из проволочек многожильного провода с помощью штангенциркуля, микрометра или линейки. Для многожильного проводника потребуется дополнительно посчитать количество проволочек.
Порядок расчета
Поскольку главная задача – это найти площадь проходного сечения трубы, основная формула будет несколько видоизменена.
В результате вычисления производятся так:
S=π×(D/2-N)2, где
D – значение внешнего сечения трубы;
N – толщина стенок.
Примите к сведению, что, чем больше знаков в числе π вы подставите в расчеты, тем точнее они будут.
Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число π равным 3,14.
Итак, расчеты выглядят следующим образом:
S=π×(D/2-N)2=3,14×(1/2-0,01)2=0,754 м2.
Что значит поперечное сечение
Перед тем как раскрыть основное понятие, нужно расшифровать значение термина и понять, чем провод отличается от кабеля. Провод является проводником, который используется, чтобы соединить несколько участков электрической цепи. Может иметь одну или много токовых проводящих жильных элементов. Они в свою очередь могут быть голыми, изолированными, одножильными и многожильными.
Площадь среза проводника
Первые используются в воздушных линиях электрических передач. Вторые применяются в электрических устройствах, щитках или шкафах. В быту они находятся внутри электрической проводки.
К сведению! Изолированные и одножильные проводники используются везде, а многожильные применяются там, где нужны изгибы с малым радиусом.
Что собой представляет поперечное сечение
Поперечным сечением называется фигура, которая образуется от проводникового рассечения плоскостью направления. Площадь, которая получена при перпендикулярном разрезе любого вида провода, указывается в квадратных миллиметрах. Это важный параметр для расчета электрической сети.
Особенности электрических проводов
При всём многообразии кабельной продукции и огромном выборе проводов для прокладки электрических сетей существуют правила подбора. Не обязательно учить наизусть все марки кабелей и проводов, нужно уметь читать и расшифровывать их маркировку. Для начала стоит выяснить различие между проводом и кабелем.
Провод – проводник, используемый для соединения двух участков цепи. Может иметь одну или несколько токопроводящих жил. Жилы могут быть:
- голые;
- изолированные;
- одножильные;
- многожильные.
Голые линии применяются там, где прикосновение к токоведущим жилам невозможно. В большинстве случаев они используются для воздушных линий электропередач.
Изоляционное покрытие применяется однослойное или двухслойное. Провода, имеющие два или три проводника в двойной изоляции, путают с кабелем. Путаница происходит из-за того, что изоляция покрывает каждую жилу, а снаружи выполнено общее полимерное или иное покрытие. Такие проводники нашли применение внутри электрических устройств, щитов или шкафов. В быту они скрыты в стене или проложены в специальных каналах.
Изолированная продукция используется повсеместно. В зависимости от степени электробезопасности помещения и места прокладки, выбирается класс изоляции.
Многожильные проводники используются там, где необходимы изгибы малого радиуса при прокладке сложных трасс, где не могут пройти одножильные аналоги. Такой тип тоководов удобно монтировать в кабельных каналах. Одножильные провода в таких условиях изгибать труднее, нужно прикладывать силу, и существует опасность повреждения жилы.
К сведению. Маркировка АППВ 3*2,5 обозначает провод с алюминиевыми жилами, поливинилхлоридной изоляцией, плоский, имеющий разделительное основание. Расшифровку маркировки уточняют в справочной литературе.
По строению кабель – это сколько-то жил, имеющих индивидуальную изоляцию, помещённых в защитный внешний слой из диэлектрического материала. Пространство между сердечниками и оболочкой, для предотвращения слипания, заполняется бумажными лентами, пластмассовыми нитями или кабельной пряжей. Дополнительно изделие может быть усилено бронёй из лент или стальной оплёткой для защиты от механических повреждений.
Таблица соответствия диаметров проводов и их площадь сечения
Проводить расчеты в магазине или на рынке не всегда хочется или есть возможность. Чтобы не тратить время на расчеты или не ошибиться, можно воспользоваться таблицей соответствия диаметров и сечений проводов, в которой есть наиболее распространенные (нормативные) размеры. Ее можно переписать, распечатать и захватить с собой.
| Диаметр проводника | Сечение проводника |
| 0,8 мм | 0,5 мм2 |
| 0,98 мм | 0,75 мм2 |
| 1,13 мм | 1 мм2 |
| 1,38 мм | 1,5 мм2 |
| 1,6 мм | 2,0 мм2 |
| 1,78 мм | 2,5 мм2 |
| 2,26 мм | 4,0 мм2 |
| 2,76 мм | 6,0 мм2 |
| 3,57 мм | 10,0 мм2 |
| 4,51 мм | 16,0 мм2 |
| 5,64 мм | 25,0 мм2 |
Как работать с этой таблицей? Как правило, на кабелях есть маркировка или бирка, на которой указаны его параметры. Там указывается маркировка кабеля, количество жил и их сечение. Например, ВВНГ 2х4. Нас интересуют параметры жилы а это цифры, которые стоят после знака «х». В данном случае заявлено, что есть два проводника, имеющих поперечное сечение 4 мм2. Вот и будем проверять, соответствует ли эта информация действительности.
Как работать с таблицей
Чтобы проверить, проводите измерение диаметра любым из описанных методов, после сверяетесь с таблицей. В ней указано, что при таком сечении в четыре квадратных миллиметра, размер провода должен быть 2,26 мм. Если измерения у вас такие же или очень близкие (погрешность измерений существует, так как приборы неидеальные), все нормально, можно данный кабель покупать.
Заявленные размеры далеко не всегда соответствуют реальным
Но намного чаще фактический диаметр проводников значительно меньше заявленного. Тогда у вас два пути: искать провод другого производителя или взять большего сечения. За него, конечно, придется переплатить, но первый вариант потребует достаточно большого промежутка времени, да и не факт, что вам удастся найти соответствующий ГОСТу кабель.
Второй вариант потребует больше денег, так как цена существенно зависит от заявленного сечения. Хотя, не факт — хороший кабель, сделанный по всем нормам, может стоит еще дороже. Это и понятно — расходы меди, а, часто, и на изоляцию, при соблюдении технологии и стандартов — значительно больше. Потому производители и хитрят, уменьшая диаметр проводов — чтобы снизить цену. Но такая экономия может обернуться бедой. Так что обязательно проводите измерения перед покупкой. Даже и проверенных поставщиков.
И еще: осмотрите и пощупайте изоляцию. Она должна быть толстой, сплошной, иметь одинаковую толщину. Если кроме изменения диаметра еще и с изоляцией проблемы — ищите кабель другого производителя. Вообще, желательно найти продукцию, отвечающую требованиям ГОСТа, а не сделанную по ТУ. В этом случае есть надежда на то, что кабель или провод буде служить долго и без проблем. Сегодня это сделать непросто, но если вы разводите проводку в доме или подключаете электричество от столба, качество очень важно. Потому, стоит, наверное, поискать.
Определение сечения провода розеточных линий
При определении диаметра провода для комнатной проводки считают максимальную нагрузку потребителей, которые могут быть включены одновременно. Ориентируясь на эту мощность, выбирают сечение основных линий, которые идут от счётчика и вводных автоматов к распределительным коробкам. Это те участки, которые будут нести суммарную нагрузку всех подключенных потребителей. Выбирают провод с медными жилами не менее 6 мм2.
Проводники ответвлений от распределительных коробок к розеткам выбираются индивидуально для каждой комнаты. Тут учитываются бытовые электроприборы, которые могут быть присоединены к розетке. Сечение жил подбирается с запасом на один порядок. Это на тот случай, если возникнет необходимость запитать от розетки какой-то строительный инструмент: перфоратор, сварочный инвертор.
Если суммарная мощность потребителей в комнате будет составлять 4 кВт, то проводник с медной жилой, питающий розетку, должен быть сечением 2,5 мм².
Внимание! Сечение токопроводящей жилы должно позволять выдерживать нагрузку по току и во время работы бытовой техники не перегреваться. На практике определяют прибор самой большой мощности и выбирают подходящий диаметр провода относительно характеристик прибора.
В итоге получается, что отводящий проводник с медными жилами на каждую розетку будет иметь сечение 2,5 мм2. Основной провод для разводки берут сечением 6 мм². При этом следует учесть, что весь контур электропроводки выполняют проводами, имеющими жилы из одного материала. Скручивать между собой жилы из меди и алюминия нельзя.