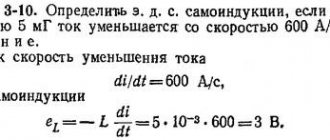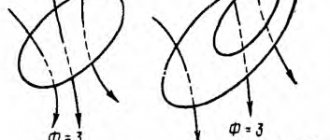Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: самоиндукция, индуктивность, энергия магнитного поля.
Самоиндукция является частным случаем электромагнитной индукции. Оказывается, что электрический ток в контуре, меняющийся со временем, определённым образом воздействует сам на себя.
Ситуация 1
.Предположим, что сила тока в контуре возрастает. Пусть ток течёт против часовой стрелки; тогда магнитное поле этого тока направлено вверх и увеличивается (рис. 1).
Рис. 1. Вихревое поле препятствует увеличению тока
Таким образом, наш контур оказывается в переменном магнитном поле своего собственного тока. Магнитное поле в данном случае возрастает (вместе с током) и потому порождает вихревое электрическое поле, линии которого направлены по часовой стрелке в соответствии с правилом Ленца.
Как видим, вихревое электрическое поле направлено против тока, препятствуя его возрастанию; оно как бы «тормозит» ток. Поэтому при замыкании любой цепи ток устанавливается не мгновенно — требуется некоторое время, чтобы преодолеть тормозящее действие возникающего вихревого электрического поля.
Ситуация 2
. Предположим теперь, что сила тока в контуре уменьшается. Магнитное поле тока также убывает и порождает вихревое электрическое поле, направленное против часовой стрелки (рис. 2).
Рис. 2. Вихревое поле поддерживает убывающий ток
Теперь вихревое электрическое поле направлено в ту же сторону, что и ток; оно поддерживает ток, препятствуя его убыванию.
Как мы знаем, работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура — это ЭДС индукции. Поэтому мы можем дать такое определение.
Явление самоиндукции состоит в том, что при изменении силы тока в контуре возникает ЭДС индукции в этом же самом контуре
.
При возрастании силы тока (в ситуации 1) вихревое электрическое поле совершает отрицательную работу, тормозя свободные заряды. Стало быть, ЭДС индукции в этом случае отрицательна.
При убывании силы тока (в ситуации 2) вихревое электрическое поле совершает положительную работу, «подталкивая» свободные заряды и препятствуя убыванию тока. ЭДС индукции в этом случае также положительна (нетрудно убедиться в том, что знак ЭДС индукции, определённый таким образом, согласуется с правилом выбора знака для ЭДС индукции, сформулированным в листке «Электромагнитная индукция»).
Индуктивность
Мы знаем, что магнитный поток, пронизывающий контур, пропорционален индукции магнитного поля: . Кроме того, опыт показывает, что величина индукции магнитного поля контура с током пропорциональна силе тока: Стало быть, магнитный поток через поверхность контура, создаваемый магнитным полем тока в этом самом контуре, пропорционален силе тока: Коэффициент пропорциональности обозначается и называется индуктивностью контура:
(1)
Индуктивность зависит от геометрических свойств контура (формы и размеров), а также от магнитных свойств среды, в которую помещён контур (Улавливаете аналогию? Ёмкость конденсатора зависит от его геометрических характеристик, а также от диэлектрической проницаемости среды между обкладками конденсатора). Единицей измерения индуктивности служит генри (Гн).
Допустим, что форма контура, его размеры и магнитные свойства среды остаются постоянными (например, наш контур — это катушка, в которую не вводится сердечник); изменение магнитного потока через контур вызвано только изменением силы тока. Тогда , и закон Фарадея приобретает вид:
(2)
Благодаря знаку «минус» в (2) ЭДС индукции оказывается отрицательной при возрастании тока и положительной при убывании тока, что мы и видели выше.
Рассмотрим два опыта, демонстрирующих явление самоиндукции при замыкании и размыкании цепи.
Рис. 3. Самоиндукция при замыкании цепи
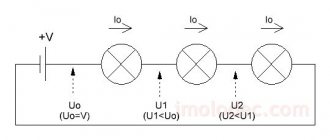
В первом опыте к батарейке подключены параллельно две лампочки, причём вторая — последовательно с катушкой достаточно большой индуктивности (рис. 3).
Ключ вначале разомкнут.
При замыкании ключа лампочка 1 загорается сразу, а лампочка 2 — постепенно. Дело в том, что в катушке возникает ЭДС индукции, препятствующая возрастанию тока. Поэтому максимальное значение тока во второй лампочке устанавливается лишь спустя некоторое заметное время после вспыхивания первой лампочки.
Это время запаздывания тем больше, чем больше индуктивность катушки. Объяснение простое: ведь тогда больше будет напряжённость вихревого электрического поля, возникающего в катушке, и потому батарейке придётся совершить большую работу по преодолению вихревого поля, тормозящего заряженные частицы.
Во втором опыте к батарейке подключены параллельно катушка и лампочка (рис. 4). Сопротивление катушки много меньше сопротивления лампочки.
Рис. 4. Самоиндукция при размыкании цепи
Ключ вначале замкнут. Лампочка не горит — напряжение на ней близко к нулю из-за малости сопротивления катушки. Почти весь ток, идущий в неразветвлённой цепи, проходит через катушку.
При размыкании ключа лампочка ярко вспыхивает! Почему? Ток через катушку начинает резко убывать, и возникает значительная ЭДС индукции, поддерживающая убывающий ток (ведь ЭДС индукции, как видно из (2), пропорциональна скорости изменения тока).
Иными словами, при размыкании ключа в катушке появляется весьма большое вихревое электрическое поле, разгоняющее свободные заряды. Под действием этого вихревого поля через лампочку пробегает импульс тока, и мы видим яркую вспышку. При достаточно большой индуктивности катушки ЭДС индукции может стать существенно больше ЭДС батарейки, и лампочка вовсе перегорит.
Лампочку-то, может, и не жалко, но в промышленности и энергетике данный эффект является серьёзной проблемой. Так как при размыкании цепи ток начинает уменьшаться очень быстро, возникающая в цепи ЭДС индукции может значительно превышать номинальные напряжения и достигать опасно больших величин. Поэтому в агрегатах, потребляющих большой ток, предусмотрены специальные аппаратные меры предосторожности (например, масляные выключатели на электростанциях), препятствующие моментальному размыканию цепи.
Электромеханическая аналогия
Нетрудно заметить определённую аналогию между индуктивностью в электродинамике и массой в механике.
1. Чтобы разогнать тело до заданной скорости, требуется некоторое время — мгновенно изменить скорость тела не получается. При неизменной силе, приложенной к телу, это время тем больше, чем больше масса тела.
Чтобы ток в катушке достиг своего максимального значения, требуется некоторое время; мгновенно ток не устанавливается. Время установления тока тем больше, чем больше индуктивность катушки.
2. Если тело налетает на неподвижную стену, то скорость тела уменьшается очень быстро. Стена принимает на себя удар, и его разрушительное действие тем сильнее, чем больше масса тела.
При размыкании цепи с катушкой ток уменьшается очень быстро. Цепь принимает на себя «удар» в виде вихревого электрического поля, порождаемого убывающим магнитным полем тока, и этот «удар» тем сильнее, чем больше индуктивность катушки. ЭДС индукции может достичь столь больших величин, что пробой воздушного промежутка выведет из строя оборудование.
На самом деле эти электромеханические аналогии
простираются довольно далеко;они касаются не только индуктивности и массы, но и других величин, и оказываются весьма полезными на практике. Мы ещё поговорим об этом в листке про электромагнитные колебания.
Что такое самоиндукция – для чайников
Любой электронный проводник имеет переменное магнитное поле, которое порождает дополнительный, так называемый индукционный ток. И если рассматривать в качестве проводника – электрическую цепь, то при изменении силы тока в ней изменится и магнитное поле, которое спровоцирует возникновение вихревого электрического поля.
Подобные явления станут причиной появления электродвижущей силы (ЭДС) в той же самой цепи, что и является самоиндукцией. Таким образом, самоиндукцией считается явление, во время которого в электрическом проводнике возникает ЭДС из-за изменения тока в самом проводнике. Именно самоиндукция мешает току приобрести определенное значение при резком замыкании или размыкании электрической цепи, так как ЭДС в проводнике во время нарастания тока направлена в противоположную сторону относительно источника питания и наоборот во время его уменьшения.
Явление самоиндукции можно наглядно увидеть при включении или выключении 2 одинаковых ламп, которые соединены параллельно.
При этом ЭДС самоиндукции можно рассчитать по формуле:
Ɛ=-dФ/dt, где:
- Ɛ – непосредственно ЭДС;
- dФ – изменения магнитного поля;
- dt – промежуток времени, за который произошли изменения.
ЭДС измеряется в вольтах, когда единицей измерения магнитного поля является вебер.
Самоиндукция
Представим себе любую электрическую цепь, параметры которой можно менять. Если мы изменим силу тока в этой цепи — например, подкрутим реостат или подключим другой источник тока — произойдет изменение магнитного поля. В результате этого изменения в цепи возникнет дополнительный индукционный ток за счет электромагнитной индукции, о которой мы говорили выше. Такое явление называется самоиндукцией, а возникающий при этом ток — током самоиндукции.
| Формула магнитного потока для самоиндукции Ф = LI Ф — собственный магнитный поток [Вб] L — индуктивность контура [Гн] I — сила тока в контуре [А] |
Онлайн-подготовка к ОГЭ по физике поможет снять стресс перед экзаменом и получить высокий балл.
Самоиндукция — это возникновение в проводящем контуре ЭДС, создаваемой вследствие изменения силы тока в самом контуре.
Самоиндукция чем-то напоминает инерцию: как в механике нельзя мгновенно остановить движущееся тело, так и ток не может мгновенно приобрести определенное значение за счет самоиндукции.
Представим цепь, состоящую из двух одинаковых ламп, параллельно подключенных к источнику тока. Если мы последовательно со второй лампой включим в эту цепь катушку, то при замыкании цепи произойдет следующее:
- первая лампа загорится практически сразу,
- вторая лампа загорится с заметным запаздыванием.
При размыкании цепи сила тока быстро уменьшается, и возникающая ЭДС самоиндукции препятствует уменьшению магнитного потока. При этом индуцированный ток направлен так же, как и исходный. ЭДС самоиндукции может во многом раз превысить внешнюю ЭДС. Поэтому электрические лампочки так часто перегорают при отключении света.
| ЭДС самоиндукции ξis — ЭДС самоиндукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] ΔI/Δt — скорость изменения силы тока в контуре [А/с] L — индуктивность [Гн] |
Знак минуса в формуле закона электромагнитной индукции указывает на то, что ЭДС индукции препятствует изменению магнитного потока, который вызывает ЭДС. При решении расчетных задач знак минуса не учитывается.
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.
Ɛ=- L(dI/dt), где:
- Ɛ – ЭДС самоиндукции;
- L-индуктивность;
- I – сила тока;
- t – время.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Трансформатор и взаимоиндукция
Если расположить две катушки в непосредственной близости, например, на одном сердечнике, то будет наблюдаться явление взаимоиндукции. Пропустим переменный ток по первой, тогда её переменный поток будет пронизывать витки второй и на её выводах появится ЭДС.
Это ЭДС будет зависеть от длины провода, соответственно количества витков, а также от величины магнитной проницаемости среды. Если их расположить просто около друг друга — ЭДС будет низким, а если взять сердечник из магнитомягкой стали – ЭДС будет значительно больше. Собственно, так и устроен трансформатор.
Интересно: такое взаимное влияние катушек друг на друга называют индуктивной связью.
Польза и вред
Такое явление, как самоиндукция, большинство людей наблюдают ежедневно, даже не осознавая этого. Так, например, принцип работы люминесцентных трубчатых ламп основан именно на явлении самоиндукции. Также данное явление можно наблюдать в цепи зажигания транспортных средств, работающих на бензине. Это возможно благодаря наличию катушки индуктивности и прерывателя. Так, в момент, когда через катушку проходит ток, прерыватель разрывает цепь питания катушки, в результате чего и образуется ЭДС, которая далее приводит к тому, что импульс более 10 кВ поступает на свечи зажигания.
Явление самоиндукции также приносит пользу, убирая лишнюю пульсацию, частоты или различные шумы в музыкальных колонках или другой аудиотехнике. Именно на ней основано работа различных «шумовых» фильтров.
Однако самоиндукция способна приносить не только пользу, но и заметный вред. Особенно часто она вредит различным выключателям, рубильникам, розеткам и другим устройствам, размыкающим электрическую цепь. Ее негативное воздействие на электроприборы можно заметить невооруженным глазом: искра в розетке в момент вытаскивания вилки, работающего фена и есть проявление сопротивления изменению силы тока.
Будет интересно➡ Что такое УЗО?
Именно поэтому лампочки чаще всего перегорают именно в момент выключения света, а не наоборот. Это связано с тем, что сопротивление приводит к выгоранию контактов и накоплению цепей с токами в различных электроприборах, что в свою очередь представляет собой довольно серьезную техническую проблему.
Индуктивность и самоиндукция – незнакомые многим термины, с которыми люди встречаются ежедневно. И если первый термин является физической величиной, обозначающей способность проводника препятствовать изменению напряжения, то второй объясняет появление ЭДС индукции в том же проводнике.
Формулы
Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.
При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:
где Eсамоинд. – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.
Энергия магнитного поля
Энергия магнитного поля контура индуктивности L
с силой тока
I
\(~W_m = \dfrac{L \cdot I^2}{2}.\)
Так как \(~\Phi = L \cdot I\), то энергию магнитного поля тока (катушки) можно рассчитать, зная любые две величины из трех (Φ, L, I
):
\(~W_m = \dfrac{L \cdot I^2}{2} = \dfrac{\Phi \cdot I}{2}=\dfrac{\Phi^2}{2L}.\)
Энергию магнитного поля, заключенную в единице объема пространства, занятого полем, называют объемной плотностью энергии
магнитного поля:
\(\omega_m = \dfrac{W_m}{V}.\)
*Вывод формулы
1 вывод.
Подключим к источнику тока проводящий контур с индуктивностью L
. Пусть за малый промежуток времени Δt сила тока равномерно увеличится от нуля до некоторого значения
I
(Δ
I
=
I
). ЭДС самоиндукции будет равна
\(E_{si} =-L \cdot \dfrac{\Delta I}{\Delta t} = -L \cdot \dfrac{I}{\Delta t}.\)
За данный промежуток время Δt
через контур переносится заряд
\(\Delta q = \left\langle I \right \rangle \cdot \Delta t,\)
где \(\left \langle I \right \rangle = \dfrac{I}{2}\) — среднее значение силы тока за время Δt
при равномерном его возрастании от нуля до
I
.
Сила тока в контуре с индуктивностью L
достигает своего значения не мгновенно, а в течение некоторого конечного промежутка времени Δ
t
. При этом в цепи возникает ЭДС самоиндукции Esi, препятствующая нарастанию силы тока. Следовательно, источник тока при замыкании совершает работу против ЭДС самоиндукции, т.е.
\(A = -E_{si} \cdot \Delta q.\)
Работа, затраченная источником на создание тока в контуре (без учета тепловых потерь), и определяет энергию магнитного поля, запасаемую контуром с током. Поэтому
\(W_m = A = L \cdot \dfrac{I}{\Delta t} \cdot \dfrac{I}{2} \cdot \Delta t = \dfrac{L \cdot I^2}{2}.\)
2 вывод
.
Если магнитное поле создано током, проходящим в соленоиде, то индуктивность и модуль индукции магнитного поля катушки равны
\(~L = \mu \cdot \mu_0 \cdot \dfrac {N^2}{l} \cdot S, \,\,\, ~B = \dfrac {\mu \cdot \mu_0 \cdot N \cdot I}{l}\)
или
\(I = \dfrac {B \cdot l}{\mu \cdot \mu_0 \cdot N}.\)
Подставив полученные выражения в формулу для энергии магнитного поля, получим
\(~W_m = \dfrac {1}{2} \cdot \mu \cdot \mu_0 \cdot \dfrac {N^2}{l} \cdot S \cdot \dfrac {B^2 \cdot l^2}{(\mu \cdot \mu_0)^2 \cdot N^2} = \dfrac {1}{2} \cdot \dfrac {B^2}{\mu \cdot \mu_0} \cdot S \cdot l.\)
Так как \(~S \cdot l = V\) — объем катушки, плотность энергии магнитного поля равна
\(\omega_m = \dfrac {B^2}{2\mu \cdot \mu_0},\)
где В
— модуль индукции магнитного поля, μ — магнитная проницаемость среды, μ0 — магнитная постоянная.
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Индуктивность контура. Самоиндукция
Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное поле, индукция которого, по закону Био — Савара—Лапласа (см. (110.2)), пропорциональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорционален току I
в контуре:
Ф=LI,
(126.1)
где коэффициент пропорциональности L
называется
индуктивностью контура.
При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в проводящем контуре при изменении в нем силы тока называется самоиндукцией.
Из выражения (126.1) определяется единица индуктивности генри
(Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:
1 Гн=1 Вб/А=1В•с/А.
Рассчитаем индуктивность бесконечно длинного соленоида. Согласно (120.4), полный магнитный поток через соленоид
(потокосцепление) равен m0m(N2I/l
)
S.
Подставив это выражение в формулу (126.1), получим
т. е. индуктивность соленоида зависит от числа витков соленоида N,
его длины
l
, площади S и магнитной проницаемости m вещества, из которого изготовлен сердечник соленоида.
Можно показать, что индуктивность контура в общем случае зависит только от геометрической формы контура, его размеров и магнитной проницаемости той среды, в которой он находится. В этом смысле индуктивность контура — аналог электрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды (см. §93).
Применяя к явлению самоиндукции закон Фарадея (см. (123.2)), получим, что э.д.с. самоиндукции
Если контур не деформируется и магнитная проницаемость среды не изменяется (в дальнейшем будет показано, что последнее условие выполняется не всегда), то L
=const и
где знак минус, обусловленный правилом Ленца, показывает, что наличие индуктивности в контуре приводит к замедлению изменения
тока в нем.
Если ток со временем возрастает, то
dI/dt>0 и ξs<0, т. е. ток самоиндукции
направлен навстречу току, обусловленному внешним источником, и тормозит его возрастание. Если ток со временем убывает, то dI/dt<0 и ξs>
0
,
т. е. индукционный
ток имеет такое же направление, как и убывающий ток в контуре, и замедляет его убывание. Таким образом, контур, обладая определенной индуктивностью, приобретает электрическую инертность, заключающуюся в том, что любое изменение тока тормозится тем сильнее, чем больше индуктивность контура.
$ 127. Токи при размыкании и замыкании цепи
При всяком изменении силы тока в проводящем контуре возникает э.д.с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции.
Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.
Рассмотрим процесс выключения тока в цепи, содержащей источник тока с э.д.с. ξ, резистор сопротивлением R
и катушку индуктивностью
L.
Под действием внешней э.д.с. в цепи течет постоянный ток
I
0=ξ/
R
(внутренним сопротивлением источника тока пренебрегаем).
В момент времени t=
0отключим источник тока. Ток через катушку индуктивности
L
начнет уменьшаться, что приведет к возникновению э.д.с. самоиндукции ξ
s=-LdI/dt,
препятствующей, согласно правилу Ленца, уменьшению тока. В каждый момент времени ток в цепи определяется законом Ома
I=ξs/R,
или
IR=-LdI/dt.
(127.1)
Разделив в выражении (127.1) переменные, получим dI/I
=
-(R/L)dt.
Интегрируя
это уравнение по I
(от I0 до I) и
t
(от 0 до t), находим ln(I/I0)=-
Rt/L,
или
где t=L/R — постоянная, называемая временем релаксации.
Из (127.2) следует, что т есть время, в течение которого сила тока уменьшается в е раз.
Таким образом, в процессе отключения источника э.д.с. сила тока убывает по экспоненциальному закону (127.2) и определяется кривой 1
на рис. 183. Чем больше индуктивность цепи и меньше ее сопротивление, тем больше т и, следовательно, тем медленнее уменьшается ток в цепи при ее размыкании.
При замыкании цепи помимо внешней э.д.с.ξ возникает э.д.с. самоиндукции
ξs=-LdI/dt,
препятствующая, согласно
правилу Ленца, возрастанию тока. По закону Ома, IR=ξ+ξs, или
IR
=
ξ-LdI/dt
.
Введя новую переменную u=IR-ξ,
преобразуем это уравнение к виду
du/u=-dt/t,
где 1 —
время релаксации.
В момент замыкания (t=0) сила тока I
=0 и
u=-ξ.
Следовательно, интегрируя по и (от -ξ до
IR — ξ)
и t (от 0 до t).
находим ln(IR
-ξ)/-ξ
=-t/t,
или
где I
0=ξ
/R
— установившийся ток (при t®¥)
Таким образом, в процессе включения источника э.д.с. нарастание силы тока в цепи задается функцией (127.3) и определяется кривой 2
на рис. 183. Сила тока возрастает от начального значения
I
=0 и асимптотически стремится к установившемуся значению
I
0
=ξ/R.
Скорость нарастания тока определяется тем же временем релаксации t
=L/R,
что и убывание тока. Установление тока происходит тем быстрее, чем меньше индуктивность цепи и больше ее сопротивление.
Оценим значение э.д.с. самоиндукции ξs,
возникающей при мгновенном увеличении сопротивления цепи постоянного тока от
R
0 До
R.
Предположим, что мы размыкаем контур, когда в нем течет установившийся ток
I
0=ξ/R0. При размыкании цепи ток изменяется по формуле (127.2). Подставив в нее выражение для
I
0 и t, получим
Э.д.с. самоиндукции
т. е. при значительном увеличении сопротивления цепи (R/R
0
>>
1
)
обладающей большой индуктивностью, э.д.с. самоиндукции может во много раз превышать э.д.с. источника тока, включенного в цепь. Таким образом, необходимо учитывать, что контур, содержащий индуктивность, нельзя резко размыкать, так как это (возникновение значительных э.д.с. самоиндукции) может привести к пробою изоляции и выводу из строя измерительных приборов. Если в контур сопротивление вводить постепенно, то э.д.с. самоиндукции не достигнет больших значений.
Взаимная индукция
Рассмотрим два неподвижных контура (1 к 2),
расположенных достаточно близко друг от друга (рис. 184). Если в контуре
1
течет ток
I
1
,
то магнитный поток, создаваемый этим током (поле, создающее этот поток, на рисунке изображено сплошными линиями), пропорционален
I
1. Обоз
начим через Ф21 ту часть потока, которая пронизывает контур
2.
Тогда
Ф21=L
21/
I
1, (128.1)
где L
21 — коэффициент пропорциональности.
Если ток I
1 изменяется, то в контуре
2
индуцируется э.д.с. ξi2
,
которая по закону Фарадея (см. (123.2)) равна и противоположна по знаку скорости изменения магнитного потока Ф21, созданного током в первом контуре и пронизывающего второй:
Аналогично, при протекании в контуре 2
тока I2 магнитный поток (его поле изображено на рис. 184 штриховой линией) пронизывает первый контур. Если Ф12— часть этого потока, пронизывающего контур
1
, то
Ф12 =L
12
I
2.
Если ток I
2 изменяется, то в контуре
1
индуцируется э.д.с. ξi1
,
которая равна и противоположна по знаку скорости изменения магнитного потока Ф12, созданного током во втором контуре и пронизывающего первый:
Явление возникновения э.д.с. в одном из контуров при изменении силы тока в другом называется взаимной индукцией.
Коэффициенты пропорциональности
L
21 и
L
12 называются
взаимной индуктивностью контуров.
Расчеты, подтверждаемые опытом, показывают, что
l
21и
L
12равны друг другу, т. е.
L
I2 =
L
2I. (128.2)
Коэффициенты L
12и
L
21 зависят от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры среды. Единица взаимной индуктивности та же, что и для индуктивности,— генри (Гн).
Рассчитаем взаимную индуктивность двух катушек, намотанных на общий тороидальный сердечник. Этот случай имеет большое практическое значение (рис. 185). Магнитная индукция поля, создаваемого первой катушкой с числом витков N
1, током
I
1 и магнитной проницаемостью m, сердечника, согласно (119.2),
B=m
0
mN
1
I
1
/l,
где
l
— длина сердечника
по средней линии. Магнитный поток через один виток второй катушки Ф2=BS=m0m(N
1
I
1/
l
)S Тогда полный магнитный поток (потокосцепление) сквозь вторичную обмотку, содержащую
N2
витков,
Поток yсоздается током I
1
,
поэтому, согласно (128.1), получаем
Если вычислить магнитный поток, создаваемый катушкой 2
сквозь катушку
1
, то для
L
12 получим выражение в соответствии с формулой (128.3). Таким образом, взаимная индуктивность двух катушек, намотанных на общий тороидальный сердечник,
Трансформаторы
Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении взаимной индукции. Впервые трансформаторы были сконструированы и введены в практику русским электротехником П. Н. Яблочковым (1847—1894) и русским физиком И. Ф. Усагиным (1855—1919). Принципиальная схема трансформатора показана на рис. 186.
Первичная и вторичная катушки (обмотки), имеющие соответственно n
1и
N
2 витков, укреплены на замкнутом железном сердечнике. Так как концы первичной обмотки присоединены к источнику переменного напряжения с э.д.с. ξ1
,
то в ней возникает переменный ток
I
1
,
создающий в сердечнике трансформатора переменный магнитный поток Ф, который практически полностью локализован в железном сердечнике и, следовательно, почти целиком пронизывает витки вторичной обмотки. Изменение этого потока вызывает во вторичной обмотке появление э.д.с. взаимной индукции, а в первичной — э.д.с. самоиндукции.
Ток I
1 первичной обмотки определяется согласно закону Ома:
где R
1— сопротивление первичной обмотки. Падение напряжения
I
1
R
1на сопротивлении
R
1 при быстропеременных полях мало по сравнению с каждой из двух э.д.с., поэтому
Э.д.с. взаимной индукции, возникающая во вторичной обмотке,
Сравнивая выражения (129.1) и (129.2), получим, что э.д.с.
, возникающая во вторичной обмотке,
где знак минус показывает, что э.д.с. в первичной и вторичной обмотках противоположны по фазе.
Отношение числа витков N
2
/N
1
,
показывающее, во сколько раз э.д.с. во вторичной обмотке трансформатора больше (или меньше), чем в первичной, называется
коэффициентом трансформации.
Пренебрегая потерями энергии, которые в современных трансформаторах не превышают 2 % и связаны в основном с выделением в обмотках джоулевой теплоты и появлением вихревых токов, и применяя закон сохранения энергии, можем записать, что мощности тока в обеих обмотках трансформатора практически одинаковы:
ξ
2
I
2
»ξ
1
I
1
,
откуда, учитывая соотношение (129.3), найдем
ξ2/ξ1=I
1/
I
2 =
N
2/
N
1,
т. е. токи в обмотках обратно пропорциональны числу витков в этих обмотках.
Если N
2
/N
1>1, то имеем дело с
повышающим трансформатором,
увеличивающим переменную э.д.с. и понижающим ток (применяются, например, для передачи электроэнергии на большие расстояния, так как в данном случае потери на джоулеву теплоту, пропорциональные квадрату силы тока, снижаются); если
N2/N
1<1
,
то имеем дело с
понижающим трансформатором,
уменьшающим э.д.с. и повышающим ток (применяются, например, при электросварке, так как для нее требуется большой ток при низком напряжении).
Мы рассматривали трансформаторы, имеющие только две обмотки. Однако
трансформаторы, используемые в радиоустройствах, имеют 4—5 обмоток, обладающих разными рабочими напряжениями. Трансформатор, состоящий из одной обмотки, называется автотрансформатором.
В случае повышающего автотрансформатора э.д.с. подводится к части обмотки, а вторичная э.д.с. снимается со всей обмотки. В понижающем автотрансформаторе напряжение сети подается на всю обмотку, а вторичная э.д.с. снимается с части обмотки.
Энергия магнитного поля
Проводник, по которому протекает электрический ток, всегда окружен магнитным полем, причем магнитное поле появляется и исчезает вместе с появлением и исчезновением тока. Магнитное поле, подобно электрическому, является носителем энергии. Естественно предположить, что энергия магнитного поля равна работе, которая затрачивается током на создание этого поля.
Рассмотрим контур индуктивностью L,
по которому течет ток
I
. С данным контуром сцеплен магнитный поток (см. (126.1)) Ф=
LI
, причем при изменении тока на d
I
магнитный поток изменяется на dФ=
L
d
I
. Однако для изменения магнитного потока на величину dФ (см. § 121) необходимо совершить работу d
A
=
I
dФ=
LI
d
I.
Тогда работа по созданию магнитного потока Ф будет равна
Следовательно, энергия магнитного поля, связанного с контуром,
W=LI2/2.
(130.1)
Исследование свойств переменных магнитных полей, в частности распространения электромагнитных волн, явилось доказательством того, что энергия магнитного поля локализована в пространстве. Это соответствует представлениям теории поля.
Энергию магнитного поля можно представить как функцию величин, характеризующих это поле в окружающем пространстве. Для этого рассмотрим частный случай — однородное магнитное поле внутри длинного соленоида. Подставив в формулу (130.1) выражение (126.2), получим
Так как I=Вl/
(m0mN) (см. (119.2)) и
В=m
0
mH
(см. (109.3)), то
где Sl
=
V —
объем соленоида.
Магнитное поле соленоида однородно и сосредоточено внутри него, поэтому энергия (см. (130.2)) заключена в объеме соленоида и распределена в нем с постоянной объемной плотностью
Выражение (130.3) для объемной плотности энергии магнитного поля имеет вид, аналогичный формуле (95.8) для объемной плотности энергии электростатического поля, с той разницей, что электрические величины заменены в нем магнитными. Формула (130.3) выведена для однородного поля, но она справедлива и для неоднородных полей. Выражение (130.3) справедливо только для сред, для которых зависимость В
от
Н линейная,
т. е. оно относится только к пара- и диамагнетикам
Вихревое электрическое поле
Из закона Фарадея ξ=dФ/dt
следует, что
любое
изменение
сцепленного с контуром потока магнитной индукции приводит к возникновению электродвижущей силы индукции и вследствие этого появляется индукционный ток. Следовательно, возникновение э.д.с. электромагнитной индукции возможно и в неподвижном контуре, находящемся в переменном магнитном поле. Однако э.д.с. в любой цепи возникает только тогда, когда в ней на носители тока действуют сторонние силы — силы неэлектростатического происхождения. Поэтому возникает вопрос о природе сторонних сил в данном случае.
Опыт показывает, что эти сторонние силы не связаны ни с тепловыми, ни с химическими процессами в контуре; их возникновение также нельзя объяснить силами Лоренца, так как они на неподвижные заряды не действуют. Максвелл высказал гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое
и является причиной возникновения индукционного тока в контуре. Согласно представлениям Максвелла, контур, в котором появляется э.д.с., играет второстепенную роль, являясь своего рода лишь «прибором», обнаруживающим это поле.
Итак, по Максвеллу, изменяющееся во времени магнитное поле порождает электрическое поле ЕB
, циркуляция которого, по (123.3),
где EBl
— проекция вектора
E
B на направление d
l
.
Подставив в формулу (137.1) выражение , получим
Если поверхность и контур неподвижны, то операции дифференцирования и интегрирования можно поменять местами. Следовательно,
где символ частной производной подчеркивает тот факт, что интеграл является
функцией только от времени.
Согласно (83.3), циркуляция вектора напряженности электростатического поля (обозначим его e
q) вдоль любого замкнутого контура равна нулю:
Сравнивая выражения (137.1) и (137.3), видим, что между рассматриваемыми полями (Е
B и
e
q) имеется принципиальное различие: циркуляция вектора
Е
B в отличие от циркуляции вектора
e
q не равна нулю. Следовательно, электрическое поле
Е
B, возбуждаемое магнитным полем, как и само магнитное поле, является
вихревым.
Ток смещения
Согласно Максвеллу, если всякое переменное магнитное поле возбуждает в окружающем пространстве вихревое электрическое поле, то должно существовать и обратное явление: всякое изменение электрического поля должно вызывать появление в окружающем пространстве вихревого магнитного поля. Для установления количественных соотношений между изменяющимся электрическим полем и вызываемым им магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения.
Рассмотрим цепь переменного тока, содержащую конденсатор (рис. 196). Между обкладками заряжающегося и разряжающегося конденсатора имеется переменное электрическое поле, поэтому, согласно Максвеллу, через конденсатор
«протекают» токи смещения, причем в тех участках, где отсутствуют проводники.
Найдем количественную связь между изменяющимся электрическим и вызываемым им магнитным полями. По Максвеллу, переменное электрическое поле в конденсаторе в каждый момент времени создает такое магнитное поле, как если бы между обкладками конденсатора существовал ток проводимости, равный току в подводящих проводах. Тогда можно утверждать, что токи проводимости (I
) и смещения (
I
см) равны:
I
см=
I
. Ток проводимости вблизи обкладок конденсатора
(поверхностная плотность заряда sна обкладках равна электрическому смещению D
в конденсаторе (см. (92.1)). Подынтегральное выражение в (138.1) можно рассматривать как частный случай скалярного произведения (
дD
/
д
t)d
S
, когда
дD
/
д
t и d
S
взаимно параллельны. Поэтому для общего случая можно записать
Сравнивая это выражение с I
=
I
см = (см. (96.2)), имеем
Выражение (138.2) и было названо Максвеллом плотностью тока смещения.
Рассмотрим, каково же направление векторов плотностей токов проводимости и смещения j
и
j
см. При зарядке конденсатора (рис. 197, а) через проводник, соединяющий обкладки, ток течет от правой обкладки к левой; поле в конденсаторе усиливается, вектор D растет со временем;
следовательно, дD
/
д
t>0, т.е. вектор
дD
/
д
t
направлен в ту же сторону, что и D. Из рисунка видно, что направления векторов
дD
/
д
t и
j
совпадают. При разрядке конденсатора (рис. 197, б) через проводник, соединяющий обкладки, ток течет от левой обкладки к правой; поле в конденсаторе ослабляется, вектор
D
убывает со временем; следовательно,
дD
/
д
t<0, т. е. вектор
at
дD
/
д
t направлен противоположно вектору
D. Однако вектор дD
/
д
t направлен опять так
же, как и вектор j
. Из разобранных примеров следует, что направление вектора
j
, а следовательно, и вектора
j
см совпадает
с
направлением вектора
дD
/
д
t,
как это и следует из формулы (138.2).
Подчеркнем, что из всех физических свойств, присущих току проводимости, Максвелл приписал току смещения лишь одно — способность создавать в окружающем пространстве магнитное поле. Таким образом, ток смещения (в вакууме или веществе) создает в окружающем пространстве магнитное поле (линии индукции магнитных полей токов смещения при зарядке и разрядке конденсатора показаны на рис. 197 штриховой линией).
В диэлектриках ток смещения состоит из двух слагаемых. Так как, согласно (89.2), D
=e0
E
+
P
, где
Е
— напряженность электростатического поля, а
Р
— поляризованность (см. § 88), то плотность тока смещения
где e0дE
/
д
t
— плотность тока смещения
в вакууме,дP
/
д
t
— плотность тока поляризации
— тока, обусловленного упорядоченным движением электрических зарядов в диэлектрике (смещение зарядов в неполярных молекулах или поворот диполей в полярных молекулах). Возбуждение магнитного поля токами поляризации правомерно, так как токи поляризации по своей природе не отличаются от токов проводимости. Однако то, что и другая
(e0дE
/
д
t),
часть плотности тока смещения (e0дE
/
д
t),
не связанная с движением зарядов, а обусловленная только
изменением электрического поля во времени, также возбуждает магнитное поле, является
принципиально новым утверждением
Максвелла. Даже в вакууме всякое изменение во времени электрического поля приводит к возникновению в окружающем пространстве магнитного поля.
Следует отметить, что название «ток смещения» является условным, а точнее — исторически сложившимся, так как ток смещения по своей сути — это изменяющееся со временем электрическое поле. Ток смещения поэтому существует не только в вакууме или диэлектриках, но и внутри проводников, по которым течет переменный ток. Однако в данном случае он пренебрежимо мал по сравнению с током проводимости. Наличие токов смещения подтверждено экспериментально советским физиком А. А. Эйхенвальдом, изучавшим магнитное поле тока поляризации, который, как следует из (138.3), является частью тока смещения.
Максвелл ввел понятие полного тока,
равного сумме токов проводимости (а также конвекционных токов) и смещения.
Плотность полного тока
jполн=j+дD
/
д
t.
Введя понятия тока смещения и полного тока, Максвелл по-новому подошел к рассмотрению замкнутости цепей переменного тока. Полный ток в них всегда замкнут, т. е. на концах проводника обрывается лишь ток проводимости, а в диэлектрике (вакууме) между концами проводника имеется ток смещения, который замыкает ток проводимости.
Максвелл обобщил теорему о циркуляции вектора Н
(см. (133.10)), введя в ее правую часть полный ток
I
полн= сквозь поверхность
S,
натянутую на замкнутый контур
L.
Тогда
обобщенная теорема о циркуляции вектора Н
запишется в виде
Выражение (138.4) справедливо всегда, свидетельством чего является полное соответствие теории и опыта.
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
| Закон Фарадея Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] |
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
| Закон Фарадея для контура из N витков Ɛi — ЭДС индукции [В] ΔФ/Δt — скорость изменения магнитного потока [Вб/с] N — количество витков [-] |
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
| Закон Ома для проводящего контура Ɛi — ЭДС индукции [В] I — сила индукционного тока [А] R — сопротивление контура [Ом] |
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
| ЭДС индукции для движущегося проводника Ɛi — ЭДС индукции [В] B — магнитная индукция [Тл] v — скорость проводника [м/с] l — длина проводника [м] |
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Магнитный поток
Прежде чем говорить об электромагнитной индукции и самоиндукции, нам нужно определить сущность магнитного потока.
Представьте, что вы взяли в руки обруч и вышли на улицу в ливень. Потоки воды будут проходить через обруч.
Если держать обруч горизонтально, то через него пройдет много воды. А если начать его поворачивать — уже меньше, потому что он расположен не под прямым углом к вертикали.
Теперь давайте поставим обруч вертикально — ни одной капли не пройдет сквозь него (если ветер не подует, конечно).
Магнитный поток очень похож на поток воды, проходящей через обруч, только считаем мы величину прошедшего через площадь магнитного поля, а не дождя.
Магнитным потоком через площадь S контура называют скалярную физическую величину, равную произведению:
- модуля вектора магнитной индукции B,
- площади поверхности S, которую пронизывает поток,
- и косинуса угла α между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности).
| Магнитный поток Ф — магнитный поток [Вб] B — магнитная индукция [Тл] S — площадь пронизываемой поверхности [м2] n — вектор нормали (перпендикуляр к поверхности) [-] |
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла α магнитный поток может быть положительным (α < 90°) или отрицательным (α > 90°). Если α = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно, меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Как спользуют силу самоиндукции в жизни:
Физика – ничто без практического применения. Явление самоиндукции активно используют в обычной жизни. Например, в работе карбюраторного двигателя участвует катушка зажигания.
Катушка зажигания получает заряд в 12 В. Электрическая цепь прекращается с помощью специального прерывателя. Из-за этого образуется сильная искра, зажигающая топливо. Автомобиль начинает движение. В современных машинах разрыв цепи происходит автоматически, но принцип самоиндукции сохраняется.
Самоиндукцию также применяют в работе сетевых фильтров. Она помогает сгладить всплески напряжения и заполнить провалы в подаче тока. В результате, удается убрать шум, пульсацию и ненужные частоты.
Самоиндукцию катушки применяют для розжига электродов в газоразрядных источниках света. Когда срабатывает стартер, контакты перерываются, из-за чего в катушке возникает ЭДС самоиндукции. Лампа начинает выполнять свою функцию за счет всплеска энергии.
Примеры использования на практике
Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.
Работает этот важный узел следующим образом:
- На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
- Электрическая цепь резко обрывается специальным прерывателем.
- Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
- Искровой разряд зажигает топливную смесь, приводя в движение поршень.
В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.
Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.
В блоках питания электронной аппаратуры таким же способом убирают:
- шумы:
- пульсации;
- нежелательные частоты.
Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.
Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.
В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.
В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.
Урок по физике «Самоиндукция. Индуктивность. Энергия магнитного поля тока» (8 класс )
План–конспект урока по физике «Самоиндукция. Индуктивность. Энергия магнитного поля тока» (8 класс )
Тема урока: Самоиндукция. Индуктивность. Энергия магнитного поля.
Цель:
Формирование понятия явления самоиндукции, его проявлении в цепях электрического тока. Применение самоиндукции в электротехнических устройствах.
Задачи:
Образовательные:
Повторить знание учащихся о явление электромагнитной индукции, углубить их; на этой основе изучить явление самоиндукции.
Воспитательные:
Воспитать интерес к предмету, трудолюбие и умение внимательно оценивать ответы товарищей. Показать значение причинно- следственных связей в познаваемости явлений.
Развивающие:
Развитие физического мышления учащихся, расширение понятийного аппарата учащихся, формирование умений анализировать информацию, делать выводы из наблюдений и опытов.
Тип урока:
урок изучения нового материала.
Оборудование:
Катушка индуктивности с сердечником – демонстрационная, источник питания, ключ, две лампочки на 3,5 В, реостат на 100 Ом, неоновая лампочка на 200В.
Опыты:
1) опыт по наблюдению явления самоиндукции при замыкании цепи; 2) опыт по наблюдению явления самоиндукции при размыкании цепи;
План урока:
- Организационный момент.
- Актуализация опорных знаний.
- Мотивация.
- Изучение нового материала.
- Закрепление.
- Домашнее задание.
Ход урока
- Организационный момент.
(1 мин)
- Актуализация опорных знаний.
— Что называют явлением электромагнитной индукции?
-Какая гипотеза Фарадея привела к открытию электромагнитной индукции?
-Как Фарадей открыл явление электромагнитной индукции?
-При каких условиях возникает индукционный ток в катушке?
— Отчего зависит направление индукционного тока?
-Чем объясняется отталкивание алюминиевого кольца при введение в него магнита и притяжение к магниту при его удалении из кольца?
— Почему разрезанное алюминиевое кольцо не взаимодействует с движущимся магнитом?
— Сформулируйте правило Ленца.
-Как с помощью правила Ленца определить направление индукционного тока в проводнике?
3 . Мотивация.
Основы электродинамики были заложены Ампером в 1820 году. Работы Ампера вдохновили многих инженеров на конструирование различных технических устройств, таких как электродвигатель (конструктор Б.С. Якоби), телеграф (С. Морзе), электромагнит, конструированием которого занимался известный американский ученый Генри. Создавая различные электромагниты, в 1832 году ученый открыл новое явление в электромагнетизме – явление самоиндукции. Об этом мы будем говорить на этом уроке.
4.Изучение нового материала
.
Рассмотрим частный случай электромагнитной индукции: возникновение индукционного тока в катушке при изменении силы тока в ней.
Для этого проведём опыт, изображённый на рисунке. Замкнём цепь ключом Кл. Лампа Л1 загорится сразу, а Л2 — с опозданием приблизительно в 1 с. Причина запаздывания заключается в следующем. Согласно явлению электромагнитной индукции, в реостате и в катушке возникают индукционные токи. Они препятствуют увеличению силы тока I1 и I2 (это следует из правила Ленца и правила правой руки). Но в катушке К индукционный ток будет значительно больше, чем в реостате Р, так как катушка имеет гораздо большее число витков и сердечник, т. е. обладает большей индуктивностью, чем реостат.
В проделанном опыте мы наблюдаем явление самоиндукции.
Явление самоиндукции заключается в возникновении индукционного тока в катушке при изменении силы тока в ней. При этом возникающий индукционный ток называется током самоиндукции.
Это явление было открыто Джозефом Генри, практически одновременно с открытием явлением электромагнитной индукции Фарадеем.
Самоиндукция при размыкании электрической цепи и энергия магнитного поля.
Появление мощного индукционного тока при размыкании цепи свидетельствует о том, что магнитное поле тока в катушке обладает энергией. Именно за счёт уменьшения энергии магнитного поля совершается работа по созданию индукционного тока. В этот момент вспыхивает лампа Лн которая, при нормальных условиях, загорается при напряжении 200В. А накопилась эта энергия раньше, при замыкании цепи, когда за счёт энергии источника тока совершалась работа по преодолению тока самоиндукции, препятствующего увеличению тока в цепи, и его магнитного поля.
Индуктивность
— это величина, равная ЭДС самоиндукции при изменении силы тока в проводнике на 1 А за 1 с. Единица индуктивности — генри (Гн). 1 Гн = 1 В • с/А. 1 генри — это индуктивность такого проводника, в котором возникает ЭДС самоиндукции 1 вольт при скорости изменения силы тока 1 А/с. L называют индуктивностью. Демонстрация различных катушек индуктивности применяемых в радиотехнике и электротехнике. Используем раздаточный материал для просмотра учащимися. (катушки индуктивности)
Люминесцентная лампа
– это газоразрядные источники света. Их световой поток формируется за счет свечения люминофоров, на которые воздействует ультрафиолетовое излучение разряда. Его видимое свечение обычно не превышает 1-2%. Люминесцентные лампы (ЛЛ) получили широкое применение в освещении помещений разного типа. Их световая отдача в разы больше, чем у привычных ламп накаливания. В качестве выключателя используют устройство – стартёр. Стартер представляет собой небольшую газоразрядную лампу тлеющего разряда. Стеклянная колба наполняется инертным газом (неон или смесь гелий-водород) и помещается в металлический или пластмассовый корпус. При включении схемы на напряжение сети оно полностью окажется приложенным к стартеру. Электроды стартера разомкнуты, и в нем возникает тлеющий разряд. В цепи будет проходить небольшой ток (20-50 мА). Этот ток нагревает биметаллические электроды, и они, изгибаясь, замкнут цепь, и тлеющий разряд в стартере прекратится. После зажигания лампы в цепи установится ток, равный номинальному рабочему току лампы. Этот ток обусловит такое падение напряжения на дросселе, что напряжение на лампе станет примерно равным половине номинального напряжения сети. Так как стартер включен параллельно лампе, то напряжение на нем будет равно напряжению на лампе и в связи с тем, что оно недостаточно для зажигания тлеющего разряда в стартере, его электроды останутся разомкнутыми при горении лампы.
5. Закрепление .
1. Какое явление изучалось на проделанном опыте . 2. В чём заключается явление самоиндукции? 3. Может ли возникнуть ток самоиндукции в прямом проводнике с током? Если нет, то объясните почему; если да, то при каком условии. 4. За счёт уменьшения какой энергии совершалась работа по созданию индукционного тока при размыкании цепи?
5. Какие факты доказывают, что магнитное поле обладает энергией?
6. Что такое индуктивность?
7. Назовите единицу индуктивности в СИ и как она называется?
8. Что такое дроссель и для чего он нужен при работе люминесцентной лампы?
Задача1.
Какова индуктивность катушки, если при постепенном изменении в ней силы тока от 5 до 10А за 0,1 с возникает ЭДС самоиндукции, равная 20В?
| Дано: I1=5 А I2=10 А t=0.1 c ε=20 В | L= | [L]== Гн {L}=== 0.4 Ответ : 0,4Гн |
| L — ? |
Задача2.
Найти индуктивность проводника, в котором при равномерном изменении силы тока на 2 А в течение 0,25 с возбуждается ЭДС самоиндукции 20 мВ.
6. Домашнее задание.
Читать §23 Вопросы §23 , стр 101. По желанию подготовить сообщения по темам: «Применение катушек индуктивности в электротехнике», «Применение люминесцентных ламп», «Борьба с самоиндукцией в электротехнике».
Что важно помнить об индуктивности
Как уже было отмечено, индуктивность контура может менять в зависимости от его геометрии, охвата, магнитных характеристик среды. Данные правила работают и для дросселя. Ее индуктивность может меняться в зависимости диаметра и интенсивности обмотки. Значение индуктивности также вырастет при использовании ферромагнитного сердечника.
Степень индуктивности будет меняться в соответствии с тем, как сильно передатчик, роль которого выполняют спирали, сопротивляется электрическому импульсу. При высокой индуктивности и быстрой остановке ее цепи, произойдет сильный всплеск ЭДС.
Индуктивность выражают с помощью единицы измерения «генри». 1Гн соответствует ЭДС 1В при скорости изменения тока 1А в секунду.
Значение индуктивности помогает определить, сколько энергии выделяется благодаря магнитному полю при самоиндукции. Высчитать энергию можно, применив формулировку Wм = LI2 / 2.
Самоиндукция и инерция
Явление самоиндукции проще понять, проведя аналогию с инерцией в механике. Инерция приводит к тому, что под действием силы тело не мгновенно приобретает скорость, а постепенно. Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила. Точно так же за счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы не прекращаем ток сразу. Самоиндукция его поддерживает некоторое время, несмотря на сопротивление цепи.
Чтобы увеличить скорость тела, согласно законам механики нужно совершить работу. При торможении тело само совершает работу. Точно так же для создания тока нужно совершить работу против вихревого электрического поля, а при исчезновении тока это поле совершает положительную работу.
Что такое катушка индуктивности
Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух — это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Литература
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 351-355, 432-434.
- Жилко В.В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. Обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В.В. Жилко, Л.Г. Маркович. — Мн.: Нар. асвета, 2008. — С. 183-188.
- Мякишев, Г.Я. Физика : Электродинамика. 10-11 кл. : учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. — М.: Дрофа, 2005. — С. 417-424.
ЭДС индукции
Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.
Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.
Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.
ЭДС в быту и единицы измерения
Другие примеры встречаются в практической жизни любого рядового человека. Под эту категорию попадают такие привычные вещи, как малогабаритные батарейки, а также другие миниатюрные элементы питания. В этом случае рабочая ЭДС формируется за счет химических процессов, протекающих внутри источников постоянного напряжения. Когда оно возникает на клеммах (полюсах) батареи вследствие внутренних изменений – элемент полностью готов к работе. Со временем величина ЭДС несколько снижается, а внутреннее сопротивление заметно возрастает.
В результате если вы измеряете напряжение на не подключенной ни к чему пальчиковой батарейке вы видите нормальные для неё 1.5В (или около того), но когда к батарейке подключается нагрузка, допустим, вы установили её в какой-то прибор — он не работает. Почему? Потому что если предположить, что у вольтметра внутреннее сопротивление во много раз выше, чем внутреннее сопротивлении батарейки — то вы измеряли её ЭДС. Когда батарейка начала отдавать ток в нагрузке на её выводах стало не 1.5В, а, допустим, 1.2В — прибору недостаточно ни напряжения, ни тока для нормальной работы.
Расчет ЭДС.
Как раз вот эти 0.3 В и упали на внутреннем сопротивлении гальванического элемента. Если батарейка совсем старая и её электроды разрушены, то на клеммах батареи может не быть вообще никакой электродвижущей силы или напряжения — т.е. ноль. Совсем небольшая по величине электродвижущая сила наводится и в рамках антенны приемника, которая усиливается затем специальными каскадами, и мы получаем наш телевизионный, радио и даже Wi-Fi сигнал.
Самоиндукция и переходные процессы в электрических цепях
Индуктивность электрической плитки или лампочки накаливания очень мала, и ток в этих электроприборах, при включении и выключении, возникает или исчезает практически мгновенно. Индуктивность электродвигателя велика, и он «выходит на режим» в течение нескольких минут.
Если выключить ток в большом электромагните с большим значением индукции, допустив высокую скорость уменьшения тока, то между контактами выключателя вспыхивает искра, а в случае большого тока может загореться вольтова дуга. Это опасное явление, поэтому в цепях с большой индуктивностью ток снижают постепенно, используя реостат (элемент с переменным электрическим сопротивлением).
Безопасное отключение электроэнергии – серьезна проблема. На все выключатели действуют «ударные нагрузки», возникающие из-за ЭДС самоиндукции при отключении тока, и выключатели «искрят». Для каждого типа выключателей указывается максимальное значение тока, которое можно коммутировать. Если ток превышает допустимое значение, в выключателе может вспыхнуть электрическая дуга.
На опасных производствах, в угольных шахтах, хранилищах нефтепродуктов простое искрение выключателей недопустимо. Здесь применяются взрывобезопасные выключатели, надежно защищенные герметичным пластмассовым корпусом. Цена таких выключателей в десятки раз выше, чем обычных – это необходимая плата за безопасность.
Взаимодействие электрического и магнитного полей – причина самоиндукции
Электрическое и магнитное поля взаимосвязаны: электрический ток или меняющееся электрическое поле создает магнитное поле.
В свою очередь, меняющееся магнитное поле создает электрическое поле.
Рассмотрим процессы в проводящем контуре, когда в нем меняется электрический ток (например, его включают или выключают).
- В проводнике, помещенном в меняющееся магнитное поле, наводится ЭДС.
- Если в проводнике меняется величина электрического тока – возникает меняющееся магнитное поле.
- Меняющееся магнитное поле, созданное током в проводнике, наводит ЭДС самоиндукции в этом же проводнике.
Не во всех электрических цепях возникает эффект самоиндукции. Лампочка накаливания мгновенно вспыхивает при подаче тока, и мгновенно гаснет при его отключении, а в электромагните, на который подается и выключается постоянное напряжение, процессы растянуты во времени. У лампочки и электромагнита разная инерционность.
В механике мерой инерционности является масса: чтобы привести в движение массивный предмет, нужно прикладывать усилие в течение некоторого времени.
В электротехнике мерой инерционности является величина, названная индуктивностью. Она обозначается символом L . Единица измерения индуктивности – Генри (Гн), а также производные единицы: миллиГенри (мГн), микроГенри (мкГн) и так далее. Чем больше индуктивность цепи, тем дольше и мощнее протекают переходные процессы. Лампочка накаливания имеет очень малую индуктивность, а у электромагнита индуктивность большая.
В радиотехнике и электротехнике используются дроссели – детали, имеющие нормированные значения индуктивности.
На рисунке приведена схема опыта, демонстрирующего явление самоиндукции.
Катушка, намотанная на ферритовый сердечник, имеет значительную индуктивность. Источник питания – батарейка с номиналом полтора вольта. Пока тумблер находится во включенном состоянии, лампочка горит тускло, поскольку напряжения батарейки для нее недостаточно. После размыкания тумблера лампочка вспыхивает ярко и потом гаснет.
Почему лампочка вспыхивает после отключения напряжения питания? Через нее разряжается ЭДС самоиндукции, наведенная в катушке в момент выключения напряжения.
Но почему свет не просто продолжает гореть, а вспыхивает ярче, чем при включенном тумблере? ЭДС самоиндукции превышает номинальное напряжение батарейки. Рассмотрим, от чего зависит такой эффект.