В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.
Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.
Магнитный поток
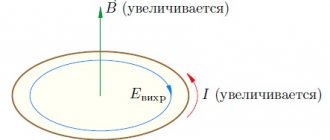
Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.
При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.
ЭДС из закона электромагнитной индукции
Магнитный поток через тот же контур, что и в примере выше, будет равняться:
Ф = B*S*cos(90-a) = B*S*sin(a).
Здесь угол (90-а) = угол между вектором магнитной индукции и нормалью к поверхности контура. За некоторое время ∆t площадь контура будет изменяться на ∆S = -l*V*∆t. Знак «минус» показывает, что площадь уменьшается. При этом за это время магнитный поток изменится:
∆Ф = -B*l*V*sin(a).
Тогда ЭДС индукции равна:
Ei = -∆Ф/∆t = B*l*V*sin(a).
Если весь контур будет двигаться внутри однородного магнитного поля с постоянной скоростью, то ЭДС индукции будет равняться нулю, так как будет отсутствовать изменение магнитного потока.
- ЭДС индукции будет возникать и при повороте рамки внутри магнитного поля.
ЭДС индукции
Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.
Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.
Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.
Пример задачи
Дано:
Контур в форме квадрата со стороной d = 0,5 м «втягивается» с постоянной скоростью v = 4 м/с в область однородного магнитного поля, величина индукции которого B = 1 Тл (см. рис. 4). Электрическое сопротивление цепи равно R = 2 Ом.
Рис. 4. Пример задачи по электростатической индукции
Нам нужно найти ответы на следующие вопросы:
a) Когда (в какой момент/моменты) в рамке будет протекать электрический ток?
б) Определите направление этого электрического тока.
(в) Вычислите значение силы, действующей на рамку при ее перемещении в соответствии с направлением вектора скорости. Предположите отсутствие механического сопротивления движению.
Решение.
(a) Индукционный ток протекает при изменении потока магнитной индукции через поверхность, охваченную контуром. В ситуации, показанной на рисунке 4, магнитный поток равен нулю и будет оставаться таковым до тех пор, пока правый край контура не коснется границы области магнитного поля. Затем, по мере движения контура, он будет все больше и больше заполняться магнитным полем — магнитный поток будет увеличиваться. Поэтому выполняется условие электромагнитной индукции, т.е. начинает протекать индукционный ток. Как долго? Это легко вычислить, поскольку движение рамы равномерно:
t = d / v = 0,5 / 2 = 0,25 секунд
Ток будет течь до тех пор, пока весь квадрат не войдет в магнитное поле. Тогда поток будет ненулевым, но больше не будет меняться.
б) Воспользуемся правилом Ленца. Мы уже заметили, что поток магнитной индукции при «втягивании» контура в магнитное поле увеличивается. Поэтому индукционный ток будет протекать в таком направлении, чтобы противодействовать увеличению потока.
Магнитное поле, создаваемое индукционным током с вектором индукции Bинд, будет противоположно вектору B.
Таким образом, вектор Bинд направлен в нашу сторону. Если расположить таким образом большой палец правой руки, остальные согнутые пальцы покажут направление индукционного тока. Ток будет течь против часовой стрелки.
(в) Снова воспользуемся равномерностью движения рамы. Обратите внимание, что сила, которая действует на рамку при ее перемещении по вектору скорости (например, сила моей руки), не может быть единственной силой, действующей на квадрат. Если бы это было так, он бы двигался с ускорением. Поскольку движение равномерное, это означает, что в каждый момент времени существует сила, которая уравновешивает силу моей руки. Это и есть электродинамическая сила. Ведь теперь в рамке течет ток, и часть его протекает в магнитном поле (см. рис. 5).
Рис. 5
Красная стрелка показывает направление электрического тока. Электродинамическая сила (сила Ампера) действует слева (я определил ее с помощью правила трех пальцев). На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
Подведем итог: электродинамическая сила уравновешивает силу моей руки. Таким образом, я могу сравнить значения обеих сил, то есть F = Fed = B * I * d, где I — сила индукционного тока. Теперь достаточно рассчитать значение силы этого тока. Мы будем использовать закон Фарадея и закон Ома для участка цепи. Давайте начнем с последнего: поскольку нас интересует только значение I, мы напишем
I = εинд / R .
| εинд | = ΔФB / Δt = Δx * d * B / Δt = ( Δx / Δt ) * d * B = v * d * B .
После подстановки в I получаем: I = εинд / R = v * d * B / R .
В конечном итоге искомое значение силы будет выражено через: Fed = B * I * d = ( B * d * v * d * B ) / R = ( B2 * d2 * v ) / R .
Подставляя численные значения получим: Fed = F = ( 12 * 0,52 * 4 ) / 2 = 0,5 Н .
Движение провода в магнитном поле
Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.
Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.
Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.
1.20. Электромагнитная индукция. Правило Ленца
Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.
Магнитным потоком Φ через площадь S контура называют величину
| Φ = B · S · cos α, |
где B – модуль вектора магнитной индукции, α – угол между вектором и нормалью к плоскости контура (рис. 1.20.1).
| Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали и выбранное положительное направление обхода контура связаны правилом правого буравчика |
Определение магнитного потока нетрудно обобщить на случай неоднородного магнитного поля и неплоского контура. Единица магнитного потока в системе СИ называется вебером (Вб). Магнитный поток, равный 1 Вб, создается магнитным полем с индукцией 1 Тл, пронизывающим по направлению нормали плоский контур площадью 1 м2:
| 1 Вб = 1 Тл · 1 м2. |
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Эта формула носит название закона Фарадея.
Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток. Это утверждение, сформулированное в 1833 г., называется правилом Ленца.
Рис. 1.20.2 иллюстрирует правило Ленца на примере неподвижного проводящего контура, который находится в однородном магнитном поле, модуль индукции которого увеличивается во времени.
| Рисунок 1.20.2. Иллюстрация правила Ленца. В этом примере а инд <� 0. Индукционный ток Iинд течет навстречу выбранному положительному направлению обхода контура |
Правило Ленца отражает тот экспериментальный факт, что инд и всегда имеют противоположные знаки (знак «минус» в формуле Фарадея). Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам.
1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Рассмотрим в качестве примера возникновение ЭДС индукции в прямоугольном контуре, помещенном в однородное магнитное поле перпендикулярное плоскости контура. Пусть одна из сторон контура длиной l скользит со скоростью по двум другим сторонам (рис. 1.20.3).
| Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон |
На свободные заряды на этом участке контура действует сила Лоренца. Одна из составляющих этой силы, связанная с переносной скоростью зарядов, направлена вдоль проводника. Эта составляющая указана на рис. 1.20.3. Она играет роль сторонней силы. Ее модуль равен
| FЛ = eυB |
Работа силы FЛ на пути l равна
| A = FЛ · l = eυBl. |
По определению ЭДС
В других неподвижных частях контура сторонняя сила равна нулю. Соотношению для инд можно придать привычный вид. За время Δt площадь контура изменяется на ΔS = lυΔt. Изменение магнитного потока за это время равно ΔΦ = BlυΔt. Следовательно,
Для того, чтобы установить знак в формуле, связывающей инд и нужно выбрать согласованные между собой по правилу правого буравчика направление нормали и положительное направление обхода контура как это сделано на рис. 1.20.1 и 1.20.2. Если это сделать, то легко прийти к формуле Фарадея.
Если сопротивление всей цепи равно R, то по ней будет протекать индукционный ток, равный Iинд = инд/R. За время Δt на сопротивлении R выделится джоулево тепло
Возникает вопрос: откуда берется эта энергия, ведь сила Лоренца работы не совершает! Этот парадокс возник потому, что мы учли работу только одной составляющей силы Лоренца. При протекании индукционного тока по проводнику, находящемуся в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, связанная с относительной скоростью движения зарядов вдоль проводника. Эта составляющая ответственна за появление силы Ампера . Для случая, изображенного на рис. 1.20.3, модуль силы Ампера равен FA = I B l. Сила Ампера направлена навстречу движению проводника; поэтому она совершает отрицательную механическую работу. За время Δt эта работа Aмех равна
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю. Джоулево тепло в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике. Следовательно, электрическое поле, порожденное изменяющимся магнитным полем, не является потенциальным. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 г.
Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея. Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной: в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца; в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
| Модель. Электромагнитная индукция |
| Модель. Опыты Фарадея |
| Модель. Генератор переменного тока |
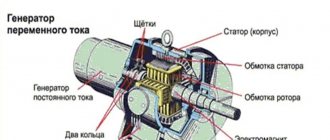
Вращающаяся катушка
Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).
Согласно формуле, на Ф воздействуют изменения в ситуациях:
- при изменении магнитного потока меняется вектор направления;
- изменяется площадь, заключенная в контур;
- меняется угол.
Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.
На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.
Где используются разные виды ЭДС
Перемещение проводника в магнитном поле применяют для генерации электроэнергии. Вращение ротора обеспечивают за счет разницы уровней жидкости (ГЭС), энергией ветра, приливами, топливными двигателями.
Принцип действия трансформатора
Различное количество витков (взаимоиндукцию) применяют для изменения нужным образом напряжения во вторичной обмотке трансформатора. В таких конструкциях взаимную связь увеличивают с помощью ферромагнитного сердечника. Магнитную индукцию применяют для возникновения мощной отталкивающей силы при создании ультрасовременных транспортных магистралей. Созданная левитация позволяет исключить силу трения, значительно увеличить скорость передвижения поезда.
ЭДС самоиндукции
При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.
В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:
Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.
Взаимоиндукция
Если собрать модуль из двух катушек, в определенных условиях можно наблюдать явление взаимной индукции. Элементарное измерение покажет, что по мере увеличения расстояния между элементами уменьшается магнитный поток. Обратное явление наблюдается по мере уменьшения зазора.
Чтобы находить подходящие компоненты при создании электрических схем, необходимо изучить тематические вычисления:
- можно взять для примера катушки с разным количеством витков (n1 и n2);
- взаимоиндукция (M2) при прохождении по первому контуру тока I1 будет вычислена следующим образом:
M2 = (n2 * F)/ I1
- после преобразования этого выражения определяют значение магнитного потока:
F = (M2/ n2) *I1
- для расчета эдс электромагнитной индукции формула подойдет из описания базовых принципов:
E2 = — n2 * ΔF/ Δt = M 2 * ΔI1/ Δt
При необходимости можно найти по аналогичному алгоритму соотношение для первой катушки:
E1 = — n1 * ΔF/ Δt = M 1 * ΔI2/ Δt.
Следует обратить внимание, что в этом случае значение имеет сила (I2) во втором рабочем контуре.
Совместное влияние (взаимоиндукцию – М) рассчитывают по формуле:
M = K * √(L1 * l2).
Специальным коэффициентом (K) учитывают действительную силу связи между катушками.