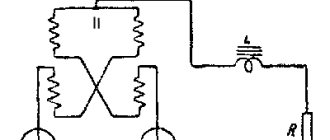
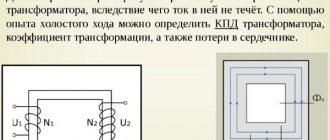
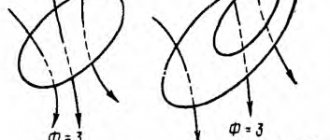Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.
Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.
Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:
- токи в обмотках;
- уровень намагниченности магнитопровода;
- магнитные характеристики сердечника;
- взаимодействие между соседними обмотками;
- наличия постоянной составляющей тока.
Конструкция и принцип действия силового трансформатора
В основе конструкции любого трансформатора находятся следующие элементы:
- Сердечник из ферромагнитного материала.
- Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.
В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.
Принцип работы:
- в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
- под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
- в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.
ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.
Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.
Глава четырнадцатая СХЕМА ЗАМЕЩЕНИЯ ТРАНСФОРМАТОРА И ЕЕ ПАРАМЕТРЫ
§ 14-1. Индуктивности обмоток трансформатора и электромагнитное рассеяние
Индуктивности обмоток.
В трансформаторах со стальным сердечником магнитная проницаемость стали ц. во время цикла пере-магничивания непостоянна. Поэтому в течение этого цикла непостоянны также собственные
L
и взаимные
М
индуктивности обмоток трансформатора. В результате такого непостоянства
ц,
при подключении трансформатора к сети с синусоидальным напряжением в его намагничивающем токе f’o возникают высшие гармоники (см. § 13-1).
При работе трансформатора на ток i0
накладывается ток нагрузки, по отношению к которому ток j0 и, в особенности, его высшие гармоники малы. Поэтому при исследовании режимов работы трансформатора указанными гармониками можно пренебречь и учитывать только основную гармонику тока /0- Это равносильно
допущению, что во время цикла перемагничивания ц, L
и
М
постоянны. Влияние насыщения сердечника при этом можно учесть, принимая в расчет при разных режимах работы трансформатора, при разных амплитудах потока сердечника, значения (д,,
L
и
М
для данного режима работы. В соответствии с изложенным будем полагать, что
ц, L
и
М
постоянны.
Рассмотрим индуктивности и индуктивные сопротивления обмоток, обусловленные магнитным потоком сердечника Фс, все силовые линии которого полностью замыкаются по замкнутому сердечнику и поэтому сцепляются со всеми витками первичной и вторичной обмоток (рис. 14-1).
Картина магнитного поля, замыкающегося целиком по сердечнику, одинакова независимо от того, какой из обмоток это поле создается. Поэтому и магнитное сопротивление -потоку Фс одинаково для поля обеих обмоток и в равенства (14-4), (14-5) и (14-6) входит одинаковая величина /?цС. Вследствие этого также
Первые слагаемые равенств (14-9) и (14-10) значительно больше вторых, так как потоки через воздух относительно малы.
Понятие об электромагнитном рассеянии. Полнота электромагнитной связи двух индуктивно связанных цепей характеризуется коэффициентом связи этих цепей
Как известно из курса теоретических основ электротехники, в реальных условиях всегда с
< 1.
Если бы в трансформаторе отсутствовали потоки Фв1 и Фв2, замыкающиеся по воздуху, то Lu —
Lcl, L22 = Lc2,
M —
Me, и в этом случае в соответствии с равенствами (14-4), (14-5), ^14-6) и (14-11)
Таким образом, неполнота электромагнитной связи в трансформаторе, выражаемая неравенством с < 1, обусловлена наличием потоков Фв1 и Фн2 или, точнее, неодинаковым их сцеплением с обеими обмотками. Условие с
— 1 было бы достигнуто только в том случае, если бы удалось полностью совместить первичную и вторичную обмотки» что фактически невозможно.
Явление неполной электромагнитной связи называется электромагнитным рассеянием.
Наряду с соотношением (14-11) целесообразно ввести в рассмотрение коэффициент электромагнитного рассеяния
Чем меньше с
и чем больше
а,
тем больше рассеяние.
Ввиду того что явление рассеяния обусловлено неодинаковостью или неполнотой сцепления потоков Фв1 и Фв2, проходящих по воздуху, с обеими обмотками, эти потоки называют часто также потоками рассеяния, однако это название до некоторой степени условно, так как потоки Фв1 и Фв2 обусловливают также явление взаимной индукции, поскольку Мв Ф
0. Как, будет выяснено ниже, степень неполноты электромагнитной связи, или величина электромагнитного рассеяния, оказывает большое влияние на многие
технические показатели и характеристики трансформаторов и вращающихся электрических машин.
В трансформаторах с ферромагнитным сердечником потоки ФВ1 и Фв2 относительно малы.
I Поэтому электромагнитная связь в трансформаторах весьма высока, а рассеяние мало.
В силовых трансформаторах, например, с
= 0,998 -*- 0,9995 и соответственно о = 0,001 ч- 0,004.
Вследствие этого значение а,
определяемое по формуле (14-12), представляет собой разность весьма близких величин и вычисление а по этой формуле связано с весьма большими погрешностями, так как
Ln, L%%
и
М в
практических устройствах не могут быть рассчитаны или определены из опыта с досхаточ-ной степенью точности. Поэтому возникает необходимость в непосредственном определении параметров, характеризующих электромагнитное рассеяние.
§ 14-2. Уравнения напряжения трансформатора
Рабочий процесс трансформатора можно исследовать на основе уравнений напряжения его обмоток.
Емкостные токи между элементами обмоток (витки и катушки) и между обмотками и сердечником трансформатора в обычных условиях работы трансформаторов (f
< 1000 -f- 5000
гц)
весьма малы, и ими можно пренебречь. В трансформаторах без ферромагнитного сердечника
Ln,
L22 и
М
постоянны. В соответствии с изложенным в § 14-1 можно принять, что эти величины постоянны также для любого рассматриваемого режима работы трансформатора со стальным сердечником. Пренебрежем сначала магнитными потерями в сердечнике. Тогда для однофазного двухобмо-
точного трансформатора (рис. 14-2) действительны следующие уравнения напряжения в дифференциальной форме:
Рис. 14-2. Схема однофазного двухобмоточного трансформатора
Здесь иъ и.2, ilt i2
— мгновенные значения напряжения и тока первичной и вторичной обмоток;
гх, г.г, Lu,
L22 — активные сопротивления и собственные индуктивности обмоток;
М
— взаимная индуктивность обмоток.
На схеме рис. 14-2 указаны положительные направления и
и
i,
причем стрелка
и
направлена от точки с высшим потенциалом к точке с низшим потенциалом.
При составлении уравнений (14-13) первичная обмотка рассматривается как приемник, а вторичная — как источник электрической энергии, и сами эти уравнения истолковываются следующим образом.
Первичное напряжение их
является приложенным, расходуется на падение напряжения г^ и уравновешивание э. д. с. первичной обмотки
и состоит поэтому из двух составляющих: rxix
и —
ех,
что и выражается первым уравнением (14-13). Вторичное напряжение
и%
возникает вследствие индуктирования-во вторичной обмотке э. д. с.
что соответствует второму уравнению (14-13). В уравнениях (14-13) считается, что М
> 0 и положительные токи
ix
и
i2
создают в сердечнике потоки одинакового направления.
Отметим, что в правой части второго уравнения (14-13) можно было бы изменить знаки на обратные. Тогда и2 следовало бы трактовать как напряжение, приложенное к вторичной обмотке со стороны вторичной сети. Некоторые, в особенности иностранные, авторы применяют также и эту последнюю форму записи.
Обычно силовые трансформаторы, а также ряд видов специальных трансформаторов работают с синусоидально изменяющимися токами и напряжениями. В этом случае вместо дифференциальных Уравнений (14-13) удобнее пользоваться комплексными уравнениями Для действующих значений токов и напряжений. Для получения этих уравнений в уравнения (14-13) следует подставить
xn — (nLu; xn
= col22; дг12 = соМ (14-15)
представляют собой полные собственные и взаимные индуктивные сопротивления обмоток.
При симметричной нагрузке трехфазных трансформаторов электромагнитные процессы протекают во всех фазах одинаково и соответствующие электромагнитные величины в каждой фазе также-одинаковы и лишь сдвинуты по фазе на 120°. Некоторая несимметрия магнитной цепи трехстержневого трансформатора, а также появление в ряде случаев (см. § 13-1) третьих гармоник потока обычно нет оказывают заметного влияния на работу трансформатора под’ нагрузкой. К тому же эти .явления при необходимости можно учесть отдельно. По этим причинам уравнения (14-14) с большой точностью* применимы также для фазных величин трехфазного трансформатора при симметричной его нагрузке. Система уравнений (14-14)- не учи* тывает лишь потерь в стали сердечника трансформатора. Учет этиэ* потерь будет рассмотрен отдельно.
Для трехфазного трансформатора в соответствии со сказанным выше 0it U2,
/х и /2 представляют собой фазные значения напряжений и токов.
Уравнения (14-13) и (14-14) полностью определяют процессы происходящие в трансформаторе при указанных выше допущениях и позволяют решать задачи, связанные с работой трансформатора Например^если определить из первого уравнения (14-14) /хи под ставить его значение во второе уравнение (14-14), то получим зав» симость вторичного напряжения 0%
от тока нагрузки
1г:
а второй член — падение напряжения на вторичных зажимах npij нагрузке.
Из этих соотношений видно, что такие важные с эксплуатационной точки зрения величины, как падение напряжения и ток короткого замыкания, определяются небольшой долей а
полного индуктивного сопротивления дг22, обусловленной электромагнитным рассеянием. Это же можно сказать и о ряде других величий, характеризующих эксплуатационные свойства трансформаторов и вращающихся электрических машин. Поэтому определение величин, характеризующих электромагнитное рассеяние, составляет важную задачу теории электрических машин.
Кроме указанных соображений о точности результатов, расчеты на основе уравнений (14-13) и (14-14) неудобны также в связи с тем, Что ввиду неравенства чисел витков (w1 Ф
до2) параметры
rlt
г2,
Ъп,
L22,
М, хп,
х22 и
х12,
а также напряжения
иъ и2, Ult U.z
и токи i2, /1( /2 сильно различаются по величине.
В связи с изложенным теорию электрических машин в отношении рассматриваемых вопросов целесообразно развить в следующих тесно связанных друг с другом направлениях:
1. Индуктивно связанные обмотки приводятся путем-соответствующих пересчетов к одинаковому числу витков, е результате чего порядки напряжений, токов и параметров этих обмоток становятся соответственно одинаковыми.
2. Из полных собственных индуктивностей Ln,
/_22 и индуктивных сопротивлений самоиндукции
хп
и х22 выделяются составляющие — индуктивности рассеяния
Si}
S2 и индуктивные сопротивления рассеяния
хх
и
х%,
обусловленные явлением электромагнитного рассеяния, причем это выделение производится с таким расчетом, что остающиеся части полных индуктивностей (Lu —
Si,
L22 — S2) и индуктивных сопротивлений
(хц
—
хи Х22
—
хй)
соответствуют индуктивно связанным цепям с полной связью
(с =
1).
3. Разрабатываются непосредственные методы расчета малых параметров — индуктивностей и индуктивных сопротивлений рассеяния — независимо от расчета полных индуктивностей и индуктивных сопротивлений, чем достигается необходимая точность в определении этих малых параметров.
4. От электрических цепей с индуктивной связью делается переход к схемам замещения с электрической связью цепей, что приводит к упрощению расчетов и большей наглядности теории.
5. Индуктивности и индуктивные сопротивления рассеяния вводятся в явном виде в расчетные соотношения и схемы замещения, что позволяет с необходимой точностью рассчитывать величины, зависящие от электромагнитного рассеяния.
Эти вопросы применительно к трансформаторам рассматриваются ииже.
§ 14-3. Схемы замещения двухобмоточного трансформатора
Приведение вторичной обмотки к первичной.
Первичные и вторичные токи, напряжения и другие величины имеют одинаковый порядок, если у первичной и вторичной обмоток число витков одинаково. Рассмотрим поэтому вместо реального трансформатора эквивалентный ему так называемый приведенный трансформатор, первичные и вторичные обмотки которого имеют одинаковое число витков.
Представим себе, что реальная вторичная обмотка трансформатора с числом витков ш2 заменена воображаемой, или приведенной,
обмоткой с числом витков w\ — Wx.
При этом число витков вторичной обмотки изменится в
раз. Величина k
называется коэффициентом приведения или трансформации.
В результате такой замены, или приведения, э. д. с. Е’2
и напряжение
U2
приведенной обмотки также изменяются в
k
раз по сравнению с величинами £2 и
U2
реальной вторичной обмотки:
Чтобы мощности приведенной и реальной обмоток при всех режимах работы были равны, необходимо соблюдать равенство
где 1’%
— приведенный вторичный ток. Отсюда с учетом второго равенства (14-21) следует, что
Намагничивающие силы приведенной и реальной обмоток на основании выражений (14-20) и (14-22) равны:
/>; = /аш2. (14-23)
Для того чтобы электромагнитные процессы в реальном и приведенном трансформаторах протекали одинаково, приведенная и реальная вторичные обмотки должны создавать одинаковые магнитные поля. Для этого, кроме соблюдения условия (14-23), необходимо, чтобы приведенная вторичная обмотка имела те же геометрические размеры и конфигурацию и была расположена в окне сердечника трансформатора так же, как и реальная вторичная, обмотка (см. например, рис. 12-2, 12-26). Поэтому суммарное сечение всех витков приведенной обмотки должно быть таким же, как и у реальной обмотки, а сечение каждого витка приведенной обмотки должно уменьшиться в k
раз. Но поскольку приведенная обмотка имеет в
k
раз больше витков, то в итоге активное сопротивление приведенной обмотки в
k2
раз больше, чем реальной:
Так как при одинаковых геометрических размерах и одинаковом расположении катушек их индуктивности и индуктивные сопротивления пропорциональны квадратам чисел витков, то между индуктивными сопротивлениями приведенной обмотки х’3
и реальной лг2 существует такое же соотношение:
Таким образом, все энергетические и электромагнитные соотношения в приведенном и реальном трансформаторах одинаковы, что и позволяет производить указанное приведение.
Схема замещения без учета магнитных потерь.
В соответствии с изложенным сделаем в уравнениях напряжения трансформатора (14-14^ поястановки:
При переходе к электрической связи двух цепей в соответствующей схеме замещения должна появиться общая для обеих цепей ветвь, которая обтекается суммой токов обеих цепей /г + 1[.
Соответственно этому в уравнениях напряжений этих цепей должны появиться одинаковые члены с множителями (/х + /J). Из уравнений (14-27) видно, что для получения в них таких членов нужно прибавить к первому из этих уравнений и вычесть из него член
]кхп!г
и прибавить ко второму и вычесть из него член
]кхп{‘%.
При этом получим
Введем следующие наименования и обозначения:
1) приведенное активное сопротивление вторичной обмотки
Уравнениям (14-34), как нетрудно видеть, соответствует схема замещения рис. 14-3, а.
Действительно, мысленно обойдя левый и правый контуры схемы рис. 14-3,
а
и составив уравнения напря-жеяия для этих контуров, вновь получим уравнения (14-34). Таким образом, схема рис. 14-3, а представляет собой схему замещения трансформатора, л^ответст^ующую уравнениям (14-14) и (14-34).
Аналогичным образом можно также преобразовать уравнения напряжения в дифференциальной форме (14-13), произведя в них подстановки
При этом получается схема замещения рис. 14-3, б,
где
представляют собой индуктивности рассеяния первичной и вторичной обмоток, а
— приведенную взаимную индуктивность.
Схема замещения рис. 14-3, б
действительна при любых закономерностях изменения напряжения и токов во времени, в том
числе и в случае переходных процессов.
Уравнения (14-34) и схемы замещения рис. 14-3 можно трактовать таким образом, что сопротивления гх
и
хъ г’ъ
и
х\
или индуктивности
St
и Sj включены в цепи дбмоток до и после трансформатора, а параметры обмоток трансформатора уменьшены на эти величины. В результате получается идеальный трансформатор, активные сопротивления которого равны нулю, а коэффициент электромагнитной-связи с = 1. Действительно, у такого идеального трансформатора приведенные собственные и взаимные индуктивные сопротивления одинаковы и равны
х’п
=
kxn
и поэтому в соответствии с равенствами (14-12) и (14-19) с2 = 1 и
а
= 0.
Рис. 14-3. Схемы замещения двух-
обмоточного трансформатора без
учета магнитных потерь
Отметим, что, как следует из рассмотрения приведенных преобразований, соотношения (14-26) и все последующие, а также схемы замещения рис. 14-3 справедливы и правильно отражают все процессы в трансформаторе при любом значении k.
С математической точки зрения эти преобразования означают переход от переменных /72 и /2 к новым переменным
О’2я 1’2
по формулам (14-26), что возможно при любом значении
k.
В связи с этим необходимо подчеркнуть, что индуктивные сопротивления и индуктивности рассеяния, согласно равенствам (14-30) — (14-33), (14-36), (14-37) и (14-38), определяются неоднозначно и зависят от коэффициента приведения
к.
Однако для силовых трансформаторов
k
рационально определять по формуле (14-20), как это и принято на практике и всюду в данной книге. Выбор иного значения
k
целесообразен лишь в специальных случаях, например в измерительных трансформаторах тока *.
Параметры схемы замещения.
Рассмотрим параметры схем замещения рис. 14-3 при
k
=
wjw2
[см. равенство (14-20)].
Приведенная взаимная индуктивность на основании равенств (14-6), (14-10) и (14-38)
Следовательно, сопротивление х’п
с большой точностью равно сопротивлению самоиндукции первичной обмотки от потока, замыкающегося по сердечнику.
1 А. И. Воль дек. О
схеме замещения трансформатора и ее параметрах. «Электричество», 1952,
№.
8, с. 21-25.
Ветви 1
—
2
схем замещения рис. 14-3 называются намагничивающими ветвями. Протекающий по этим ветвям намагничивающий то«
Таким образом, индуктивности рассеяния Slt
52 и Sj и индуктивные сопротивления рассеяния
Однако вторыми членами равенств (14-42) и (14-43) по сравнению с первыми пренебречь нельзя, и поэтому потоки, замыкающиеся по воздуху, можно назвать потоками рассеяния лишь условно.
Схема замещения с учетом магнитных потерь.
Потери в стали сердечника рвг при заданной частоте пропорциональны следующим величинам:
Таким образом, потери #вг пропорциональны квадрату напряжения Un
на зажима*
1
—2 намагничивающей цепи схемы замещения рис. 14-3,
а.
Если к этим зажимам параллельно
х’п
=
хс1
подключить активное сопротивление гмг, как показано на рис. 14-4,
а,
Величину рят
при заданной а. д. с.
Ех
можно считать известной из расчетных (см. § 13-2) ил.и опытных данных. Тогда можно считать известным- также гмг.
Намагничивающий ток
разделяется в двух ветвях намагничивающей цепи (рис. 14-4, а) на активную /ма и реактивную 1ЯГ
составляющие (см. § 13-2), из которых первая определяет мощность магнитных потерь, а вторая создает поток сердечника.
то потери в этом сопротивлении также будут пропорциональны (7i3. Величину сопротивления гмг можно подобрать так, чтобы потери в нем равнялись магнитным потерям:
Рис. 14-4. Намагничивающая цепь схемы замещения с учетом магнитных потерь
Схема с двумя параллельными ветвями намагничивающей цепнг хорошо согласовывается с реальными физическими явлениями. Однако расчеты на основе схемы замещения вести удобнее, если объединить две параллельные ветви схемы рис. 14-4, а
в одну общую ветвь, как показано на рис. 14-4,
б.
Тогда сопротивление этой ветви
Ф
При увеличении насыщения сердечника, т. е. при увеличении , Ei
или
Ult
сопротивление
х’п
при / = const уменьшается. Однако
при этом гмг«=! const, а значение гм уменьшается.
Схема замещения трансформатора с учетом магнитных потерь согласно рис. 14-4, б
показана нд рис. 14-5,
а.
Если использовать обозначения
то схему замещения можно изобразить более компактно, как пока’ зано на рис. 14-5,6. В_режиме холостого хода /а = 0 и Д = /н — току холостого хода трансформатора. В итоге получилась весьма простая Г-образная схема замещения трансформатора, представляющая собой пассивный четырехполюсник. Сопротивление намагничивающей цепи этой схемы ZM отражает явления в ферромагнитном сердечнике. Оно значительно больше сопротивлений Zx
и
Ъ’г,
которые включают в себя активные сопротивления и индуктивные сопротивления рассеяния обмоток. Для силовых трансформаторов в относительных единицах
Рис. 14-5. Схема замещения друх-обмоточного трансформатора с учетом магнитных потерь
Уравнения напряжений и схему замещения трансформатора можно представлять также в относительных единицах. Имея в виду, что
левые части уравнений вида (14-34) можно разделить на £/,,, а правые части — на ZH/H, в результате чего и будет совершен переход к относительным единицам. Абсолютные значения U, I, r, x
и Z в схемах замещения также можно заменить относительными. При этом расчеты режимов работы трансформатора можно вести в относительных единицах.
Нетрудно видеть, что относительные величины сопротивлений, токов и напряжений вторичной цепи будут зависеть от того, какая величина коэффициента k
была использована при приведении вторичной обмотки к первичной. Неопределенность в этом вопросе исчезает, если определять
k
всегда одинаковым образом. Например, в силовых трансформаторах всегда берут
к =
шх/а>а.
Упрощенная схема замещения.
Так как 2М >>
1Хта Z’%,
то во многих случаях можно положить 2М = оо, что означает разрыв намагничивающей цепи схемы замещения рис. 14-5. При ZM = оо будет /м = 0, т. е. такое допущение эквивалентно пренебрежению намагничивающим током или током холостого хода, что ввиду малости /м во многих случаях допустимо. При этом
1г =
—
l’t — t.
При
2М = оо и /м = 0 схема замещения принимает вид, изображенный на рис. 14-6. Параметры этой схемы
называются соответственно полным, активным и индуктивным сопротивлениями короткого замыкания (см. также § 14-5). Такие названия обусловлены тем, что замыкание вторичных зажимов трансформатора накоротко соответствует замыканию накоротко вторичных (правых) зажимов схемы замещения рис. 14-6 и при этом сопротивление трансформатора при коротком замыкании будет равным ZK.
Схема замещения рис. 14-6 чрезвычайно проста. Согласно этой схеме, трансформатор эквивалентен сопротивлению ZK. Обычно в силовых трансформаторах гк* = 0,05 -г- 0,15.
§ 14-4. Расчетное определение параметров схемы замещения трансформатора
Параметры схемы замещения могут быть определены расчетным или опытным путем.
Активные сопротивления обмоток легко рассчитываются по обмоточным данным, если известны коэффициенты вытеснения тока, учитывающие увеличение активных сопротивлений под влиянием
Рис. 14-6. Упрощенная схема замещения трансформатора
поверхностного эффекта (см. § 12-3). Обычно эти коэффициенты находятся в пределах 1,005—1,15.
Параметры намагничивающей цепи,легко определяются по данным расчета магнитной цепи (см. § 13-2). Сопротивление гмг для схемы рис. 14-4, а
уже было определено в § 14-3 [см. формулу (14-45)].
Для того чтобы найти х’и
для заданного значения э. д. с.
Ег
[см. формулу (12-3)1, надо определить поток Фс, затем н. с.
F
и, наконец, по формулам (13-3) или (13-6) ток
1Ог,
Тогда
После этого могут быть использованы формулы (14-46) и (14-47).
Метод противовключения. Наибольшую трудность вследствие сложного характера магнитных полей в воздухе представляет определение индуктивных сопротивлений рассеяния xt
и
х[.
Вместе с тем достаточно точное определение этих параметров имеет важное значение (см. § 14-1). Рассматривая схему замещения рис. 14-5, а, можно отметить, что влияние параметров
хг
и
x’t
этой схемы на эксплуатационные показатели и характеристики трансформатора гораздо больше, чем влияние параметров намагничивающей цепа.
Для вычисления л?! и х’%
используется метод так называемого противовключения, который был предложен в 1909 г^ немецким электротехником В. Роговским и заключается в следующем.
Нслн питать трансформатор с первичной и вторичной сторон такими напряжениями Ut
и
Oit
что
IB связи с изложенным можно сказать, что в режиме противо-включения существуют только магнитные поля рассеяния.
Осуществление опыта противовключения при wt ф w2
в действительности практически невозможно, так как весьма трудно достичь соблюдения условия (14-50) с большой точностью. При небольшом нарушении этого условия в сердечнике возникает заметный поток Фс, сравнимый с потоками в воздухе Фв, и равенства (14-51) и (14-53) грубо нарушаются. Поэтому осуществление этого опыта на практике возможно только при изготовлении геометрически подобного макета исследуемого трансформатора с
wx
= ш2 или при замене вторичной обмотки приведенной. В этом случае опыт можно осуществить по схеме рис. 14-7. Идея метода противовключения
Рис. 14-7. Схема опыта противовключения
лежит в основе всех расчетных методов определения индуктивных сопротивлений рассеяния.
Расчет индуктивных сопротивлений рассеяния
по отдельности для каждой из обмоток представляет значительные трудности. Поэтому обычно рассчитывается сумма этих сопротивлений исходя из картины магнитного поля в режиме противовключения, когда
кЩ + кЩ
=
(h + i*) wx
= 0.
На рис. 14-8, а
изображены сечения концентрических обмоток, расположенных в окне трансформатора, и характер создаваемого им магнитного поля в режиме противовключения. Эту картину поля можно заменить слегка идеализированной (рис. 14-8,
б),
когда все магнитные линии направлены вертикально и их эквивалентная расчетная длина между ярмами
1а
несколько больше высоты обмотки /, т. е.
/, = //**, (14-54)
где kR
= 0,93 -г 0,98 представляет собой так называемый коэффициент Роговского.
Определим закономерность распределения напряженности поля вдоль координаты х
на рис. 14-8,
б.
Применим закон полного тока
для магнитной линии в зоне / (0<: х
«£бг). Для стали можно принять |ic = оо и, следовательно,
Нс
= 0. Поэтому круговой инте-
Рис. 14-8. Картины магнитных полей трансформатора в режиме противовключения
грал равен Нх11а,
а рассматриваемая магнитная линия сцепляется с током
График изменения Нх
вдоль координаты
х
изображен на рис. 14-9.
Установить на рис. 14-8 точную границу раздела магнитных линий, сцепляющихся с разными обмотками, затруднительно. Поэтому вычисление хх
и дг^ по отдельности невозможно. Однако можно вычислить сумму
хх
и
х’%
и тогда расположение этой границы не имеет значения и можно условно принять, что она проходит посредине области // на рис. 14-8,
б.
Пренебрежем изменением диаметра вдоль координаты х
и примем в расчет средний диаметр двух обмоток
Dcp.
Тогда элементарная магнитная трубка кольцевидного сечения в зоне / с координатой
х
заключает поток
Рис. 14-9. Кривая напряженности поля рассеяния Их
= /
(х)
сцепляется с количеством витков щ.
Поэтому на основании выражений (14-55) и (14-56) потокосцепление первичной обмотки
Пусть вторичная обмотка приведена к первичной. Тогда для нее аналогичным образом получим
Величина
называется также приведенной величиной зазора между обмотками. Из {
14-58) видна зависимость сопротивлений рассеяния от геометрических соотношений. Увеличение диаметра сердечника
Dc
при
Вс =
const приводит к увеличению потока сердечника пропорционально О’нк уменьшению
wl
и /. В результате сопротивление рассеяния уменьшается. Если при проектировании трансформатора заданной мощности сечение сердечника уже выбрано, то этим определяется также величина
Ос„,
количество витков
wx
и площади сечения обмоток /бх «=« /б2. Если при этом выбирать / больше, а бх и б2 меньше, то рассеяние будет уменьшаться, и наоборот.
Расстояние между двумя обмотками б выбирается исходя из условий электрической прочности и исключения пробоя обмоток в зависимости от их номинальных напряжений. С ростом номинальных напряжений б растет и соответственно увеличивается также рассеяние.
Формулы для расчета индуктивных сопротивлений рассеяния чередующихся обмоток могут быть получены аналогичным образом.
Выше был рассмотрен расчет магнитного поля и индуктивных сопротивлений рассеяния для простейшего трансформатора с обмотками простой формы и с равномерным распределением полного тока обмотки iw
вдоль стержня. В более сложных случаях соответствующие расчеты сильно усложняются.
Глубокие исследования магнитных полей и индуктивных сопротивлений рассеяния трансформаторов в СССР выполнены Г. Н. Петровым, Е. Г. Марквардтом, Э. А. Манькиным и др.
§ 14-5. Опытное определение параметров схемы замещения трансформатора
Опыт холостого хода.
Опытное определение параметров схемы замещения трансформатора производится по данным опыта холостого хода и короткого замыкания.
Схема опытов холостого хода однофазного (т = 1) и трехфазного (т = 3) двухобмоточных трансформаторов приведены на рис. 14-10. Первичная обмотка трансформатора подключается на синусоидальное напряжение, а вторичная обмотка разомкнута. Измеряются первичные напряжения Uo
=
Uw,
ток /0 =
1г
и мощность
Ро
=
Pi,
а также вторичное напряжение
Uw.
Из данных опыта для однофазного трансформатора определяются полное, активное и индуктивное сопротивления холостого хода:
Рис. 14-10. Схемы опытов холостого
х°Да однофазного (а) и трехфазного (б)
двухобмоточных трансформаторов
Для трехфазного трансформатора по показаниям трех амперметров и вольтметров определяются средние значения линейного тока /Ол и линейного напряжения 1/Ол,
а по показаниям ваттметров — мощность холостого хода трех фаз
Ро
=
Р’
+
Р»>
Физический смысл имеют только значения сопротивлений, рассчитанные для фазы обмотки. Поэтому необходимо принять во внимание схему соединения обмотки. В случае соединения первичной обмотки в звезду
Коэффициент трансформации трехфазного трансформатора может рассчитываться по фазным напряжениям (&) или по линейным напряжениям (&л). Для теории трансформатора имеет значение первое из указанных значений коэффициента трансформации.
Целесообразно определять относительные значения перечисленных сопротивлений:
Уравнению напряжения холостого хода (14-7U) соответствует векторная диаграмма холостого хода на рис. 14-11. На этой диаграмме для ее ясности падения напряжения rjQ
и
jxjo
изображены весьма большими. В действительности они составляют доли процента от
Uo,
поэтому ими можно пренебречь и положить
Uo
= = —£1. Вследствие преобладания индуктивного сопротивления при
Uo
=
UH
коэффициент мощности cos
0 «£ 0,1.
Так как гх
<^ гм, то потери холостого хода практически представляют собой потери в стали сердечника, включая потери от вихревых токов в стенках бака в режиме холостого хода.
Опыт холостого хода производят обычно для ряда значений Uo:
от
Uo
а* 0,3
Un
до
Uo
« 1,1 (/„и по полученным данным строят характеристики холостого хода, представляющие собой зависимости /0, jP0, 2о, r0, coscp0 от
Uo
(рис. 14-12). При увеличении
Uo
насыщение сердечника увеличивается, вследствие чего /0 растет быстрее
UQ.
Поэтому
z0
и
х0
с ростом
Uo
уменьшаются. Так как
Рп г^ Е2 ^ U2,
а
Ро
растет быстрее
Щ,
то
г0
с ростом
Uо
также . уменьшается. По характеристикам холостого хода устанавливаются значения соответствующих величин для
Uo
==
UH.
Опыт короткого замыкания производится по схемам рис. 14-13. Вторичные обмотки замыкаются накоротко, а к первичным обмоткам во избежание перегрева и повреждения трансформатора подводится пониженное напряжение с таким расчетом, чтобы ток находился в пределах номинального.
Полное zK, активное гк
и реактивное
хк
сопротивления короткого замыкания рассчитываются по формулам, аналогичным для случая холостого хода.
Для однофазного трансформатора
Для трехфазного трансформатора по показаниям приборов определяются средние значения линейного напряжения £/кл, линейного тока /кл и мощности короткого замыкания трех фаз Рк. При соединении первичной обмотки в звезду параметры короткого замыкания на фазу будут следующие:
Рис. 14-12. Характеристики холостого хода трансформатора с соединением обмоток Y/Yo,
240
кв • а,
3150/380
в,
замеренные со стороны НН
Рис. 14-13. Схемы опытов короткого замыкания однофазного (а) и трехфазного (б) явухобмоточных трансформаторов
Векторная диаграмма трансформатора при коротком замыкании с /к = /н изображена в двух видах на рис. 14-15, а, б.
Треугольник на рис. 14-15,
б
называется треугольником короткого замыкания. Его катеты представляют собой активную и реактивную составляющие напряжения короткого замыкания:
ика = ик
cos фк; MKr = uKsin
K. (14-79)
В трансформаторах мощностью SB =
10
кв -а
обычно cos
K « я» 0,65, а в трансформаторах мощностью SH = 60 000 кв -а
обычно cos фк « 0,05. Таким образом, в мощных трансформаторах преобладают составляющие
uv
и
х&
по сравнению с ыка и гк. Очевидно,
что мКо* = гк*,
«кг* = *к*- Величина
ика*
приводится к температуре обмоток, равной 75е С.
Согласно изложенному, напряжение короткого замыкания характеризует величину активных сопротивлений и индуктивных сопротивлений рассеяния трансформатора и является поэтому важной характеристикой трансформатора. Величина ико/о указывается в паспортной табличке трансформатора. В силовых трансформаторах ик%
= 4,5 -5- 15. Первая цифра относится к трансформаторам с номинальным линейным напряжением {/лн=^ 10 к», авто-рая — к трансформаторам с
Un,
н = 500 /се, которые обладают большим рассеянием вследствие большого расстояния между обмотками.
Величина э. д. с. Ег
в опыте короткого замыкания при ^к — ^н в 15—40 раз меньше [/„. При этом магнитные потери в 225—1600 раз меньше, чем в случае
U = UB,
и весьма малы. Поэтому мощность короткого замыкания
Рк
с большой точностью представляет собой мощность электрических потерь в обмотках, включая добавочные потери в стенках бака и в крепежных деталях от потоков рассеяния трансформатора. Следовательно, и
гк
— гх + г«, определенное из опыта короткого замыкания, является эквивалентным сопротивлением с учетом этих потерь.
Если короткое замыкание происходит при номинальном первичном напряжении, то
Рис. 14-14. Характеристики короткого замыкания трансформатора с соединением обмоток Y/Yo, 240 кв-а,
3150/380 в, замеренные со стороны ВН
Рис. 14-15. Векторные диаграммы трансформатора при коротком замыкании с /* = /„
Содержание Предыдущий § Следующий
Физическое понятие индуктивности обмоток
Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.
Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.
При постоянном токе говорить об индуктивности бессмысленно.
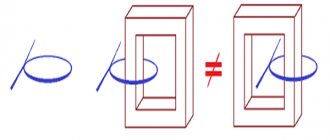
В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.
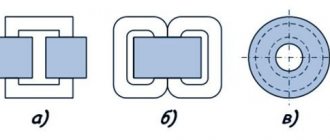
Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.
Формулы и измерение
Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:
- линейный проводник;
- одновитковая катушка;
- плоская катушка;
- соленоидальная обмотка;
- тороидальная форма.
Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.
В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.
Формулы для расчета индуктивности трансформатора основаны на расчетах соленоида:
L=µ0µN2S/l, где
µ0 – магнитная постоянная;
µ – магнитная проницаемость сердечника;
N – количество витков;
S – площадь одного витка;
l – длина обмотки.
Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.
В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.
Содержание
- 1. Общая часть
- 2. Определение нагрузки на трансформаторы тока для измерительных приборов
- 3. Определение напряжения на вторичной обмотке трансформатора тока
- 4. Определение нагрузки на трансформаторы тока для релейной защиты
- 5. Определение расчетной кратности (Красч.) для выбора допустимой нагрузки (Zдоп.) на трансформаторы тока по кривым предельных кратностей
- 5.1 Токовые защиты с независимой характеристикой
- 5.2 Токовые отсечки
- 5.3 Максимальные токовые защиты с зависимой характеристикой
- 5.4 Направленные токовые и дистанционные защиты
- 5.5 Дифференциальные токовые защиты
- 5.6 Дифференциально-фазные высокочастотные защиты
- 5.7 Продольные дифференциальные токовые защиты линий
- 6 Определение расчетной нагрузки Zн
- 7. Определение сопротивления соединительных проводов
- 8. Справочные данные по потреблению релейной аппаратуры
Как измерить в домашних условиях
Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.
Порядок действий следующий:
- При помощи омметра определяют активное сопротивление обмотки R.
- Подключают трансформатор последовательно с амперметром в сеть.
- Параллельно обмотке подключают вольтметр.
- По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
- Индуктивное сопротивление находят, вычитая из полного сопротивления активное: XL=Z-R
- Индуктивность определяется по формуле: L=XL/(2πf), где π – число пи 3.14, f – частота измерений.
Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.
Определение нагрузки на трансформаторы тока для релейной защиты
Нагрузка на ТТ для релейной защиты складывается из последовательно включенных сопротивлений релейной аппаратуры , соединительных проводов и переходных сопротивлений в контактных соединениях. Величина вторичной нагрузки зависит также от схемы соединения ТТ и от вида КЗ.
Релейная защита в условиях КЗ обычно работает при больших токах, которые во много раз превышают номинальный ток ТТ. Расчетами и опытом эксплуатации установлено, что для обеспечения правильной работы релейной защиты погрешности ТТ не должны превышать предельно допустимых значений.
По ПУЭ эта погрешность, как правило, не должна быть более 10%.
В ГОСТ 7746-88 точность ТТ, используемых для релейной защиты, нормируется по их полной погрешности (ε), обусловленной током намагничивания. По условию ε < 10% построены кривые предельных кратностей ТТ.
При этом наибольшее отношение первичного тока к его номинальному значению, при котором полная погрешность при заданной вторичной нагрузке не превышает 10%, называется предельной кратностью (К10).
Согласно тому же ГОСТ заводы-поставщики ТТ обязаны гарантировать значение номинальной предельной кратности (К10н), при которой полная погрешность ТТ, работающего с номинальной вторичной нагрузкой, не превышает 10%.
Чтобы найти допустимую нагрузку по кривым предельных кратностей, необходимо предварительно определить расчетную кратность тока К.З., т. е. отношение тока КЗ в расчетной точке к минимальному току ТТ (Красч.)