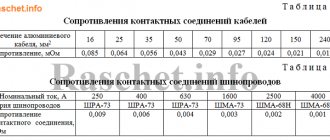
Всем доброго времени суток! В прошлой статье я рассказал о дросселях сглаживающих фильтров и изложил принцип их расчёта. Однако такие типы дросселей в бытовой технике применяются не очень часто, так как в маломощных устройствах зачастую эффективнее использовать ёмкостные фильтры. Наиболее часто в электронных устройствах применяют другой вид дросселей – дроссели переменного тока. Об их особенностях, принципах работы и расчёте параметров таких дросселей пойдёт речь в этой статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Особенности работы дросселя переменного тока
Дроссель переменного тока, так же как и любой другой дроссель представляет собой катушку индуктивности с ферромагнитным сердечником. Данный тип дросселя включается последовательно с нагрузкой, аналогично сглаживающему дросселю, но в отличие от него, протекающий ток через дроссель переменного тока не имеет постоянного тока подмагничивания. В связи с этим дроссель переменного тока широко применяется в балластных и токоограничительных цепях, мощных антенных и фильтрующих устройствах, а так же в различных импульсных преобразователях напряжения.
В независимости от применения дросселя в схеме его работа основана на зависимости его реактивного сопротивления XL от частоты f протекающего через него тока IH и падении напряжения на дросселе UL
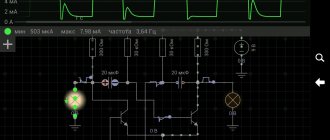
Дроссель переменного тока.
Таким образом, величина напряжения на дросселе UL определяется индуктивностью дросселя L и параметрами тока, протекающего через дроссель: частота тока f и значение тока в цепи IH.
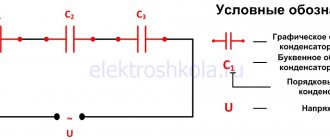
Параллельный колебательный контур.
Если соединить катушку индуктивности и конденсатор — получится очень интересный элемент радиотехники — колебательный контур. Если зарядить конденсатор или навести в катушке Э.Д.С., используя электромагнитное поле — в контуре начнут происходить следующие процессы: Конденсатор разряжаясь, возбуждает электромагнитное поле в катушке индуктивности. Когда заряд истощается, катушка индуктивности возвращает запасенную энергию обратно в конденсатор, но уже с противоположным знаком, за счет Э.Д.С. самоиндукции. Это будет повторяться снова и снова — в контуре возникнут электромагнитные колебания синусоидальной формы. Частота этих колебаний называется резонансной частотой контура, и зависит от величин емкости конденсатора(С), и индуктивности катушки (L).
Параллельный колебательный контур обладает очень большим сопротивлением на своей резонансной частоте. Это позволяет использовать его для частотной селекции(выделения) в входных цепях радиоаппаратуры и усилителях промежуточной частоты, а так же — в различных схемах задающих генераторов.
Влияние немагнитного зазора на дроссель
В предыдущих статьях я рассказывал о негативном влиянии насыщения сердечника на снижение магнитной проницаемости μe и индуктивности дросселя L, которые приводят к искажению формы тока протекающего через дроссель.
Форма тока, протекающего через дроссель: для ненасыщенного сердечника (1) и для насыщенного сердечника (2).
На данном рисунке изображено искажение формы тока синусоидального напряжения при работе дросселя на насыщенном и ненасыщенном участке кривой намагничивания. Степень искажения формы напряжения зависит также от отношения реактивного сопротивления дросселя к активному сопротивлению нагрузки XL/RH. То есть при насыщении сердечника, чем меньше данное соотношение, тем меньше степень искажения формы напряжения. Таким образом, введение немагнитного зазора кроме стабилизации величины индуктивности, в широких пределах изменения тока, позволяет пропустить через дроссель переменный ток без значительных изменений.
Кроме вышеописанных факторов, введение немагнитного зазора приводит к некоторым особенностям, которые необходимо учитывать при разработке и изготовлении дросселей с зазором. Основной особенностью является уширение магнитного потока в зазоре.
Уширение магнитного потока в немагнитном зазоре дросселя: стержень дросселя (слева) и его поперечное сечение (справа). Пунктиром обозначены размеры увеличенного сечения вследствие выпучивания магнитного потока.
Данное явление связанно с тем, что в дросселе с зазором магнитный поток выходит за пределы пространства, находящегося между двух концов разрезанного сердечника, поэтому площадь поперечного сечения в немагнитном зазоре как бы увеличивается.
Размеры уширения сечения зависит от длины обмотки дросселя lоб, площади сечения сердечника Se и длины немагнитного зазора lз. Уширение магнитного потока уменьшает магнитное сопротивление цепи и, следовательно, увеличивает индуктивность дросселя. Для учёта уширения магнитного потока и увеличения индуктивности вводится коэффициент выпучивания F, учитывающий уширение магнитного потока в немагнитном зазоре. Поэтому значение индуктивности дросселя будет определятся следующим выражением
где ω – количество витков провода в обмотке,
μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м,
μе – эквивалентная (относительная) магнитная проницаемость сердечника,
Sе – эквивалентная площадь поперечного сечения сердечника,
lе – эквивалентная длина магнитной линии сердечника.
lM – длина магнитной линии в сердечнике.
F – коэффициент, учитывающий уширение магнитного потока в зазоре.
Индуктивность двухпроводной линии
Двухпроводная линия (рис. 1.16, а) состоит из двух параллельных проводов одинакового радиуса г0, имеющих большую длину I по сравнению с расстоянием d между ними. Магнитная проницаемость материала проводов (г, окружающей среды — µ0. Токи I в прямом и обратном проводах отличаются лишь направлением; начало координат взято в центре сечения левого провода.
Для отдельного провода ввиду его осевой симметрии, при пренебрежении искажением поля у его концов, применение закона полного тока к окружности радиуса дает:
При интегрировании по окружности, лежащей внутри отдельного провода охватывается лишь часть LХ всего тока, протекающая внутри круга радиуса х, равная при равномерном распределении тока по сечению
В воздухе между проводами на линии, соединяющей центры их сечений направления полей, создаваемых обоими токами согласно правилу правого винта, совпадают и напряженности поля и индукции складываются:
Эти же формулы справедливы и для т. е. снаружи линии, но здесь они дают разность полей.
Внутри левого провода линии напряженность поля и индукция от обоих проводов будут:
Внутри правого провода соответственно,
На рис. 1.16, б представлено распределение напряженности поля и индукции вдоль оси х для магнитной проницаемости материала проводов µ > µ0. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.
На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,
Весь поток между проводами — внешний поток
одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому
а соответствующая ему внешняя индуктивность
Для большинства линий расстояние d между проводами значительно превышает радиус r0 проводов. В этом случае
Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r0 поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода
Так как поток dФi охватывает не весь ток, а только его часть [см. формулу (1.3)], элементарное потокосцепление
Весь поток между проводами — внешний поток
Соответственно, внутренняя индуктивность
Суммарная индуктивность линии
При медных или алюминиевых проводах () в большинстве случаев вторым членом можно пренебречь по сравнению с первым и тогда
Для стальных проводов () основной частью потока является внутренний поток и индуктивность
практически не будет зависеть от расстояния между проводами.
Принципы расчёта дросселей переменного тока
Расчёт дросселя переменного тока ведётся аналогично расчёту сглаживающего дросселя, но с учётом начальных условий. Так для дросселя переменного тока определяющими параметрами являются: требуемая индуктивность L, приложенное напряжение UL, частота переменного тока f, перегрев дросселя. Кроме этого необходимо определиться с материалом сердечника дросселя, который определят индукцию насыщения BS и максимальную индукцию в сердечнике Bm, которая для предотвращения насыщения сердечника выбирается из условия
В основе расчётов дросселя переменного тока лежит выражения для определения величина действующего напряжения падающего на дросселе UL
где f – частота переменного тока,
L – индуктивность дросселя,
I – действующее значение тока дросселя.
Тогда с учетом выражения для индуктивности дросселя с замкнутым сердечником и выражения для максимальной индукции в сердечнике напряжение на дросселе будет зависеть от следующих параметров
где μе – эквивалентная магнитная проницаемость сердечника,
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
ω – количество витков обмотки дросселя,
Se – эквивалентное сечение сердечника дросселя,
le – эквивалентная длина магнитного пути сердечника дросселя,
Bm – максимальное значение магнитной индукции сердечника,
ka – коэффициент амплитуды тока (напряжения) дросселя.
Получившееся выражение довольно часто можно встретить под названием основной формулы трансформаторной ЭДС, так как оно устанавливает однозначное соотношение, между ЭДС на зажимах обмотки и числом витков обмотки, при заданной величине магнитной индукции в сердечнике. Тогда при синусоидальном напряжении (коэффициент амплитуды ka ≈ 1,414) выражение принимает следующий вид
Вернёмся к исходному выражению для напряжения на дросселе UL, в котором неоднозначным является параметр – количество витков. Данный параметр кроме всего прочего (величины индуктивности L и магнитной проницаемости μе сердечника) зависит от размеров магнитопровода, а конкретнее от площади окна SO, которое можно вычислить по следующему выражению
где I – действующее значение тока дросселя,
ω – количество витков обмотки дросселя,
kИ – коэффициент использования окна сердечника,
j – плотность тока в проводе обмотки.
Параметры kИ и j выбирают аналогично, как и для дросселя сглаживающего фильтра, то есть коэффициент использования окна сердечника kИ ≈ 0,3, а плотность тока j = 5 А/мм2.
Тогда выражая из данного выражения количество витков провода ω, получим
Получившееся выражение определяет основное расчётное выражение для определения типоразмера сердечника – произведение площадей сердечника SeSO. После преобразования выражения для действующего напряжения на дросселе UL определяем количество витков обмотки ω и величину немагнитного зазора δ
где μе – эквивалентная магнитная проницаемость сердечника,
μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м,
Se – эквивалентное сечение сердечника дросселя,
le – эквивалентная длина магнитного пути сердечника дросселя,
Bm – максимальное значение магнитной индукции сердечника,
ka – коэффициент амплитуды тока (напряжения) дросселя.
Вычисленное количество витков является ориентировочным, так как из-за уширения магнитного потока значение индуктивности оказывается несколько больше при данном количестве витков, что в некоторых случаях является нежелательным. Поэтому необходимо пересчитать витки с учётом коэффициента уширения магнитного потока F
Осталось выбрать сечение обмоточного провода SП
где SO – площадь окна используемого сердечника,
kИ – коэффициент использования окна сердечника,
ω – количество витков обмотки дросселя.
Выбор сечения провода необходимо производить, округлив полученное значение до ближайшего номинала, при этом необходимо учитывать, что на высоких частотах возрастают потери мощности в проводе. Поэтому при достаточно высокой частоте необходимо использовать обмоточный провод, состоящий из нескольких жил, при этом диаметр жилы выбирают исходя из глубины скин-слоя δ
где f – частота переменного тока, протекающего через дроссель,
δ – толщина скин-слоя,
dп – диаметр жилы в обмоточном проводе.
После конструктивного расчёта сердечника и обмотки необходимо проверить тепловой режим работы дросселя – нагрев и перегрев дросселя.
Взаимоиндуктивность и ее расчет
Для двух контуров, имеющих w1 и w2 витков с токами I1 и I2 (рис. 1.17), поток первого контура, определяемый током этого контура, — поток самоиндукции Ф1l—может быть разложен на поток рассеяния Ф1s, пронизывающий только этот контур, и поток взаимоиндукции Ф1m, пронизывающий также и второй контур:
Потокосцепление, соответствующее потоку Ф11 (при условии, что этот поток пронизывает все витки первого контура, равно
а потокосцепление рассеяния
Аналогично для второго контура
Потокосцепление второго контура, определяемое током первого,
а потокосцепление первого контура, определяемое током второго,
Можно показать, что
Величина M называется взаимоиндуктивностью и определяется конфигурацией контуров, их взаимным расположением и магнитной проницаемостью среды. Взаимоиндуктивность также измеряется в генри (гн). Суммарный поток, пронизывающий первый контур,
Суммарное потокосцепление первого контура
и соответственно для второго контура
В этих алгебраических суммах первый член всегда положителен, а знак перед вторым членом определяется направлением токов в контурах; положительный знак соответствует случаю совпадения направлений потоков Ф1м и Ф2м (см. рис. 1.17). Из изложенного видно, что
Таким образом, взаимоиндуктивность и индуктивности всегда удовлетворяют неравенству
а используемый в технических расчетах коэффициент связи двух контуров
Аналогично, в системе многих контуров потокосцепление контура определяется токами всех контуров:
где Lq — индуктивность q-то контура, Мqp = Мрq — взаимоиндуктивность q- и р-го контуров. Общий прием расчета взаимоиндуктивности контуров заключается в нахождении потокосцепления, пронизывающего контур q, но созданного током р-го контура, и делении его на этот ток.
Как рассчитать межвитковую ёмкость обмотки дросселя?
В дросселе, между витками, слоями и металлическими предметами вокруг дросселя существует некоторая разность потенциалов, создающих электрическое поле. Для оценки влияния данного поля вводят понятие межвитковой ёмкости или собственной ёмкости дросселя, величина которой зависит от размеров и конструктивных особенностей дросселя.
Межвитковая ёмкость C обмотки, являясь паразитным параметром, совместно с индуктивностью рассеивания и собственной индуктивностью дросселя образуют различные виды фильтров и колебательных контуров. Хотя данный параметр имеет небольшое значение, тем не менее, в определённых условиях его приходится учитывать, однако точный расчёт затруднён в связи с большим влиянием различных конструктивных параметров, в первую очередь, взаимного расположения витков провода между собой. Так наибольшей межвитковой ёмкостью обладают катушки намотанные «внавал», а наименьшей – катушки с намоткой типа «Универсаль» или секционные катушки.
Межвитковую емкость Собщ дросселя можно представить в виде суммы емкостей между внутренним слоем обмотки и магнитопроводом С1 и межслоевой емкости внутри обмотки С2
Ёмкость между внутренним слоем обмотки и магнитопроводом можно определить из эмпирической формулы
где εа – абсолютная диэлектрическая проницаемость среды вокруг проводника, εа = ε0εr,
εr – относительная диэлектрическая проницаемость,
ε0 – электрическая постоянная, ε0 = 8,85 * 10-12 Ф/м,
r – радиус поперечного сечения провода,
а – расстояние между магнитопроводом и осью провода,
n – число витков в слое,
р1 – периметр витка внутреннего слоя обмотки.
Относительная диэлектрическая проницаемость берётся для материала каркаса дросселя, если бескаркасное исполнение, то соответственно проницаемость воздуха либо изоляции проводника, в зависимости от необходимой точности.
Емкость между слоя обмотки так же вычисляется по эмпирической формуле
где рср – периметр среднего витка обмотки,
b – расстояние между осями витков в соседних слоях,
m – число слоёв.
В данном случае диэлектрическая проницаемость берётся для материала межслоевой изоляции.
Во всех случаях необходимо добиваться уменьшения межвитковой ёмкости обмотки. Для этого применяют различные виды намоток и материалов для каркасов и межслоевой изоляции с малым значением диэлектрической проницаемости.
Взаимоиндуктивность двух параллельных двухпроводных линий
Пусть две параллельные двухпроводные линии расположены симметрично так, как это было показано на рис. 1.4. При условии d> г0 внутренним потоком в проводах по сравнению с внешним можно пренебречь. Магнитный поток, пронизывающий первую линию и созданный током I2 второй, может быть найден как сумма потоков, создаваемых каждым из проводов второй линии в отдельности. Тогда магнитный поток, пронизывающий первую линию,
расстояния от провода линии 1 до проводов линии 2 .
Магнитный поток Ф одновременно является потокосцеплением первой линии, так как сцепляется с ней один раз; поэтому
а взаимоиндуктивность
Для уменьшения коэффициента связи между линиями связи l и передачи 2 применяют транспозицию линии связи, заключающуюся в перекрещивании проводов линии связи через равные расстояния; тогда суммарное потокосцепление будет равно нулю.
Маркировка и обозначения
В принципиальных схемах и технической документации дроссели обозначаются латинской буквой L, условное графическое обозначение — в виде полуокружностей. Их количество нигде не указывается, но обычно не превышает трёх штук. Жирная точка, ставящаяся в начале полуокружностей, обозначает начало витков. Если индуктивность выполняется на каркасе, сверку изображения чертится прямая линия. Для обозначения номиналов элемента используется код из букв и цифр или цветовая маркировка.
Вам это будет интересно Как надавать первую медицинскую помощь при ударе током
Цифры указывают на значение индуктивности, а буква — на допуск. Например, код 250 J обозначает индуктивность, равную 25 мкГн с погрешностью в пять процентов. Когда на маркировке стоит только число, то это значит, что допуск составляет 20%. Таким образом, первые две цифры обозначают числовое значение в микрогенри, а третья — множитель. Буква D ставится на высокоточных изделиях, их погрешность не превышает 0,3%.
Цветовая маркировка, в принципе, соответствует буквенно-цифровой, но только наносится в виде цветных полос. Первые две указывают на значения в микрогенри, третья — коэффициент для умножения, а четвёртая — допуск. Индуктивность дросселя, на котором изображены две оранжевые полосы, коричневая и белая, равна 33 мкГ с разрешённым отклонением в 10%.
Дроссели сглаживающих фильтров питания
Основными параметрами дросселей сглаживающих фильтров питания являются индуктивность, номинальный ток подмагничивания, сопротивление постоянному току, допустимое переменное напряжение. Во многих случаях стремятся при заданных габаритных размерах и массе получить возможно большую (или заданную) индуктивность при минимальном сопротивлении постоянному току. Поскольку индуктивность дросселя зависит от тока подмагничивания и амплитуды переменного напряжения, ее измеряют при номинальном токе подмагничивания и заданном переменном напряжении. Расчет дросселей фильтров выпрямителей можно выполнять по методике, используемой для расчета согласующих трансформаторов с постоянным подмагничиванием.
Вернуться на главную страницу … | |