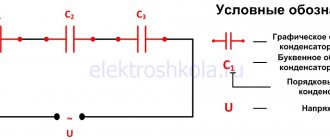
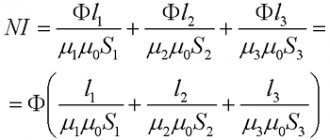Электрические цепи и их разновидности
Электрическая цепь представляет собой комплекс устройств и отдельных объектов, которые связываются заданным способом. Они обеспечивают путь для прохождения электротока. Для характеристики отношения заряда, протекающего в рамках каждого отдельного проводника за некоторое время, к продолжительности этого времени используется определенная физическая величина. И это сила тока в электрической цепи.
В состав такой цепи включены источник энергии, энергопотребители, т.е. нагрузка и провода. Они делятся на две разновидности:
- Неразветвленные – ток, движущийся от генератора к энергопотребителю, не меняется по своему значению. Например, это освещение, включающее в свой состав только одну лампочку.
- Разветвленные – цепи, имеющие некоторые ответвления. Ток, двигаясь от источника, разделяется и идет на нагрузку по нескольким ветвям. При этом его значение меняется.
Примером может служить освещение, включающее многорожковую люстру.
Ветвь являет собой один или несколько компонентов, соединенных последовательно. Движение тока идет от узла с высоким напряжением к узлу с минимальным его значением. При этом входящий ток на узле совпадает с выходящим.
Цепи могут быть нелинейными и линейными. Если в первых существует один и более элементов, где есть зависимость значений от тока и напряжения, то у вторых характеристики элементов не имеют такой зависимости. Кроме того, в цепях, характеризующихся постоянным током, его направление не меняется, а при условии переменного тока происходит его изменение с учетом параметра времени .
Задачи на правило Кирхгофа с решением
Как решать задачи по правилу Кирхгофа? Прежде, чем приступать к решению задач, обязательно изучите теорию. Также мы подготовили для вас универсальную памятку по решению физических задач.
Задача №1 на эквивалентные преобразования соединений проводников.
Условие
Преобразуйте схему с помощью эквивалентных преобразований.
Решение
Кроме основных формул для последовательного и параллельного соединения проводников, существуют формулы для преобразования звезды резисторов в эквивалентный треугольник и наоборот. Треугольник резисторов R2 R3 R4 можно преобразовать в эквивалентную звезду RB RB RD по формулам:
Преобразованная схема будет выглядеть следующим образом:
Ответ: см. выше.
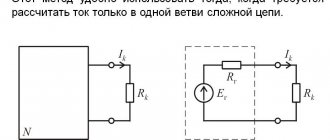
Правила Кирхгофа применяются для сложных цепей(например, для цепей с несколькими источниками питания), когда эквивалентные преобразования не приносят результата.
Задача №2 на первое правило (закон) Кирхгофа
Условие
Необходимо составить уравнения по первому закону Кирхгофа для следующей цепи:
Решение
В данной цепи 4 узла. По первому закону составляем 3 уравнения (на 1 уравнение меньше, чем количества узлов):
Ответ: см. выше.
Для решения задач на правила Кирхгофа необходимо уметь решать системы линейных уравнений. Для решения сложных систем удобно использовать специальные программы: MathCad, MatLab и т.д.
Далее для наглядности рассмотрим задачу с более простой схемой.
Задача №3 на правила Кирхгофа
Условие
Два источника питания E1=2В и E2=1В соединены по схеме, показанной на рисунке. Сопротивление R=5 Ом. Внутреннее сопротивление источников одинаково и равно r1=r2=1 Ом. Определить силу тока, который проходит через сопротивление.
Решение
По первому закону Кирхгофа сумма токов, сходящихся в узле, равна нулю (токи обозначим произвольно):
Выберем направление обхода верхнего контура против часовой стрелки. По второму закону Кирхгофа, сумма падений напряжений в контуре равна сумме ЭДС:
Запишем то же самое для второго контура, обходя его по часовой стрелке:
Объединим уравнения с неизвестными токами в систему:
Чтобы решить систему, выразим силу тока I1 из второго уравнения, а силу тока I2 – из третьего:
Первое уравнение теперь можно записать в виде:
Выражая искомый ток и подставляя значения из условия, получаем:
Ответ: 1,5 А.
Задача №4 на правила Кирхгофа
Условие
Дана схема электрической цепи. Необходимо:
- обозначить сопротивления, над каждой ветвью указать свой ток и источники ЭДС;
- указать на схеме направления токов и ЭДС;
- составить уравнения по первому и второму закону Кирхгофа.
Решение
Приведем схему, обозначив сопротивления, ЭДС и токи:
В схеме 7 токов и 4 узла. Необходимо составить 4 – 1 = 3 уравнения по первому закону Кирхгофа и 7 – 3 = 4 уравнения по второму закону Кирхгофа.
Первый закон Кирхгофа:
Второй закон Кирхгофа (выбранные контуры К1, К2, К3, К4 указаны на рисунке):
Ответ: см. выше.
Задача №5 на правила Кирхнофа
Условие
Определить все токи в ветвях, составив систему уравнений по законам Кирхгофа.
Параметры цепи: E1 = 40 В, E2 = 50 В, E3 = 60 В, R01 = 0,1 Ом, R02 = 0,3 Ом, R03 = 0,2 Ом, R1 = 4,4 Ом, R2 = 4,7 Ом, R3 = 4,6 Ом, R4 = 5,2 Ом, R5 = 7,6 Ом.
Решение
Направления токов в ветвях цепи и направления обхода контуров указаны на схеме. Цепь содержит 3 узла и 3 независимых контура. Таким образом, для расчета токов в ветвях необходимо составить два уравнения по первому закону Кирхгофа и три по второму:
Подставим числовые значения и решим систему уравнений:
Ответ: I1=10,68 А; I2=8,388 А; I3=7,192 А; I4=4,9 А; I5=2,292 А.
Сила тока и закон Ома
Осуществляя расчет силы тока цепи, следует помнить, что эта величина физического типа, демонстрирующая определенный заряд. Он протекает за некоторую временную единицу по проводнику. Базовая схема вычисления следующая:
I=q/t, где:
- I – сила электричества в Амперах (А) или Кл/с;
- q – заряд, перемещающийся в рамках проводника в Кулонах (Кл);
- t – время, затраченное на перемещение заряда, с.
В соответствии с положениями закона Ома для отдельной части цепи при вычислении силы тока применяется схема, показывающая:
- прямую зависимость силы тока от напряжения;
- взаимосвязь обратного типа с сопротивлением.
I=U/R, где:
- U – выраженное в вольтах напряжение, В;
- R – показатель сопротивления, Ом.
Отсюда будет следовать такая зависимость:
I = E/ R+r, где:
- Е – ЭДС, В;
- R – сопротивление внешнего типа, Ом
- r – сопротивление внутреннее, Ом
Воспользуйтесь другими онлайн калькуляторами:
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Главная → Примеры решения задач ТОЭ → Расчет электрических цепей постоянного тока методом эквивалентных преобразований Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Основными законами, определяющими расчет электрической цепи, являются законы Кирхгофа.
На основе законов Кирхгофа разработан ряд практических методов расчета электрических цепей постоянного тока, позволяющих сократить вычисления при расчете сложных схем.
Существенно упростить вычисления, а в некоторых случаях и снизить трудоемкость расчета, возможно с помощью эквивалентных преобразований схемы.
Преобразуют параллельные и последовательные соединения элементов, соединение «звезда» в эквивалентный «треугольник» и наоборот. Осуществляют замену источника тока эквивалентным источником ЭДС. Методом эквивалентных преобразований теоретически можно рассчитать любую цепь, и при этом использовать простые вычислительные средства. Или же определить ток в какой-либо одной ветви, без расчета токов других участков цепи.
В данной статье по теоретическим основам электротехники рассмотрены примеры расчета линейных электрических цепей постоянного тока с использованием метода эквивалентных преобразований типовых схем соединения источников и потребителей энергии, приведены расчетные формулы.
Решение задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Задача 1. Для цепи (рис. 1), определить эквивалентное сопротивление относительно входных зажимов a−g, если известно: R1 = R2 = 0,5 Ом, R3 = 8 Ом, R4 = R5 = 1 Ом, R6 = 12 Ом, R7 = 15 Ом, R8 = 2 Ом, R9 = 10 Ом, R10= 20 Ом.
Рис. 1
Решение
Начнем эквивалентные преобразования схемы с ветви наиболее удаленной от источника, т.е. от зажимов a−g:
Задача 2. Для цепи (рис. 2, а), определить входное сопротивление если известно: R1 = R2 = R3 = R4= 40 Ом.
Рис. 2
Решение
Исходную схему можно перечертить относительно входных зажимов (рис. 2, б), из чего видно, что все сопротивления включены параллельно. Так как величины сопротивлений равны, то для определения величины эквивалентного сопротивленияможно воспользоваться формулой:
где R – величина сопротивления, Ом;
n – количество параллельно соединенных сопротивлений.
Задача 3. Определить эквивалентное сопротивление относительно зажимов a–b, если R1 = R2 = R3 = R4 = R5 = R6 = 10 Ом (рис. 3, а).
Рис. 3
Решение
Преобразуем соединение «треугольник» f−d−c в эквивалентную «звезду». Определяем величины преобразованных сопротивлений (рис. 3, б):
По условию задачи величины всех сопротивлений равны, а значит:
На преобразованной схеме получили параллельное соединение ветвей между узлами e–b, тогда эквивалентное сопротивление равно:
И тогда эквивалентное сопротивление исходной схемы представляет последовательное соединение сопротивлений:
Задача 4. В заданной цепи (рис. 4, а) определить методом эквивалентных преобразований входные сопротивления ветвей a−b, c–d и f−b, если известно, что: R1 = 4 Ом, R2 = 8 Ом, R3 =4 Ом, R4 = 8 Ом, R5 = 2 Ом, R6 = 8 Ом, R7 = 6 Ом, R8 =8 Ом.
Решение
Для определения входного сопротивления ветвей исключают из схемы все источники ЭДС. При этом точки c и d, а также b и f соединяются накоротко, т.к. внутренние сопротивления идеальных источников напряжения равны нулю.
Рис. 4
Ветвь a−b разрывают, и т.к. сопротивление Ra–b = 0, то входное сопротивление ветви равно эквивалентному сопротивлению схемы относительно точек a и b (рис. 4, б):
Аналогично методом эквивалентных преобразований определяются входные сопротивления ветвей Rcd и Rbf. Причем, при вычислении сопротивлений учтено, что соединение накоротко точек a и b исключает ( «закорачивает») из схемы сопротивления R1, R2, R3, R4 в первом случае, и R5, R6, R7, R8 во втором случае.
Задача 5. В цепи (рис. 5) определить методом эквивалентных преобразований токи I1, I2, I3 и составить баланс мощностей, если известно: R1 = 12 Ом, R2 = 20 Ом, R3 = 30 Ом, U = 120 В.
Рис. 5
Решение
Эквивалентное сопротивлениедля параллельно включенных сопротивлений:
Эквивалентное сопротивление всей цепи:
Ток в неразветвленной части схемы:
Напряжение на параллельных сопротивлениях:
Токи в параллельных ветвях:
Баланс мощностей:
Задача 6. В цепи (рис. 6, а), определить методом эквивалентных преобразований показания амперметра, если известно: R1 = 2 Ом, R2 = 20 Ом, R3 = 30 Ом, R4 = 40 Ом, R5 = 10 Ом, R6 = 20 Ом, E = 48 В. Сопротивление амперметра можно считать равным нулю.
Рис. 6
Решение
Если сопротивления R2, R3, R4, R5 заменить одним эквивалентным сопротивлением RЭ, то исходную схему можно представить в упрощенном виде (рис. 6, б).
Величина эквивалентного сопротивления:
Преобразовав параллельное соединение сопротивлений RЭ и R6 схемы (рис. 6, б), получим замкнутый контур, для которого по второму закону Кирхгофа можно записать уравнение:
откуда ток I1:
Напряжение на зажимах параллельных ветвей Uab выразим из уравнения по закону Ома для пассивной ветви, полученной преобразованием RЭ и R6:
Тогда амперметр покажет ток:
Задача 7. Определить токи ветвей схемы методом эквивалентных преобразований (рис. 7, а), если R1 = R2 = R3 = R4 = 3 Ом, J = 5 А, R5 = 5 Ом.
Рис. 7
Решение
Преобразуем «треугольник» сопротивлений R1, R2, R3 в эквивалентную «звезду» R6, R7, R8 (рис. 7, б) и определим величины полученных сопротивлений:
Преобразуем параллельное соединение ветвей между узлами 4 и 5
Ток в контуре, полученном в результате преобразований, считаем равным току источника тока J, и тогда напряжение:
И теперь можно определить токи I4 и I5:
Возвращаясь к исходной схеме, определим напряжение U32 из уравнения по второму закону Кирхгофа:
Тогда ток в ветви с сопротивлением R3 определится:
Величины оставшихся неизвестными токов можно определить из уравнений по первому закону Кирхгофа для узлов 3 и 1:
Электронная версия статьи Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Примеры решения задач Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Расчет электрических цепей постоянного тока методом эквивалентных преобразований
Метод эквивалентных преобразований
02.09.2011, 303993 просмотра.
Добавить комментарий
Учебные материалы
Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю:
Согласно второму закону Кирхгофа алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.
Получить решение по ТОЭ
Расчет многоконтурной линейной электрической цепи, имеющей «b» ветвей с активными и пассивными элементами и «у» узлов, сводится к определению токов отдельных ветвей и напряжений на зажимах элементов, входящих в данную цепь.
Пассивной называется ветвь, не содержащая источника ЭДС. Ветвь, содержащая источник ЭДС, называется активной.
1-й закон Кирхгофа применяют к независимым узлам, т.е. таким, которые отличаются друг от друга хотя бы одной новой ветвью, что позволяет получить (y — I) уравнений.
Недостающие уравнения в количестве b — (у — I) составляют, исходя из второго закона Кирхгофа. Уравнение записывают для независимых контуров, которые отличаются один от другого, по крайней мере, одной ветвью.
Порядок выполнения расчета:
- выделяют в электрической цепи ветви, независимые узлы и контуры;
- с помощью стрелок указывают произвольно выбранные положительные направления токов в отдельных ветвях, а также указывают произвольно выбранное направление обхода контура;
- составляют уравнения по законам Кирхгофа, применяя следующее правило знаков:
- токи, направленные к узлу цепи, записывают со знаком «плюс», а токи, направленные от узла,- со знаком «минус» (для первого закона Кирхгофа);
- ЭДС и напряжение на резистивном элементе (RI) берутся со знаком»плюс», если направления ЭДС и тока в ветви совпадают с направлением обхода контура, а при встречном направлении — со знаком «минус»;
Отрицательные значения тока какой-либо ветви указывают на то, что выбранные ранее произвольные направления тока оказались ошибочными. Это следует учитывать, например, при построении потенциальной диаграммы, где следует знать истинное направление тока.
На рис. 4, а изображена исходная электрическая схема, для которой следует рассчитать токи в ветвях. Направления токов и обхода контуров приведены на рис. 4, б.
Рис.4
Система уравнений, составленных по первому и второму законам Кирхгофа, имеет вид
Дальше >Лекции по основам электротехники >
Последовательное соединение элементов
Общее сопротивление
Подобное включение подразумевает комбинацию деталей в прямой последовательности. Выход одного сопротивления подключается к входу другого. При этом отсутствуют какие-либо ответвления на участке. Величина тока, который проходит через все соединённые последовательно компоненты, будет одна и та же.
Внимание! Снижение потенциала на каждом резистивном элементе в сумме даст полное напряжение, приложенное к последовательной цепи.
Последовательное включение резисторов
В случае постоянного тока формула закона Ома для отрезка цепи имеет вид:
I = U/R.
Сила тока зависит от приложенного напряжения и оказанного ему сопротивления. Если выразить R, его формула:
R = U/I.
Параметры последовательной цепи, включающей n соединённых друг с другом элементов, имеют свои особенности.
Проходящий по цепи ток везде одинаковый:
I = I1= I2= … = In.
Прикладываемое напряжение является суммой напряжений на каждом резисторе:
U = U1 + U2+ … + Un.
Следовательно, рассчитать можно общее:
Rэкв.= U1/I + U2/I + … +Un/I) = R1 + R2 + … +Rn.
Важно! Последовательная цепь, имеющая в своём составе N резисторов равного номинала, имеет эквивалентное сопротивление Rэкв. = N*R.
Расчёт при смешанном соединении устройств
Сопротивление резистора — формула для рассчета
Произвести расчет сопротивления цепи, когда она разветвлена и наполнена разными видами резистивных соединений, просто не получится. Затрудняет решение задачи множество участков, где детали подключены друг другу в разных комбинациях. В таких обстоятельствах желательно выполнять ряд преобразований, добиваясь упрощения схемы вводом отдельных эквивалентных элементов. Выявляют при этом подходящие контуры последовательных и параллельных присоединений.
Например, выискав некоторое количество последовательных подключений резисторов, заменяют их на один эквивалентный компонент. Определив элементы, соединённые последовательно, также рисуют вместо него эквивалент. Вновь начинают искать подобные простые соединения.
Метод называют «методом свёртывания». Схему упрощают до тех пор, пока в ней не останется одно Rэкв.
Способ расчёта при смешанном соединении
Важно! Метод эквивалентных преобразований применяется тогда, когда питание рассматриваемого участка цепи осуществляется от одного источника электрического тока, а также при определении Rэкв. в замкнутом контуре с одной ЭДС.
Такой относительный способ определения Rэкв используют и для изучения зависимости токов в некоторой цепи от значения R нагрузки. Это метод эквивалентного генератора, при котором сложный двухполюсник, являющийся активным, представляют эквивалентным генератором. При этом считают, что ЭДС его соответствует Uх.х. (холостого хода) на зажимах, R внутреннее соответствует R входному двухполюсника пассивного на тех же зажимах. Для такого определения источники тока разъединяют, а канал ЭДС закорачивают.
Параллельное соединение
Сопротивление тока: формула
Когда условные выходы деталей имеют общий контакт в одной точке (узле) схемы, а условные входы так же объединены во второй, говорят о параллельном соединении. Узел на чертеже обозначается графической точкой. Это место, где происходят разветвления цепей в схемах. Такой вариант подключения резисторов обеспечивает одинаковое падение напряжения U для всех параллельных элементов. Ток в этой позиции будет равен сумме токов, идущих по каждому компоненту.
Когда в параллельное подключение входит n резистивных элементов, то разность потенциалов, ток и общее сопротивление будут иметь следующие выражения:
- общий ток: I = I1 + I2 + … + In;
- общее напряжение: U = U1 = U2 = … = Un;
- Rобщ. = Rэкв. = U/I1 + U/I2 + …+ U/In) = 1/R1 + 1/R2 +…+ 1/Rn.
Величину, обратно пропорциональную сопротивлению 1/R, называют проводимостью.
Если n равных по номиналу сопротивлений включить параллельно, то Rэкв. = (R*R)/n*R = R/n. Формула подходит и для индуктивных сопротивлений проволочных катушек и ёмкостных сопротивлений конденсаторов.
Параллельное включение резисторов