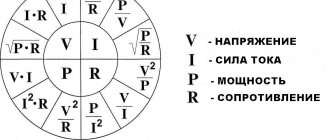
В курсе общей физики для расчета электрических цепей используют, в основном, законы Ома и Кирхгофа, в которые входят напряжения, токи и сопротивления. Однако для расчета сложных электрических цепей, и в особенности цепей переменного тока, целесообразно вместо сопротивления использовать проводимость.
Проводимость в цепи постоянного тока g — величина, обратная сопротивлению
Единицей измерения проводимости в СИ является сименс (в честь немецкого электротехника XIX в. Э. В. Сименса).
1 Сим — это проводимость проводника сопротивлением 1 Ом.
В цепях переменного тока, как известно, существует три типа сопротивлений: активное R, реактивное и полное г. По аналогии с этим введено и три типа проводимостей: активная g, реактивная b и полная у. Однако только полная проводимость у является величиной, обратной полному сопротивлению :
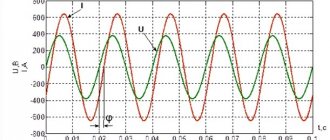
Для введения активной g и реактивной b проводимостей рассмотрим цепь переменного тока из последовательно соединенных активного R и индуктивного сопротивлений (рис. 1-25, а). Построим для нее векторную диаграмму (рис. 1-25, б). Ток в цепи разложим на активную и реактивную составляющие и от полученного треугольника токов перейдем к треугольнику сопротивлений (рис. 1-25, в). Из последнего имеем:
Из векторной диаграммы (см. рис. 1-25, б) с учетом формулы (1.30) имеем:
где активная проводимость,
где реактивная проводимость.
Теперь установим взаимосвязь между проводимостями. Для рассматриваемой цепи имеем:
Подставив значения соответственно из соотношений (1.31) и (1.32), получим:
где полная проводимость цепи.
По аналогии с треугольником сопротивлений (рис. 1-25, в) строим треугольник проводимостей (рис. 1-25, г). По аналогии с индуктивным и емкостным сопротивлениями различают индуктивную и емкостную проводимости.
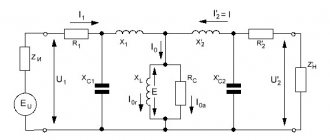
В случае разветвленной цепи (рис. 1-26, а) схему легко преобразовать в так называемую эквивалентную схему (рис. 1-26, б), в которой две ветви заменены одной с соответствующими эквивалентными активным и
реактивным сопротивлениями. Расчет последних сопротивлении, как и других параметров схемы, проще с использованием проводимостей. Установим основные закономерности для проводимостей в разветвленной цепи.
Выразим общий ток через его составляющие или эквивалентные проводимости:
В свою очередь, активная составляющая общего тока равна сумме активных составляющих токов ветвей:
т. е. эквивалентная активная проводимость разветвления равна арифметической сумме активных проводимостей ветвей.
Так как реактивные составляющие ветвей рассматриваемой цепи находятся в противофазе, то для реактивной составляющей общего тока имеем:
т. е. эквивалентная реактивная проводимость разветвления равна алгебраической сумме реактивных проводимостей параллельных ветвей, при этом берется со знаком «плюс», а — со знаком «минус».
. Конденсатор (идеальная емкость)
Аналогичный характер имеют процессы и для идеальной емкости. Здесь . Поэтому из (3) вытекает, что. Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления Х L и Х С, в отличие от активного сопротивления R резистора, – реактивными.
Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью
.
В общем случае выражение для реактивной мощности имеет вид:
Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем токе (емкостная нагрузка-). Единицу мощности в применении к измерению реактивной мощности называютвольт-ампер реактивный
(ВАр).
В частности для катушки индуктивности имеем: , так как.
.
Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора:
.
Резистор (идеальное активное сопротивление).
Здесь напряжение и ток (см. рис. 2) совпадают по фазе , поэтому мощностьвсегда положительна, т.е. резистор потребляет активную мощность
Переходные процессы в линейных электрических цепях. Основные понятия, законы коммуникации.
При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.
Основные методы анализа переходных процессов в линейных цепях:
- Классический метод,
заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
Операторный метод,
заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
Частотный метод,
основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
Метод расчета с помощью интеграла Дюамеля,
используемый при сложной форме кривой возмущающего воздействия.
Метод переменных состояния,
представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
Законы коммутации
| Название закона | Формулировка закона |
| Первый закон коммутации (закон сохранения потокосцепления) | Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: . |
| Второй закон коммутации (закон сохранения заряда) | Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: . |
Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения и, что приводит к нарушению законов Кирхгофа.
На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:
первый закон коммутации –
в ветви с катушкой индуктивности ток в момент
.
второй закон коммутации –
напряжение на конденсаторе в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: .
Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям
(название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).
Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа . Аналогично при размыкании ключа в схеме на рис. 2,б трактование первого закона коммутации как невозможность скачкообразного изменения тока через катушку индуктивности приводит к невыполнению первого закона Кирхгофа. Для данных схем, исходя из сохранения заряда и соответственно потокосцепления, можно записать:
Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для . Необходимое число начальных условий равно числу постоянных интегрирования. Поскольку уравнение вида (2) рационально записывать для переменной, начальное значение которой относится к независимым начальным условиям, задача нахождения начальных условий обычно сводится к нахождению значений этой переменной и ее производных до (n-1) порядка включительно при.
Проводимость
Когда начинающие радиолюбители видят уравнение для расчета общего сопротивления параллельной цепи, у них возникает естественный вопрос , «Откуда оно взялось?». В этой статье мы попытаемся дать ответ на данный вопрос.
Ввиду того что электроны, сталкиваясь с частицами проводника, преодолевают некоторое сопротивление движению, принято говорить, что проводники обладают электрическим сопротивлением
. Сопротивление обозначается буквой «R» и измеряется в Омах. Однако, всякий проводник можно характеризовать не только его сопротивлением, но и так называемой
проводимостью
— способностью проводить электрический ток. Проводимость есть величина, обратная сопротивлению:
Чем больше сопротивление, тем меньше проводимость и наоборот. Сопротивление и проводимость являются противоположными способами обозначения одного и того же электрического свойства материалов. Если при сравнении сопротивлений двух компонентов выясняется, что сопротивление компонента «А» составляет половину от сопротивления компонента «Б», то мы можем альтернативно выразить эту связь, сказав, что проводимость компонента «А» в два раза выше проводимости компонента «Б». Если сопротивление компонента «А» составляет одну треть от сопротивления компонента «Б», то можно сказать, что компонент «А» в три раза проводимее компонента «Б», и так далее.
Обозначается проводимость буквой «G», а ее единицей измерения первоначально было «Мо», то есть «Ом» записанный задом наперед. Но, несмотря на уместность этой единицы, позже она была заменена на «Сименс» (сокращенно — См или S).
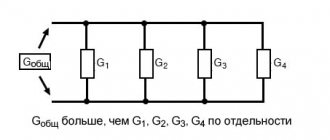
Теперь давайте вернемся к нашему примеру параллельной цепи. Если рассматривать ее с точки зрения сопротивления, то наличие нескольких путей (ветвей) для потока электронов снижает общее сопротивление этой цепи, так как электронам легче течь по нескольким путям, чем по одному, обладающему некоторым сопротивлением. Если рассматривать цепь с точки зрения проводимости, то несколько путей для потока электронов наоборот, увеличивают проводимость схемы.
Общее сопротивление параллельной цепи меньше любого из ее отдельных сопротивлений, поскольку несколько параллельных ветвей создают меньше препятствий потоку электронов, чем каждый резистор по отдельности:
Общая проводимость параллельной цепи больше проводимости любой ее отдельной ветви, поскольку параллельно соединенные резисторы лучше проводят электрический ток, чем каждый резистор по отдельности:
Точнее будет сказать, что общая проводимость параллельной цепи равна сумме ее отдельных проводимостей:
Зная, что проводимость равна 1/R, мы можем преобразовать эту формулу в следующий вид:
Из данной формулы видно, что общее сопротивление параллельной цепи будет равно:
Ну вот мы и нашли ответ на поставленный в начале статьи вопрос! Вам следует знать, что проводимость очень редко используется на практике, в связи с чем данная статья носит чисто образовательный характер.
Краткий обзор:
- Проводимость — это величина противоположная сопротивлению.
- Проводимость обозначается буквой «G» и измеряется в Мо или Сименсах.
- Математически проводимость обратна сопротивлению: G=1/R
Реактивная проводимость обусловлена наличием емкости между фазами и между фазами и землей, так как любую пару проводов можно рассматривать как конденсатор.
Для ВЛЭП величина погонной реактивной проводимости рассчитывается по формулам:
7,58 ×10 — 6 b
0 р lg
D ср
.
R
пр экв
Расщепление увеличивает b
0 на 21¸33%.
Для КЛЭП величина погонной проводимости чаще рассчитывается по фор-
b
0 =
w
×
C
0 .
Величина емкости C
0 приводится в справочной литературе для различных марок кабеля.
Реактивная проводимость участка сети рассчитывается по формуле:
В = b
0 ×
l
.
У воздушных ЛЭП значение b
0 значительно меньше, чем у кабельных ЛЭП,
мало, так как D
ср ВЛЭП >>
D
ср КЛЭП.
Под действием напряжения в проводимостях протекает ёмкостный ток (ток смещения или зарядный ток):
I
c =
В
×
U
ф.
Величина этого тока определяет потери реактивной мощности в реактивной проводимости или зарядную мощность ЛЭП:
DQ c
=
Q
зар = 3 ×
U
×
I c
=
B
×
U
2 .
В районных сетях зарядные токи соизмеримы с рабочими токами. При U
ном = 110 кВ, величина
Q
с составляет около 10% от передаваемой активной мощности,
при U
ном = 220 кВ –
Q
с ≈ 30%
Р
. Поэтому ее нужно учитывать в расчетах. В сети номинальным напряжением до 35 кВ величиной
Q
с можно пренебречь.
Схема замещения ЛЭП
Итак, ЛЭП характеризуется активным сопротивлением R
л, реактивным соп-
ротивлением линии х
л, активной проводимостью
G
л, реактивной проводимостью
В
л.В расчетах ЛЭП может быть представлена симметричными П-и Т-образнымисхемами (рис. 4.6).
| R | X | R/2 X/2 | X/2 |
| R/2 | |||
| B /2 | G /2 | B /2 | |
| G | B | ||
| G/2 |
Рисунок 4.6 – Схемы замещения ЛЭП: а) П – образная; б) Т — образная
П – образная схема применяется чаще.
В зависимости от класса напряжения теми или иными параметрами полной схемы замещения можно пренебречь (см. рис. 4.7):
· ВЛЭП напряжением до 110 кВ (DР
кор » 0);
· ВЛЭП напряжением до 35кВ (DР
кор » 0, D
Q
c » 0);
· КЛЭП напряжением 35кВ (реактивное сопротивление » 0)
· КЛЭП напряжением 20 кВ (реактивное сопротивление » 0, диэлектричес-кие потери » 0);
· КЛЭП напряжением до 10 кВ (реактивное сопротивление » 0, диэлектри-ческие потери » 0, DQ
c » 0).
| Х | R | Х | R | |
| B /2 | B /2 | |||
| а) | б) | |||
| R | ||||
| R | R | |||
| G/2 | B/2 | B/2 | B/2 | B/2 |
| G/2 | ||||
| в) | г) | д) |
Рисунок 4.7 – Упрощенные схемы замещения ЛЭП:
а) ВЛЭП при U
ном до 110 кВ;
б) ВЛЭП при U
ном до 35 кВ; в) КЛЭП при
U
ном 35 кВ;
г) КЛЭП при U
ном 20 кВ; д) КЛЭП при
U
ном 6-10 кВ;
Лекция № 5
Параметры схемы замещения трансформаторов
13. Общие сведения.
14. Двухобмоточный трансформатор.
15. Трехобмоточный трансформатор.
16. Двухобмоточный трансформатор с расщепленной обмоткой низкого напряже-ния.
17. Автотрансформатор.
Общие сведения
На электростанциях и подстанциях устанавливаются трехфазные и однофаз-ные, двухобмоточные и трехобмоточные силовые трансформаторы и автотранс-форматоры, и силовые однофазные и трехфазные трансформаторы с расщеп-ленной обмоткой низшего напряжения.
В аббревиатуре трансформатора последовательно (слева направо) приво-дится следующая информация:
· вид устройства (А
– автотрансформатор, без обозначения – трансфор-матор);
· количество фаз (О
– однофазный,
Т
–трехфазный);
· наличие расщепленной обмотки низшего напряжения – Р
;
· система охлаждения (М
– естественная циркуляция масла и воздуха,
Д
– принудительная циркуляция воздуха и естественная циркуляция масла,
МЦ
–естественная циркуляция воздуха и принудительная циркуляциямасла,
ДЦ
– принудительная циркуляция воздуха и масла и др);
· количество обмоток (без обозначения – двухобмоточный, Т
– трехобмо-точный);
· наличие устройства регулирования напряжения под нагрузкой (РПН);
· исполнение (З
– защитное,
Г
– грозоупорное,
У
– усовершенствованное,
Л
– с литой изоляцией);
· специфическая область применения (С
– для систем собственных нужд электростанций,
Ж
– для электрификации железных дорог);
· номинальная мощность в кВ∙А,
· класс напряжения обмоток (напряжения сети, к которой подключается трансформатор) в кВ.
Двухобмоточный трансформатор
На электрических схемах двухобмоточный трансформатор представляется следующим образом (рис. 5.1):
| В обмотках указывается схемы со- | |
| ВН | единения обмоток (звезда, звезда с ну- |
| лем, треугольник) и режим работы ней- | |
| трали: | |
| · звезда – с изолированной нейт- ра- | |
| НН | лью; |
| · звезда с нулем – имеется соеди- | |
| нение нейтрали с землей. | |
| Рисунок 5.1 – Условное изображение | В соответствии с принятой систе- |
| двухобмоточного | мой обозначений аббревиатура транс- |
| трансформатора. | |
| форматора ТДН-10000/110/10 расшиф- | |
| ровывается: трансформатор трехфаз- |
ный, двухобмоточный с принудительной циркуляцией воздуха и естественной циркуляцией масла и системой регулирования напряжения под нагрузкой. Номи-нальная мощность – 10000 кВ∙А, класс напряжения обмотки высшего напряжения
– 110 кВ, низшего напряжения – 10 кВ.
В практических расчетах двухобмоточный трансформатор чаще всего пред-ставляется Г-образной схемой замещения (рис. 5.2).
| U 1 | R т | X т | U 2 * |
| В т | G т |
Рисунок 5.2 – Г-образная схема замещения двухобмоточного трансформатора
X
т =
X
в +
X
н * .
Активное и реактив-ное сопротивления трас-форматора (продольная ветвь) представляют собой сумму активных и реак-тивных сопротивлений об-мотки высшего напряже-ния и приведенной к ней обмотки низшего напря-жения:
R
т =
R
в +
R
н * ;
Поперечная ветвь схемы замещения представлена активной G
т и реактивной
В
т проводимостями.Проводимости обычно подключают со стороны первичнойобмотки: для повышающих трансформаторов – со стороны обмотки низшего напряжения, для понижающих – со стороны обмотки высшего напряжения.
В такой схеме замещения отсутствует трансформация, то есть отсутствует идеальный трансформатор. Поэтому в расчетах вторичное напряжение U
2 * оказы-вается приведенным к напряжению первичной обмотки.
Активная проводимость обусловлена потерями активной мощности в стали трансформатора на перемагничивание и вихревые токи, реактивная проводимость
– намагничивающей мощностью. В расчетах режимов электрической сети прово-димости заменяются нагрузкой, равной потерям холостого хода.
Параметры схемы замещения трансформатора определяются из двух опытов
– холостого хода и короткого замыкания. В опытах определяют следующие вели-чины, которые указывают в паспортных данных трансформатора:
· потери активной мощности в режиме холостого хода DP
х в кВт;
· потери активной мощности в режиме короткого замыкания DP
к в кВт;
· напряжение короткого замыкания U
к, в %;
· ток холостого хода I
х, в %.
Величины активного и реактивного сопротивлений находят из опыта корот-кого замыкания (рис. 5.3). Опыт выполняют следующим образом: обмотку низше-го напряжения закорачивают, а на обмотку высшего напряжения подают такое напряжение (U
к), чтобы в обеих протекал номинальный ток.
| Так | как | напряжение |
| I 1ном | короткого | замыкания |
| I 2ном | намного | меньше номи- |
| U к | нального | напряжения |
| трансформатора, то поте- | ||
| ри активной мощности в | ||
| проводимости | практиче- | |
| ски равны нулю. Таким | ||
| Рисунок 5.3 – Опыт короткого замыкания | образом, | все потери ак- |
| тивной мощности в режи- | ||
| двухобмоточного трансформатора. | ||
| ме короткого | замыкания | |
| идут на нагрев обмоток. Математически это можно записать: | ||
| DP =3× I 2 | × R . | (5.1) |
| к | 1ном | т |
Если в формуле (5.1) значение тока записать через мощность и номинальное напряжение обмотки высшего напряжения
Напряжение короткого замыкания U
к складывается из падения напряжения на активном
U
к а и реактивном
U
к р сопротивлениях. Выразим их в процентах от номинального напряжения.
Падение напряжения в активном сопротивлении трансформатора:
| U | к а | 3 ×I | ×R | ||
| U | , % = | ×100 = | 1ном | т | ×100. |
| к а | U в ном | U в ном |
Подставим в выражение значение R
т. Получим:
| ×DP × U 2 | |||||||||
| 3 ×I | ×R | 3 ×I | DP | ||||||
| U | , % = | 1ном | т | ×100 | = | 1номк в ном | ×100 = | к | ×100. |
| к а | |||||||||
| U в ном | U в ном × S ном 2 | S ном |
Таким образом, величина падения напряжения в активном сопротивлении, выраженная в процентах, пропорциональна потерям активной мощности в режиме короткого замыкания.
Выражение для падения напряжения в реактивном сопротивлении в процен-тах выглядит следующим образом
| U к р | |||||
| 3 ×I | ×X | т | |||
| U | , % = | ×100 = | 1ном | ×100. | (5.2) |
| к р | U в ном | U в ном |
Из него можем найти величину реактивного сопротивления трансформатора:
| X т = | U кр × U в ном | . |
| × | 3 × I 1 ном |
Умножим и разделим полученное выражение на U
в ном:
| X т = | U кр × U в ном | × | U в ном | = | U кр × U в 2 ном | . |
| U в ном | 100 × S ном | |||||
| × 3 | × I 1 ном |
В современных трансформаторах активное сопротивление гораздо больше реактивного. Поэтому в практических расчетах можно принять, что U
к р ≈
U
к. То-гда, формула для расчета индуктивного сопротивления трансформатора имеет вид:
| X | = | U к × U в 2 | ном | . |
| т | ||||
| × S ном |
Трансформаторы имеют устройства регулирования напряжения (РПН или ПБВ), которые позволяют менять коэффициенты трансформации. Поэтому вели-
чина U
к (следовательно, и величина индуктивного сопротивления) зависит от от-ветвления устройств РПН или ПБВ. В расчетах установившихся режимов этой за-висимостью пренебрегают. Ее учитывают при расчете токов короткого замыкания при выборе устройств автоматики и релейной защиты.
Проводимости ветви намагничивания определяются из опыта холостого хода (рис. 5.4), который выполняется при номинальном напряжении. В этом режиме трансформатор потребляет мощность, равную потерям холостого хода:
I
2 = 0
Рисунок 5.4 – Опыт холостого хода двухобмоточного трансформатора.
| G | = | DP х | . |
| т | |||
| U в 2 | |||
| ном |
DS
х = D
P
х +
j
D
Q
х.
Потери активной мощности пропорцио-нальны активной про-водимости трансфор
DP
х =
U
в 2 ном ×
G
т.
Отсюда может быть определена вели-чина активной прово-
Потери реактивной мощности пропорциональны реактивной проводимости трансформатора:
DQ
х =
U
в 2 ном ×
B
т.
Следовательно, величина реактивной проводимости трансформатора равна:
B
т = D
Q
х.
U
в 2 ном
Величина потерь реактивной мощности пропорциональна току намагничива-
| DQ х =3× I m × U в ном ф, | (5.3) |
где U
ном ф – фазное номинальное напряжение трансформатора.
Величина тока холостого хода складывается из тока намагничивания I
μ и то-ка в стали
I
стали:
I
х=
I
μ+
I
стали.
Так как величина тока в стали составляет около 10 % от тока намагничива-ния, то выражение (5.3) можно записать:
DQ
х »3×
I
х ×
U
в ном ф.
В паспортных данных величина тока холостого хода приводится в процентах от номинального тока. Поэтому мы можем записать:
С учетом полученного выражения, формула для расчета реактивной прово-димости имеет вид:
B
т =
I
х % × ×
S
ном.
На рис. 14.14, а параллельно соединены те же элементы цепи, которые были рассмотрены (см. рис. 14.7, а). Предположим, что для этой цепи известны напряжение u = U m sinωt
. и параметры элементов цепи R, L, С. Требуется найти токи в цепи и мощность.
Активное сопротивление проводов и кабелей
Из электротехники известно, что полное сопротивление при равных условиях переменному и постоянному току будут отличаться. Касается это также проводов и кабелей. Это вызвано тем, что переменный ток распределяется по сечению неравномерно (поверхностный эффект). Однако для проводов из цветных металлов и с частотой переменного напряжения 50 Гц этот эффект не оказывает слишком большого влияния и им можно пренебречь. Таким образом, при расчете проводников из цветных металлов, их сопротивления переменному и постоянному току принимаются равными.
На практике активное сопротивление медных и алюминиевых проводников рассчитывают по формуле:
Где: l – длина в км, γ – удельная проводимость материала провода м/ом∙мм2, r0 – активное сопротивление 1 км провода на фазу Ом/км, s – площадь поперечного сечения, мм2.
Величина r0, как правило, берется из таблиц справочников.
На активное сопротивление провода влияет и температура окружающей среды. Величину r0 при температуре Θ можно определить по формуле:
Где: α – температурный коэффициент сопротивления; r20 – активное сопротивление при температуре 20 0С, γ20 – удельная проводимость при температуре в 20 0С.
Стальные провода обладают значительно большими активными сопротивлениями, чем аналогичные провода из цветных металлов. Его увеличение обусловлено значительно меньшей величиной удельной проводимости и поверхностным эффектом, который у стальных проводов выражен гораздо более ярко, чем у алюминиевых или медных. Более того, в стальных проводах присутствуют потери активной энергии на вихревые токи и перемагничивание, что в схемах замещения линий учитывают дополнительной составляющей активного сопротивления.
Активное сопротивление стальных проводов (в отличии от проводов из цветных металлов) сильно зависит от величины протекаемого тока, поэтому использовать постоянное значение удельной проводимости при расчетах нельзя.
Активное сопротивление стальных проводов в зависимости от протекающего тока аналитически выразить весьма трудно, поэтому для его определения используют специальные таблицы.
Векторная диаграмма для цепи с параллельным соединением ветвей. Метод векторных диаграмм
Для мгновенных величин в соответствии с первым законом Кирхгофа уравнение токов
Представляя ток в каждой ветви суммой активной и реактивной составляющих, получим
Для действующих токов нужно написать векторное уравнение
Численные значения векторов токов определяются произведением напряжения и проводимости соответствующей ветви.
На рис. 14.14, б построена векторная диаграмма, соответствующая этому уравнению. За исходный вектор принят, как обычно при расчете цепей с параллельным
соединением ветвей,вектор
напряжения U,
а затем нанесены векторы тока в каждой ветви, причем направления их относительно вектора напряжения выбраны в соответствии с характером проводимости ветвей. Начальной точкой при построении диаграммы токов выбрана точка, совпадающая с началом вектора напряжения. Из этой точки проведен вектор l 1aактивного тока
ветви
I
(по фазе совпадает c напряжением), а из конца его проведен вектор
I 1p реактивного тока
той же ветви (опережает напряжение на 90°). Эти два вектора являются составляющими вектора
I 1 тока первой ветви
. Далее в том же порядке отложены векторы токов других ветвей. Следует обратить внимание на то, что проводимость
ветви 3-3 активная
, поэтому реактивная составляющая тока в этой ветви равна нулю. В
ветвях 4-4 и 5-5 проводимости реактивные
, поэтому в составе этих токов нет активных составляющих.
Индуктивное сопротивление проводов и кабелей
Для определения индуктивного сопротивления (обозначается Х) кабельной или воздушной линии определенной протяженности в километрах удобно пользоваться выражением:
Где: Х0 – индуктивное сопротивление одного километра провода или кабеля на фазу, Ом/км.
Х одного километра воздушной или кабельной линии можно определить по формуле:
Где: Dср – расстояние среднее между проводами или центрами жил кабелей, мм; d – диаметр токоведущей жилы кабеля или диаметр провода, мм; μт – относительная магнитная проницаемость материала провода;
Первый член правой части уравнения обусловлен внешним магнитным полем и называется внешним индуктивным сопротивлением Х0/. Из этого выражения видно, что Х0/ зависит только от расстояния между проводами и их диаметра, а так как расстояние между проводами выбирается исходя из номинального напряжения линии, соответственно Х0/ будет расти с ростом номинального напряжения линии. Х0/ воздушных линий больше, чем кабельных. Это связано с тем, что токоведущие жилы кабеля располагаются друг к другу значительно ближе, чем провода воздушных линий.
Для одной фазы:
Где: D1:2 расстояние между проводами.
Для одинарной трехфазной линии при расположении проводов по треугольнику:
При горизонтальном или вертикальном расположении проводов трехфазной линии в одной плоскости:
Увеличение сечения проводов линии ведет к незначительному уменьшению Х0/.
Второй член уравнения для определения X0 обусловлен магнитным полем внутри проводника. Он выражает внутреннее индуктивное сопротивление Х0//.
Таким образом выражение для Х0 можно представить в виде:
Для линий из немагнитными материалов μ = 1 внутреннее индуктивное сопротивление Х0// по сравнению с внешним Х0/ составляет ничтожную величину, поэтому им очень часто пренебрегают.
В таком случае формула для определения Х0 примет вид:
Для практических расчетов индуктивные сопротивления кабелей и проводов определяют по соответствующим таблицам.
В случае приближенных расчетов можно считать для воздушных линий напряжением 6-10 кВ Х0 = 0,3 – 0,4 Ом/км, а для кабельных Х0 = 0,08 Ом/км.
Внутренне индуктивное сопротивление стальных проводов сильно отличается от Х0// проводов из цветных металлов. Это вызвано тем, что Х0// пропорционально магнитной проницаемости μr, которая сильно зависит от величины тока в проводе. Если для проводов из цветных металлов μr = 1, то для стальных проводов μr может достигать величины в 103 и даже выше.
Х0// для линий прокладываемых стальными проводами пренебрегать нельзя. Как правило, данную величину берут из таблиц, составленных на основе экспериментальных данных.
Сопротивления r0 и Х0// при некоторых значениях тока могут достигать максимальных значений, а затем с увеличением тока уменьшатся. Это явление объясняется магнитным насыщением стали.
Расчетные формулы для цепи с параллельным соединением ветвей. Метод векторных диаграмм
Из векторной диаграммы
видно, что все активные составляющие векторов тока направлены одинаково — параллельно вектору напряжения, поэтому векторное сложение их можно заменить арифметическими найти активную составляющую общего тока:
I а = I 1a + I 2a + I 3a
.
Реактивные составляющие
векторов токов перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая общего тока в цепи определяется их алгебраической суммой, в которой индуктивные токи считаются положительными, а емкостные — отрицательными:
I p = — I 1p + I 2p — I 4p + I 5p
.
Векторы активного, реактивного и полного тока всей цепи образуют прямоугольный треугольник, из которого следует
Следует обратить внимание на возможные ошибки при определении полной проводимости цепи по известным проводимостям отдельных ветвей:
нельзя
складывать арифметически проводимости ветвей, если токи в них не совпадают по фазе.
Полную проводимость
цепи в общем случае определяют как гипотенузу прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активная и реактивная проводимости всей цепи:
От треугольника токов можно перейти также к треугольнику мощностей и для определения мощности получить известные уже формулы
Активную мощность
цепи можно представить как арифметическую сумму активных мощностей ветвей.
Реактивная мощность
цепи равна алгебраической сумме мощностей ветвей. В этом случае индуктивная мощность берется положительной, а емкостная — отрицательной: