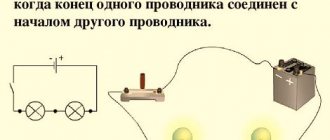
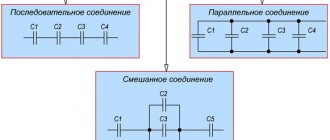
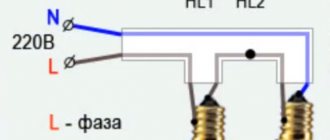
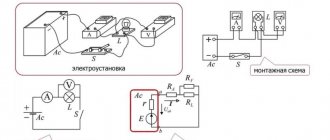
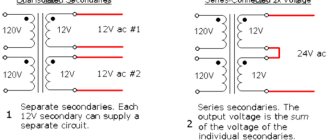
Соединение резисторов — это взаимное расположение данных элементов в цепи относительно друг друга и источника питания. Можно по отдельности выделить последовательное и параллельное соединение резисторов. Когда в схеме присутствуют оба варианта, то такое соединение называется смешанным.
Нам известно, что резистор — это электронный компонент, который обладает электрическим сопротивлением и мощностью рассеивания. Если в цепи имеется несколько резисторов, то для получения общего сопротивления прибегают к расчетам по правилам последовательного или параллельного соединения. Помимо общего сопротивления, группы резисторов по закону Ома влияют на напряжение и силу тока на участках цепи. И в данном обзоре будет доступно рассмотрена методика расчета общего сопротивления при различных видах соединения резисторов. Также будет рассмотрен наглядный пример со смешанным соединением резисторов, где помимо сопротивлений будут просчитаны напряжения и сила тока на разных участках.
Стоит сразу отметить, что в данной теме рассеивающая мощность резисторов вынесена за скобки. Мощность важна при подборе и комбинировании резисторов в схеме, но это уже отдельная тема. К тому же все рассмотренные примеры взяты с учетом источника переменного напряжения 220 В. Почему так? Об этом вы узнаете в последнем пункте публикации.
Последовательное соединение резисторов
Последовательное соединение резисторов — это такое взаимное расположение компонентов, при котором ток движется в одном направлении и имеет общее значение для каждого резистора. При таком соединении напряжение на каждом участке будет пропорционально сопротивлению конкретного резистора в цепи.
Принципиальная схема последовательного соединения:
Как видно в цепи последовательно соединено три резистора (их может быть и больше). Сопротивление первого резистора R1 = 20 Ом. Второго R2 = 70 Ом. Третьего R3 = 10 Ом.
Для подсчета общего (эквивалентного) сопротивление при последовательном соединении нужно сложить все номинальные сопротивления резисторов входящих в цепь:
R = R1 + R2 + R3 + … + Rn.
R = 20 + 70 + 10 = 100 Ом.
В представленной схеме для наглядности приведены напряжения на каждом из трех участков. И падение напряжения происходит в зависимости от сопротивления конкретного резистора. Сила тока в цепи общая для всех резисторов (I = I1 = I2 = I3). Поэтому согласно закону Ома сила тока при известном напряжении источника питания (в данном случае U = 220 В) определяется по формуле:
I = U / R = U / (R1 + R2 + R3 + … + Rn).
I = 220 / (20 + 70 + 10) = 220 / 100 = 2,2 A.
Формулы нахождения напряжения на участке цепи при известной силе тока (в данном случае I = I1 = I2 = I3 = 2,2 A):
- U1 = I × R1.
- U2 = I × R2.
- U3 = I × R3.
- Un = I × Rn.
Соответственно U1 = 2,2 × 20 = 44 В; U2 = 2,2 × 70 = 154 В; U3 = 2,2 × 10 = 22 В. В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи (220 В).
Рассмотренные три резистора в последовательной цепи можно заменить одним с сопротивлением 100 Ом:
Если можно несколько резисторов заменить одним, то возникает логичный вопрос, зачем применяется такое комбинирование. Простыми словами можно ответить, что иногда невозможно подобрать резистор с требуемыми параметрами или необходимо создать более сложные электронные схемы. В этом случае прибегают к последовательному, параллельному или смешанному соединению в цепи.
В цепи из последовательно соединенных резисторов главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление. К примеру, если соединить три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате получиться составной с сопротивлением 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом. А если убрать резистор на 10 Ом, то сопротивление незначительно уменьшиться до 101 Ом.
Виды соединений потребителей.
Различают последовательное, параллельное и смешанное соединение потребителей.
Припоследовательном соединении потребителей конец первого потребителя присоединяется к началу второго, конец второго – к началу третьего и т.д.
Рисунок 9 – Схема последовательного соединения потребителей
1) Сила тока на всех потребителях одинаковая
2)
Общее сопротивление равно сумме сопротивлений отдельных потребителей
3) Напряжение на зажимах цепи равно сумме падений напряжений на отдельных её участках .
При необходимости уменьшить U и I приемника последовательно ему подключают резистор.
Вывод: при выходе из работы одного элемента вся цепь обесточивается, и при изменении сопротивления одного из них меняется ток во всей цепи и напряжение на каждом элементе.
При параллельном соединении элементов цепи все начала собираются в одну точку, а концы в другую точку и включаются в электрическую цепь, образуя параллельные ветви.
Рисунок 10 – Схема параллельного соединения потребителей
1) Общий ток равен сумме токов параллельных ветвей
2) Напряжение на всех потребителях включенных параллельно одинаковое
3) Общее сопротивление будет меньше наименьшего из включенных параллельно
Из закона Ома для участка цепи
—
для двух потребителей
Если сопротивление потребителей равны, то
Вывод:
При выходе из строя одного потребителя остальные остаются включенные в цепь.
Все приемники находятся под одним напряжением независимо от их мощности (сопротивления).
Смешанным называется такое соединение потребителей, когда в цепи имеются одновременно и параллельное и последовательное их соединение.
Цепь постепенно упрощают, заменяя эквивалентным (равноценным) сопротивлением, используя формулы для последовательного и параллельного соединения потребителей.
Дата добавления: 2017-11-21; ;
Похожие статьи:
Параллельное соединение резисторов
Параллельное соединение резисторов — это такое взаимное соединение компонентов, при котором оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов.
При таком соединении напряжение во всей цепи и на каждом участке одинаково и равно напряжению источника питания U = U1 = U2 = U3 = Un. По каждому резистору течет свой ток. Сумма токов всех резисторов дает общую силу тока цепи: I = I1 + I2 + I3 + … + In. Соответственно общая проводимость параллельной цепи равна сумме ее отдельных проводимостей. Проводимость есть величина, обратная сопротивлению, поэтому эквивалентное сопротивление параллельно соединенных резисторов определяется следующим отношением:
1 / R = 1 / R1 + 1 / R2 + 1 / R3 + … + 1 / Rn. Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Рассчитаем общее сопротивление для приведенного выше примера с параллельным соединением резисторов:
1 / R = 1 / 20 + 1 / 70 + 1 / 10 ≈ 0,164.
R ≈ 1 / 0,164 ≈ 6,097 Ом.
Для наглядности смоделируем в программе Electronics Workbench замену трех параллельно соединенных резисторов одним (R = 6,097 Ом):
Как видно, расчет был произведен правильно, так как сила тока в цепи с резистором 6,097 Ом равна силе тока в цепи с параллельным соединением (36,08 A ≈ 36,14 A).
Выделим основные особенности параллельного соединения резисторов:
- Общее сопротивление всегда меньше сопротивления любого параллельно включенного резистора.
- Увеличение числа параллельно соединенных резисторов ведет к уменьшению общего сопротивления и увеличению общей силы тока в цепи.
- Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
- Если в цепи используются резисторы одного номинала, то формула общего сопротивления упрощается и принимает вид R = R1 / N (R1 – номинальное сопротивление резистора; N – количество резисторов с одинаковым номинальным сопротивлением).
Первый закон Кирхгофа
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
Изображение первого закона Кирхгофа.
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Смешанное соединение резисторов
Смешанное соединение резисторов — это комбинация последовательного и параллельного соединения. Иногда такую комбинацию называют последовательно-параллельным соединением.
Пример цепи со смешанным соединением резисторов:
Для расчета эквивалентного сопротивления таких соединений всю цепь разбивают на простейшие участки и придерживаются следующего алгоритма:
| Определяется общее сопротивление участков с параллельным соединением резисторов. | |
| Если эти участки содержат последовательно соединенные резисторы, то сначала вычисляют их общее сопротивление. | |
| После промежуточных расчетов схема перерисовывается, и получается цепь из последовательно соединенных эквивалентных сопротивлений. | |
| Далее рассчитывается сопротивление полученной простой схемы. |
топологические понятия, элементы, схема замещения
2.Законы Ома и Кирхгофа для цепей постоянного тока
3.Последовательное, параллельное и смешанное соединение потребителей
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов. При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I. Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Параллельное соединение резисторов. При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3,
Смешанное соединение резисторов. Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
4.Расчёт цепи постоянного тока методами контурных токов и узловых потенциалов
Метод контурных токов. В основе лежит 2-й закон Кирхгофа. Суть метода в ведении фиктивных контурных токов и их расчёт.
1.Определение числа уравнений: у=в-ви.т-(n-1).
В-число ветвей, ви.т-с источником тока,n-число узлов.
2.Составляем уравнения для неизвестных контурных токов в общем виде.
3.Определяем неизвестные коэффициенты левой и правой части (Е и R).
4.Подставив коэффициенты, решаем уравнения, находим токи контуров.
5.Определяем через контурные токи токи в ветвях.
Метод узловых потенциалов. В основе лежит 1-й закон Кирхгофа. Определяем потенциалы узлов цепи с последующим определением токов в ветвях, используя закон Ома для участков цепи.
1.Подготовка схемы. Обозначим узлы. Потенциал одного из них принимаем за 0.
2.Составляем уравнения потенциалов в общем виде:
Фи1*g11 + фи2*g12 = I11 – для первого узла
Фи1g21 + фи*g22 = I22 – для второго узла
3.Определяем неизвестные проводимости gmn –сумма проводимостей ветвей, подходящих к узлу n.
4.Подставив, решаем уравнения, находим фи1 и фи2.
5.Произвольно выбираем направления токов и, используя закон Ома для участка цепи определяем эти токи: In = (фиX-фиY+En)/Rn.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Ток, протекающий в цепи параллельно соединенных резисторов
Для защиты по току светодиода необходима повышенная корректность при выборе подходящих пассивных элементов питающей цепи. Однако в ряду резисторов представлены только определенные номиналы.
Не решает проблему увеличение бюджета. Прецизионные изделия выпускают с минимальными допусками (0,5% и менее). Но и в этом случае речь идет о точности значений. Номиналы предлагают в соответствии с действующими международными стандартами.
Что делать, если необходимо создать цепь с Rобщ = 11,2 Ом, при наличии серийных резисторов 11 и 12 Ом? Для получения обозначенного результата создают параллельное соединение. Расчет можно сделать с применением онлайн калькулятора на специализированном сайте. Вычисления выполняются автоматически после заполнения простой формы. Такие услуги предлагают бесплатно без регистрации.
Таблица для выбора резисторов
Представленный на рисунке справочный материал поможет подобрать подходящие изделия быстро и точно. Для рассматриваемого примера подойдут резисторы 13 и 82 Ом. При параллельной установке они создадут сопротивление участка цепи 11,2 Ом.
Что такое резистор и для чего он нужен
Резистор — это радиоэлемент, который увеличивает сопротивление цепи. Ставят его обычно для того, чтобы понизить/ограничить напряжение или ток. Есть сопротивления постоянные и переменные.
Например, светодиоды требуют небольшого тока, иначе перегревается и быстро выходит из строя. Чтобы ограничить ток, перед светодиодом поставьте сопротивление. Ток в цепи станет меньше.
Для чего нужны резисторы: для подстройки параметров питания
Постоянные сопротивления — это те, которые не меняют своего номинала в процессе работы. Если это и происходит, то считается выходом из строя.
Так выглядят переменные и постоянные резисторы
Переменные резисторы, наоборот, отличаются тем, что их сопротивление можно изменять. Они имеют бегунок или поворотную ручку, при помощи которых и изменяется номинал. На основе таких устройств делают регуляторы. Например, регулятор громкости, накала греющего элемента и т.д.