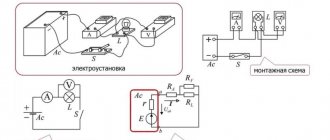
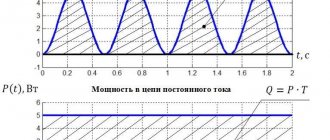
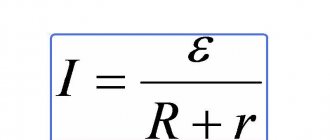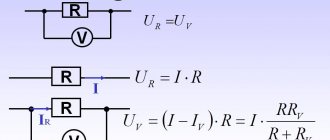Все знают, что действующее напряжение в розетке 220 Вольт (230 по новым нормам, но для данной темы это не имеет особого значения). Это легко проверить при помощи мультиметра, который измерит разность потенциалов между фазой и рабочим нулевым проводником. То есть, при идеальных условиях, потенциал на нулевом проводе 0, а на фазном 220 Вольт. На самом деле все немного не так — переменный ток имеет синусоидальную форму с потенциалом на пиках 310 и -310 Вольт (амплитудное напряжение). Для того чтобы это увидеть, необходимо воспользоваться осциллографом.
Определение
Среднеквадратичное значение (СКЗ) – статическая мера переменной величины. Это полезно, если функция чередует положительные и отрицательные показатели (синусоиды). Перед нами квадратный корень из среднего арифметического квадратов. В случае набора значений n (x1, x2, …., xn) СКЗ определяется по формуле:
Соответствующая формула для непрерывной функции f (t), вычисленной на интервале T1 ≤ t ≤ T2:
Среднеквадратичное значение тока для функции в течение всего времени:
Среднеквадратичное значение напряжения за время периодической функции приравнивается к СКЗ одного периода.
Что такое среднее значение переменного напряжения?
Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением
где Т – период переменного напряжения,
fu(t) – функциональная зависимость напряжения от времени.
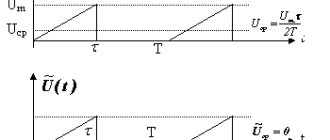
Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией fu(t) и осью Ox за период Т.
Среднее значение переменного напряжения.
В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.
Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно
где Um – максимальное значение напряжения или амплитуда,
ω –угловая частота, скорость изменения аргумента (угла).
Применение к напряжению и току
Давайте взглянем на синусоидально меняющееся напряжение:
(а) – Постоянное напряжение и ток остаются стабильными. (b) – График напряжения и тока в зависимости от времени для мощности переменного тока в 60 Гц. Напряжение и ток выступают синусоидальными и расположены в фазе для простой схемы сопротивления. Частоты и пиковые напряжения сильно отличаются
V = V0sin (2πft), где V – напряжение в момент времени, V0 – пиковое напряжение, f – частота в Гц. Для этой простой схемы сопротивления I = V/R, поэтому ток переменного выглядит как:
I = I0sin (2πft), где I – ток в момент времени, а I0 = V0/R – пиковый ток. Теперь, используя вышеприведенное определение, выведем среднеквадратичные напряжение и ток. Прежде всего, у нас есть
Здесь мы заменили 2πf на ω. Поскольку V0 выступает постоянной, можно разложить ее из квадратного корня и использовать тригонометрическую формулу для замены квадрата синусоидальной функции.
Интегрируя написанное:
Поскольку интервал отображает целое число полных циклов, члены отменяются, оставляя:
Вы также поймете, что СКЗ можно выразить через
Что такое действующее напряжение переменного тока?
Как я писал выше, одним из основных параметров переменного напряжения является амплитуда Um, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному Um ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?
Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения
Для переменного напряжения мгновенное значение выделяемой энергии составит
где u – мгновенное значение напряжения
Тогда количество энергии за полный период от t0 = 0 до t1 = T составит
Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения
Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.
Действующее значение синусоидального напряжения.
Вычислим действующее значение синусоидального напряжения
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.
Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение
Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения
Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.
С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.
Лампочка и постоянное напряжение
Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт
Вот ее характеристики: рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.
Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I — сила тока, можно найти I. Значит I=P/U=21/12=1,75 Ампер.
Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы
Подаем напряжение с блока питания на лампу и вуаля!
Замеряем напряжение на клеммах-крокодилах блока питания с помощью мультиметра . Ровнехонько 12 Вольт, как и предполагалось.
К этим же клеммах цепляем и наш осциллограф
Смотрим осциллограмму:
Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени у нас напряжение остается таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.
Замеряем силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.
Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить на погрешность прибора или на лампочку 
Синусоида действующего и амплитудного напряжения
Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.
И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:
Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.
Начнем со схемы:
- Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
- Резистор 4 Ом — это заземление нейтрали трансформатора.
- Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
- Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.
- К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.
Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.
Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.
Расчёт действующего значения
В качестве примера рассчитаем среднеквадратичное значение синусоидального напряжения.
Запишем выражение U rms
с применением интеграла функции
U = U ampsin(t)
для одного периода 2
π
:
Вынесем U amp
из под знака радикала. Воспользуемся табличным интегралом , перепишем и решим последнее выражение с применением формулы Ньютона-Лейбница:
Так как sin(2π
), sin(4
π
) и sin(0) равны нулю, вычисляем RMS синусоиды следующим образом:
В результате решения в итоге получим:
Расчёт RMS для напряжения или тока треугольной и пилообразной формы можно рассмотреть на примере одного периода T
для функции , представленной на рисунке:
Обновленное уравнение контура
Многие из выведенных уравнений относятся к переменному току. Если нам нужно получить усредненный по времени результат, то соответствующие переменные выражаются в СКЗ. К примеру, закон Ома передается как
Различные выражения для мощности переменного тока выглядят как:
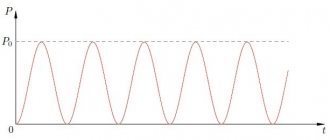
Отсюда видно, что можно вывести среднюю мощность, основываясь на пиковом напряжении и токе.
Мощность переменного тока, основываясь на времени. Напряжение и ток пребывают в фазе, а их продукт колеблется между нулем и IV. Средняя мощность – (1/2) IV
СКЗ полезны, если напряжение меняется по форме сигнала, отличающегося от синусоидов (квадратные, треугольные или пилообразные волны).
Синусоидальные, квадратные, треугольные и пилообразные волны
В зарубежной терминологии применяется аббревиатура RMS (rms) – root mean square. В математике для набора чисел x1, x2, . xn количеством n среднеквадратичное значение (rms) определяется выражением:
Например, для чисел 2,3 и 6 среднеквадратичным значением будет квадратный корень из (2²+3²+6²)/3. √(49/3) = 4.04
Среднеквадратичным значением двух или нескольких чисел является квадратный корень из среднеарифметического значения квадратов этих чисел.
Для любой непрерывной функции в интервале T
1 –
T
2 среднеквадратичное значение можно рассчитать по формуле:
Среднеквадратичное значение применяется в расчётах, где существует пропорциональная зависимость не самих переменных значений, а их квадратов.
Среднеквадратичное значение (RMS) для дискретных данных
Как преобразовать приведенную выше формулу во что-то, что можно применить к дискретным данным? Другими словами, как мы можем вычислить среднеквадратичное значение оцифрованного сигнала?
Давайте посмотрим на это так: сначала, вместо функции (например, x(t)), мы возводим в квадрат отдельные значения (например, x[1], x[2], x[3] и т.д.). Затем, когда мы переходим от сигнала, непрерывного по времени, к сигналу, дискретному времени, интегрирование становится суммированием, а временной интервал становится «интервалом» точек данных, то есть количеством точек данных, которые были суммированы. И в конце у нас идет квадратный корень, который не меняется.
Таким образом, мы можем записать наш расчет среднеквадратичного значения (RMS), дискретного по времени, следующим образом:
\[X_{RMS}=\sqrt{\frac{1}{N}(x[1]^2 + x[2]^2 + … + x[N]^2)}\]
Это начинает казаться знакомым? Мы возводим значения в квадрат, суммируем их, делим на количество значений и извлекаем квадратный корень.
Есть только два отличия между этой процедурой и процедурой, которую мы используем для расчета стандартного отклонения:
- В случае RMS мы делим на N; со стандартным отклонением мы (обычно) делим на N–1. Мы можем игнорировать эту разницу, потому что использование N–1 – это просто попытка компенсировать небольшой размер выборки (для получения дополнительной информации смотрите предыдущую статью).
- В случае RMS мы возводим в квадрат точки данных; в случае стандартного отклонения мы возводим в квадрат разницу между каждой точкой данных и средним значением.
Если мы пытаемся установить связь между среднеквадратичным значением и стандартным отклонением, второе различие может показаться решающим.
Однако учтите следующее: если среднее значение равно нулю, как это часто бывает в электрических сигналах, не будет никакой разницы между вычислением RMS и вычислением стандартного отклонения. Другими словами, для сигнала без смещения по постоянному току стандартное отклонение сигнала также равно среднеквадратичному значению.
Средневыпрямленное значение напряжения
Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая «пробивает пол» берут не с отрицательным знаком, а с положительным.
средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.
На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:
Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:
Методы определения потерь энергии в электрических сетях
Определение потерь энергии методом графического интегрирования
Для определения потерь этим методом необходимо иметь график электрических нагрузок, например, рис. 3.9.
Метод заключается в вычислении площадей участков, на которые разбивается график
Потери энергии от протекания тока нагрузки по элементу электрической сети определяются:
де
n – количество участков, на которые разбивается график:
Метод имеет высокую степень точности, но необходимость графика нагрузок делает его трудоемким и не позволяет использовать метод графического интегрирования в процессе проектирования.
Метод среднеквадратичного тока (среднеквадратичной мощности)
Достоинство этого метода в том, что среднеквадратичный ток (или мощность) вычисляется только один раз для серии расчетов.
Рис.3.10. К определению среднеквадратичного тока
Среднеквадратичный ток Iср.кв – это такой условный неизменный по величине ток, при протекании которого по сети в течение расчетного периода выделяются те же потери энергии, что и при протекании действительного тока, изменяющегося по графику нагрузки
Это проиллюстрировано на рис. 3.10, где площадь фигуры «оабсден» пропорциональна потерям энергии (3.32) и равна по площади фигуре «оmkн», т.е. квадрат среднеквадратичного тока I2ср.кв позволяет найти потери энергии:
Среднеквадратичный ток можно определить:
Переходя от тока к мощности, определим среднеквадратичную мощность за год:
:
Sср.кв = Sнб(0,12 + Tнб 10-4),
где Тнб, час — время использования наибольшей нагрузки – это время, течение которого при передаче по сети наибольшей нагрузки будет передана та же энергия W = РнбТнб, что и при реальном графике (рис.3.11).
Tнб – важнейший показатель, который характеризует как потребителя, так и электрическую сеть в целом (рис.3.7). Так для односменных предприятий Тнб=2000-3000ч; для двухсменных — Тнб=3000-4500ч; для трехсменных — Тнб=4500-8000ч; для коммунально-бытовой нагрузки Тнб=1300-3500ч.
Потери электроэнергии находятся по формуле, эквивалентной (3.38):
3.8.3. Метод времени наибольших потерь
Временем наибольших потерь t называется время, за которое при передаче наибольшей нагрузки в сети возникнут те же потери электроэнергии, что и при работе сети по действительному графику нагрузки.
t = (0,124 + Тнб 10-4)2 8760, час.
Потери энергии в линиях и трансформаторах
Определение потерь энергии методом графического интегрирования в линии может быть произведено путем суммирования значений потерь мощности за бесконечно малые промежутки времени (3.38):
Аналогично находятся потери в трансформаторах:
При использовании метода среднеквадратичного тока потери в линиях и трансформаторах находятся по следующим формулам:
Работа генератора трехфазного переменного тока
Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:
Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.