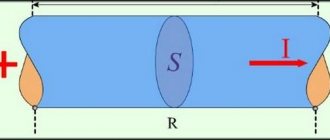
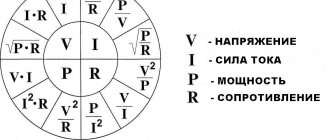
Что такое мгновенное амплитудное и действующее значение переменного тока?

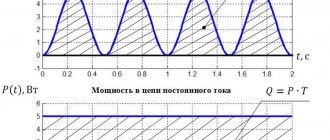
Как найти амплитудное значение напряжения переменного тока?

В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт . Максимальное, амплитудное значение напряжения в сети равно: Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.

Интересные материалы:

Как правильно выключить PSP? Как правильно вынести дисциплинарное взыскание? Как правильно выплачивается аванс и зарплата? Как правильно выращивать имбирь? Как правильно вырастить фикус из отростка? Как правильно вырастить каштан из ореха? Как правильно взять отросток у фикуса? Как правильно закрепить поликарбонат на теплице? Как правильно закрыть фирму? Как правильно закрыть розы?

Ответ

Проверено экспертом

Речь идём о переменном токе.

Мгновенное значение (ЭДС или напряжения или тока) — значение величины в данный момент времени. обозначается чаще всего маленькими буквами: e, u,i.

Амплитудное значение (ЭДС или напряжения или тока) — максимальное значение. Обозначается :

Действующее значение отличается от максимального тем, что оно меньше максимального в раз, т.е.( на примере тока, для напряжения и ЭДС аналогично):

Обозначается действующее значение или без иднекса или с индексом «д»:

(только русское «д»).

Смысл действующего значения: при переменном токе (i) за период выделиться столько же тепла, сколько выделиться при действующем значении

Имеено действующее значение показывают приборы, подключённые в цепь с переменным током.

Среднее значение величин (-//-) -среднее арифметическое значение величины за полпериода.

Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.

Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Закон Ома для типовых соединений

Резисторы, индуктивные катушки, конденсаторы соединяют несколькими способами:

все три элемента последовательно;
все три – параллельно;
два – параллельно, третий – последовательно с ними.

Запись закона Ома не изменяется, только есть отличие – в формуле для общего сопротивления.

Для цепей с активными, реактивными элементами оно называется полным или комплексным, его обозначают символом Z.

Поскольку на конденсаторе, катушке происходит сдвиг фаз, рассматривают не сами сопротивления, а их квадраты.

Катушка имеет активное сопротивление как проводник, индуктивное – как проявление электромагнитной индукции.

Цепь из резистора, катушки обозначают RL. В случае последовательного соединения полное сопротивление:

Z = √(R2 + RL2) = √(R2 + (ωL)2);

Зависимость I для этого случая:

I = U/Z = U/√(R2 + ω2L2);

Участок с резистором и конденсатором – цепь RC. Для соединения последовательно:

Z = √(R2 + RC2) = √(R2 + (1/ωC)2);

Зависимость величин для этого соединения:

I = U/Z = U/√(R2 + (1/ωC)2)

Для соединения последовательно всех элементов (цепь RLC) значение полного сопротивления:

Z = √(R2 + (RL – RC)2) = √(R2 + (ω2L2 – (1/ω2C2)2)).

Комплексное сопротивление параллельного соединения находят из выражения:

1/Z2 = 1/R2 + 1/(RL2 – RC2).

Знание особенностей протекания переменного сигнала в цепи с конденсатором, индуктивной катушкой помогает в расчете радиотехнических цепей. Реактивные элементы используют в фильтрах верхних, нижних частот. Явление возникновения колебаний, резонанса широко применяют в современных средствах связи.

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное

) с угловой частотой, равной
w
. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС
е1
и
е2
(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют
векторными диаграммами.
При построении векторных диаграмм векторы удобно располагать для начального момента времени
(t=0),
что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью
w
. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Закон Ома для катушки индуктивности

Индукционное магнитное поле тормозит движение по проводнику свободных зарядов. Это причина дополнительного (индукционного) сопротивления. Оно зависит от индуктивности L, частоты сигнала:

RL = ωL,

где RL – индуктивное сопротивление.

Зависимость характеристик для участка цепи с катушкой индуктивности приобретает вид:

I = U/RL.

Катушка индуктивности имеет особенность: в ней колебания напряжения и скорости изменения заряда отличаются по фазе.

Колебания напряжения опережают колебания тока на четверть периода:

u = Umsinωt, i = Imsin(ωt – π/2).

Разность между значениями функции sin для 2 колебаний называют сдвигом фаз. Для индуктивной катушки:

ωt – (ωt – π/2) = π/2 = 90°.

Для наглядности сдвиг фаз Δφ изображают в виде векторной диаграммы. Участок цепи, в котором возникает разность фаз между колебаниями тока, напряжения называют реактивной нагрузкой.

ЭДС самоиндукции

При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.

В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:

Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.

Закон Ома для участка цепи с конденсатором

Для неизменного сигнала конденсатор представляет непреодолимое препятствие. Переменный сигнал проходит через него с некоторым усилием. Называют его емкостным сопротивлением.

Оно зависит от электроемкости конденсатора, частоты сигнала и обратно пропорционально произведению:

RC = 1/ωC.

Обозначения:

RC – емкостное сопротивление;
ω – круговая частота;
C – емкость конденсатора.

Зависимость величин для участка цепи с конденсатором записывают так:

I = U/RC.

Конденсатор – реактивная нагрузка. Колебания напряжения, скорости изменения заряда не синхронны. Изменение U отстает от колебаний I на четверть периода:

u = Umsinωt, i = Imsin(ωt + π/2).

Сдвиг фаз составляет 90°. Индуктивные, емкостные нагрузки сдвигают фазу в противоположных направлениях.

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими,

а наименьший промежуток времени, через который эти повторения наблюдаются, —
периодом Т.
Для периодического тока имеем

(1)

Величина, обратная периоду, есть частота,

измеряемая в герцах (Гц):

(2)

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f
= 50Гц
.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

— мгновенное значение тока ;

– мгновенное значение напряжения ;

— мгновенное значение ЭДС ;

— мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m

— амплитуда тока;

— амплитуда напряжения;

— амплитуда ЭДС.

Действующее значение переменного тока

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением

периодического тока:

(3)

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1

и
е2
соответствуют уравнения:

Значения аргументов синусоидальных функций и называются
фазами
синусоид, а значение фазы в начальный момент времени
(t=0):
и —
начальной фазой
().

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой.

Так как фазовый угол синусоиды за время одного периода
Т
изменяется на рад., то угловая частота есть , где
f–
частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз

Для синусоидальных ЭДС е1

и
е2
угол сдвига фаз:

Векторное изображение синусоидально
изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

и .

Результирующий ток также будет синусоидален:

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.

На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для
t=0.
При вращении этих векторов с одинаковой угловой скоростью
w
их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Представление синусоидальных ЭДС, напряжений и токов комплексными числами

Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

показательной

тригонометрической

или

алгебраической

—
формах.
Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число

Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

(4)

Комплексное число удобно представить в виде произведения двух комплексных чисел:

(5)

Параметр , соответствующий положению вектора для t=0

(или на вращающейся со скоростью
w
комплексной плоскости), называют
комплексной амплитудой:
, а параметр —
комплексом мгновенного значения.
Параметр является оператором поворота

вектора на угол
wt
относительно начального положения вектора.

Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ±a

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j”

произведения комплекса амплитуды и оператора поворота :

Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:

(6)

Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

— то для записи ее в показательной форме, необходимо найти начальную фазу , т.е. угол, который образует вектор с положительной полуосью +1:

Тогда мгновенное значение напряжения:

где .

При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)

(7)

а при (третий квадрант)

(8)

или

(9)

Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:

Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.

Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:

где ;

Действующее значение синусоидальных ЭДС, напряжений и токов

В соответствии с выражением (3) для действующего значения синусоидального тока запишем:

Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:

(10)

Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения

Литература

1. Основы

теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2. Бессонов Л.А.

Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?

2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?

3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?

4. Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.

5. На рис. 5 , а . Определить .

Ответ: .

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1

и
е2
соответствуют уравнения:
.

Значения аргументов синусоидальных функций иназываютсяфазами
синусоид, а значение фазы в начальный момент времени
(t=0):
и —
начальной фазой
().

Величину

, характеризующую скорость изменения фазового угла, называют
угловой частотой.
Так как фазовый угол синусоиды за время одного периода
Т
изменяется на рад., то угловая частота есть, где
f–
частота.

.
.

Определение электромагнитной индукции

Возникновение электрического тока в проводнике, движущемся в магнитном поле, называют явлением индукцией в движущихся проводниках. В случае движения проводника в магнитном поле, его свободные электроны приходят в движение относительно проводника под воздействием силы Лоренца. Явление электромагнитной индукции обнаружил Фарадей в 1831 г. в проводящем контуре. Он заметил, что в замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, которую ограничивает контур, появляется электрический ток. Это также явление электромагнитной индукции, возникающий ток в контуре, называют индукционным.
Итак, явление электромагнитной индукции состоит в возникновении электрического тока в замкнутом проводнике при изменении потока магнитной индукции, охватываемого контуром. При этом контур может быть неподвижным.

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы