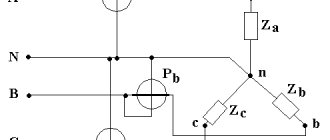
Схема соединения фаз электроприемников «звезда» получила очень широкое распространение в электроэнергетике. Принципиальная схема соединения звездой показана ниже:
Из схемы видно, что фазные напряжения приемника Ua, Ub, Uc не равны линейным напряжениям Uab, Ubc, Uca. Если применить к контурам aNba, bNcb, cNac второй закон Кирхгофа получим соотношение для фазных и линейных напряжений:
Если сопротивления нейтрального провода и линейных проводов не учитывать, то можно предположить, что напряжение на клеммах генератора и электроприемника равны. Вследствие указанного равенства векторные диаграммы для источника и приемника электрической энергии будут одинаковы.
Фазные и линейные напряжения приемника, как и источника, будут образовывать две симметричные системы напряжений. Соответственно между фазными и линейными значениями напряжений будет существовать определенная зависимость:
Далее будет показано, что соотношение (2) будет справедливо лишь при определенных условиях, а также в случае отсутствия нулевого провода, то есть в трехпроводной сети.
Исходя из указанного выше соотношения (2) можно сделать вывод, что соединение звездой лучше применять в случае, когда каждая фаза трехфазного электроприемника или однофазные приемники рассчитаны на напряжение в раз меньше, чем номинальное линейное напряжение сети.
Также из схемы соединения звезда (смотри схему выше) видно, что при соединении приемников звездой фазные токи будут равны линейным:
Применив первый закон Кирхгофа можно получить соотношение между токами при соединении электроприемников звездой:
Зная фазные токи с помощью формулы (4) можно вычислить ток нейтрального провода IN. В случае отсутствия нейтрального провода справедливо будет выражение:
Соединение в звезду трехфазного генератора
Расположим на чертеже изображения трех обмоток ax, by и cz трехфазного генератора под углами 120° так, как это сделано на рисунке 1, а. Присоединим к каждой обмотке нагрузку. В данном случае это сопротивления za, zb и zc. На практике нагрузкой могут быть лампы, печи, электродвигатели и другие электроприемники. Для соединения обмоток генератора с нагрузками потребовалось шесть проводов. В каждый момент времени три из них являются прямыми – ток по ним идет от генератора к нагрузке. Другие три провода – обратные.
Векторы Ea, Eb и Ec расположены параллельно обмоткам и изображают их электродвижущие силы (э. д. с.). Напряжения Ua, Ub и Uc меньше соответствующих э. д. с. на величину падения напряжения в обмотках. Направления токов Ia, Ib и Ic изображены стрелками.
Объединение трех обратных проводов в один дает четырехпроводную схему (рисунок 1, б). В ней провода, присоединенные к выводам генератора а, b и с, называются линейными (или просто фазами). Общий провод называют либо нейтральным на том основании, что он в равной степени принадлежит любой фазе, либо нулевым, так как в ряде случаев ток в нем I0 равен нулю.
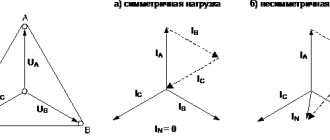
Естественно, возникает вопрос: может ли равняться нулю ток в проводе, по которому в генератор должны возвращаться токи трех фаз? Ответ дает рисунок 1, в, где векторами изображены токи Ia, Ib и Ic (сумма которых образует ток I0) и произведено их сложение. Сначала сложены токи двух фаз, затем их сумма сложена с током третьей фазы. В итоге получен нуль, так как геометрическая сумма токов двух фаз, что отчетливо видно на рисунке 1, в, по величине равна току третьей фазы b и направлена прямо противоположно.
Рисунок 1. Соединение в звезду трехфазного генератора.
Физический смысл полученного результата состоит в том, что благодаря сдвигу фаз между токами в каждый момент времени токи в одних линейных проводах идут от генератора, в других – к генератору. Иными словами, одни из них являются прямыми, другие – обратными. Роль линейных проводов в качестве прямых и обратных, понятно, непрерывно меняется, но так или иначе при равномерной (одинаковой) нагрузке фаз на долю нулевого провода тока не остается.
При равномерной нагрузке фаз нулевого провода не делают, получая, таким образом, трехпроводную схему (рисунок 1, г).
При неравномерной нагрузке в четырехпроводной схеме по нулевому проводу идет только небаланс токов. Поэтому сечение нулевого провода не больше сечения линейных проводов, а, как правило, вдвое меньше. Подробнее вопрос о сечении нулевого провода рассмотрен ниже.
Независимо от того, выполнена схема с шестью, четырьмя или тремя проводами (что для практики, конечно, не безразлично, во-первых, потому что трехпроводные схемы дешевле и, во-вторых, потому что каждая схема обладает определенными свойствами и предназначена для определенных условий), система не перестает быть трехфазной.
Электродвижущие силы Ea, Eb и Ec, напряжения Ua, Ub и Uc и токи Ia, Ib и Ic каждой фазной обмотки называют фазными. Напряжения Uab, Ubc и Uca, действующие между линейными проводами, а также токи в линейных проводах Ia, Ib и Ic называют линейными.
Основные соотношения: 1. При соединении в звезду линейные и фазные токи одинаковы, потому что для тока, проходящего через фазную обмотку, нет иного пути, кроме линейного провода. 2. Линейные напряжения больше фазных √3 = 1,73 раза, откуда вытекают известные соотношения 127 / 220 В (127 х 1,73 = 220); 220 / 380 В (220 х 1,73 = 380), 6,6 / 11 кВ (6,6 х 1,73 = 11) и так далее.
Как доказать, что линейные напряжения √3 = 1,73 раза больше фазных? Для этого придется начать с простого, но хорошо понятного примера. Две батареи с э. д. с. E1 = 5 В и E2 = 7 В можно соединить либо как на рисунке 2, а, либо как на рисунке 2, б. В первом случае соединены разноименные выводы: плюс (начало) одной батареи с минусом (концом) другой, и э. д. с, действующая между свободными разноименными выводами, равна сумме E1 + E2 = 5 + 7 = 12 В. Во втором – соединены одноименные выводы: плюс одной батареи с плюсом другой, и э. д. с, действующая между свободными одноименными выводами, равна разности E1 – Е2 = 5 – 7 = –2 В. Знак минус указывает на изменение направления напряжения на обратное по сравнению с тем, которое было только от одной э. д. с. E1. Короче говоря, результирующая э. д. с. при соединении разноименных выводов равна сумме, а при соединении одноименных выводов – разности составляющих э. д. с. и направлена в сторону большей э. д. с.
Рисунок 2. Определение линейных напряжений при соединении в звезду.
Теперь можно возвратиться к соединению в звезду. Так как в этом случае соединяют одноименные выводы (либо начала, либо концы), то результирующее линейное напряжение находится вычитанием. Сообразуясь со схемой на рисунке 2, в, на которой указано направление вращения фаз и обозначены разности Ua – Ub, Ub – Uс и Uс – Uа (вычитание ведут всегда в одном и том же направлении, то есть из напряжения опережающей фазы вычитают напряжение следующей за ней), на рисунке 2, д выполнено вычитание. Непосредственно измеряя длины векторов либо пользуясь формулами геометрии, легко убедиться, что линейные напряжения (Ua – Ub, Ub – Uc, Uc – Ua) в √3 = 1,73 раза больше фазных Ua, Ub, Uc.
К решению этого же вопроса, то есть к доказательству того, что линейные напряжения определяются вычитанием, можно подойти и иначе. Действительно, если включить лампу так, как показано на рисунке 2, г, то нетрудно видеть, что в лампе токи, созданные действием фазных напряжений Ua и Ub, направлены навстречу. Значит, линейное напряжение Uab надо находить вычитанием, но, понятно, геометрическим.
Из рисунка 2, д отчетливо видно, что векторная диаграмма симметричных линейных напряжений (Ua – Ub, Ub – Uc и Uc – Ua) сдвинута на 30° в сторону вращения векторов относительно диаграммы фазных напряжений Ua, Ub и Uc. Иными словами, напряжение Ua – Ub опережает на 30° Ua, Ub – Uc опережает на 30° Ub и Uc – Ua опережает на 30° Uc.
Сделаем еще один шаг. Перенесем с рисунка 2, д векторы Ua – Ub, Ub – Uc и Uc – Ua параллельно самим себе, так, чтобы их концы и начала оказались у концов векторов Ua, Ub и Uc, образующих звезду. При этом получится треугольник (рисунок 2, е). Из него непосредственно следует, что:
для определения величин линейных напряжений достаточно около звезды фазных напряжений построить треугольник; для определения направлений линейных напряжений у векторов, образующих стороны треугольника, нужно расставить стрелки в направлении вращения фаз.
Симметричная нагрузка при соединении приемников звездой
Нагрузка считается симметричной тогда, когда реактивные и активные сопротивления каждой фазы будут равны, то есть выполняется равенство:
Условие симметричности также может быть выражено через комплексные сопротивления Za = Zb = Zc.
Симметричная нагрузка в сети возникает при подключении трехфазных электроприемников. Будем считать, что данная система имеет нейтральный провод.
В отношении любой из фаз при симметричной нагрузке будут справедливы все формулы, полученные для однофазной сети, например для фазы А:
Так как в четырехпроводной цепи Ua = Ub = Uc = Uл / , то при симметричной нагрузке:
Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена выше. Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе будет равен IN = Ia + Ib + Ic = 0.
Отсюда можно сделать вывод, что при симметричной нагрузке отключение нейтрального провода не приведет к серьезным нарушениям работы электроприемников, то есть не произойдет изменение фазных напряжений, углов сдвига, токов, мощностей.
Из сказанного выше следует, что при симметричной нагрузке в нейтральном проводе нет необходимости, и довольно часто в симметричных системах нейтральный провод не применяется.
Мощность трехфазного приемника электрической энергии при симметричной нагрузке можно выразить формулами:
Как правило, для трехфазных приемников электрической энергии в качестве номинальных параметров указываются линейные напряжения и токи. Исходя из этого, целесообразней выражать мощность трехфазной цепи тоже через линейные напряжения и тока, поэтому подставим в формулу (6) линейные значения и получим:
Пример
К трехфазной электрической цепи с линейным напряжением Uл = Uab = Ubc = Uca = 380 В необходимо подключить трехфазный электроприемник, каждая фаза которого рассчитывается на фазное напряжение в 220 В и имеет активное сопротивление rф = 10 Ом и индуктивное сопротивление хф = 10 Ом, которые соединены последовательно. Необходимо определить мощности, углы сдвига между токами и напряжениями (cos φ) и фазные токи.
Решение
Каждая фаза потребителя электрической энергии рассчитана на напряжение в раз меньше номинального, то фазы потребителя нужно соединять в звезду. Поскольку нагрузка в данном случае симметричная, то нулевой провод (нейтраль) к потребителю можно не подводить.
Фазные тока, углы сдвига cos φ, а также полны сопротивления фаз будут иметь вид:
Активная, реактивная и полная мощности приемника, а также любой фазы будут равны:
Векторная диаграмма для данной системы приводилась выше.
Обозначение линейных напряжений
На рисунке 2, е линейные напряжения обозначены не только как разность соответствующих фазных напряжений, но также и одной буквой с двумя индексами, в нашем примере Uab (Ubc и Uca). Порядок индексов непроизволен: он показывает, в каком направлении производилось вычитание.
Итак, мы из одного фазного напряжения вычли равное ему по величине, но получили не нуль, а величину, в 1,73 раза большую. Этот результат не является неожиданным, так как производилось не алгебраическое, а геометрическое вычитание.
Воспользуемся случаем, чтобы подчеркнуть еще одно важное обстоятельство, с которым в дальнейшем мы неоднократно столкнемся. Оно состоит в том, что при геометрическом вычитании одной величины из другой, равной ей по модулю1 в отличие от алгебраического вычитания можно получить не только нуль, но и любую величину в пределах от нуля до удвоенного значения. Сказанное здесь иллюстрируется на рисунке 3 несколькими примерами. Слева произведено вычитание векторов, совпадающих по фазе (сдвиг 0°), и, естественно, получен нуль. Правее вычитаются векторы, сдвинутые на 45°: разность равна 0,707 длины любого из них и так далее. И, наконец, на рисунке 3 справа – разность оказалась вдвое больше уменьшаемого.
Рисунок 3. Разность векторов зависит от величины угла между ними.
Соединение в звезду электроприемников
Электроприемники могут представлять либо сосредоточенную, либо рассредоточенную нагрузку. Кроме того, она может быть равномерной, как, например, обмотки трехфазных электродвигателей, так и неравномерной, как, например, освещение домов, улиц и тому подобного.
Сосредоточенной нагрузкой являются: электродвигатель (рисунок 4, а), конденсаторная батарея (рисунок 4, б), театральная люстра (рисунок 4, в), где все три фазы расположены в непосредственной близости.
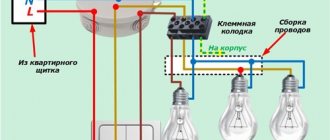
Распределенной нагрузкой являются: осветительные сети домов (рисунки 4, г и д), где от вводного ящика 1 по лестничным клеткам расходятся стояки 2, а от них в свою очередь сделаны ответвления 3 в квартиры. Очень важно понять, что в осветительных сетях не на всех участках существует трехфазная нагрузка.
Действительно, до вводного ящика идут четыре питающих провода: А, В, С и 0. Это настоящая трехфазная сеть – в ней по нулевому проводу проходит только ток небаланса всего дома, определяющийся неравномерностью нагрузки фаз. Это же относится к стоякам 2 на рисунке 4, г, где по нулевому проводу проходит ток небаланса в пределах данной лестничной клетки.
Что же касается стояков на рисунке 4, д, в каждом из которых только одна фаза и нуль, а также ответвлений в квартиры, то они хоть и питаются от трехфазной сети, но представляют собой однофазную нагрузку, так как и по фазному и по нулевому проводам проходит один и тот же ток (других путей нет). Поэтому сечения фазного и нулевого проводов должны быть одинаковы.
Рисунок 4. Соединение в звезду электроприемников.
Заметьте: при равномерной нагрузке (рисунок 4, а – в) применена трехпроводная схема. При неравномерной нагрузке (рисунки 4, г и д) – четырехпроводная.
Чтобы понять, почему делают именно так, обратимся к рисунку 5. На рисунке 5, а показаны три группы одинаковых ламп (то есть имеющих равные номинальные напряжения, в нашем примере 127 В, и равные мощности). При этих условиях и линейном напряжении сети 220 В лампы горят нормальным накалом. Но количество одновременно включенных ламп, а также их мощность в сетях освещения зависят от желания потребителей. В частном случае нагрузка одной из фаз, например фазы с, может быть на некоторое время совсем отключена (рисунок 5, б). И тогда нагрузки двух других фаз окажутся соединенными последовательно. Если они равны, то линейное напряжение разделится между ними поровну и лампы будут гореть с недокалом, так как 220 В / 2 = 110 В – меньше номинального напряжения 127 В.
Значительно хуже, если часть ламп, присоединенных к одной из фаз, например к фазе b, будет отключена, например так, как показано на рисунке 5, в. Действительно, сопротивление одной лампы в 3 раза больше сопротивления группы из трех таких же ламп, соединенных параллельно. Значит, напряжение 220 В разделится между ними неравномерно: на большее сопротивление придется 165 В (¾ от 220 В) и лампа может перегореть; на меньшее сопротивление придется 55 В (¼ от 220 В) 2.
При четырехпроводной схеме (рисунок 5, г) неравномерность нагрузки фаз не сказывается столь сильно на накале ламп благодаря тому, что нагрузка каждой фазы непосредственно присоединена к обоим выводам фазной обмотки генератора или вторичной обмотки трансформатора.
Следует, однако, отметить, что неравномерность нагрузки фаз даже и при наличии нулевого провода – явление нежелательное, особенно в тех случаях, когда нагрузка питается от вторичной обмотки трансформатора, соединенной в звезду, так как при неравномерной нагрузке в трансформаторе нарушается его магнитное равновесие. Этот важный вопрос рассмотрен в статье «Понятие о магнитном равновесии трансформатора».
Рисунок 5. Особенности соединений в звезду осветительной нагрузки.
Несимметричная нагрузка при соединении приемников звездой
Нагрузка трехфазной электрической сети будет считаться несимметричной, если хотя бы одно из фазных сопротивлений не равно другим. Проще говоря, сопротивления фаз не равны, например: ra = rb = rc, xa = xb ≠ xc. В общем случае считают, что несимметричная нагрузка возникает при отключении одной из фаз.
Возникает не симметрия чаще всего при подключении к трехфазной сети однофазных электроприемников. Они могут иметь различные мощности, режимы работы, различное территориальное расположение, что тоже влияет на величину фазной нагрузки.
В случае, когда необходимо подключить однофазные потребители электрической энергии, для более равномерной загрузки их делят на три примерно одинаковые по мощности группы.
Один вывод однофазных потребителей подключают к одной из трех фаз, а второй вывод подключают к нейтральному проводу. Так как все электроприемники рассчитываются на одно напряжение, то в пределах каждой фазы они соединяются параллельно.
Главной особенностью электрической сети несимметричной нагрузкой является то, что она должна в обязательном порядке иметь нейтральный провод. Это объяснимо тем, что при его отсутствии величины фазных напряжений будут в значительной степени зависеть от величины не симметрии сети, то есть от величин и характера сопротивления каждой из фаз. Поскольку сопротивления фаз могут варьироваться довольно в широких пределах в зависимости от количества подключенных электроприемников, также широко будет варьироваться и напряжения на потребителях электрической энергии, а это недопустимо.
Для иллюстрации выше сказанного ниже приведена векторная диаграмма для трехфазной несимметричной цепи при наличии нейтрального провода:
Ниже приведена приведена векторная диаграмма для этой же цепи, но при отсутствии нулевого рабочего (нейтрального) провода:
Также можно посмотреть видео, где объясняется, что может произойти в электрической цепи при обрыве нулевого провода:
Необходимость нулевого провода станет еще более очевидной, если представить, что вам необходимо подключить однофазного потребителя к одной из фаз, при этом остальные две подключать нельзя, так как приемник рассчитан на фазное напряжение 220 В, а не на линейное 380В, как в таком случае получить замкнутый контур для протекания электрического тока? Только использовать нулевой рабочий проводник.
Для повышения надежности соединения электроприемников в цепь нулевого рабочего проводника не устанавливают коммутационную аппаратуру (автоматические выключатели, предохранители или разъединители).
Фазные токи, углы сдвига, а также фазные мощности при несимметричной нагрузке будут различными. Для вычисления их фазных значений можно применить формулу (5), а вот для вычисления трехфазной мощности формула (6) уже не подходит. Для определения мощностей необходимо пользоваться выражением:
Если существует необходимость определения тока нейтрального провода, то необходимо решать задачу комплексным методом. Если существует векторная диаграмма, то определить ток можно по ней.
Пример
В осветительной электрической сети с напряжением в 220 В в фазе А включено 20 ламп, фазе В – 10 ламп, а в фазе С – 5 ламп. Параметры лампы Uном = 127 В, Рном = 100 Вт. Необходимо определить ток нейтрального провода и каждой лампы.
Распределение нагрузки между фазами
Итак, мы всегда стремимся равномерно нагрузить фазы, то есть присоединить к каждой из них одинаковую мощность. При освещении лампами накаливания для этого достаточно правильно распределить лампы между фазами. При люминесцентном освещении надо выполнить еще одно условие, а именно: присоединить лампы, расположенные рядом, к разным фазам. Это объясняется следующим образом: люминесцентные лампы 100 раз в секунду зажигаются и гаснут, так как переменный ток частотой 50 Гц 100 раз в секунду проходит через нуль. Хотя мы не замечаем этих пульсаций света, но они вредно действуют на зрение. Если же рядом расположены лампы, присоединенные к разным фазам, то они будут гаснуть и загораться неодновременно, что значительно снизит глубину изменения светового потока.
Кроме того, глубокое изменение светового потока может исказить действительную картину движения предметов. Пусть, например, вращающийся предмет за время погасания лампы успеет сделать полное число оборотов. Значит, при каждом очередном освещении предмет будет виден в одном и том же положении, то есть будет казаться неподвижным. Если вращающийся предмет успеет за время погасания сделать немного меньше полного оборота, то будет казаться, что вращение происходит в обратную сторону. В производственных условиях, где имеются механизмы с вращающимися деталями, это крайне опасно.
Почему в нулевой провод не разрешается включать предохранитель?
Допустим, в начале стояка установлен предохранитель, но он перегорел (на рисунок 5, г он перечеркнут). В этом случае четырехпроводная схема превращается в трехпроводную со всеми рассмотренными выше недостатками, присущими ей при неравномерной нагрузке фаз.
Согласно Правилам устройства электроустановок (ПУЭ) в начале стояка в нулевой провод не разрешается включать предохранитель (рубильник, автомат). На этажных щитках лестничных клеток, откуда питание расходится по квартирам, предохранители (автоматы) устанавливают только в фазном проводе (рисунок 5, д) либо предохранителей вообще нет. В этом случае, однако, обязателен выключатель В или автомат А, которым вся квартира может быть отсоединена от стояка.
| Рисунок 6. Установочный автомат типа ПАР–10 (предохранитель автоматический резьбовой на ток 10 А), ввертывающийся в предохранитель вместо пробки. 1 – кнопка для включения; 2 – кнопка для отключения. На корпусе автомата написаны его номинальные данные: предельное напряжение сети, например 250 В (эти же автоматы пригодны для сетей 127 и 220 В), и номинальный ток, например 10 А. Номинальный ток может проходить через автомат неограниченно долго. Но при перегрузке (превышении номинального тока) автомат отключается, причем тем скорее, чем перегрузка больше. Короткое замыкание автомат отключает мгновенно. |
Но в квартирах, где к предохранителям П имеют доступ лица, не имеющие специальной электротехнической подготовки, из-за чего не исключено недостаточно хорошее состояние предохранителей, их обязательно устанавливают на обоих проводах, чтобы повысить пожарную безопасность. Не противоречит ли это сказанному выше о недопустимости включать предохранитель в нулевой провод? Нисколько. Потому что нагрузка в пределах квартиры является однофазной, так как по обоим проводам и предохранителям проходит один и тот же ток. Значит перегорание предохранителя в любом проводе (фазном или нулевом – безразлично) не может привести к перекалу ламп: они просто погаснут.
Предохранители в осветительных сетях уступают место установочным автоматам благодаря тому, что автоматы обеспечивают более совершенную защиту и не требуют замены. В новых домах предохранители не применяют. В старых квартирах вместо пробок в предохранители можно установить автоматы (рисунок 6) с резьбовым цоколем, не производя каких-либо монтажных работ.
Сечение нулевого провода в четырехпроводных сетях
обычно меньше сечения фазных проводов. Поэтому в кабелях для четырехпроводных сетей три жилы толще, а одна, предназначенная для нулевого провода, тоньше. Такой кабель обозначается, например, так: 3×16+1×10 (три жилы сечением 16 мм² и одна–сечением 10 мм²). Однако в практике нередко возникает необходимость увеличить сечение нулевого провода. Рассмотрим два примера.
На рисунке 7 показаны три группы I, II, III ламп аварийного освещения, питающиеся в нормальном режиме от вторичной обмотки трансформатора Т (контактор К включен). При исчезновении напряжения переменного тока контактор отключается и лампы автоматически переключаются на аккумуляторную батарею АБ. При этом к проводу 1 (который ранее был нулевым) присоединяется «минус», а к трем проводам 2, 3 и 4 (которые раньше были фазными) присоединяется «плюс». Пока лампы питались от трансформатора, в проводе 1 был небольшой ток, равный геометрической сумме токов в проводах 2, 3 и 4. Когда же лампы переключились на аккумуляторную батарею, ток в проводе 1 стал равен арифметической сумме токов, то есть превысил ток в проводе 2, 3 или 4 примерно в 3 раза. Значит, сечение провода 1 должно быть не меньше, а значительно больше сечения провода 2, 3 или 4.
Рисунок 7. Сечение нулевого провода в схеме аварийного освещения, переключаемого с переменного тока на постоянный, должно быть больше сечения фазного провода.
Приведенный на рисунке 7 пример относится к сравнительно небольшому числу специальных электроустановок (например, к освещению театров и концертных залов).
Следующий пример имеет весьма широкое распространение. Речь идет о питании люминесцентных ламп по четырехпроводной системе. В этих условиях даже при совершенно равномерной нагрузке фаз по нулевому проводу проходят токи высших гармоник, в основном ток третьей гармоники. Этот ток столь значителен, что сечение четвертой жилы обычного четырехжильного кабеля оказывается недостаточным. Рассмотрим этот вопрос подробнее.
На рисунке 8, а показан синусоидальный ток (кривая 1) в фазе А. Такой ток был бы при нагрузке лампами накаливания. При нагрузке люминесцентными лампами дополнительно возникает ток третьей гармоники (кривая 2). Сложение кривых 1 и 2 дает кривую 3, которая показывает, что ток в фазе А несинусоидален. На рисунках 8, б и в изображены кривые для фаз В и С. Сравнивая кривые 2 на рисунках 8, а, б и в, видим, что токи третьих гармоник совпадают по фазе. Поэтому в нулевом проводе они арифметически суммируются, образуя кривую 4 тройной частоты 150 Гц (рисунок 8, г).
Рисунок 8. В нулевом проводе четырехпроводной трехфазной сети, питающей люминисцентные лампы, токи третьих гармоник всех трех фаз алгебраически суммируются, поэтому сечение нулевого провода должно быть увеличено.
В зависимости от схемы включения люминесцентных ламп, их типа, способа компенсации индуктивности балластных дросселей и тому подобного ток в нулевом проводе имеет большую или меньшую величину, но во всяком случае он велик и может даже превысить ток в фазном проводе.
Варианты подключения трехфазной нагрузки
3-х фазные трансформаторы, электродвигатели и другие электроприемники подключаются к выводам генераторов по схеме звезды (γ) либо треугольника (Δ). При этом учитываются следующие особенности:
— линейные и фазные величины напряжений генератора отличаются в 1,732 раза. Uл=√3Uф
;- конструкция электроприемника выполнена для работы с определенным напряжением, называемым номинальным. Его требуется подключать к соответствующим выходным цепям генератора.
Именно поэтому, необходимо выбирать оптимальное соотношение между номинальными величинами напряжений генератора и нагрузки при выборе схемы соединения фаз.
При равенстве номинального напряжения нагрузки, фазным значениям генератора выбирается схема звезды. При этом способе выхода с обмоток приемника подключаются к общей точке «N»
, которую именуют нейтральной либо нулевой.
Входы с обмоток (начала фаз) коммутируют к линейным клеммам 3-х фазного генератора A
,
B
и
C
соединительными проводниками.
Варианты подключения по схеме звезда:
В соединительных проводах между генератором и приемником протекают токи. Их называют линейными токами.
В обмотках приемников тоже протекают токи, которые получили название фазных. Их направление от начала (входа в обмотку) к концу (выходу) считается положительным (+).
При последовательном подключении фаз нагрузки к линейным проводам генератора в образовавшейся цепи циркулируют одни и те же электротоки IА, IВ и IС
. Они в схеме звезды равны для линии и обмоток приемника, другими словами:
Iл= Iф
.
У схемы звезды с нулевым проводом в нейтрали протекает нулевой (не значит, что его значение равно нулю) или нейтральный ток, обозначаемый IN
.
Возникающую при прохождении тока разность потенциалов между началом и окончанием каждой обмотки в приемнике называют фазным напряжением, обозначают UАN, UBN и UCN
.
Разности потенциалов между точками подключения начала фаз называют линейными напряжениями, обозначают UАВ
,
UBС
и
UCА
. Их значения одинаковы для генератора и нагрузки.
У электроприемников схемы звезды с нулевым проводником для любой обмотки подключается соответствующее фазное напряжение от генератора. Оно обозначается для фазы:
А: UАN=UАN= UА; В: UВN=UВN=UВ; С: UСN=UСN=UС.
Любая фаза работает самостоятельно, не зависит от других. В ней токи (линейные или фазные) определяют формулой по закону Ома:
IА=UА/ZА; IВ=UВ/ZВ; IС=UС/ZС
.
Первый закон Кирхгофа позволяет определить ток в нейтральном проводе как геометрическую сумму линейных либо фазных токов выражением: IN=IA+IB+IC
.
При равных и симметричных нагрузках (ZA=ZB=ZC)
величина тока в нейтральном проводе равна нулю. IN=0. Поэтому, симметричные 3-х фазные электроприемники (электродвигатели) подключают без нейтрального провода.
Для случая нарушения симметрии нагрузки характерно появление в нулевом проводнике тока, величина которого определяется отличиями от симметричных составляющих.
Такие отклонения снижают на стадии проекта и производства, чем и объясняются незначительные величины токов в нулевом проводе по сравнению с фазными/линейными значениями.
Описываемые 1-м законом Кирхгофа соотношения токов для любых нагрузок схем звезды без нулевого провода (IA+IB+IC=0)
определяют взаимозависимость векторов.
Изменение одного любого вектора ведет к одновременному преобразованию остальных, чем проявляется зависимость режима. Ток нейтрали формирует разность потенциалов с величиной отличной от нуля.
На комплексной плоскости напряжение нулевой последовательности изображается вектором Un
, смещающим центральную точку соединения векторов фазных напряжений для приемника
(UАN, UВN, UСN)
, которые теряют равенство с фазными напряжениями генератора
(UА, UВ, UС)
. Возникает перекос с фазными напряжениями у приемника.
Способ расчета векторов тока и напряжения для схемы звезды без нулевого провода
. Методом 2-х узлов вычисляются параметры смещения нейтральной точки для вектора напряжения нейтрали
(UN)
:
ZN
– значение комплексного сопротивления нейтрального провода. Для схемы без нулевого провода
ZN=∞
.
Определение фазных напряжений основано на вычислении разности потенциалов между началами и окончаниями обмоток:
UАN=UА-UN; UВN=UВ-UN; UСN=UС-UN
.
Расчеты фазных токов внутри приемника производятся на основе закона Ома:
Величина тока в нейтральном проводнике вычисляется геометрической суммой входных линейных/фазных токов на основе 1-го закона Кирхгофа:
IN=IA+IB+IC.
Формулы для расчета полной мощности в фазах:
При разных нагрузках в фазах возникает перекос напряжений в схеме, который может привести к неисправностям. Поэтому, эксплуатировать такие нагрузки в схемах электроприемников без нулевого провода (часто это коммутируемые цепи освещения, обогрева и др.) запрещено.
Способ расчета векторов тока и напряжения для схемы треугольника
. При равенстве значений номинальных напряжений электроприемника величинам линейных напряжений генератора используется схема треугольника.
Для ее создания в приемнике выход одной обмотки подключается ко входу другой с выводом точки коммутации (являющейся вершиной треугольника) на клемму для соединения проводами с линейным выводом 3-х фазного генератора. Так формируются подключения к фазам А, В, С
.
В обмотках такого приемника проходят фазные токи IАB, IBC, ICА
. А токи, подводимые к приемнику от генератора по проводам, называют линейными. Их обозначают
IА, IB, IC
.
Для рассматриваемой цепи выполняется равенство подводимых напряжений с линии фазным напряжениям приемника UАB, UBC, UCА
. Каждая отдельная фаза работает самостоятельно без зависимости от остальных.
Расчет фазных токов проводится по закону Ома:
Вектора линейных токов описываются 1-м законом Кирхгофа в точках вершин треугольника и вычисляются как геометрическая разность векторов в фазах:
IА=IАB-IСА; IВ=IBС-IАВ; IC=IСА-IВС.
Для симметричного режима нагрузок выполняется симметричность фазных и линейных токов, которые определяются соотношением Iл=√3Iф
. При несимметричном режиме нагрузок соотношения векторов линейных и фазных описываются 1-м законом Кирхгофа.
Примерное соотношение векторов для произвольной 3-х фазной цепи, работающей по схеме треугольник на комплексной плоскости, представлено на векторной диаграмме.
Соединение в звезду обмоток трансформаторов
На рисунке 9, а дан пример соединения генератора Г, трех трансформаторов Т1, Т2, Т3, электродвигателя Д и однофазных нагрузок Н. В данном примере обмотки генератора, трансформаторов и электродвигателя соединены в звезду. Нетрудно видеть, что первичная обмотка трансформатора Т1 является электроприемником для генератора Г, вторичная обмотка трансформатора Т1 служит источником тока для первичной обмотки трансформатора Т2. Вторичная обмотка трансформатора Т2 – источник тока для первичной обмотки трансформатора Т3. Его вторичная обмотка – источник тока для электродвигателя Д и нагрузок Н.
Рисунок 9. Соединение в звезду трансформаторов.
Сравнение схем трансформаторов Т1, Т2 и ТЗ показывает, что они неодинаковы. Так, нейтральная точка первичной обмотки трансформатора Т1 заземлена и, следовательно, соединена с заземленной нейтральной точкой генератора Г. Нейтральные точки обмоток трансформатора Т2 не выведены. У трансформатора ТЗ выведена нейтральная точка вторичной обмотки, но от земли она изолирована. Конечно, соединения, показанные на рисунке 9, а, вовсе не обязательны, они даны здесь только для иллюстрации типичных случаев соединений в звезду.
Рисунки 9, б и в соответственно показывают, что в звезду можно соединить как три однофазных трансформатора, так и один трехфазный трансформатор.
На рисунке 9, г даны примеры различных соединений обмоток трансформаторов в звезду. Здесь буквы A, B, C – начала, а X, Y, Z – концы обмоток высшего напряжения (ВН); a, b, c и x, y, z – начала и концы обмоток низшего напряжения (НН). Рисунок 9, д иллюстрирует соединения в звезду с выведенной нейтралью обмотки ВН (слева), обмотки НН (в центре) и обеих обмоток (справа).
Ограничимся пока общим замечанием о том, что не все способы соединения трансформаторов в звезду равноценны. Различие в них определяется рядом причин, которые нельзя объяснить сразу, и поэтому они выяснятся в ходе дальнейшего изложения.
Заземление нейтрали
В старых выпусках ПУЭ указывалось, что городские электрические сети напряжением выше 1000 В должны выполняться трехфазными с изолированной нейтралью, а распределительные сети в новых городах – трехфазными четырехпроводными с наглухо заземленной нейтралью при напряжении 380 / 220 В. Однако существуют также сети напряжением 220 / 127 В, причем их нейтраль изолирована. При изолированной нейтрали применяют пробивные предохранители.
Обмотки силовых трансформаторов отечественных заводов напряжением 110 кВ и выше выполняют для работы с заземленной нейтралью, так как они имеют неполную изоляцию со стороны нулевых выводов.
Заземление нейтрали и безопасность
Поясним вкратце, зачем в сетях до 1000 В заземляют нейтраль, по каким причинам иногда отдают предпочтение изолированной нейтрали, для чего служат пробивные предохранители.
На рисунке 10, а показаны вторичные обмотки трансформатора Т, питающие четырехпроводную сеть напряжением 380 / 220 В, нейтраль которой изолирована. Пусть в рассматриваемый момент изоляция совершенно исправна. Тем не менее на рисунке показаны три сопротивления r, соединенные в звезду. Ее нейтралью является земля. Эти сопротивления условно изображают несовершенство изоляции проводов, которая в какой-то степени все же проводит ток. На этом же рисунке показаны три конденсатора C, соединенные в звезду. Ее нейтралью также служит земля. Конденсаторы условно изображают электрическую емкость проводов относительно земли, что в электроустановках переменного тока весьма важно, так как емкость проводит ток.
Рисунок 10. Потенциал нейтрали. Заземления в трехфазных системах.
Какие же напряжения имеются в рассматриваемой электроустановке? Между линейными проводами 380 В, между каждым линейным проводом и нейтралью трансформатора 220 В, между каждым линейным проводом и землей 220 В. Почему? Потому что земля оказалась нейтралью звезд из трех равных сопротивлений r и трех равных емкостей C. А если линейный провод относительно нейтрали трансформатора имеет такое же напряжение, как и относительно земли, то ясно, что между нейтралью трансформатора и землей напряжение равно нулю 3.
Прикосновение человека, стоящего на земле, к одному из линейных проводов небезопасно, так как через несовершенную изоляцию, емкости проводов и тело человека проходит ток. В один из моментов времени его направление показано на рисунке 10, б. Сила тока, а следовательно, и степень опасности определяются значениями сопротивлений, емкостей и фазным напряжением. Иными словами, в данном случае человек находится под напряжением 220 В.
Но что произойдет, если один из линейных проводов заземлится, а человек, стоящий на земле, прикоснется к другому линейному проводу? Из рисунка 10 в, видно, что человек окажется теперь не под фазным, а под линейным напряжением 380 В, что значительно опаснее.
В сетях с заземленной нейтралью человек, стоящий на земле и прикоснувшийся к линейному проводу, попадает под фазное напряжение (рисунок 10, г). Если при этом заземлится другой линейный провод (рисунок 10, д), то предохранитель перегорит, но повышения напряжения с фазного до линейного (как в сетях с изолированной нейтралью) не будет.
Это значит, что как в сети 380 / 220 В с заземленной нейтралью, так и в сети 220 / 127 В с изолированной нейтралью человек, касающийся оголенного провода, может попасть под напряжение 220 В. Но сети 380 / 220 В выгоднее сетей 220 / 127 В, так как для передачи одинаковой мощности при 380 / 220 В нужны провода меньшего сечения.
Предупреждение. Для обеспечения безопасности заземления следует выполнять, строго соблюдая, ряд требований. Этому специальному вопросу уделено особое внимание в ПУЭ, посвящен ряд книг, и в их числе книги М. Р. Найфельда «Заземление и другие защитные меры» и П. А. Долина «Действие электрического тока на тело человека и первая помощь пострадавшему».
Сравнения схем подключения между собой
Чтобы сравнить обе схемы между собой, надо посчитать электрическую мощность, развиваемую электродвигателем при том или ином включении. Для этого надо рассмотреть понятия линейного (Iлин) и фазного (Iфаз) токов. Фазным током называется ток, протекающий по обмотке фазы. Линейный ток протекает по проводнику, подключенному к выводу обмотки.
В сетях до 1000 вольт источником электричества является трансформатор, вторичная обмотка которого включена «звездой» (в противном случае невозможно организовать нулевой провод) или генератор, обмотки которого соединены по той же схеме.
Из рисунка видно, что при соединении «звездой» токи в проводниках и токи в обмотках электродвигателя равны. Ток в фазе определяется фазным напряжением:
где Z – сопротивление обмотки одной фазы, их можно принять равными. Можно записать, что
.
Для соединения «треугольником» токи другие – они определяются линейными напряжениями, приложенными к сопротивлению Z:
.
Следовательно, для данного случая .
Теперь можно сравнить полную мощность (), потребляемую электродвигателями с разной схемой.
- для соединения «звездой» полная мощность равна ;
- для соединения «треугольником» полная мощность равна .
Таким образом, при включении «звездой» электродвигатель развивает мощность в три раза ниже, чем при соединении в треугольник. Это также ведет к другим положительным последствиям:
- уменьшаются пусковые токи;
- работа двигателя и его пуск становятся более плавными;
- электромотор хорошо справляется с кратковременными перегрузками;
- тепловой режим асинхронного двигателя становится более щадящим.
Обратная сторона медали – двигатель с обмотками «звездой» не может развивать максимальную мощность. В некоторых случаях вращающего момента может не хватить даже для раскрутки ротора.
Пробивной предохранитель
Нарушение изоляции между обмотками высшего и низшего напряжений (ВН и НН) трансформатора может привести к массовому пробою изоляции в сетях низшего напряжения и поражению людей. Чтобы предотвратить эти опасные явления в сетях с изолированной нейтралью, применяют пробивные предохранители. Пробивной предохранитель включают между нейтралью трансформатора и землей при соединении в звезду (рисунки 11, а и в) или между одним из фазных проводов и землей при соединении в треугольник (смотрите статью «Схема соединения «Треугольник»), как показано на рисунке 11, б.
Рисунок 11. Пробивные предохранители в сетях с изолированной нейтралью.
В пробивном предохранителе одна токоведущая деталь присоединена к нейтрали (фазе) трансформатора, другая заземлена, но между ними помещена слюдяная прокладка с отверстиями. При нормальном напряжении прокладка надежно изолирует нейтраль (фазу) от земли. Однако при переходе высшего напряжения на обмотку низшего напряжения пробивной предохранитель пробивается и заземляет обмотки.
При глухом заземлении нейтрали пробивной предохранитель не нужен.
Фазные и линейные напряжения
Для понимания различий между способами соединения обмоток, сначала надо разобраться с понятиями фазных и линейных напряжений. Фазным напряжением называется напряжение между началом и концом одной фазы. Линейным – между одинаковыми выводами разных фаз.
Для трехфазной сети линейные напряжения – это напряжения между фазами, например, А и В, а фазные – между каждой фазой и нулевым проводником.
Так напряжения Ua, Ub, Uc будут фазными, а Uab, Ubc, Uca – линейными. Различаются эти напряжения в раз. Так, для бытовой и промышленной сети 0,4 кВ линейные напряжения равны 380 вольт, а фазные – 220 вольт.
Заземление нейтрали и бесперебойность электроснабжения
Кроме условий безопасности есть и другой важный вопрос, а именно: бесперебойность электроснабжения потребителей, при решении которого небезразлично, заземлять нейтраль или ее изолировать. Существо дела сводится к следующему.
В сети с изолированной нейтралью при заземлении линейного провода предохранители не перегорают (автомат не отключается), так как короткого замыкания нет. Между линейными проводами, а также между линейными проводами и нейтралью трансформатора сохраняются нормальные напряжения и потребители электроэнергии могут некоторое время продолжать работу.
В сети с заземленной нейтралью нарушение изоляции линейного провода приводит к короткому замыканию, предохранители перегорают или отключается автомат, работа потребителей нарушается. Значит, бесперебойность электроснабжения выше в сетях с изолированной нейтралью.
Необходимо особо подчеркнуть следующие важнейшие обстоятельства:
а) Хотя в сетях с изолированной нейтралью возможна работа потребителей, но такой режим опасен для изоляции других фаз и присоединенного к ним оборудования. Дело в том, что при металлическом замыкании на землю одной из фаз напряжение других фаз по отношению к «земле» возрастает в 1,73 раза по сравнению с нормальным напряжением, а напряжение нулевой точки смещается и становится равным фазному напряжению относительно земли. Действительно, при заземлении провода (рисунок 12, а) линейные напряжения AB, BC, CA остаются теми же; не изменяются и фазные напряжения A0, B0, C0. Но по отношению к «земле» напряжения изменяются. Для фаз A и C они повышаются до величин AB и BC соответственно. Для фазы B напряжение по отношению к земле снижается до нуля. Напряжение нейтрали относительно земли возрастает от нуля до величины 0B, равной фазному напряжению.
Рисунок 12. Смещение нейтрали в сети с изолированной нейтралью при аварийных режимах. а – заземление фазы; б – короткое замыкание на нагрузке одной из фаз; в – обрыв фазы.
Если замыкание происходит через дугу, то перенапряжения могут в 2–2,5 раза превысить фазное напряжение. Через место замыкания пойдут емкостные токи всех фаз, которые при протяженных кабельных линиях велики и могут вызвать нагревы в местах нарушения изоляции. Поэтому на электрических станциях и подстанциях нередко имеются устройства, непрерывно контролирующие состояние изоляции относительно земли. Принцип их действия рассмотрен в статьях «Разомкнутый треугольник. Открытый треугольник» и «Примеры соединений измерительных трансформаторов».
б) Если нейтраль нагрузки 0′ не соединена с нейтралью 0 вторичной обмотки трансформатора (рисунок 12, б), то при коротком замыкании одной фазы потенциал линейного провода B попадает в нейтраль 0′ нагрузки. Это значит, что нагрузка, присоединенная к фазам A и C, окажется под значительно повышенным напряжением (линейным вместо фазного).
в) Если нейтраль нагрузки 0′ не соединена с нейтралью 0 вторичной обмотки трансформатора (рисунок 12, в) и в одной фазе, например в фазе B, перегорит предохранитель (перечеркнут), то на нагрузках фаз A и C напряжение понизится и станет 220 В / 2 = 110 В вместо 220 / √3 = 127 В (рассматривается сеть 220 / 127 В). Напряжение на зажимах перегоревшего предохранителя будет в 1,5 раза больше фазного, то есть составит 127 × 1,5 = 190 В.
Несимметричный режим трехфазных цепей
| • Трехфазные цепи • |
- Трехфазные системы
- Соединение обмоток генератора звездой
- Соединение обмоток генератора треугольником
- Соединение приемников энергии звездой
- Соединение приемников энергии треугольником
- Несимметричный режим трехфазных цепей
- …
| • Обзор сайта • |
- Электрооборудование до 1000 В
- Электрические аппараты
- Электрические машины
- Эксплуатация электро оборудования
- Электрооборудование электротехнологических установок
- Электрооборудование общепромышленных установок
- Электрооборудование подъемно-транспортных установок
- Электрооборудование металлообрабатывающих станков
- Электрооборудование выше 1000 В
- Электрические аппараты высокого напряжения
- Электротехника
- Электрическое поле
- Электрические цепи постоянного тока
- Электромагнетизм
- Электрические машины постоянного тока
- Основные понятия,отно сящиеся к переменным токам
- Цепи переменного тока
- Трехфазные цепи
- Электротехнические измерения и приборы
- Трансформаторы
- Электрические машины переменного тока
- Электромонтаж
- С чего начинается электро монтаж энергоснабжения электрооборудования и электропроводки
- Монтаж электропроводки
- Расчёт потребляемой мощ ности,сечения кабеля и номинала автоматического выключателя
- Электромонтажные работы и прокладка кабеля в жилых и нежилых помещениях
- Электромонтажные работы по расключению распаечных коробок и электрооборудова ния
- Электромонтаж и заземле ние розеток
- Электромонтаж уравнива ния потенциалов
- Электромонтаж контура заземления
- Электромонтаж модульного штыревого контура заземле ния
- Электромонтаж нагреватель ного кабеля для подогрева полов
- Электромонтажные работы по прокладке кабеля в зем ле
- Электричество в частном доме
- Проект электроснабжения
| • Электротехника • |
- Электрическое поле
- Электрические цепи постоянного тока
- Электромагнетизм
- Электрические машины постоянного тока
- Основные понятия,отно сящиеся к переменным токам
- Цепи переменного тока
- Трехфазные цепи
- Электротехнические измерения и приборы
- Трансформаторы
- Электрические машины переменного тока
- …
ЭЛЕКТРОСПЕЦ
ЭЛЕКТРОСПЕЦ
а) Назначение нулевого провода. При несимметричной нагрузке звездой без нулевого провода (на рис. 11.19 ключ разомкнут) сопротивления всех фаз неодинаковы: ZА ZВ ZС . Вследствие этого появляется напряжение смещения нейтрали UN’N , определяемое по формуле двух узлов:
Это напряжение UN, действующее между точками N и N’ (рис. 11.19), показано на рис. 11.20. При любом направлении вектора UN напряжения на фазах нагрузки будут неодинаковы.
При включении и выключении приемников проводимости фаз YА, YB и YC изменяются произвольным образом, это приводит к изменению напряжения смещения нейтрали UN, ведущее, в свою очередь, к произвольному изменению напряжений на фазах нагрузки. Подавляющее большинство электросиловых приемников функционирует только при номинальном питающем напряжении. Поэтому соединение звездой без нулевого провода для несимметричной или изменяемой нагрузки практически не используется вследствие невозможности обеспечить номинальное питающее напряжение. При большом числе приемников, статистически в «среднем» обеспечивающих примерно одинаковую нагрузку фаз, несмотря на включение и выключение отдельных потребителей, смещение нейтрали невелико. Это позволяет использовать соединение звездой без нулевого провода для мощных линий электропередач на трансформаторные подстанции напряжением до 6,3 кВ. Соединение звездой без нулевого провода используется и в устройствах, предназначенных для контроля и анализа режимов трехфазных цепей.
б) Соединение звездой с нулевым проводом. Для соединения звездой с нулевым проводом (на рис. 11.19 ключ замкнут) определим напряжение нейтрали также по формуле двух узлов:
В реальных системах электроснабжения проводимость нулевого провода YN много больше проводимостей фаз и практически можно считать, что сопротивление нулевого провода близко к нулю. Тогда при YN→ ∞ знаменатель в выше написанной формуле стремится к бесконечности, UN→ 0 и при наличии нулевого провода с достаточно малым сопротивлением смещение потенциала нулевой точки N’ нагрузки отсутствует. На фазах нагрузки независимо от их сопротивлений поддерживаются напряжения, составляющие симметричную трехфазную систему. Токи фаз нагрузки определяются по закону Ома:
На рис. 11.22 показана векторная диаграмма токов при несимметричной активной нагрузке. Из векторной диаграммы видно, что токи фаз при несимметричной нагрузке не равны по модулю, а в общем случае смещены по фазе на углы, не равные 120°, т. е. они не представляют симметричную трехфазную систему. Ток нейтрального провода (см. рис. 11.14) можно определить по первому закону Кирхгофа для узла N’ — рис. 11.22 (на рисунке изображен вспомогательный вектор тока, равный сумме токов IА+ IС):
Чем больше несимметрия фаз нагрузки, тем больше «уравнительный» ток IN нулевого провода.
Соединение звездой с нулевым проводом повсеместно используется для электропитания жилых и общественных зданий, производственных приемников энергии и в других случаях с многочисленными приемниками, включаемыми и выключаемыми независимо друг от друга.
в) Соединение треугольником. Если пренебречь сопротивлением соединительных проводов, то напряжения на фазах нагрузки равны линейным напряжениям трехфазного источника . Фазные токи при несимметричной нагрузке ZАB ZВС ZСA определяются по закону Ома:
На рис. 11.25 показана векторная диаграмма токов при несимметричной активной нагрузке. Линейные токи определяются по первому закону Кирхгофа для узлов А, В и С рис. 11.17:
Как видно из векторной диаграммы (рис. 11.25), линейные токи не равны по модулю и смещены по фазе на углы, не равные 120°. В общем случае и фазные токи не равны по модулю и смещены по фазе на углы, не равные 120°.
Векторная диаграмма линейных токов показана на рис. 11.25.
г) Аварийные режимы в трехфазных цепях. Частными случаями несимметричных режимов являются аварийные режимы в трехфазных цепях: обрывы нейтрального и линейных проводов, КЗ в фазах. Абсолютно безопасными являются разрывы в фазах нагрузки, соединенной треугольником или звездой с нулевым проводом (отключения фаз) Аварийными, пожароопасными являются КЗ фаз нагрузки таких соединений. Все другие случаи приводят к резкому изменению номинальных напряжений на фазах нагрузки и могут привести к аварийной ситуации. Обрыв нулевого провода несимметричной звезды был рассмотрен в примере 11.9.