Частота колебаний - определение, формулы и характеристики

Количество повторений или циклов в единицу времени

Для использования в других целях см. Частота (значения).

«Частоты» перенаправляются сюда. О фильме см. Частоты (фильм). Об альбоме см. Частоты (альбом).

Для более широкого освещения этой темы см. Временная ставка.

Частота
Общие символы	ж , ν
Единица СИ
В Базовые единицы СИ	−1
Измерение	Т − 1 {displaystyle {mathsf {T}} ^ {- 1}}

Частота

количество повторений повторяющегося события на единица времени.[1] Его также называют
временная частота
, что подчеркивает контраст пространственная частота и угловая частота. Частота измеряется в единицах герц (Гц), что соответствует одному повторению события в секунду. В
период
это продолжительность одного цикл в повторяющемся событии, поэтому период — это взаимный частоты.[2] Например: если сердце новорожденного ребенка бьется с частотой 120 раз в минуту (2 герца), его период,
Т
, — временной интервал между ударами — полсекунды (60 секунд разделить на 120 удары). Частота — важный параметр, используемый в науке и технике для определения скорости колебательный и вибрирующий явления, такие как механические колебания, звуковые сигналы (звук), радиоволны, и свет.

Определения

Эти три точки мигают, или кататься на велосипеде
, периодически — от наименьшей частоты (0,5 Гц) до максимальной частоты (2,0 Гц), сверху вниз. Для каждой мигающей точки: «f» — это частота в герц, (Гц) — или количество событий в секунду (циклов в секунду), когда точка мигает; пока «Т» — это то
период
, или же
время
, в секундах (с) каждого цикла (количество секунд на цикл). Примечание Т и транспортные расходы взаимные ценности друг другу. По прошествии времени — здесь, двигаясь слева направо по горизонтальной оси — пять синусоидальные волны меняться или меняться, регулярно в разные тарифы. Красный волна (вверху) имеет самую низкую частоту (циклы с самой медленной скоростью), а пурпурная волна (внизу) имеет самую высокую частоту (циклы с максимальной скоростью).

За циклический процессы, такие как вращение, колебания, или же волны, частота определяется как количество циклов в единицу времени. В физика и инженерное дело дисциплины, такие как оптика, акустика, и радио, частота обычно обозначается латинской буквой ж

или греческой буквой
ν {displaystyle u}
или же
ν
(ню) (см., например, Формула планка).

Связь между частотой и периодом, Т {displaystyle T} , повторяющегося события или колебания определяется выражением

ж = 1 Т . {displaystyle f = {frac {1} {T}}.}

Примеры движения

Колебательное движение является одним из наиболее распространенных в природе. Например, можно представить себе струны музыкальных инструментов, качели или голосовые связки человека.

В физике колебаниями называются процессы, которые повторяются через равные промежутки времени. Подобные движения рассматривается посредством нескольких моделей:

тела, подвешенного на пружине (двигающееся по направлению вверх-вниз);
груза на нитке;
электрического контура и других.

Единицы

В Производная единица СИ частоты — это герц (Гц), названный в честь немецкого физика Генрих Герц. Один герц означает, что событие повторяется один раз в второй. Если частота обновления телевизора составляет 1 герц, экран телевизора будет менять (или обновлять) изображение один раз в секунду. Предыдущее название этого подразделения было циклов в секунду (cps). В единица за период — вторая.

Традиционной единицей измерения вращающихся механических устройств является число оборотов в минуту, сокращенно об / мин или об / мин. 60 оборотов в минуту равны одному герцу.[3]

Амплитуда и фаза колебаний

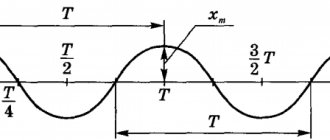
Амплитуда колебаний – модуль наибольшего смещения тела от положения равновесия. Обозначение – $ A\, (X_{max}) $, единицы измерения – м.

Фаза колебаний – это величина, которая определяет состояние колебательной системы в любой момент времени. Обозначение – $ \varphi $, единицы измерения – рад (радиан).

Фаза колебаний – это величина, стоящая под знаком синуса или косинуса. Она показывает, какая часть периода прошла от начала колебаний. Фаза гармонических колебаний в процессе колебаний изменяется. $ \varphi_0 $ – начальная фаза колебаний. Начальная фаза колебаний – величина, которая определяет положение тела в начальный момент времени.

Важно! Путь, пройденный телом за одно полное колебание, равен четырем амплитудам.

Период против частоты

Для удобства длинные и медленные волны, такие как океанские поверхностные волны, как правило, описываются периодом волны, а не частотой. Короткие и быстрые волны, как аудио и радио, обычно описываются их частотой, а не периодом. Эти часто используемые преобразования перечислены ниже:

Частота	1 мГц (10−3 Гц)	1 Гц (100 Гц)	1 кГц (103 Гц)	1 МГц (106 Гц)	1 ГГц (109 Гц)	1 ТГц (1012 Гц)
Период	1 кс (103 s)	1 с (100 s)	1 мс (10−3 s)	1 мкс (10−6 s)	1 нс (10−9 s)	1 шт. (10−12 s)

Содержание

1 Определения и единицы
2 Период против частоты
3 Связанные типы частоты
4 При распространении волн
5 Измерение 5.1 Подсчет
5.2 Стробоскоп
5.3 Частотомер
5.4 Гетеродинные методы

6 Примеры

6.1 Свет

6.2 Звук

6.3 Линейный ток

7 Апериодическая частота

8 См. Также

9 Примечания

10 Ссылки

11 Источники

12 Дальнейшее чтение

13 Внешние ссылки

Связанные типы частоты

Для использования в других целях см. Частота (значения).

Диаграмма взаимосвязи между различными типами частоты и другими свойствами волн.

Угловая частота, обычно обозначается греческой буквой ω (омега), определяется как скорость изменения угловое смещение, θ
, (во время вращения), или скорость изменения фаза из синусоидальный формы волны (особенно в колебаниях и волнах), или как скорость изменения аргумент к функция синуса:

у ( т ) = грех ⁡ ( θ ( т ) ) = грех ⁡ ( ω т ) = грех ⁡ ( 2 π ж т ) {displaystyle y (t) = sin left (heta (t) ight) = sin (omega t) = sin (2mathrm {pi} ft)} d θ d т = ω = 2 π ж {displaystyle {frac {mathrm {d} heta} {mathrm {d} t}} = omega = 2mathrm {pi} f} Угловая частота обычно измеряется в радианы в секунду (рад / с), но для сигналы с дискретным временем, также можно выразить в радианах на интервал выборки, который является безразмерная величина. Угловая частота (в радианах) больше обычной частоты (в Гц) в 2π раз.

Пространственная частота аналогична временной частоте, но ось времени заменяется одной или несколькими осями пространственного смещения. Например.:

у ( т ) = грех ⁡ ( θ ( т , Икс ) ) = грех ⁡ ( ω т + k Икс ) {displaystyle y (t) = sin left (heta (t, x) ight) = sin (omega t + kx)} d θ d Икс = k {displaystyle {frac {mathrm {d} heta} {mathrm {d} x}} = k} Волновое число, k
, является пространственно-частотным аналогом угловой временной частоты и измеряется в радианах на метр. В случае более чем одного пространственного измерения волновое число является вектор количество.

Понятие скорости

Когда мы сравниваем движение каких-либо тел, то говорим, что одни тела двигаются быстрее, а другие — медленнее. Такую простую терминологию мы используем в повседневной жизни, говоря, например, о движении транспорта. В физике быстрота движения тел характеризуется определенной величиной. Эта величина называется скоростью. Общее определение скорости (в случае, если тело движется равномерно):

Скорость при равномерном движении тела — это физическая величина, показывающая, какой путь прошло тело за единицу времени.

Под равномерным движением тела подразумевается, что скорость тела постоянна. Формула нахождения скорости: $v=frac$, $s$ — это пройденный телом путь (то есть длина линии), $t$ — время (то есть промежуток времени, за который пройден путь).

Согласно международной системе СИ, единица измерения линейной скорости является производной от двух основных единиц — метра и секунды, то есть измеряется в метрах в секунду (м/с). Это значит, что под единицей скорости понимается скорость такого равномерного движения, при котором путь в один метр тело проходит за одну секунду.

Попробуй обратиться за помощью к преподавателям

Также скорость часто измеряют в км/ч, км/с, см/с.

Рассмотрим простой пример задачи на вычисление скорости.

Задача. Двигаясь равномерно, поезд за 4 ч проходит 219 км. Найти его скорость движения.

Решение. $v=frac<219 км><4 ч>=54,75frac<�км><�ч>$. Переведём километры в метры и часы в секунды: $54,75frac<�км><�ч>=frac<54750 м><3600c>approx 15,2frac<�м>$.

Из примера мы видим, что числовое значение скорости отличается в зависимости от выбранной единицы измерения.

Кроме числового значения, скорость имеет направление. Числовое значение величины в физике называют модулем. Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость — это векторная физическая величина.

На письме модуль скорости обозначается $v$, а вектор скорости — $vec v$.

В свою очередь, такие величины как путь, время, длина и другие характеризуются только числовым значением. Тогда говорят, что это скалярные физические величины.

Читать также: Когда проходить первое то

Задай вопрос специалистам и получи ответ уже через 15 минут!

В случае, когда движение является неравномерным, используют понятие средней скорости. Формула средней скорости: $v_<�ср>=frac$, где $s$ — это весь пройденный телом путь, $t$ — всё время движения. Рассмотрим пример задачи на среднюю скорость, чтобы понять разницу.

Задача. Некоторый транспорт за 2,5 часа преодолевает путь в 213 км. Найти его $v_<�ср>$.

Ответ. $85,2 frac<�км><�ч>$ или $23,7frac<�м> <�с>$.

При распространении волн

Дальнейшая информация: Распространение волн

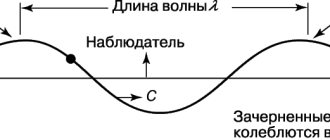
Для периодических волн в недисперсные среды (то есть среды, в которой скорость волны не зависит от частоты), частота имеет обратную зависимость от длина волны, λ

(лямбда). Даже в диспергирующих средах частота
ж
синусоидальной волны равна фазовая скорость
v
из волна разделенный по длине волны
λ
волны:
ж = v λ . {displaystyle f = {frac {v} {lambda}}.}
в особый случай электромагнитных волн, движущихся через вакуум, тогда v = c

, куда
c
это скорость света в вакууме, и это выражение становится:
ж = c λ . {displaystyle f = {frac {c} {lambda}}.}
Когда волны из монохромный исходное путешествие из одного средний для другого их частота остается той же — только их длина волны и скорость изменять.

Пружинный маятник

Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.

Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.

Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:

F=-kx.

Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.

По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.

После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.

Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.

Измерение

Смотрите также: Частотомер

Измерение частоты можно выполнить следующими способами:

Подсчет

Вычисление частоты повторяющегося события выполняется путем подсчета количества раз, когда это событие происходит в течение определенного периода времени, а затем деления этого числа на продолжительность периода времени. Например, если в течение 15 секунд произошло 71 событие, частота будет:

ж = 71 15 s ≈ 4.73 Гц {displaystyle f = {frac {71} {15, {ext {s}}}} приблизительно 4,73, {ext {Hz}}}

Если количество отсчетов не очень велико, точнее измерить временной интервал для заранее определенного количества появлений, чем количество повторов в течение определенного времени.[4] Последний метод вводит случайная ошибка на счет от нуля до единицы и т. д. средний полсчета. Это называется ошибка стробирования

и вызывает среднюю ошибку в вычисленной частоте Δ ж = 1 2 Т м {displaystyle Delta f = {frac {1} {2T_ {m}}}} , или дробная ошибка Δ ж ж = 1 2 ж Т м {displaystyle {frac {Delta f} {f}} = {frac {1} {2fT_ {m}}}} куда Т {displaystyle T} это временной интервал и ж {displaystyle f} — измеренная частота. Эта ошибка уменьшается с частотой, поэтому обычно возникает проблема на низких частотах, когда количество отсчетов
N
маленький.

Частотомер с резонансным язычком, устаревшее устройство, которое использовалось примерно с 1900 по 1940-е годы для измерения частоты переменного тока. Он состоит из полосы металла с язычками разной длины, которые колеблются электромагнит. Когда неизвестная частота применяется к электромагниту, язычок резонансный на этой частоте будет вибрировать с большой амплитудой, видимой рядом со шкалой.

Стробоскоп

Более старый метод измерения частоты вращения или вибрации объектов заключается в использовании стробоскоп. Это интенсивный, периодически мигающий свет (импульсная лампа), частоту которого можно отрегулировать с помощью откалиброванной схемы синхронизации. Стробоскоп направлен на вращающийся объект, а частота регулируется вверх и вниз. Когда частота строба равна частоте вращающегося или вибрирующего объекта, объект завершает один цикл колебаний и возвращается в исходное положение между вспышками света, поэтому при освещении стробоскопом объект кажется неподвижным. Затем частоту можно будет считать по откалиброванным показаниям на стробоскопе. Обратной стороной этого метода является то, что объект, вращающийся с целым кратным частоте стробирования, также будет казаться неподвижным.

Частотомер

Основная статья: Частотомер

Современный частотомер

Более высокие частоты обычно измеряются с помощью частотомер. Это электронный инструмент который измеряет частоту применяемых повторяющихся электронных сигнал и отображает результат в герцах на цифровой дисплей. Оно использует цифровая логика для подсчета количества циклов в течение интервала времени, установленного точностью кварц временная база. Циклические процессы, которые не являются электрическими, такие как скорость вращения вала, механические колебания или звуковые волны, может быть преобразован в повторяющийся электронный сигнал с помощью преобразователи и сигнал подается на частотомер. По состоянию на 2022 год частотомеры могут охватывать диапазон примерно до 100 ГГц. Это представляет собой предел прямых методов подсчета; частоты выше этого должны быть измерены косвенными методами.

Гетеродинные методы

За пределами диапазона частотомеров частоты электромагнитных сигналов часто измеряются косвенно с использованием гетеродинирование (преобразование частоты). Опорный сигнал известной частоты, близкой к неизвестной, смешивается с неизвестной частотой в нелинейном смесительном устройстве, таком как диод. Это создает гетеродин или «бить» сигнал по разнице между двумя частотами. Если два сигнала близки по частоте, гетеродин достаточно низкий, чтобы его можно было измерить частотомером. Этот процесс только измеряет разницу между неизвестной частотой и опорной частотой. Для достижения более высоких частот можно использовать несколько этапов гетеродинирования. Текущие исследования распространяют этот метод на инфракрасные и световые частоты (оптическое гетеродинное обнаружение).

Явление резонанса

Это понятие имеет особое значение для описания колебаний. Если имеется некое воздействие, частота которого приближается к собственной частоте системы, то последняя реагирует резким увеличением амплитуды.

Явление резонанса можно представить себе на примере того же математического маятника. Для этого необходимо маятник привязать к веревке, к которой привязать еще один такой же, но с более длинной нитью. При этом длина нитки второго маятника может регулироваться. Если привести в движение оба маятника, а длину второй нитки постепенно изменять, то можно будет заметить, что амплитуда увеличивается по мере приближения размеров обеих ниток.

В этом случае первый маятник будет приемником колебаний, а второй — передатчиком. Причиной увеличения амплитуды является колебание подвески с такой же частотой.

Примеры

Свет

Основные статьи: Свет и Электромагнитное излучение

Полный спектр электромагнитное излучение с выделенной видимой частью

Видимый свет — это электромагнитная волна, состоящий из колеблющихся электрический и магнитные поля путешествовать в космосе. Частота волны определяет ее цвет: 4×1014 красный свет, 8×1014 Гц фиолетовый свет, а между ними (в диапазоне 4-8×1014 Гц) все остальные цвета видимый спектр. Электромагнитная волна может иметь частоту меньше 4×1014 Гц, но он будет невидим для человеческого глаза; такие волны называются инфракрасный (ИК) излучение. На еще более низкой частоте волна называется микроволновая печь, а на еще более низких частотах он называется радиоволна. Точно так же электромагнитная волна может иметь частоту выше, чем 8×1014 Гц, но он будет невидим для человеческого глаза; такие волны называются ультрафиолетовый (УФ) излучение. Даже более высокочастотные волны называются Рентгеновские лучи, а еще выше гамма излучение.

Все эти волны, от радиоволн самой низкой частоты до гамма-лучей самой высокой частоты, в основном одинаковы, и все они называются электромагнитное излучение. Все они движутся в вакууме с одинаковой скоростью ( скорость света), давая им длины волн обратно пропорционально их частотам.

c = ж λ {displaystyle displaystyle c = flambda}

куда c

это скорость света ( в вакууме или меньше в других средах),
ж
— частота, λ — длина волны.

В дисперсионные средыНапример, у стекла скорость зависит от частоты, поэтому длина волны не совсем обратно пропорциональна частоте.

Звук

Основная статья: Частота звука

В звуковая волна спектр, с приблизительным указанием некоторых приложений

Звук распространяется как механические колебательные волны давления и смещения в воздухе или других веществах.[5] В целом частотные составляющие звука определяют его «цвет», его тембр. Говоря о частоте (в единственном числе) звук, это означает свойство, которое больше всего определяет подача.[6]

Частоты, которые может слышать ухо, ограничены конкретный диапазон частот. В слышимая частота диапазон для людей обычно составляет примерно 20 и 20 000 Гц (20 кГц), хотя предел высокой частоты обычно снижается с возрастом. Другой разновидность имеют разный диапазон слышимости. Например, некоторые породы собак могут воспринимать вибрации до 60 000 Гц.[7]

Во многих СМИ, например в эфире, скорость звука примерно не зависит от частоты, поэтому длина звуковой волны (расстояние между повторениями) примерно обратно пропорциональна частоте.

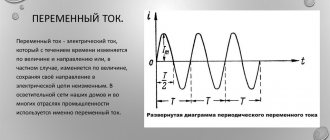
Линейный ток

Основная статья: Частота коммунальных услуг

В Европа, Африка, Австралия, Южный Южная Америка, большинство Азия, и Россия, частота переменный ток в бытовые электрические розетки составляет 50 Гц (близка к тон G), а в Северная Америка и северный Южная Америка, частота переменного тока в бытовых электрических розетках 60 Гц (между тона B ♭ и B; это второстепенная треть выше европейской частоты). Частота ‘гудеть’в Аудио запись может показать, где была сделана запись, в странах, использующих европейскую или американскую частоту сети.

Колебательный контур

Является еще одним примером колебаний, на котором основаны все радиоприемники. Контур играет роль приемника сигнала.

В простейшем примере представляет собой замкнутую цепь из катушки индуктивности и конденсатора. При определенных обстоятельствах в подобном контуре могут возникать и поддерживаться электрические колебания.

Для возбуждения колебаний необходимо подключить источник постоянного напряжения к конденсатору и зарядить его. После этого источник убрать, а цепь замкнуть.

Конденсатор разряжается через катушку индуктивности, а в цепи создается ток, интенсивность которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.

Электрический заряд конденсатора преобразовался в магнитное поле. После этого магнитное поле катушки будет уменьшаться, а конденсатор обратно заряжаться. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: частотой, амплитудой и периодом.

Они являются свободными и затухающими. Чтобы их поддерживать, необходимо периодически заряжать конденсатор.

Смотрите также

Смотрите также: Частота (значения) и Категория: Единицы частоты

Апериодическая частота
Частота звука
Полоса пропускания (обработка сигнала)
Частота среза
Даунсэмплинг
Электронный фильтр
Диапазон частот
Преобразователь частоты
Частотный диапазон
Распределение частоты
Расширитель частоты
Сетка частот
Модуляция частоты
Частотный спектр
Частота взаимодействия
Собственная частота
Отрицательная частота
Периодичность (значения)
Розовый шум
Преселектор
Характеристики радиолокационного сигнала
Сигнализация (телекоммуникации)
Расширенный спектр
Спектральная составляющая
Трансвертер
Передискретизация

Метрологические аспекты

Частота колебаний нашла своё применение даже в метрологии. Различные устройства имеют много функций:

Измеряют частоту импульсов. Они представлены электронно-счётными и конденсаторными типами.
Определяют частоту спектральных составляющих. Существуют гетеродинные и резонансные типы.
Производят анализ спектра.
Воспроизводят необходимую частоту с заданной точностью. При этом могут применяться различные меры: стандарты, синтезаторы, генераторы сигналов и другая техника этого направления.
Сравнивают показатели полученных колебаний, в этих целях используют компаратор или осциллограф.

Линейная скорость

Определение линейной скорости относится к разделу физики о механике и подразделу о кинематике в рамках вопроса движения по окружности. В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.

Дадим определение линейной скорости.

Линейная скорость $V$ — это физическая величина, показывающая путь, который прошло тело за единицу времени.

Формула линейной скорости:

$V=frac$, где $S$ — путь, $t$ — время, за которое точка прошла путь $S$.

Также существует иной вариант этой формулы:

$V=frac$, где $l$ — путь, $t$ — время, за которое точка прошла по дуге $l$.

В некоторых учебниках линейная скорость также обозначается маленькой буквой $v$.

Есть ещё одна формула, по которой можно найти линейную скорость:

$2pi$ соответствует полной окружности (360 угловым градусам).

$vec V$ направленена по касательной к тракетории.

Частота колебаний — определение, формулы и характеристики