| Угловая частота | |
| ω | |
| Размерность | T −1 |
| Единицы измерения | |
| СИ | рад/с |
| СГС | рад/с |
| Другие единицы | градус/с |
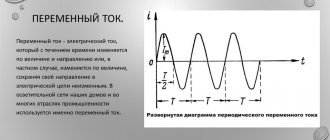
Углова́я частота́
(синонимы: радиальная частота, циклическая частота, круговая частота, частота вращения) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В Международной системе единиц (СИ) и системе СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны).
Угловая частота является производной по времени от фазы колебания:
ω = ∂ φ / ∂ t .
Другое распространённое обозначение ω = φ ˙ . >.>
Угловая частота связана с частотой ν соотношением [1]
ω = 2 π ν . u >.>
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
ω = 360 ∘ ν . u >.>
В случае вращательного движения угловая частота численно равна углу, на который повернется вращающееся тело за единицу времени (то есть равна модулю вектора угловой скорости), в случае колебательного движения — приращению полной фазы колебания за единицу времени. Численно угловая (циклическая) частота равна числу циклов (колебаний, оборотов) за 2 π единиц времени.
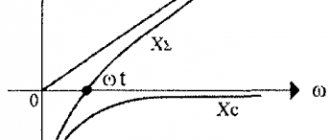
Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC
-контура равна ω L C = 1 / L C , =1/>,> тогда как обычная резонансная частота ν L C = 1 / ( 2 π L C ) . u _=1/(2pi >).>
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что переводные множители 2 π и 1/(2 π ), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
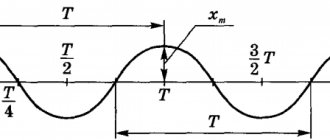
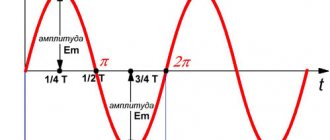
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
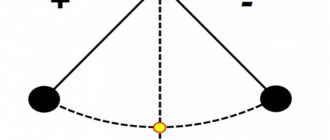
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:
.
В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:
.
Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Частные случаи формул для вычисления циклической частоты
Груз на пружине (пружинный маятник — идеальная модель) совершает гармонические колебания с круговой частотой равной:
$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.
Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.
Примером физического маятника является математический маятник. Круговая частота его колебаний равна:
Угловая частота затухающих колебаний находится как:
где $\delta $ — коэффициент затухания; в случае с затуханием колебаний $_0$ называют собственной угловой частотой колебаний.
Примеры движения
Колебательное движение является одним из наиболее распространенных в природе. Например, можно представить себе струны музыкальных инструментов, качели или голосовые связки человека.
В физике колебаниями называются процессы, которые повторяются через равные промежутки времени. Подобные движения рассматривается посредством нескольких моделей:
- тела, подвешенного на пружине (двигающееся по направлению вверх-вниз);
- груза на нитке;
- электрического контура и других.
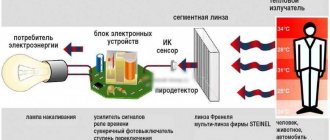
Звук
Звук – это колебания упругой среды, воспринимаемые органом слуха.
Условия, необходимые для возникновения и ощущения звука:
- наличие источника звука;
- наличие упругой среды между источником и приемником звука;
- наличие приемника звука; • частота колебаний должна лежать в звуковом диапазоне;
- мощность звука должна быть достаточной для восприятия.
Звуковые волны – это упругие волны, вызывающие у человека ощущение звука, представляющие собой зоны сжатия и разряжения, передающиеся на расстояние с течением времени.
Классификация звуковых волн:
- инфразвук (\( \nu \) < 16 Гц);
- звуковой диапазон (16 Гц < \( \nu \) < 20 000 Гц);
- ультразвук (\( \nu \) > 20 000 Гц).
Скорость звука – это скорость распространения фазы колебания, т. е. области сжатия и разряжения среды.
Скорость звука зависит
- от упругих свойств среды:
в воздухе – 331 м/с, в воде – 1400 м/с, в металле – 5000 м/с;
- от температуры среды:
в воздухе при температуре 0°С – 331 м/с, в воздухе при температуре +15°С – 340 м/с.
Характеристики звуковой волны
- Громкость – это величина, характеризующая слуховые ощущения человека, зависящая от амплитуды колебаний в звуковой волне. Единицы измерения – дБ (децибел).
- Высота тона – это величина, характеризующая слуховые ощущения человека, зависящая от частоты колебаний в звуковой волне. Чем больше частота, тем выше звук. Чем меньше частота, тем ниже звук.
- Тембр – это окраска звука.
Музыкальный звук – это звук, издаваемый гармонически колеблющимся телом. Каждому музыкальному тону соответствует определенная длина и частота звуковой волны. Шум – хаотическая смесь тонов.
Амплитуда, период и частота
Если подвесить одновременно два груза на две разные нити и запустить их, то можно заметить, что расстояние отклонения груза от среднего положения до крайнего — разное.
Это величина носит название амплитуды. Обозначается буквой А и измеряется в системе Си в метрах. Также для обозначения подобного движения применяются следующие термины:
- Время, за которое маятник приходит в одно и то же положение, называется периодом колебаний.
- Количество колебаний в единицу времени представляет собой частоту. Она измеряется в Герцах (Гц). Имеет обратную зависимость от периода.
- Циклическая частота колебаний (угловая, круговая) представляет собой количество колебаний за 2 π секунд. Обозначается греческой буквой омега. Она вводится для упрощения расчетов в теоретической физике и электронике. Единица измерения циклической частоты рад/с.
- Если имеется два графика функций с одинаковой частотой, но сдвинуты относительно друг друга, то различна их фаза колебаний.
Ссылки и примечания [ править ]
- ^ a b Каммингс, Карен; Холлидей, Дэвид (2007). Понимание физики . Нью-Дели: John Wiley & Sons Inc., авторизованная перепечатка для Wiley — Индия. стр. 449, 484, 485, 487. ISBN 978-81-265-0882-2.(UP1)
- Holzner, Стивен (2006). Физика для чайников . Хобокен, Нью-Джерси: Wiley Publishing Inc., стр.201 . ISBN 978-0-7645-5433-9. угловая частота.
- Лернер, Лоуренс С. (1996-01-01). Физика для ученых и инженеров . п. 145. ISBN 978-0-86720-479-7.
- Мор, JC; Филлипс, WD (2015). «Безразмерные единицы в СИ». Метрология
.
52
(1): 40–47. arXiv : 1409.2794 . Bibcode : 2015Metro..52 … 40M . DOI : 10.1088 / 0026-1394 / 52/1/40 . S2CID 3328342 . - Перейти
↑ Mills, IM (2016). «В единицах радиан и цикл для угла плоскости величины».
Метрология
.
53
(3): 991–997. Bibcode : 2016Metro..53..991M . DOI : 10.1088 / 0026-1394 / 53/3/991 . - «Единицы СИ необходимо реформировать, чтобы избежать путаницы» . От редакции. Природа
.
548
(7666): 135. 7 августа 2011 г. doi : 10.1038 / 548135b . PMID 28796224 . - PR Бункер; IM Mills; Пер Дженсен (2019). «Постоянная Планка и ее единицы». J Quant Spectrosc Radiat Transfer
.
237
: 106594. дои : 10.1016 / j.jqsrt.2019.106594 . - PR Бункер; Пер Дженсен (2020). «Постоянная Планка действия А ». J Quant Spectrosc Radiat Transfer
.
243
: 106835. дои : 10.1016 / j.jqsrt.2020.106835 . h {\displaystyle h} - Serway, Raymond A .; Джуэтт, Джон В. (2006). Основы физики (4-е изд.). Белмонт, Калифорния: Brooks / Cole — Thomson Learning. стр. 375, 376, 385, 397. ISBN 978-0-534-46479-0.
- Нахви, Махмуд; Эдминистер, Джозеф (2003). Очерк теории и проблем электрических цепей Шаума . Компании МакГроу-Хилл (McGraw-Hill Professional). стр. 214, 216. ISBN 0-07-139307-2.(LC1)
Связанное чтение:
- Оленик, Ричард П .; Апостол, Том М .; Гудштейн, Дэвид Л. (2007). Механическая Вселенная . Нью-Йорк: Издательство Кембриджского университета. С. 383–385, 391–395. ISBN 978-0-521-71592-8.
Математический маятник
Эта модель рассматривает движение груза, подвешенного на нитке. Описывается система, в которой масса нитки намного меньше массы груза, а ее длина намного больше его размеров.
Также нить должна быть невесомой и нерастяжимой.
Груз в этом случае считается материальной точкой.
При выполнении этих условий частота колебаний маятника и период не будут зависеть от массы груза. Движение математического маятника рассматривается при небольшом угле отклонения (α). Последний измеряется в радианах, поэтому приблизительно соответствует по значению его синусу и тангенсу. Этот же угол пропорционален отношению смещения на длину нити:
α=x/l.
На маятник действует синусовая составляющая силы тяжести и тангенсовая сила натяжения нити. Согласно второму закону Ньютона: ma=-mgsin (α). Откуда можно получить a=-gx/l
Вторая производная уравнения движения дает a=-(ω)^2x
Таким образом: -gx/l=-(ω)^2x -> ω ^2=g/l.
Период: T=2π /ω T=2π*sqrt (g/l)
Это формула Галилея, которая описывает движение математического маятника.
Формула частоты колебаний для математического маятника: v=sqrt (l/g)/2π.
Резонанс
Резонанс – явление резкого возрастания амплитуды колебаний, которое происходит при совпадении частоты вынуждающей силы и собственной частоты колебаний тела.
Условие резонанса:
\( v_0 \) – собственная частота колебаний маятника.
На рисунке изображены резонансные кривые для сред с разным трением. Чем меньше трение, тем выше и острее резонансная кривая.
Явление резонанса учитывается при периодически изменяющихся нагрузках в машинах и различных сооружениях. Также резонанс используется в акустике, радиотехнике и т. д.
Пружинный маятник
Подобным термином называется система, в которой движения совершает груз, подвешенный на легкой пружине.
Тело находится в положении равновесия, если пружина не деформирована. Если ее растянуть или сжать, то система начнет колебания под действием силы упругости, которая направлена на приведение маятника в положение равновесия.
Сила упругости пропорциональна смещению тела (x), но направлена противоположно. Коэффициент пропорциональности между этими двумя величинами носит название жесткости пружины (k). Таким образом:
F=-kx.
Сила упругости достигает наибольшей величины в положении максимального отклонения тела (амплитуда, смещение) от равновесия. В этой точке наибольшую величину имеет и ускорение.
По мере того, как тело приближается к положению равновесия, уменьшается сила упругости и ускорение. В средней точки обе величины равны нулю, но ненулевое значение имеет скорость тела. Поэтому груз не останавливается, а продолжает движение.
После прохождения положения равновесия он двигается в обратном направлении по инерции, а сила упругости тянет его назад. Благодаря трению воздуха скорость уменьшается, и маятник останавливается.
Все эти модели можно отнести к классическому гармоническому осциллятору — системе, которая имеет одну степень свободы и описывается единственным уравнением.
Примеры [ править ]
Круговое движение [ править ]
Основная статья: Круговое движение
Во вращающемся или орбитальном объекте, существует зависимость между расстоянием от оси, , тангенциальная скорость , и угловая частота вращения. За один период тело, совершая круговое движение, преодолевает расстояние . Это расстояние также равна окружности пути , проходимый телом, . Уравнивая эти две величины и вспоминая связь между периодом и угловой частотой, получаем: р {\ displaystyle r} v {\ displaystyle v} Т {\ displaystyle T} v Т {\ displaystyle vT} 2 π р {\ displaystyle 2 \ pi r} ω знак равно v / р . {\ displaystyle \ omega = v / r.}
Колебания пружины [ править ]
| Часть серии по |
| Классическая механика |
| F знак равно d d т ( м v ) {\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})} Второй закон движения |
|
ветви
|
Основы
|
Составы
|
Основные темы
|
Вращение
|
Ученые
|
| Категории ► Классическая механика |
|
Предмет, прикрепленный к пружине, может колебаться . Если предположить, что пружина идеальная и безмассовая без демпфирования, то движение будет простым и гармоничным с угловой частотой, задаваемой [9]
ω = k m , {\displaystyle \omega ={\sqrt {\frac {k}{m}}},}
куда
k
— жесткость пружины ,
m
— масса объекта.
ω называется собственной частотой (которую иногда можно обозначать как ω 0 ).
Когда объект колеблется, его ускорение можно рассчитать по формуле
a = − ω 2 x , {\displaystyle a=-\omega ^{2}x,}
где x
— смещение из положения равновесия.
Используя «обычную» частоту оборотов в секунду, это уравнение будет
a = − 4 π 2 f 2 x . {\displaystyle a=-4\pi ^{2}f^{2}x.}
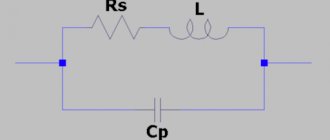
LC схемы [ править ]
Резонансная угловая частота в последовательном LC-контуре равна квадратному корню из обратной величины произведения емкости ( C,
измеренной в фарадах ) и индуктивности контура (
L
, в единицах СИ — генри ): [10]
ω = 1 L C . {\displaystyle \omega ={\sqrt {\frac {1}{LC}}}.}
Добавление последовательного сопротивления (например, из-за сопротивления провода в катушке) не изменяет резонансную частоту последовательного LC-контура. Для параллельной настроенной схемы приведенное выше уравнение часто является полезным приближением, но резонансная частота действительно зависит от потерь в параллельных элементах.
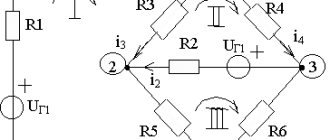
Колебательный контур
Является еще одним примером колебаний, на котором основаны все радиоприемники. Контур играет роль приемника сигнала.
В простейшем примере представляет собой замкнутую цепь из катушки индуктивности и конденсатора. При определенных обстоятельствах в подобном контуре могут возникать и поддерживаться электрические колебания.
Для возбуждения колебаний необходимо подключить источник постоянного напряжения к конденсатору и зарядить его. После этого источник убрать, а цепь замкнуть.
Конденсатор разряжается через катушку индуктивности, а в цепи создается ток, интенсивность которого увеличивается по мере разряда конденсатора. Вокруг катушки создается магнитное поле.
Электрический заряд конденсатора преобразовался в магнитное поле. После этого магнитное поле катушки будет уменьшаться, а конденсатор обратно заряжаться. Процесс повторяется циклически и описывается теми же характеристиками, что и механические колебания: частотой, амплитудой и периодом.
Они являются свободными и затухающими. Чтобы их поддерживать, необходимо периодически заряжать конденсатор.
Длина волны
Длина волны – это расстояние, на которое волна распространяется за один период, т. е. это кратчайшее расстояние между двумя точками среды, колеблющимися в одинаковых фазах. Обозначение – \( \lambda \), единицы измерения – м.
Расстояние между соседними гребнями или впадинами в поперечной волне и между соседними сгущениями или разряжениями в продольной волне равно длине волны.
Скорость распространения волны – это скорость перемещения горбов и впадин в поперечной волне и сгущений или разряжений в продольной волне.