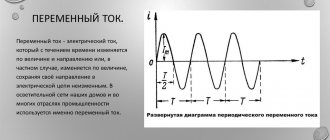
Oscillation frequency - definition, formulas and characteristics

Number of repetitions or cycles per unit time

For other uses, see Frequency (disambiguation).

"Frequencies" redirects here. For the film, see Frequencies (film). For the album, see Frequencies (album).

For more coverage of this topic, see Temporary Rate.

Frequency
Common symbols	f , ν
SI unit
B SI Base Units	−1
Measurement	T − 1 {displaystyle {mathsf {T}}^{- 1}}

Frequency

number of times a repeating event occurs per unit of time.[1]
It is also called temporal frequency
, which emphasizes the contrast between spatial frequency and angular frequency.
Frequency is measured in units of hertz (Hz), which corresponds to one repetition of an event per second. A period
is the duration of one cycle in a repeating event, so a period is a reciprocal frequency.[2]
For example: if the heart of a newborn baby beats at a frequency of 120 times per minute (2 hertz), its period, T
, - the time interval between beats - is half a second (60 seconds divided by 120 beats). Frequency is an important parameter used in science and technology to determine the speed of oscillatory and vibrating phenomena such as mechanical vibrations, audio signals (sound), radio waves, and light.

Definitions

These three dots flash, or cycle
, periodically - from the lowest frequency (0.5 Hz) to the highest frequency (2.0 Hz), from top to bottom.
For each flashing dot: "f" is the frequency in Hertz, (Hz) - or the number of events per second (cycles per second) that the dot is flashing; while “T” is the period
, or
time
, in seconds (s) of each cycle (the number of seconds per cycle). Note T and shipping costs are mutually valuable to each other. As time passes - here, moving from left to right along a horizontal axis - the five sine waves change or change, regularly at different rates. The red wave (top) has the lowest frequency (slowest speed cycles) and the purple wave (bottom) has the highest frequency (fastest speed cycles).

For cyclic processes, such as rotation, oscillations, or waves, frequency is defined as the number of cycles per unit time. In physics and engineering disciplines such as optics, acoustics, and radio, frequency is usually denoted by the Latin letter f

or the Greek letter
ν {displaystyle u}
or
ν
(nu) (see, for example, Planck's Formula).

The relationship between the frequency and period, T{displaystyle T}, of a repeating event or oscillation is given by

f = 1 T. {displaystyle f = {frac {1} {T}}.}

Movement examples

Oscillatory motion is one of the most common in nature. For example, you can imagine the strings of a musical instrument, a swing, or a person's vocal cords.

In physics, oscillations are processes that repeat at regular intervals. Such movements are considered through several models:

a body suspended on a spring (moving up and down);
weight on a string;
electrical circuit and others.

Units

The derived SI unit of frequency is the hertz (Hz), named after the German physicist Heinrich Hertz. One hertz means that the event is repeated once every second. If the TV refresh rate is 1 hertz, the TV screen will change (or refresh) the image once per second. The previous name for this division was cycles per second (cps). In unit per period - second.

The traditional unit of measurement for rotating mechanical devices is revolutions per minute, abbreviated rpm or rpm. 60 revolutions per minute equals one hertz.[3]

Amplitude and phase of oscillations

The amplitude of oscillations is the modulus of the greatest displacement of the body from the equilibrium position. Designation – $ A\, (X_{max}) $, units of measurement – m.

The oscillation phase is a quantity that determines the state of the oscillatory system at any time. Designation – $ \varphi $, units of measurement – rad (radian).

The oscillation phase is a quantity under the sine or cosine sign. It shows how much of the period has passed since the beginning of the oscillations. The phase of harmonic oscillations changes during the oscillation process. $ \varphi_0 $ – initial phase of oscillations. The initial phase of oscillations is a value that determines the position of the body at the initial moment of time.

Important! The path traveled by a body in one complete oscillation is equal to four amplitudes.

Period vs Frequency

For convenience, long and slow waves, such as ocean surface waves, are typically described by wave period rather than frequency. Short and fast waves, like audio and radio, are usually described by their frequency rather than their period. These commonly used transformations are listed below:

Frequency	1 MHz (10−3 Hz)	1 Hz (100 Hz)	1 kHz (103 Hz)	1 MHz (106 Hz)	1 GHz (109 Hz)	1 THz (1012 Hz)
Period	1 x (103 s)	1 s (100 s)	1 ms (10−3 s)	1 µs (10−6 s)	1 ns (10−9 s)	1 PC. (10−12 s)

Content

1 Definitions and units
2 Period vs frequency
3 Related frequency types
4 When waves propagate
5 Measurement 5.1 Counting
5.2 Strobe
5.3 Frequency meter
5.4 Heterodyne methods

6 Examples

6.1 Light

6.2 Sound

6.3 Line current

7 Aperiodic frequency

8 See also

9 Notes

10 Links

11 Sources

12 Further reading

13 External links

Related Frequency Types

For other uses, see Frequency (disambiguation).

Diagram of the relationship between different types of frequency and other properties of waves.

Angular frequency, usually denoted by the Greek letter ω (omega), is defined as the rate of change of angular displacement, θ
, (during rotation), or the rate of change of phase of a sinusoidal waveform (especially in oscillations and waves), or as the rate of change of argument to a function sine:

y ( t ) = sin ⁡ ( θ ( t ) ) = sin ⁡ ( ω t ) = sin ⁡ ( 2 π f t ) {displaystyle y (t) = sin left (heta (t) ight) = sin (omega t ) = sin (2mathrm {pi} ft)} d θ d t = ω = 2 π f {displaystyle {frac {mathrm {d} heta} {mathrm {d} t}} = omega = 2mathrm {pi} f} Angular frequency is usually measured in radians per second (rad/s), but for discrete-time signals, it can also be expressed in radians per sample interval, which is a dimensionless quantity. The angular frequency (in radians) is 2π times greater than the normal frequency (in Hz).

Spatial frequency is similar to temporal frequency, but the time axis is replaced by one or more spatial displacement axes. For example.:

y ( t ) = sin ⁡ ( θ ( t , x ) ) = sin ⁡ ( ω t + k x ) { displaystyle y ( t ) = sin left ( heta ( t , x ) ight) = sin ( omega t + kx )} d θ d x = k {displaystyle {frac {mathrm {d} heta} {mathrm {d} x}} = k} The wave number, k
, is the spatial frequency analogue of angular time frequency and is measured in radians per meter. In the case of more than one spatial dimension, the wave number is a vector number.

Speed concept

When we compare the movement of any bodies, we say that some bodies move faster, while others move slower. We use such simple terminology in everyday life, talking, for example, about traffic. In physics, the speed of movement of bodies is characterized by a certain value. This quantity is called speed. General definition of speed (if the body is moving uniformly):

Velocity during uniform motion of a body is a physical quantity that shows how far the body has traveled per unit time.

By uniform motion of a body it is meant that the speed of the body is constant. The formula for finding speed: $v=frac$, $s$ is the path traveled by the body (that is, the length of the line), $t$ is the time (that is, the period of time during which the path was traveled).

According to the international SI system, the unit of linear speed is derived from two basic units - the meter and the second, that is, it is measured in meters per second (m/s). This means that the unit of speed is the speed of such uniform motion that a body travels a distance of one meter in one second.

Try asking your teachers for help

Speed is also often measured in km/h, km/s, cm/s.

Let's look at a simple example of a speed calculation problem.

Task. Moving uniformly, the train covers 219 km in 4 hours. Find its speed of movement.

Solution. $v=frac<219 km><4 h>=54.75frac<km><h>$. Let's convert kilometers into meters and hours into seconds: $54.75frac<km><h>=frac<54750 m><3600c>approx 15.2frac<m>$.

From the example we see that the numerical value of the speed differs depending on the selected unit of measurement.

In addition to the numerical value, speed has a direction. The numerical value of a quantity in physics is called the modulus. When a physical quantity also has a direction, then this quantity is called a vector quantity. That is, speed is a vector physical quantity.

In writing, the velocity module is denoted by $v$, and the velocity vector by $vec v$.

In turn, such quantities as path, time, length and others are characterized only by a numerical value. Then they say that these are scalar physical quantities.

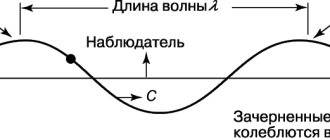
When waves propagate

Further information: Wave propagation

For periodic waves in non-disperse media (that is, a medium in which the wave speed does not depend on frequency), frequency has an inverse relationship with wavelength, λ

(lambda).
Even in dispersive media, the frequency w
of a sine wave is equal to the phase velocity
v
of the wave divided by the wavelength
λ
of the wave:
w = v λ.
{displaystyle f = {frac {v} {lambda}}.} to the special case of electromagnetic waves moving through a vacuum, then v = c

, where
c
is the speed of light in vacuum, and this expression becomes:
x = c λ.
{displaystyle f = {frac {c} {lambda}}.} When waves from monochrome travel from one to the other, their frequency remains the same—only their wavelength and speed change.

Spring pendulum

A similar term refers to a system in which movement is performed by a load suspended on a light spring.

The body is in equilibrium if the spring is not deformed. If it is stretched or compressed, the system will begin to oscillate under the action of an elastic force, which is aimed at bringing the pendulum to an equilibrium position.

The elastic force is proportional to the displacement of the body (x), but is directed in the opposite direction. The proportionality coefficient between these two quantities is called the spring stiffness (k). Thus:

F=-kx.

The elastic force reaches its greatest value in the position of maximum deviation of the body (amplitude, displacement) from equilibrium. At this point the acceleration is greatest.

As the body approaches the equilibrium position, the elastic force and acceleration decrease. At the midpoint, both quantities are equal to zero , but the speed of the body has a non-zero value. Therefore, the load does not stop, but continues to move.

After passing the equilibrium position, it moves in the opposite direction by inertia, and the elastic force pulls it back. Due to air friction, the speed decreases and the pendulum stops.

All these models can be classified as a classical harmonic oscillator - a system that has one degree of freedom and is described by a single equation.

Measurement

Count

Calculating the frequency of a recurring event is done by counting the number of times that event occurs during a given period of time and then dividing that number by the length of the time period. For example, if 71 events occurred within 15 seconds, the frequency would be:

f = 71 15 s ≈ 4.73 Hz {displaystyle f = {frac {71} {15, {ext {s}}}} approximately 4.73, {ext {Hz}}}

Unless the number of samples is very large, it is more accurate to measure the time interval for a predetermined number of occurrences than the number of repetitions within a certain time.[4] The last method introduces a random error into the count from zero to one, etc. for an average half count. This is called a gating error.

and causes an average error in the calculated frequency Δ f = 1 2 T m {displaystyle Delta f = {frac {1} {2T_{m}}}} , or a fractional error Δ f f = 1 2 f T m {displaystyle {frac { Delta f} {f}} = {frac {1} {2fT_ {m}}}} where T {displaystyle T} is the time interval and f {displaystyle f} is the measured frequency.
This error decreases with frequency, so the problem usually occurs at low frequencies when the number of samples N
is small.

Resonant reed frequency meter, an obsolete device that was used from about 1900 to the 1940s to measure the frequency of alternating current. It consists of a strip of metal with reeds of different lengths that are vibrated by an electromagnet. When an unknown frequency is applied to an electromagnet, a reed resonant at that frequency will vibrate with a large amplitude visible next to the scale.

Strobe

An older method of measuring the rotational speed or vibration of objects is to use a strobe light. This is an intense, periodically flashing light (flasher) whose frequency can be adjusted using a calibrated timing circuit. The strobe is aimed at a rotating object, and the frequency is adjusted up and down. When the strobe frequency is equal to the frequency of a rotating or vibrating object, the object completes one cycle of oscillation and returns to its original position between flashes of light, so when illuminated by a strobe light, the object appears motionless. The frequency can then be read from the calibrated readings on the strobe light. The downside to this method is that an object rotating at an integer multiple of the strobe frequency will also appear stationary.

Frequency meter

Main article: Frequency meter

Modern frequency meter

Higher frequencies are usually measured using a frequency meter. This is an electronic instrument that measures the frequency of applied repetitive electronic signals and displays the result in Hertz on a digital display. It uses digital logic to count the number of cycles within a time interval set by a precision quartz time base. Cyclic processes that are not electrical, such as shaft speed, mechanical vibrations or sound waves, can be converted into a repeating electronic signal using a transducer and the signal is fed to a frequency meter. As of 2022, frequency counters can cover a range of up to approximately 100 GHz. This represents the limit of direct counting methods; frequencies above this must be measured by indirect methods.

Heterodyne methods

Outside the range of frequency meters, frequencies of electromagnetic signals are often measured indirectly using heterodyning (frequency conversion). A reference signal of a known frequency close to an unknown one is mixed with the unknown frequency in a nonlinear mixing device such as a diode. This creates a local oscillator or "beat" signal based on the difference between the two frequencies. If the two signals are close in frequency, the local oscillator is low enough to be measured with a frequency counter. This process only measures the difference between the unknown frequency and the reference frequency. Multiple stages of heterodyning can be used to achieve higher frequencies. Current research is extending this method to infrared and light frequencies (optical heterodyne detection).

Resonance phenomenon

This concept is of particular importance for describing oscillations. If there is some influence, the frequency of which approaches the natural frequency of the system, then the latter reacts with a sharp increase in amplitude.

The phenomenon of resonance can be imagined using the example of the same mathematical pendulum. To do this, you need to tie the pendulum to a rope, to which you tie another similar one, but with a longer thread. In this case, the length of the thread of the second pendulum can be adjusted. If you set both pendulums in motion and gradually change the length of the second thread, you will notice that the amplitude increases as the size of both threads approaches.

In this case, the first pendulum will be a receiver of oscillations, and the second will be a transmitter. The reason for the increase in amplitude is the vibration of the suspension at the same frequency.

Examples

Light

Main articles: Light and Electromagnetic radiation

Full spectrum electromagnetic radiation with a highlighted visible part

Visible light is an electromagnetic wave made up of oscillating electric and magnetic fields traveling through space. The frequency of the wave determines its color: 4×1014 red light, 8×1014 Hz violet light, and between them (in the range of 4-8×1014 Hz) all other colors of the visible spectrum. An electromagnetic wave may have a frequency less than 4×1014 Hz, but it will be invisible to the human eye; Such waves are called infrared (IR) radiation. At an even lower frequency the wave is called a microwave, and at even lower frequencies it is called a radio wave. Likewise, an electromagnetic wave may have a frequency higher than 8x1014 Hz, but it will be invisible to the human eye; Such waves are called ultraviolet (UV) radiation. Even higher frequency waves are called X-rays, and even higher ones are called gamma radiation.

All of these waves, from radio waves of the lowest frequency to gamma rays of the highest frequency, are basically the same, and they are all called electromagnetic radiation. They all move in a vacuum at the same speed (the speed of light), giving them wavelengths inversely proportional to their frequencies.

c = f λ {displaystyle displaystyle c = flambda}

where c

this is the speed of light (in a vacuum or less in other media),
w
is the frequency, λ is the wavelength.

In dispersive media, for example, in glass, the speed depends on the frequency, so the wavelength is not exactly inversely proportional to the frequency.

Sound

Main article: Sound frequency

The sound wave spectrum, with approximate indications of some applications

Sound travels as mechanical vibrational waves of pressure and displacement in air or other substances.[5] In general, the frequency components of a sound determine its “color”, its timbre. When we talk about frequency (singular) of a sound, it means the property that most determines pitch.[6]

The frequencies that the ear can hear are limited to a specific frequency range. The audible frequency range for humans is typically between about 20 and 20,000 Hz (20 kHz), although the high frequency limit generally decreases with age. Another variety has a different range of audibility. For example, some dog breeds can perceive vibrations up to 60,000 Hz.[7]

In many media, such as broadcasting, the speed of sound is approximately independent of frequency, so the length of the sound wave (the distance between repetitions) is approximately inversely proportional to frequency.

Line current

Main article: Utility frequency

In Europe, Africa, Australia, Southern South America, most of Asia, and Russia, the frequency of AC current in household electrical outlets is 50 Hz (close to tone G), and in North America and northern South America, the frequency of AC current in household electrical outlets 60 Hz (between the tones B♭ and B; this is a minor third above the European frequency). The frequency of the 'beep' in an Audio recording can indicate where the recording was made, in countries using a European or US network frequency.

Oscillatory circuit

Is another example of the oscillation on which all radios are based. The circuit plays the role of a signal receiver.

In the simplest example, it is a closed circuit of an inductor and a capacitor. Under certain circumstances, electrical oscillations can occur and be maintained in such a circuit.

To excite oscillations, it is necessary to connect a constant voltage source to the capacitor and charge it. After this, remove the source and close the circuit.

The capacitor is discharged through the inductor, and a current is created in the circuit, the intensity of which increases as the capacitor is discharged. A magnetic field is created around the coil.

The electrical charge of the capacitor was converted into a magnetic field. After this, the magnetic field of the coil will decrease, and the capacitor will be charged back. The process is repeated cyclically and is described by the same characteristics as mechanical vibrations: frequency, amplitude and period.

They are free and damping. To maintain them, it is necessary to periodically charge the capacitor .

Metrological aspects

Oscillation frequency has found its application even in metrology. Different devices have many functions:

The pulse frequency is measured. They are represented by electronic counting and capacitor types.
The frequency of spectral components is determined. There are heterodyne and resonant types.
Spectrum analysis is carried out.
Reproduce the required frequency with a given accuracy. In this case, various measures can be used: standards, synthesizers, signal generators and other techniques in this direction.
The indicators of the obtained oscillations are compared; for this purpose, a comparator or oscilloscope is used.

Recommendations

"Determination of FREQUENCY". Retrieved October 3, 2016.
"Definition of PERIOD". Retrieved October 3, 2016.
Davis, A. (1997). Handbook of Condition Monitoring: Techniques and Methodology
. New York: Springer. ISBN 978-0-412-61320-3.
Bakshi, K. A.; AVERAGE. Bakshi; U.A. Bakshi (2008). Electronic measuring systems
. USA: Technical Publications. pp. 4–14. ISBN 978-81-8431-206-5.
"Definition of SOUND". Retrieved October 3, 2016.
Pilhofer, Michael (2007). Music Theory for Dummies
. For Dummies. paragraph 97. ISBN 9780470167946.
Ehlert, Glenn; Timothy Condon (2003). "Frequency Range of Canine Hearing." Handbook of Physics. Retrieved 2008-10-22.

Linear speed

The definition of linear speed refers to the section of physics on mechanics and the subsection on kinematics within the framework of the issue of circular motion. In measuring the speed of movement along a circle, angular speed and linear speed are distinguished.

Let's define linear speed.

Linear velocity $V$ is a physical quantity that shows the path a body has traveled per unit time.

Linear speed formula:

$V=frac$, where $S$ is the path, $t$ is the time during which the point traveled the path $S$.

There is also another version of this formula:

$V=frac$, where $l$ is the path, $t$ is the time during which the point passed along the arc $l$.

In some textbooks, linear velocity is also denoted by the small letter $v$.

There is another formula by which you can find linear speed:

$2pi$ corresponds to a complete circle (360 angular degrees).

$vec V$ is directed tangentially to the trajectory.