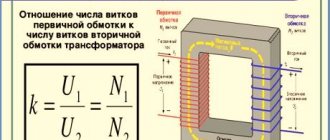
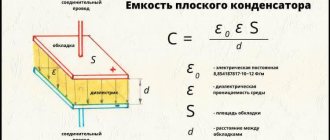
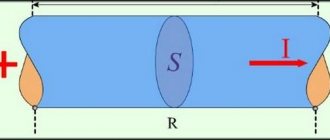
В радиотехнике часто приходится сталкиваться с индуктивным сопротивлением. Его источником являются катушки. Они представляют собой двухполюсник, намотанный медным эмалированным проводом (обычно это ПЭТВ) на ферритовый или железный сердечник. Подобные детали встречаются в широком перечне оборудования: от древних советских радиоприёмников до материнских плат ПК последних моделей.
Катушки индуктивности
Виды сопротивления и их особенности
Если в цепи постоянное напряжение, то, зная её сопротивление, можно узнать силу тока при помощи закона Ома. Он говорит о том, что сила тока пропорциональна напряжению, которое является его причиной. Коэффициент пропорциональности представляет обычное сопротивление. Его принято называть активным.
Если напряжение является постоянным, то сопротивление будет только активным. Его значение определяет, сколько энергии электрического поля преобразовано в тепло, то есть, безвозвратно утрачено. Поэтому при работе с кабелями СИП-3 1×50, СИП-2 3×70 и другими нужно помнить, что потери энергии из-за активного сопротивления могут быть значительными.
Более распространено использование переменного тока. Он возникает под воздействием напряжения, циклически изменяющегося по синусоидальному закону. Такой ток порождает реактивное сопротивление, которое дополняет действие активного. Существует две разновидности реактивного сопротивления различной природы — на основе индуктивности или емкости. Их отличительной особенностью является то, что они способствуют не трате электроэнергии, а преобразованию её в другую форму.
Нужно учитывать, что применение различных видов кабелей связано не только с наличием активного сопротивления, но и реактивного. Например, кабели СИП-3 1×50, СИП-2 3×70, АС-95 могут использоваться в электросетях и с активным, и индуктивным, и емкостным сопротивлениями.
Чтобы понять, что собой представляет индуктивное сопротивление, можно представить цепь, в которой имеется катушка, подключённая к источнику переменного тока. Как известно, напряжение меняется по синусоидальному закону. При этих изменениях катушка будет создавать магнитное поле, которое будет, в частности, влиять на текущий через него ток. Согласно природе магнитного поля, при уменьшении тока магнитное поле способствует его увеличению, а при усилении наблюдается противоположный эффект. Кроме того, цепь переменного тока с активным сопротивлением тратит энергию на выделение тепла.
На практике речь идёт о действии индуктивного сопротивления, обеспечивающего сдвиг фазы между током и напряжением. Движение зарядов создаёт поле, которое в свою очередь препятствует изменению тока. Такое сопротивление присутствует не только в катушках, но и, например, при использовании кабеля СИП-2 3×70.
Емкостное сопротивление имеет другую природу. Для объяснения следует рассмотреть цепь, состоящую из источника переменного тока и конденсатора. Последний представляет собой деталь, в которой две поверхности параллельны друг другу и не имеют непосредственного электрического контакта.
При использовании постоянного тока на обкладках конденсатора накапливаются заряды: на одной — положительный, а на второй — отрицательный. Электрополе за счет накопленного заряда представляет собой источник, противодействующий току. Поэтому конденсатор в цепи постоянного тока является бесконечно большим сопротивлением. Ток не проходит сквозь диэлектрик, разделяющий обкладки конденсатора.
В цепи переменного тока конденсатор циклически заряжается и разряжается, обеспечивая движение электрозарядов. Данный процесс в цепи переменного тока с активным и реактивным сопротивлением будет происходить с опозданием относительно синусоидального изменения напряжения. Таким образом, конденсатор представляет собой конечное сопротивление, получившее название емкостного.
Разница между емкостным и индуктивным сопротивлением заключается в том, что через индуктивную катушку постоянный ток протекает, а при использовании конденсатора пройти не может. Однако переменный ток в обеих цепях может течь без каких-либо проблем.
Какие отличия
Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.
Индуктивная величина и ее формулы
Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть. Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть
То есть, в окружающую среду полученная энергия не передается
Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.
Комплексная сопротивляемость отдельного элетроэлемента сети R
В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.
Активная сопротивляемость в цепи переменного синусоидального тока
Что зовется индуктивным сопротивлением
Когда на катушку подают переменное напряжение, ток, проходящий по ней, меняется согласно поданному напряжению. Это служит причиной изменения магнитного поля, создающего электродвижущую силу, препятствующую происходящему.
Схема для измерения
В такой цепи имеется зависимость электрических параметров от двух видов: обычного и индуктивного. Они обозначаются, соответственно, как R и XL.
На обычном происходит выделение мощности. Однако на реактивных элементах она является нулевой. Это связано с постоянным изменением направления переменного тока.
В течение одного периода колебаний энергия дважды закачивается в катушку и столько же раз возвращается в источник.
Определение индуктивности
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
R = P/I2
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = Imsinωt. Требуется определить напряжение в цепи и мощность. При переменном токе в катушке возникает э. д. с. самоиндукции eL поэтому ток зависит от действия приложенного напряжения и эдс eL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:
Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых uR равно падению напряжения в активном сопротивлении, а другое uL уравновешивает эдс самоиндукции.
В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б). Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — uR совпадает по фазе с током, UL опережает ток на 90°.
Поэтому:
u = R*Imsinωt + ωLImsin(ωt+π/2).
Принцип действия индуктивного сопротивления линий
Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.
Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.
Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
- Универсальная, может совмещать сразу несколько вариантов обмотки.
Независимо от конструкции, все катушки работают по одному и тому же принципу.
От каких факторов зависит сопротивление
Изменение силы тока создает электромагнитное поле переменной интенсивности. Результатом его воздействия на проводник является противодействие происходящему изменению тока.
Это противодействие называется реактивным сопротивлением. Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.
В ситуации, когда в цепи присутствует катушка, ее реакция усиливается по мере увеличения частоты.
Цепь, в которой возникает индукция
В случае, когда ее индуктивность уменьшается, то противодействующая сила также становится меньше. При увеличении она возрастает.
Индуктивное сопротивление существенно связано с тем, какую форму принимает проводник. Оно имеется также и у отдельного провода, лежащего прямо. Однако если рядом будет еще один, то он будет оказывать воздействие дополнительно, что повлияет на рассматриваемую величину.
Рассматриваемую характеристику отдельного провода можно определять в зависимости от его толщины, но оно никак не связано с его сечением.
Принцип действия электродвижущей силы
Емкостная проводимость линий
Электрические линии, кроме активного и индуктивного сопротивлений, характеризуются и емкостной проводимостью, которая обусловлена емкостью между проводами и между проводам и землей.
Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:
Из данной формулы видно, что рабочая емкость будет увеличиваться с увеличением сечения проводов и уменьшением расстояния между ними. Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.
Емкостная проводимость одноцепной воздушной линии определяется по формуле:
Определение рабочей емкости кабельной линии по формулам, в которые входят диэлектрическая проницаемость изоляции кабеля, геометрические размеры и другие конструктивные особенности, задача не из легких, поэтому значения рабочей емкости определяют по специальным таблицам, составленным заводом изготовителем для различных марок кабелей, в зависимости от их номинального напряжения.
Емкостной ток вначале линии при холостом ходе (при отключенных электроприемниках) можно определить из формулы:
Где: U – линейное напряжение сети, В; l – длина линии, км;
Емкостные токи имеют серьезное значение в воздушных линиях с рабочим напряжением 110 кВ и выше и в кабельных линиях с напряжением выше 10 кВ. При расчете электрических сетей с напряжениями ниже, чем выше перечисленные, емкость линии могут не учитывать. Емкость токопроводящих частей линии по отношению к земле имеет значение при расчете заземляющих устройств и защиты.
В сети с изолированной нейтралью величину емкостного тока однофазного замыкания на землю приближенно можно определить по формулам:
Для воздушной линии:
Для кабельной линии:
Катушка индуктивности
Он представляет собой изолированный провод, многократно намотанный вокруг сердечника.
Обычно каркас имеет цилиндрическую или тороидальную форму.
Индуктивность рассматривается в качестве основной характеристики катушки. Это качество выражает способность элемента осуществлять преобразование переменного тока в магнитное поле.
Важно! Магнитные свойства существуют даже у одиночного провода, при условии, что изменяется проходящий через него ток. Воздействие поля направлено так, чтобы противодействовать его изменению. Если он будет увеличиться, поле будет его тормозить, а если ослабевать — усиливать.
Катушки индуктивности
Определение направления силовых линий подчиняется «правилу большого пальца»: если у сжатой в кулак руки большой палец указывает в направлении изменения силы тока, то сомкнутые пальцы подсказывают направление силовых линий поля.
Таким образом в том случае, если провод многократно намотан на цилиндрическое основание, то силовые линии от разных витков складываются и проходят через ось.
Будет интересно➡ Контрольно-измерительные приборы. Виды и область применения
Для того, чтобы многократно увеличить индуктивность, в центр цилиндра помещают сердечник из ферромагнитного материала.
Соленоид
Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:
df : dt = L dl : dt.
Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.
- Первая способна контролировать линейное давление.
- Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
- Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
- Четвертая управляется гидравлическим способом или клапанами.
Формулы, зависимости и виды индуктивности
Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:
Y = LI.
Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.
Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуляПростой DC-DC повышающий преобразователь
Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.
Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.
Соотношение между фазами U и I на X L
Так как активное сопротивление катушки по условию равно нулю (чисто индуктивное сопротивление), то все напряжение приложенное генератором к катушке идет на преодоление э. д. с. самоиндукции катушки. Это значит что график напряжения приложенного генератором к катушке равен по амплитуде графику э. д. с. самоиндукции катушки и находится с ним в противофазе.
Напряжение приложенное генератором к чисто индуктивному сопротивлению и ток идущий от генератора по чисто индуктивному сопротивлению сдвинуты по фазе на 90 0 ,т. е. напряжение опережает ток на 90 0.
Реальная катушка кроме индуктивного сопротивления имеет еще и активное сопротивление. Эти сопротивления следует считать соединенными последовательно.
На активном сопротивлении катушки напряжение приложенное генератором и ток идущий от генератора совпадают по фазе.
На чисто индуктивном сопротивлении напряжение приложенное генератором и ток идущий от генератора сдвинуты по фазе на 90 0 . Напряжение опережает ток на 90 0 . Результирующее напряжение приложенное генератором к катушке определяется по правилу параллелограмма.
кликните по картинке чтобы увеличить
Результирующее напряжение приложенное генератором к катушке всегда опережает ток на на угол меньший 90 0 .
Величина угла φ зависит от величин активного и индуктивного сопротивлений катушки.
О результирующем сопротивлении катушки
Результирующее сопротивление катушки нельзя находить суммированием величин её активного и реактивного сопротивлений
.
Результирующее сопротивление катушки Z равно
Катушка индуктивности в цепи переменного тока
Катушка индуктивности в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то катушки индуктивности противостоят изменению проходящего через них тока (напряжение на них прямопропоционально скорости изменения тока). Согласно Закону Ленца, индуцированное напряжение всегда имеет такую полярность, которая пытается сохранить текущее значение силы тока. То есть, если величина тока возрастает, то индуцированное напряжение будет «тормозить» поток электронов; если величина тока уменьшается, то полярность напряжения развернется и будет «помогать» электронному потоку оставаться на прежнем уровне. Такое противостояние изменению величины тока называется реактивным сопротивлением.
Математическая взаимосвязь между напряжением на катушке индуктивности и скоростью изменения тока через нее выглядит следующим образом:
Отношение di/dt представляет собой скорость изменения мгновенного тока (i) с течением времени, и измеряется в амперах в секунду. Индуктивность (L) измеряется в Генри, а мгновенное напряжение (u) – в вольтах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую индуктивную схему:
Простая индуктивная цепь: ток катушки отстает от напряжения на 90 o .
Если мы построим график тока и напряжения для этой простой цепи , то он будет выглядеть примерно так:
Как вы помните, изменение напряжения на катушке индуктивности является реакцией на изменение тока, проходящего через нее. Отсюда можно сделать вывод, что мгновенное напряжение равно нулю всякий раз, когда мгновенное значение тока находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны тока), и мгновенное напряжение равно своему пиковому значению всякий раз, когда мгновенный ток находится в точках максимального изменения (точки самого крутого наклона волны тока, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на 90 o не совпадает по фазе с волной тока. На графике видно, как волна напряжения дает «фору» волне тока: напряжение «ведет» ток, а ток «запаздывает» за напряжением.
Читать также: Как сделать свето музыку на колонку
Ели мы на этот график нанесем значения мощности нашей схемы, то все станет еще более интересным:
Поскольку мгновенная мощность представляет собой произведение мгновенного напряжения и мгновенного тока (p = iu), она будет равна нулю, если мгновенное напряжение или ток будут равны нулю. Всякий раз, когда мгновенные значения тока и напряжения имеют положительные значения (выше нулевой линии), мощность так же будет положительна. Аналогично примеру с резистивной цепью, мощность примет положительное значение и в том случае, если мгновенный ток и напряжение будут иметь отрицательные значения (ниже нулевой линии). Однако, вследствие того, что волны напряжения и тока не совпадают по фазе на 90 o , бывают случаи, когда ток положителен, а напряжение отрицательно (или наоборот), в результате чего появляются отрицательные значения мгновенной мощности.
Но, что такое отрицательная мощность? Отрицательная мощность означает, что катушка индуктивности отдает энергию обратно в цепь. Положительная же мощность означает, что катушка индуктивности поглощает энергию из цепи. Так как положительные и отрицательные циклы питания равны по величине и продолжительности, в течение полного цикла катушка индуктивности отдает обратно в схему столько же энергии, сколько она потребляет из нее. В практическом смысле это означает, что реактивное сопротивление катушки не рассеивает никакой энергии, чем оно и отличается от сопротивления резистора, рассеивающего энергию в виде тепла. Однако, все вышесказанное справедливо только для идеальных катушек индуктивности, провода которых не имеют никакого сопротивления.
Сопротивление катушки индуктивности, изменяющее силу тока, интерпретируется как сопротивление переменному току в целом, у которого по определению постоянно меняется мгновенная величина и направление. Это сопротивление переменному току похоже на обычное сопротивление, но отличается от него тем, что всегда приводит к фазовому сдвигу между током и напряжением, а так же рассеивает нулевую мощность. Из-за указанных различий, данное сопротивление носит несколько иное название – реактивное сопротивление. Реактивное сопротивление, как и обычное, измеряется в Омах, только обозначается оно символом Х, а не R. Для большей конкретики, реактивное сопротивление катушки индуктивности обычно обозначают заглавной буквой Х с буквой L в качестве индекса: X L .
Поскольку напряжение на катушке индуктивности пропорционально скорости изменения тока, оно будет больше для быстро меняющихся токов, и меньше – для токов с более медленным изменением. Это означает, что реактивное сопротивление любой катушки индуктивности (в Омах) прямопропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления выглядит следующим образом:
Если на катушку индуктивностью 10 мГн воздействовать частотами 60, 120 и 2500 Гц, то ее реактивное сопротивление примет следующие значения:
В уравнении реактивного сопротивления выражение “2πf” имеет важное значение. Оно означает число в радианах в секунду, характеризующее «вращение» переменного тока (один полный цикл переменного тока представляет собой одно полное круговое вращение). Радиан – это единица измерения углов: в одном полном круге есть 2π радиан, точно так же, как в нем есть 360 o . Если генератор переменного тока двухполюсный, то он произведет один полный цикл для каждого полного оборота вала, что будет означать 2π радиан или 360 o . Если постоянную 2π умножить на частоту в герцах (циклах в секунду), то результатом будет число в радианах в секунду, известное как угловая (циклическая) частота переменного тока.
Помимо выражения 2πf, угловая частота переменного тока может обозначаться строчной греческой буквой ω (Омега). В этом случае формула X L = 2πfL может быть написана как X L = ωL.
Необходимо понимать, что угловая частота является выражением того, насколько быстро проходит полный цикл волны, равный 2π радиан. Она необязательно представляет фактическую скорость вала генератора, производящего переменный ток. Если генератор имеет более двух полюсов, его угловая частота будет кратной скорости вращения вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, чтобы отличить ее от механического движения.
При любом способе выражения угловой частоты очевидно, что она прямопропорциональна реактивному сопротивлению катушки индуктивности. При увеличении частоты переменного тока (или скорости вращения вала генератора), катушка индуктивности будет оказывать большее сопротивление прохождению тока и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление катушки индуктивности (в Омах). Как видите, это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:
Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, напряжение имеет фазовый сдвиг +90 o по отношению к току (рисунок ниже). Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что сопротивление катушки индуктивности переменному току обладает следующим фазовым углом:
Ток на катушке индуктивности отстает от напряжения на 90 o .
Математически можно сказать, что фазовый угол сопротивления катушки индуктивности переменному току составляет 90 o . Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом. Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).
Расчёт индуктивного сопротивления катушки
Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.
Полное сопротивление
Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:
L=u0urN2S/l,
где:
- u0 – магнитная проницаемость вакуума — 4p*10-7 Гн/м;
- ur – относительная проницаемость сердечника;
- N – количество витков дросселя;
- S – его поперечное сечение в м2;
- l – длина катушки в метрах.
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.
Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.
Какие параметры есть у катушки
От того, где будет применяться индуктивный элемент и на какой частоте работать, зависит его исполнение. Имеются общие параметры:
- L – индуктивность;
- R пот – сопротивление потерь;
- Q – добротность;
- свой резонанс и паразитарная ёмкость;
- коэффициенты ТКИ и ТКД.
Индуктивность (коэффициент самоиндукции) L – это главная электрическая характеристика элемента, которая показывает количество накапливаемой дросселем энергии при передвижении тока. Величина энергии в катушки тем выше, чем больше её индуктивность. Единица измерений L – 1 Гн.
При взаимодействии тока и магнитного поля в обмотке возникают вредные явления. Они способствуют возникновению потерь, которые обозначают R пот. Формула потерь имеет вид:
R пот = rω + rd + rs + re.
Слагаемые формулы – это потери:
- rω – в проводах;
- rd – в диэлектрике;
- rs – в сердечнике;
- re – на вихревые токи.
В результате таких потерь импеданс индуктивного двухполюсника нельзя назвать целиком реактивным.
Добротность двухполюсника определяется по формуле:
Q = ω*L/R пот,
где ω*L = 2π*L – реактивное сопротивление.
При наматывании витков элемента между ними возникает ненужная ёмкость. Из-за этого дроссель превращается в колебательный контур с собственным резонансом.
ТКИ – показатель, описывающий зависимость L от Т0С.
ТКД – показатель, описывающий зависимость добротности от Т0С.
Информация. Изменение основных параметров индуктивного двухполюсника зависит от коэффициентов ТКИ, ТКД, а также от времени и влажности.
Индуктивность в цепи постоянного тока
Для лучшего понимания происходящих процессов в катушке, рассмотрим, что происходит в катушке при подаче на нее постоянного напряжения.
При подключении источника питания к катушке в ней начинает протекать ток, который создает вокруг неё магнитное поле. Магнитные силовые линии поля распространяются через витки катушки наружу пересекая их, и образуют при этом ЭДС самоиндукции. Эта ЭДС, согласно правилу Ленца, будет препятствовать мгновенному нарастанию тока в катушке. Нарастание тока происходит постепенно, по экспоненциальному закону. Через небольшой промежуток времени переходной процесс заканчивается, и ток достигает своего нормального значения. Продолжительность нарастания тока в секундах определяется по формуле:
t=3L/R,
где L – индуктивность катушки в генри, а R – общее сопротивление всей цепи в омах. Если, к примеру, индуктивность катушки L=0,6 Г, а сопротивление цепи R=60 Ом, тогда длительность переходного процесса будет равна: t=3•0,6/60=0,03 сек.
Будет интересно➡ Витая пара: категории, обжим, советы по работе
При отключении батареи от катушки индуктивность тоже происходит переходный процесс (такой опыт с первичной обмоткой трансформатора показан на странице “Электромагнетизм” рис.е). В этом случае силовые магнитные линии будут приближаться к центру катушки опять пересекая ее витки. Создается ЭДС самоиндукции, которая уже направлена не против тока, а (опять же по правилу Ленца) совпадающая с направлением прерванного тока.
Если катушка имеет большую индуктивность (в нашем опыте катушкой является первичная обмотки трансформатора с большим количеством витков и значительным железным сердечником) и через нее протекал большой ток, то тогда ЭДС самоиндукции, появляющая на концах катушки индуктивности, может достигать величины во много раз больше напряжения источника питания. Это объясняется тем, что при размыкании питающей сети энергия, запасенная в магнитном поле катушки, не исчезает, а превращается в ток. Напряжение между концами катушки индуктивности может достигать таких значений, которое способно привести к пробою между обмотками, а так же выводу из строя полупроводниковых приборов. Это надо надо учитывать на практике при работе с приборами, имеющие катушки с большой индуктивностью через которые проходит значительный ток.
Как измерить в домашних условиях
Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.
Порядок действий следующий:
- При помощи омметра определяют активное сопротивление обмотки R.
- Подключают трансформатор последовательно с амперметром в сеть.
- Параллельно обмотке подключают вольтметр.
- По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
- Индуктивное сопротивление находят, вычитая из полного сопротивления активное: XL=Z-R
- Индуктивность определяется по формуле: L=XL/(2πf), где π – число пи 3.14, f – частота измерений.
Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.
Индуктивность в цепи переменного тока
Для опытов с постоянным током катушка индуктивности намотана тонким проводом с большим количеством витков. Это делается для того, чтобы при подаче на нее напряжения с мощного источника питания витки катушки не перегорели, т.к. при намотке витков толстым проводом сопротивление будет маленьким, а ток через нее большой (по закону Ома для постоянного тока I=U/R) и она может сгореть. Сопротивление катушки индуктивности постоянному току (которое можно измерить мультиметром) называется активным сопротивлением.
Будет иначе, если в цепь катушки подать переменный ток. При этом магнитное поле катушки индуктивности становится тоже переменным. На рисунке показано, как меняется магнитное поле при синусоидальном токе. Во время периода магнитное поле меняет как свою силу, так и свое направление по синусоидальному закону. А это значит, что при этом возникает ЭДС самоиндукции, которая, согласно правилу Ленца, будет препятствовать приложенному извне напряжению.
Рассмотрим график происходящих процессов в катушке индуктивности. При включения катушки в цепь переменного тока в первую четверть периода ( 0º-90º) на катушку поступает нарастающее напряжение и ее магнитное поле “расширяется”, накапливая магнитную энергию. Ток, в этот момент, противодействующей ЭДС самоиндукции, максимальный и противоположный по знаку с напряжением на катушке. За другую четверть периода (90º-180º), когда напряжение на катушке индуктивности уменьшается, магнитное поле “сворачивается”, индуцируя ЭДС самоиндукции, которое совпадает с направлением тока. Этот ток самоиндукции в катушке старается уже “помочь” уменьшающему переменному току сохранить достигнутый большой магнитный поток. В этот полупериод катушка индуктивности уже не потребляет, а отдает энергию обратно генератору. Следовательно, происходит постоянный обмен энергий между генератором и катушкой. А это означает, что средняя мощность потребления катушки равна нулю. Благодаря разнице фаз тока и напряжения в 90º, катушка индуктивности имеет реактивную мощность и, соответственно, реактивное сопротивление, как и конденсатор. Разница лишь в том, что в катушке индуктивности напряжение опережает ток, а в конденсаторе – наоборот. Реактивное (индуктивное) сопротивление катушки, в отличии от ее активного сопротивления, не вызывает безвозвратных потерь энергии.
Допустим, возьмем идеальную катушку, в которой не учитываются сопротивления провода и другие потери. Тогда катушка индуктивности окажет переменному напряжению индуктивное сопротивление XL,которое измеряется в омах и вычисляется по формуле:
где f – частота тока в герцах (Гц), а L – индуктивность катушки в генри (Г). Отсюда видно, что величина индуктивного сопротивления катушки зависит от частоты и индуктивности. Чем выше частота тока и больше индуктивность катушки, тем больше индуктивное сопротивление.
К примеру, найдем индуктивное сопротивление катушки индуктивностью 5Г на частоте 50Гц. XL=2π•50•5=1570 Ом. На частоте 1кГц эта катушка будет иметь индуктивное сопротивление 31кОм, а на 1МГц – 31МОм. На графике показана зависимость упомянутой катушки от частоты.
Теперь, зная значение индуктивного сопротивления, можно записать закон Ома при переменном токе через катушку:
Например,найдем ток, который протекает через идеальную катушку с индуктивностью L=500 мкГ, если ее подключить к переменному напряжению U=0,4 В и частотой f=500 кГц. I= 0,4/2•3,14•5•103•500•10-6=0,25 мА
В реальной катушке нужно учитывать не только индуктивное сопротивление, но и сопротивление потерь Rпот. На низких частотах Rпот равно только сопротивлению провода катушки. При повышении частоты на катушке сопротивление потерь будет возрастать за счет появления других потерь (вихревые токи, поверхностный эффект проводника и т.д.) (рис.а). Поэтому полное сопротивление катушки индуктивности переменному току на средних частотах равно: и называется импедансом. На высоких частотах начинает оказывать еще влияние cобственная (паразитная) емкость катушки Спараз, которая шунтирует индуктивность (рис.b).
Основными параметрами высокочастотных катушек индуктивности являются индуктивность, добротность и собственная емкость. Индуктивность зависит от количества витков, размера катушки и наличия ферромагнитного сердечника. Чем больше намотано витков на катушке, тем больше ее индуктивность. А наличие сердечника увеличит индуктивность катушки. Добротность определяет качество катушки индуктивности и равна отношению индукнивного сопротивления к сопротивлению потерь: Чем больше добротность, тем качественнее катушка. Катушкой хорошего качества считается катушка с добротностью от 50 до 200. Чтобы достигнуть такого качества используют следующие средства: – применением сердечников, при которых увеличивается индуктивность при меньшем числе витков катушки (т.е. уменьшается сопротивление провода); – увеличение толщины провода, что, правда, увеличит габариты катушки; – в диапазоне длинных и средних волн применение провода литцендрат, который состоит из определенного количества проволочек изолированных друг от друга. Собственная емкость катушки индуктивности обусловлена емкостью обмотки и является нежелательной. Для ее уменьшения применяются различные способы намотки катушки. Одним из способов является перекрестная намотка типа “универсаль” (рис.c). Так же применяется намотка витков не плотно друг к другу, а на определенном расстоянии с принудительным шагом)(рис.d,e).
Расчет эквивалентного сопротивления элементов цепи
Определение общего цепного сопротивления будет зависеть от того, какого типа конфигурацию составляют компоненты цепи. Для параллельного и последовательного подключений правила расчета будут неодинаковыми. Опираться при вычислениях нужно на закон Ома.
Согласно ему, у всех последовательно соединенных деталей, подключенных в цепь переменного тока, будет одно и то же значение электротока:
I=U/Z, где Z – общий импеданс цепи.
Напряжения будут различаться и окажутся привязанными к сопротивлениям деталей: на концах резистора его значение будет равно UR = IR (здесь R – активная резистивность элемента), для дросселя – UL = IXL, для емкостного элемента – UC = IXC (XL и XC – реактивные показатели соответствующих устройств). Так как векторы напряженности катушки и конденсатора имеют противоположные направления, суммарный показатель на реактивных деталях будет равен: UX = UL – UC . Противодействие будет равно: X = XL – XC.
Напряжения (общее, реактивное и активное) могут быть представлены в виде прямоугольного треугольника. Из него получается, что U² = UR² + UX². Поскольку противодействия входящих в цепь компонентов пропорциональны напряжениям, имеем Z2=R2+X2=R2+(XL – XC)2.
Для параллельного соединения принято выводить значения импеданса из проводимостей элементов, которые обратны их сопротивлениям. Отсюда 1/z2 = 1/R2 + 1/X2. Таким образом, выходит следующая формула:
Z2=1/(1/R2+(1/ XL – 1/ XC)2).
Общее сопротивление определяется компонентным составом цепи и характером соединения ее элементов. При расчетах показателей используется закон Ома.
Сопротивление изоляции кабеля
Для нахождения R изоляции кабеля нужно исходить из его вида. Есть следующие разновидности:
- 1000 В и больше — высоковольтные.
- Ниже 1000 В — низковольтные.
- Контрольные электрокабели — защитные цепи, вторичные цепи РУ (реле указательных), цепи питания электроприводов и так далее.
Для измерения R изоляции необходимо специализированное устройство. Высоковольтные и низковольтные определяются при напряжении 2500 В, когда контрольные — от 500 до 2500 В. Если используется высоковольтный со значением больше 1000 В, то его R изоляции должно быть не меньше 10 МОм. Если используется низковольтный со значением меньше 1000 В, то его R изоляции должно быть не меньше 0,5 Мом. У контрольных кабелей R изоляции должно быть не меньше 1 МОм.