Что такое электрическая ёмкость, в чём измеряется и от чего зависит

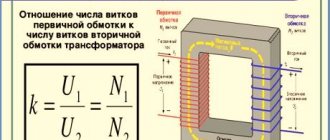
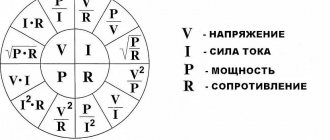
От чего зависит емкость и заряд конденсатора

Емкость конденсатора это физическая величина по которой производится оценка его возможностей выполнять свои функциональные задачи.

Практическое значение емкости выражается в способности электрического устройства к накоплению заряда.

Величина напряжения на пластинах в прямой пропорции влияет на количественные характеристики заряда на обкладках. Формула определения емкости выглядит как

C = q/U,

где С — емкость конденсатора,

q — означает количество заряда на одной из пластин,

U — разница потенциалов на обкладках. Приведенная формула расчета имеет в большей степени теоретический характер.

Существует иное определение емкости, которое полезнее в практическом смысле.

В формуле C = єS/d обозначена ее связь с площадью S обкладок, расстоянием между пластинами d и свойствами диэлектрика є.

Из формулы следует, что чем больше площадь обкладок, тем больший заряд может на них разместиться и чем больше расстояние между пластинами, тем слабее заряженные частицы будут притягиваться друг к другу, увеличивая их шансы покинуть обкладку.

Максимальная диэлектрическая проницаемость материала, расположенного между пластинами, увеличивает емкость конденсатора без изменения габаритных характеристик.

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Как устроен конденсатор

Конденсатор состоит из двух или нескольких металлических пластин, между которыми располагается диэлектрический материал. Электроны начинают двигаться, но не в состоянии преодолеть диэлектрик, из-за этого между пластинами накапливается электрический заряд.

Хорошими диэлектрическими свойствами обладают бумага покрытая оксидом алюминия, слюда, электролит, керамика и подобные материалы.

Заряды на разных обкладках одинаковые по величине, но противоположные по знаку.

Гальванометром

При наличии баллистического гальванометра также можно определить ёмкость конденсатора. Для этого используют формулу:

C = α * Cq / U , где α – угол отклонения гальванометра, Cq – баллистическая постоянная прибора, U – показания гальванометра.

Из-за падения сопротивления утечки ёмкость конденсаторов уменьшается. Энергия теряется вместе с током утечки.

Описанные выше методики определения ёмкости позволяют определить исправность конденсаторов. Значительное отклонение от номиналов говорит, что конденсаторы неисправны. Пробитый электролитический радиоэлемент легко определяется путём измерения сопротивления. Если сопротивление стремится к 0 – изделие закорочено, а если к бесконечности – значит, есть обрыв.

Следует опасаться сильного электрического разряда при подключениях щупов к большим электролитам. Они могут накапливать мощный электрический заряд от постоянного тока, который молниеносно высвобождается током разряда.

Виды конденсаторов

Конденсаторы различаются по целому ряду параметров: по конфигурации, по типу диэлектрика, по материалу обкладок, по виду изменения емкости (постоянные, переменные, подстрочные), по рабочему напряжению. Ниже на рисунке рассмотрим основные виды электрических устройств различной конфигурации.

Плоский

Плоский вид устройства, – это две пластины, которые располагаются параллельно друг против друга. Они отличаются компактностью, сохраняя при этом большую емкость.

Емкость плоского конденсатора возрастает по мере увеличения площади пластин и при уменьшении расстояния между ними.

Для расчета емкости плоского конденсатора следует пользоваться формулой C = ε0 εS / d

Сферический

Сферический конденсатор представляет собой две концентрично расположенные сферы с находящимся между ними тонким диэлектриком. Наружную поверхность внешней обкладки заземляют для создания электрического поля непосредственно между обкладками. С учетом геометрии обкладок расчет емкости сферического конденсатора производится по формуле

C = 4πεε0 Rr/ R — r, где R — радиус наружной обкладки, r — радиус внутренней.

Цилиндрический

Цилиндрический конденсатор выполнен из двух полых цилиндров с разными радиусами образующих их окружностей с общей осью. Между наружной поверхностью малого цилиндра и внутренней поверхностью большого находится диэлектрик. Для расчета емкости цилиндрического конденсатора можно воспользоваться формулой C = 2πєє0L/ ln (R2/R1),

где L — длина цилиндрических обкладок,

R2 — радиус наружного цилиндра,

R1 — радиус внутреннего цилиндра,

ln — обозначение логарифмического действия.

Что такое конденсатор

Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.

Конденсатор

Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).

Термин из учебного пособия

Полярные

Полярные конденсаторы – это приборы, имеющие полярность, а именно плюс и минус. Важно чтобы плюсовой контакт был соединен с «плюсом» источника питания, а минусовой с его «минусом». Нарушение полярности может привести даже к взрыву конденсатора. К полярным принадлежат танталовые, ионисторы, конденсаторы с электролитическим диэлектриком.

Танталовые

В танталовых конденсаторах, относящихся к электролитическому типу, в качестве диэлектрика используется спеченный танталовый порошок оксид тантала, отсюда происходит их название. Такой диэлектрик сводит практически к нулю ток утечки.

Недостаток заключается в невозможности работать в электрических цепях с высоким напряжением.

Танталовый конденсатор включает в себя 4 элемента – анод, диэлектрик, электролит и катод.

В отличие от электролитических танталовые имеют меньшую собственную индуктивность, благодаря чему их можно применять на высоких частотах.

Компактность танталовых устройств позволяет их использовать в качестве составляющих монтажных схем.

Ионисторы

Ионисторы принадлежат к разряду электрохимических конденсаторов. Особенность конструкции заключается в сочетании свойств обычного конденсатора и аккумуляторной батареи. Пространство между электродами заполняется твердым электролитом на основе рубидия и аналогичных материалов. Такая конструкция исключает самопроизвольный разряд ионистора.

Быстрая разрядка и зарядка делают возможным его использование в некоторых видах электрических схем вместо аккумулятора.

Аккумулятор, в отличие от ионистора, потребует значительное время для своей зарядки. Емкость ионистора отличается повышенным значением среди всех электролитических устройств.

Работает ионистор только с источником постоянного напряжения.

Электролитические

Большое распространение получили электролитические конденсаторы, у которых одна из обкладок выполнена в виде алюминиевой фольги. Другой обкладкой служит твердый или жидкий электролит обеспечивающий движение заряженных частиц для сохранения оксидной пленки.

Емкость электролитического конденсатора на сегодняшний день является наибольшей при соотношении емкости и объема элемента.

Электролитические элементы устанавливаются в фильтрах, но важно соблюдение полярности.

По сравнению с танталовыми конденсаторами в электролитических идут значительный ток утечки.

Процессы переноса заряженных частиц происходят медленно, что увеличивает количество выделяемого тепла. Отсюда перегрев и низкий срок службы.

Как правильно соединять конденсаторы?

У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”

Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!

Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?

Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.

В реальности это выглядит так:

Параллельное соединение Принципиальная схема параллельного соединения Последовательное соединение Принципиальная схема последовательного соединения

Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.

Неполярные

Неполярные конденсаторы корректно работают при любых вариантах подключения их в электрическую схему.

Это связано с похожей структурой материалов образующих границу между обкладкой и диэлектриком. Стороны одинаковы. Все это приводит к тому, что во время установки конденсатора нет необходимости соблюдать полярность. В качестве неполярных электрических устройств в основном используются сухие, реже электролитические, изготовленные по измененной технологии.

Керамические

Керамические конденсаторы имеют высокие электрические показатели, маленькие габариты и приемлемую стоимость.

Устанавливаются элементы в контурах радиоаппаратуры. Керамические конденсаторы подразделяются на

• с постоянной емкостью
• подстроечные.

Элементы с постоянной емкостью – устанавливают в контурах генераторов и гетеродинов. Подстроечные – используются для подгонки параметров колебательных контуров. Широкое распространение получили благодаря разнообразию емкостей, широкому диапазону рабочих напряжений, стандартными типоразмерами аналогичными керамическим устройствам разных производителей.

Пленочные

Особенностью таких устройств будет диэлектрик в виде пленки. Пленка изготавливается из фторопласта, металлизированной бумаги, полипропилена, поликарбоната и подобных материалов. Металлическая пленка или фольга напыляются или напрессовываются на диэлектрик.

Благодаря большому количества слоев – получается увеличение площади, соответственно, существенно увеличивается емкость.

Из достоинств пленочного конденсатора следует отметить сравнительно высокую надежность, стабильность теплового состояния при действии нагрузок вызванных переменным током.

К недостаткам можно отнести невысокое значение диэлектрической проходимости.

Пленочные конденсаторы используются в цепях постоянного тока, всевозможных фильтрах и резонансных схемах.

Smd

В цепях управления некоторых видов плат используются небольшие по размерам Smd конденсаторы, имеющие форму маленьких кирпичиков. На плату радиоэлемент устанавливается посредством правила поверхностного монтажа. Smd устройства бывают следующих видов:

• электролитические
• керамические;
• танталовые.

Керамические SMD конденсаторы, имеющие диэлектрик с высокой проницаемостью, маркируются тремя буквами. Первыми двумя буквами обозначается нижняя и верхняя предельно допустимая граница рабочего диапазона температур, третья буква используется при обозначении отклонений изменения емкости для измеряемых диапазонов.

Маленькие размеры Smd конденсаторов не всегда позволяют нанести маркировку на корпус или она будет очень мелкая.

В таких случаях без специального измерительного прибора, например, мультиметра не обойтись.

Где и для чего используются

Как уже говорили, сложно найти схему без конденсаторов. Их применяют для решения самых разных задач:

• Для сглаживания скачков сетевого напряжения. В таком случае их ставят на входе устройств, перед микросхемами, которые требовательны к параметрам питания.
• Для стабилизации выходного напряжения блоков питания. В таком случае надо искать их перед выходом. Часто можно увидеть электролитические цилиндрические конденсаторы
• Датчик прикосновения (тач-пады). В таких устройствах оной из «пластин» конденсаторов является человек. Вернее, его палец. Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения.
• Для задания необходимого ритма работы. Время заряда конденсаторов разной ёмкости отличается. При этом цикл заряд/разряд конденсатора остаётся величиной постоянной. Это и используется в цепях, где надо задавать определённый ритм работы.
• Ячейки памяти. Память компьютеров, телефонов и других устройств — это огромное количество маленьких конденсаторов. Если он заряжен — это единица, разряжен — ноль.
• Есть стартовые конденсаторы, которые помогают «разогнать» двигатель. Они накапливают заряд, потом резко его отдают, создавая требуемый «толчок» для разгона мотора.
• В фотовспышках. Принцип тот же. Сначала накапливается заряд, затем выдаётся, но преобразуется в свет.

Конденсаторы встречаются часто и область их применения широка. Но надо знать как правильно их подключить.

Переменные

Конденсаторы переменной емкости (КПЕ) состоят из части секций металлических пластин. Одна из них двигается плавно по отношению ко второй. Во время передвижения получается, что подвижные пластины (ротора), попадают в зазоры неподвижной пластины (статора). Благодаря процессу площадь перекрытия одних пластин другими изменяется, в результате чего изменяется у конденсатора емкость. Слоем диэлектрика в этом случае является воздух.

В конденсаторах, установленных в небольших устройствах, используется твердый диэлектрик, например, фторопласт или полиэтилен.

В старых радиоприемниках устройство применялось для настройки на определенную частоту колебательного контура работающей радиостанции.

Электрическое поле в диэлектрике

Если конденсатор НЕ подключен к источнику питания, заряд Q = CV на его крышках будет оставаться постоянным независимо от того, помещен ли диэлектрик между ними. Если мы обозначим C и E соответственно, емкость пустого конденсатора и значение электрического поля между его крышками, а C и E аналогичные значения для конденсатора, заполненного диэлектриком, мы можем записать

Отсюда и на основании определения диэлектрической проницаемости ε получаем

Таким образом, видно, что напряженность поля в диэлектрике в ε раз меньше, чем в вакууме.

Это соотношение является общим и применяется в каждом фиксированном поле E, независимо от его источника.

Максимальное рабочее напряжение на конденсаторе

Напряжение, подаваемое на конденсатор, не должно превышать максимальное, так как может произойти пробой диэлектрика и выход элемента из строя.

Для анализа работы конденсатора в цепи переменного тока критерием для сравнения со значением максимально возможного следует брать амплитудную величину напряжения.

Это значит, что если на нем обозначено какое то максимальное напряжение DC WV , то в действительности при включении в сеть оно должно быть на 1,4 меньше.

В чем измеряется напряжение конденсаторов

Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.

Измерение силы заряда двухполюсника

Величина и значение потери у конденсатора

Ток утечки конденсатора – критический фактор для использования, особенно если его применяют для силовой электроники. Потеря напрямую завязана со свойствами диэлектрика.

Никакой диэлектрик не способен со 100% гарантией изолировать металлические обкладки.

Через изолятор всегда будет проходить ток, меньший или больший в зависимости от свойств диэлектрика и теряться энергия. Кроме изолирующих способностей диэлектрика на ток утечки оказывают влияние следующие факторы:

• температура окружающего пространства;
• срок годности конденсатора без напряжения, температура;
• величина тока утечки прямо пропорциональна приложенному к обкладкам напряжению.

Восстановить работоспособность конденсатора после длительного хранения можно, приложив к нему рабочее напряжение с выдержкой в течение нескольких минут.

При этом этапе окислительный слой заново накапливается и восстанавливает работоспособность конденсатора.

Ток утечки конденсатора

Дело все в том, что какой бы ни был диэлектрик, конденсатор все равно рано или поздно разрядится, так как через диэлектрик, как ни странно, все равно течет ток. Величина этого тока у разных конденсаторов тоже разная. Электролитические конденсаторы обладают самым большим током утечки.

Также ток утечки зависит от напряжения между обкладками конденсатора. Здесь уже работает закон Ома: I=U/Rдиэлектрика . Поэтому, никогда не стоит подавать напряжение больше, чем максимально рабочее напряжение, прописанное в даташите или на самом конденсаторе.

Конденсатор в цепи электрического тока

Принцип работы конденсатора простой – подается напряжение и накапливается заряд. Накопитель по-разному ведет себя в двух вариантах электрической цепи.

Постоянного

Если в цепь с присоединенным к ней конденсатором подать ток, то стрелка на амперметре придет в движение, после чего быстро вернется в предыдущее положение. Это связано с тем, что прибор быстро заряжается и ток исчез. Через обкладки разделенные диэлектриком постоянный ток проходить не может. Практическое применение конденсатора в такой цепи вызывает много вопросов. В условиях постоянного тока конденсатор функционирует, но непродолжительное время. Переходные процессы в виде зарядки и разрядки снимают все сомнения. В электронных схемах на постоянном токе конденсаторы один из самых распространенных компонентов.

Переменного

При подключении переменного напряжения полюса конденсатора меняют плюс на минус с частотой подачи напряжения. В данном случае электроны передвигаются сначала в одну, а потом в другую. На обкладках при такой смене остаются излишки заряда, которые собственно и создают ток во внешней цепи.

Конденсатор в цепи переменного тога выступает в качестве резистора.

Конденсатор

Прежде чем разобраться с тем, что такое емкость простейшего конденсатора, необходимо определиться, что из себя представляет этот электроэлемент. Конденсатором является радиоэлектронная деталь, которая может накапливать и отдавать определенную порцию электрического заряда. Состоит устройство из следующих элементов:

1. Корпуса. Зачастую выполняется из алюминия. По форме он может быть плоским, сферическим и цилиндрическим.
2. Обкладок (2 и более). Их делают из металлических пластинок или фольги.
3. Диэлектрической прокладки. Устанавливается между обкладками и служит в качестве изолятора.
4. Двух или более выводных контактов для подключения устройства в электроцепь.

Работает такой накопитель электрического заряда следующим образом.

1. В момент подключения элемента к источнику электрического тока, он выступает в роли проводника. В этот момент электроток имеет максимальное значение, а напряжение — минимальное.
2. На обкладках элемента начинают скапливаться положительные и отрицательные заряды (электроны и ионы). Таким образом происходит зарядка самого устройства. На момент заряда сила электротока постепенно уменьшается, а напряжение наоборот — увеличивается.
3. После того как количество заряда в конденсаторе станет больше допустимого предела, он разряжается и процесс опять начинает повторяться циклически.

Основой работоспособности данного устройства является его емкость. Именно от этого параметра зависит время накопления заряда и общая «вместимость» устройства. О том, как на схемах обозначается простейший конденсатор, поможет понять следующий рисунок ниже.

Электрическая емкость, как и сами конденсаторы, нашли широкую область применения. Их используют в качестве:

1. Частотных фильтров.
2. Источника импульсов для различной фотоаппаратуры.
3. Сглаживателей пульсирующих токов в выпрямителях.
4. Фазосдвигающих элементов для электрических двигателей.

Применение конденсаторов в различных сферах основано именно на способности устройства накапливать электрический заряд. В более сложной электроаппаратуре эти устройства используются для бесперебойного поддержания определенного напряжения в разных накопителях данных.

Сопротивления конденсатора в зависимости от

Сопротивление конденсатора зависит от частоты подаваемого на него напряжения и показателя емкости.

Частоты и сдвига фаз

Устройство накопления зарядов одинаковой емкости на разных частотах оказывает различный уровень сопротивления. Оно растет или уменьшается.

При повышении частоты входного напряжения сопротивление (его также называют емкостным) уменьшается.

На низких частотах имеется в наличии сдвиг по фазе входного напряжения и напряжения на нагрузке.

С увеличением частоты сдвиг по фазе уменьшается.

При достижении частоты определенного уровня фазовый сдвиг стремиться к нулю.

Хс = 1/ωС,

где ω — круговая частота, равная произведению 2πf,

С—емкость цепи в фарадах.

Номинала конденсатора

Емкость конденсатора влияет на процесс зарядки и разрядки при прохождении через него переменного тока.

Устройство с меньшей емкостью будет быстрее отдавать заряд и вновь заряжаться.

Сопротивление переменному току будет выше, чем при медленной зарядке и разрядке.

Отсюда вывод: емкостное сопротивление находится в обратной зависимости от номинала конденсатора.

Время, необходимое для зарядки конденсатора

В идеальных условиях, когда источник напряжения мощный, нет препятствий потоку электричества, конденсатор безупречен, время зарядки конденсатора будет равно 0.

На практике же на каждом участке цепи существует явное (резисторы) или неявное (провода, источник напряжения и т.п.) сопротивление. В этом случае время заряда конденсатора будет зависеть от сопротивления во всей цепи и его емкости.

В самом начале заряда на обкладках накопителя много свободного места, напряжение равно нулю. Начальный ток в этот момент максимален. По мере заполнения конденсатора заряженными частицами их поток постепенно снижается, U растет все медленнее. Когда не останется свободного места на обкладках, ток прекратится, напряжение станет максимальным и равным таковому источника.

Экспонента увеличения энергии в конденсаторе изображена на рисунке. Сама формула зависимости нарастания напряжения от времени заряда имеет следующий вид:

U=Uc*[1-e(-t/τ)]

где Uс – электродвижущая сила источника, t – время заряда, τ – постоянная времени, равная R*C (R – сопротивление).

За время τ зарядка конденсатора дойдет до (1 – 1/e)*100% ≈ 63% от U.

За 3τ – до (1 – 1/e3)*100% ≈ 95% от U.

За 5τ – до (1 – 1/e5)*100% ≈ 99% от U.

Время заряда конденсатора точно до уровня напряжения источника длится бесконечно долго.

Из вышеприведенной формулы вычисления напряжения можно вывести расчет времени зарядки накопителя до определенных показателей:

t = – ln (1 – U/Uc) * RC

Зарядка конденсатора от источника постоянной ЭДС

Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.

Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна ε

(Рис. 145). Полное электрическое соединение цепи (включающее и внутренне сопротивление источника) обозначим R . При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе (~U_C = frac{q}{C}) и резисторе (U_R = IR) равна ЭДС источника (varepsilon = U_C + U_R), что приводит к уравнению

(~IR = varepsilon — frac{q}{C}) . (1)

В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи (~I = frac{Delta q}{Delta t}), что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени

(~R frac{Delta q}{Delta t} = varepsilon — frac{q}{C}) . (2)

Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин

(~Delta varepsilon = Delta (IR) + Delta left (frac{q}{C} right )) .

Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t

и ( t + Δ t ), а затем из второго уравнения вычесть первое. Так как ЭДС источника постоянна, то ее изменение равно нулю Δ ε = 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Δ , поэтому полученное уравнение приобретает вид

(~R Delta I = — frac{1}{C} Delta q) .

Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда)

Будет интересно➡ Автоматические выключатели

(~frac{Delta I}{Delta t} = -frac{1}{RC} I) . (3)

Математическая смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I

0 = I(0).

С уравнениями такого типа мы познакомились в «математическом отступлении», поэтому здесь его анализ проведем кратко.

В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна (~I_0 = Delta left (frac{Delta q}{Delta t} right )_0 = frac{varepsilon}{R}).

Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения (~overline{q} = Cvarepsilon) и ток в цепи прекратится.

Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае

(~tau = frac{overline{q}}{I_0} = RC) . (4)

Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату.

Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда.

Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса.

Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора

Рассмотрим теперь превращения различных форм энергии в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника.

На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q

, то сторонние силы совершили при этом работу A 0 = qε , при этом энергия конденсатора стала равной (~W = frac{q2}{2C} = frac{q varepsilon}{2}) , что в два раза меньше работы совершенной источником.

Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энергии источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки Δt

i ( i = 1,2,3…). Перепишем уравнение (1) в виде

(~varepsilon = IR + frac{q}{C}) , (5)

и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Δt

i, Δ q i = I iΔ t i . В результате получим

(~varepsilon Delta q_i = I_i R Delta q_i + frac{q_i}{C} Delta q_i) . (6)

Здесь обозначено q

i — заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл:[~varepsilon Delta q_i = delta A] — работа сторонних сил по перемещению порции заряда Δ q i;[~frac{q_i}{C} Delta q_i = Delta W_C] — увеличение энергии конденсатора при увеличении его заряда на Δ q i;[~I_i R Delta q_i = I2_i R Delta t_i = delta Q] — количество теплоты, выделившееся на резисторе, при протеканиипорции заряда Δ q i.

Таким образом, закон сохранения энергии, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки.

Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим:[~sum_i varepsilon Delta q_i = varepsilon overline{q} = A] — полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора;[~sum_i frac{q_i}{C} Delta q_i = frac{overline{q2}}{2C} = frac{varepsilon overline{q}}{2} = frac{C varepsilon2}{2}] — энергия заряженного конденсатора;

наконец, (~sum_i I_i R Delta q_i = sum_i I2_i R Delta t_i) — количество выделившейся на резисторе теплоты.

Принимая во внимание уравнение (3) и формулы из «математического отступления», последнюю сумму можно выразить в виде

(~Q = R sum_i I2_i Delta t_i = R frac{1}{2} I2_0 tau = R frac{1}{2} left ( frac{varepsilon}{R} right )2 RC = frac{C varepsilon2}{2}) . (6)

Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе (U_R = IR) от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии.

За малый промежуток времени через резистор протечет малый заряд Δq

i, при этом выделится количество теплоты (~delta Q_i = I_i R Delta q_i), которое численно равно площади узкой полоски, выделенной на рисунке.

Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости U

R( q ), то есть

Последовательное и параллельное соединение конденсаторов

Наиболее популярным типом соединения конденсаторов является параллельное. При этом подключении электроемкость повышается, а напряжение остается исходным.

К одной точке может подключаться несколько конденсаторов.

Так как электрическая емкость конденсаторов равна площади обкладок, общая емкость при таком виде соединения пропорциональна сумме емкостей всех конденсаторов в цепи.

Собщ.= C1+C2.

При последовательном соединении конденсаторов общая емкость снижается, а напряжение работы конденсатора возрастает.

Конденсаторы подключены так, что только первый и последний имеют доступ к источнику ЭДС/тока одной из своих пластин. Заряд одинаковый на всех пластинах, но наружные получают заряд от источника, а внутренние образуются благодаря разделению зарядов ранее нейтрализовавших друг друга. Емкость последовательного соединения двух конденсаторов мы можем вычислить по формуле

Собщ.= С1*С2/ C1+C2.

Применение конденсаторов

Конденсатор есть в каждом современном устройстве. Разберем два самых наглядных примера.

Пример раз — вспышка

Без конденсатора вспышка в фотоаппарате работала бы не так, как мы привыкли, а с большими задержками, и к тому же быстро разряжала бы аккумулятор. Конденсатор в этом случае работает как батарейка. Он накапливает заряд от аккумулятора и хранит его до востребования. Когда нам нужна вспышка, конденсатор разряжается, чтобы она сработала и вылетела птичка.

Формулы для вычисления

Измерения емкости осуществляется по специально выведенной формуле. Электрическая емкость (С) — это отношение сообщенного заряда (Q) к образующему в результате этого потенциалу (U). Формулу, которую используют, чтобы измерить емкость, выглядит следующим образом: C=Q/V . Единицей измерения служит фарада, которая обозначается буквой Ф. Емкость величиной 1 фарада будет хранить заряд q = 1 кулон при напряжении на обкладках U =1 Вольт. Так как конденсаторы имеют разные виды, формулы также используются разные.

Посредством математических выражений

Математическое выражение для определения емкости конденсатора С = q*U в единицах измерения в системе СИ каждой из входящих в формулу физических величин определяет значение 1 фарады.

Как зависит емкость от среды диэлектрика

Влияние изолятора на емкость конденсатора зависит от проводящих свойств вещества внутри этой прокладки. Способность межпластинного проводника на изоляцию называют диэлектрической проницаемостью. С учетом характеристик диэлектрика формула емкости плоского устройства станет: С = є0є S/d, где под буквой є стоит значение диэлектрической проницаемости изолятора, а є0 — постоянная величина равная диэлектрической проницаемости вакуума (воздуха).

На практике применяется коэффициент, обозначающий во сколько раз применяемый диэлектрик уменьшает электрическое поле по сравнению с воздухом.

Таблица:

Единицы измерения

Физическая величина, определяемая отношением заряда q одной из пластин конденсатора к напряжению между обкладками конденсатора, называется электроемкостью конденсатора:

При неизменном расположении пластин электроемкость конденсатора является постоянной величиной при любом заряде на пластинах. Единица электроемкости в международной системе – фарад (Ф). Электроемкостью 1 Ф обладает такой конденсатор, напряжение между обкладками которого равно 1 В при сообщении обкладкам разноименных зарядов по 1 Кл. . В практике широко используются дольные единицы электроемкости – микрофарад (мкФ), нанофарад (нФ) и пикофарад (пФ):

• 1 мкФ = 10-6Ф;
• 1 нФ = 10-9Ф;
• 1 пФ = 10-12Ф.

Электроемкость конденсатора прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между обкладками. При введении диэлектрика между обкладками конденсатора его электроемкость увеличивается в e раз. Если двум изолированным друг от друга проводникам сообщить заряды q1 и q2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников.

Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением и обозначают буквой U. Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q1 = – q2 = q. В этом случае можно ввести понятие электрической емкости.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними. Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства.

Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками. Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.

Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами (рисунок 1); однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния.

В целом ряде задач можно приближенно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками (рисунок 2). Но в других задачах пренебрежение полем рассеяния может привести к грубым ошибкам, так как при этом нарушается потенциальный характер электрического поля.

Будет интересно➡ Что такое электрическое поле: объяснение простыми словам

Согласно принципу суперпозиции, напряженность поля, создаваемого обеими пластинами, равна сумме напряженностей и полей каждой из пластин. Вне пластин вектора и направлены в разные стороны, и поэтому E = 0. Поверхностная плотность σ заряда пластин равна q/S, где q – заряд, а S – площадь каждой пластины. Разность потенциалов Δφ между пластинами в однородном электрическом поле равна Ed, где d – расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы.

Электроемкость – характеристика проводника, количественная мера его способности удерживать электрический заряд. В электростатическом поле все точки поверхности проводника имеют один и тот же потенциал.

Потенциал φ (отсчитываемый от нулевого уровня на бесконечности) пропорционален заряду q проводника, т.е. отношение q к φ не зависит от q. Это позволяет ввести понятие электроемкости. С уединенного проводника, которая равна отношению заряда проводника к потенциалу:

С = q/ φ

Таким образом, чем больше электроемкость, тем больший заряд может накопить проводник при данном φ. Электроемкость определяется геометрическими размерами проводника, его формой и электрическими свойства окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. В частности, электроемкость проводящего шара в вакууме равна его радиусу. Наличие вблизи проводника других тел изменяет его электроемкость, так как потенциал проводника зависит и от электрических полей, создаваемых зарядами, наведенными в окружающих телах вследствие электростатической индукции.

В системе ед. СГСЭ электроемкость измеряется в сантиметрах, в СИ – в фарадах: 1Ф = 9*1011 см. Понятие электроемкости относится также к системе проводников, в частности двух проводников, разделённых тонким слоем диэлектрика, – электрическому конденсатору. Электроемкость конденсатора (взаимная ёмкость его обкладок)

С = q/ (φ1 – φ2),

где q – заряд одной из обкладок (заряды обкладок по абсолютной величине равны), φ1 – φ2 – разность потенциалов между обкладками. Электроемкость конденсатора практически не зависит от наличия окружающих тел и может достигать очень большой величины при малых геометрических размерах конденсаторов.

Как измерить емкость

Существует некоторое количество способов измерения емкости конденсатора с помощью приборов и различных методик. В статье описывается использование мультиметра, осциллографа, тестера и мостовых измерителей.

Мультиметром

В начале, прежде чем начать измерение емкости конденсатора, его необходимо разрядить до полного исчезновения тока.

Как пример: сделать это с путем замыкания выводов отверткой.

Если пренебречь этим нюансом, то мультиметр может поломаться.

Измерить емкость с помощью мультиметра можно следующим образом: активируйте режим «Сх» и установите предел замера 2000 пФ, если он есть. На стандартном устройстве он равный 20 мкФ; Установите конденсатор в соответствующие гнезда в мультиметре или используйте щупы для подключения конденсатора. На экране прибора будет отображено значение емкости.

Осциллографом

Для измерения понадобиться кроме осциллографа собрать схему из тестируемого конденсатора, резистора и генератора синусоидальных колебаний.

Точки подключения осциллографа к схеме находятся до резистора и после конденсатора.

Частота колебаний генератора изменяется до получения на экране осциллографа одинаковых по амплитуде синусоидальных кривых. Это делается для точности измерений. Представьте как рассчитать емкость конденсатора с помощью амплитудных значений напряжений? Для этого требуется воспользоваться формулой UR/UC*2πfR подставив в нее измеренные значения. С его помощью также рассчитывается ток утечки конденсатора косвенным способом – через снижение напряжения на предварительно известном сопротивлении. Осциллограф способен вычислить емкость конденсаторов от 20 pF до 200 mkF.

Тестером не имеющим прямой функции

Для нахождения варианта, как определить емкость с помощью тестера без функции замера емкости, следует обратить внимание на формулу мгновенного значения тока во время его зарядки или разрядки i = С dU/dt.

Здесь дело в том, что кроме тестера и секундомера следует собрать схему с источником питания,

конденсатором и резистором с большим сопротивлением для увеличения длительности процесса зарядки или разрядки. После снятия всех показаний с тестера и секундомера можно, достаточно приближенно вычислить и узнать емкость. Зная, как определить емкость конденсатора современными приборами, будет несложно разобраться и с устройством со времен СССР. На экране происходит вывод не цифр, а отклонения стрелки, за которой важно внимательно следить. Измерение емкости осуществляется только на разряженном конденсаторе. Щупы выведите к контактам конденсатора, если он рабочий, то стрелка изначально отклонится, после чего по мере заряда займет исходную позицию. Скорость передвижения стрелки зависит от объема емкости. Если стрелка тестера не сдвинулась с места, либо эта величина минимальная или отклонилась и зависла в одном положении – это показатель неисправности конденсатора.

Мостовыми измерителями

Емкость конденсатора измеряется методом сравнения с эталонной емкостью. Для чего выполняется мостовая схема, где одно плечо работает с образцовым электрическим устройством, другое с тестируемым. Показания моста могут быть реализованы на цифровых носителях.

Номинальное напряжение

Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).

Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.

Маркировка конденсаторов

На корпусе каждого конденсатора имеется специальная маркировка – буква и цифра. По сравнению с резисторами, маркировка конденсатора, обозначающая емкость и код отклонения емкости, довольно-таки сложная и разнообразная. Иногда обозначения наносятся прописными буквами – MF (микрофарады), fd – фарады. Также на корпусе указаны положительные и отрицательные символы, помогающие определить полярность конденсатора.

Способы обозначения конденсатора

Единицей измерения емкости конденсатора является фарад, поэтому на корпусе элемента обязательно присутствует буква Ф или F:

• 1 миллифарад = 10-3 фарад = 1мФ;
• 1 микрофарад = 10-6 фарад = 1 мкФ;
• 1 нанофарад = 10-9 фарад = 1 нФ;
• 1 пикофарад = 10-12 фарад = 1 пФ.

Если на элементе не обозначен номинал, то целое значение свидетельствует о том, что емкость указана в пикофарадах. На корпусе емкость указывается с отклонением, если указана буква J – то диапазон отклонения менее 5%, буква М – 20%.

Код конденсаторов импортного производства

Устройства импортного производства, так же как и российские, имеют маркировку согласно международных стандартов. Данный нормативный документ предполагает нанесение кода из трех цифр. Первые две цифры обозначают емкость в пикофарадах. Третья цифра говорит о количестве нулей, например, если емкость будет меньше 1 пикофарады, цифра будет выглядеть как «0».

Кодовая для конденсаторов поверхностного монтажа

Маркировка электролитических SMD конденсаторов состоит из емкости и рабочего напряжения. Например,108V, где закодирована электроемкость 10 пф и рабочее напряжение 8 Вольт. Знак плюс находится рядом с полоской. Выделяют три основных способа кодировки: код из двух или трех знаков (буквы или цифры), которые указывают на рабочее напряжение и номинальную емкость. Показатели указываются буквой, а цифра является множителем; четыре знака, обозначающие напряжение и номинальную емкость. Первая буква – это рабочее напряжение, следующие символы – емкость в пикофарадах, последняя цифра – количество нулей;

если площадь корпуса большая, кода располагают на две строки. Верхняя строка – номинал емкости, нижняя – рабочее напряжение.

Неполярные конденсаторы

К неполярным конденсаторам относят конденсаторы, для которых неважна полярность. Такие конденсаторы обладают симметричностью. Обозначение неполярных конденсаторов на электросхемах выглядит вот так.

обозначение конденсатора на схеме

Конденсаторы переменной емкости

Эти виды конденсаторов имеют воздушный диэлектрик и могут менять свою емкость под действием внешней силы, например, такой как рука человека. Ниже на фото советские типы таких переменных конденсаторов.

переменные конденсаторы

Современные выглядят чуточку красивее

подстроечные конденсаторы

Переменный конденсатор от подстроечного отличается лишь тем, что переменный конденсатор крутят чаще, чем подстроечный. Подстроечный крутят раз в жизни)

На схемах обозначаются так.

переменный конденсатор обозначение на схеме

Слева -переменный, справа — подстроечный.

Пленочные конденсаторы

Пленочные конденсаторы являются самыми распространенными в большом семействе конденсаторов. Они названы так потому, что вместо диэлектрика здесь используется тонкая пленка, которая может состоять из полиэстера, полипропилена, поликарбоната, тефлона и много еще из чего. Такие конденсаторы идут от номинала 5 пФ и до 100 мкФ. Они могут быть сделаны по принципу бетерброда

А также по принципу рулета

Давайте рассмотрим К73-9 советский пленочный конденсатор.

к73-9 советский конденсатор

Что же у него внутри? Смотрим.

Как и ожидалось, рулончик из фольги с диэлектриком-пленкой

что внутри конденсатора

Керамические конденсаторы

Керамические конденсаторы — это конденсаторы, которые изготавливают из керамики или фарфора, которые покрывают серебром. Берут диск квадратной или круглой формы, напыляют с с двух сторон серебро, выводят выводы и вуаля! Конденсатор готов! То есть и есть самый простой плоский конденсатор, о котором мы говорили выше в этой статье.

Хотите получишь емкость больше? Не вопрос! Складываем диски в бутерброд и увеличиваем емкость

Выглядеть керамические конденсаторы могут вот так:

керамические конденсаторы

керамические каплевидные конденсаторы

SMD конденсаторы

SMD конденсаторы — это керамические конденсаторы, которые построены по принципу бутерброда.

строение SMD конденсатора

Они используются в микроэлектронике, так как обладают крошечными размерами и удобны в плане промышленного производства с помощью роботов, которые автоматически расставляют SMD компоненты на плату.Такой тип конденсаторов вы без труда можете найти на платах своих мобильных телефонов, на материнских платах компьютеров, а также в современных гаджетах.

Гауссовский обобщенный закон

Описывая кулоновскую силу между точечными зарядами в диэлектрике, электрическая проницаемость вакуума умножалась на диэлектрическую проницаемость и вместо ε мы использовали произведение ε ε. Мы можем обобщить эту процедуру и применить ее к закону Гаусса, где центром, через который проникает поле, является не вакуум, а диэлектрик. Тогда мы знаем закон Гаусса

мы сможем написать в форме

мы получим окончательную форму обобщенного закона Гаусса

Закон Гаусса в таком виде применяется в вакууме, где ε = 1, и в диэлектриках. Заряд Q в этом уравнении, как и прежде, представляет собой результирующий заряд, содержащийся внутри замкнутой поверхности, после чего происходит интегрирование.

В конденсаторе с диэлектриком результирующий заряд представляет собой разницу между нагрузкой, накопленной на крышке q1 = σA, и поляризационным зарядом (с противоположным знаком), индуцированным в диэлектрике поверхностного слоя q2 = -σ и A. Если мы используем закон Гаусса для этой структуры, то мы предполагаем, что заряды они накапливаются на соседних поверхностях крышки и диэлектрика, и это поле не выходит за пределы крышек конденсатора. Естественным выбором гауссовой поверхности, после которой мы интегрируем поток, является прямоугольная призма или поверхность цилиндра. Основание прямоугольной призмы А параллельно поверхности крышки. Одна база находится снаружи крышки (там, где нет поля), а другая находится внутри диэлектрика.

Закон Гаусса в представленной выше форме является одним из четырех уравнений Максвелла, описывающих все электрические, магнитные и оптические явления. Уравнения Максвелла являются фундаментальными законами электродинамики, и ни одно из них не может быть выведено из более простых законов. Если бы существовали еще более фундаментальные права, они, безусловно, были бы представлены здесь. Эти уравнения являются результатом творческого вдохновения, просвещения их создателей Гаусса, Фарадея и Ампера. Максвелл представил им гениальную концепцию «тока смещения», о которой мы поговорим чуть позже, которая позволила унифицировать структуру этих уравнений и распространить их на случай электромагнитных и, следовательно, световых волн.