Что такое активное сопротивление в цепи переменного тока

Переменный ток — основной источник бытового и промышленного электроснабжения. При подаче напряжения на потребителях возникает сопротивление. Статья даст подробное разъяснение, что такое активное сопротивление в цепи переменного тока.

Дополнительно будет дана формула расчета этого значения, описаны разновидности, условия для идеальной цепи и основные факторы, влияющие на увеличение этих значений.

Переменный ток

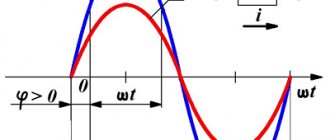
Для того чтобы понять, что такое активное сопротивление, необходимо разобраться в самом явлении переменного тока. Переменным является такой тип тока, который непрерывно изменяет направление своего протекания. Во время протекания потенциалы переменного тока постоянно изменяются. Это происходит благодаря работе генератора, а точнее за счет взаимодействия магнитного поля с медной обмоткой. Движение хорошо прослеживается при помощи осциллографа. Своей формой оно напоминает синусоиду.

Роль переменного тока сложно переоценить. Главное его достоинство заключается в простоте передачи от источника к потребителю, возможность занижать или увеличивать напряжение при помощи трансформаторов. Также, переменные электрические токи можно доставлять потребителю с гораздо меньшими затратами.

Треугольник сопротивлений

Схема цепи, подключенной к переменному току, имеет полное сопротивление, которое можно определить в виде суммы квадратов реактивного и активного сопротивлений.

Если изобразить это выражение в виде графика, то получится треугольник сопротивлений. Он образуется, если рассчитать последовательную цепь всех трех видов сопротивлений.

По этому треугольному графику можно увидеть, что катеты представляют собой активное и реактивное сопротивление, а гипотенуза является полным сопротивлением.

Сопротивление

Сопротивлением является способность проводника замедлять прохождение заряженных частиц через свою структуру. На эту способность влияет материал проводника, его толщина и длина. Единицей измерения электрического сопротивления является 1 Ом.

Расчет производится при пропускании через проводник напряжения в один вольт и силой тока равной одному амперу. В электрических схемах данный параметр обозначается буквой «R».

Активное сопротивление

Переменный ток доставляется потребителю с целью его преобразования в иные виды энергии, например, тепло и свет. В бытовых сетях преобладает использование однофазного переменного тока. При подключении потребителя создается активное сопротивление.

Простые цепи переменного тока с активным сопротивлением включает в себя генератор тока и идеальный резистор. При этом должны соблюдаться необходимые условия для идеальной цепи:

1. Активное сопротивление не должно равняться нулю, обязательное условие.
2. Емкость и индуктивность цепи должны быть равны нулю.

Также, для идеального активного сопротивления должны соблюдаться следующие условия:

1. Соблюдаются закон Ома для мгновенных, среднеквадратичных и амплитудных параметров цепи.
2. Значение полностью независимо от амплитудных колебаний.
3. Между током и напряжением отсутствует сдвиг фаз.
4. Элемент, находящийся под напряжением, выделяет долю тепловой энергии, то есть нагревается.

Все эти условия позволяют электрическим приборам работать в пределах точно установленных параметров с максимальным КПД. Любое изменение может быть причиной отсутствия надежного контактного соединения или неисправностью самого потребителя.

Для того чтобы рассчитать величину активного сопротивления в цепи, необходимо знать величину напряжения и силы тока. Для расчета используется формула: R=U/I. Формула состоит из следующих значений:

1. «R» — сопротивление, Ом;
2. «U» — величина напряжения, вольт;
3. «I» — величина силы тока, ампер.

Далее можно сделать простой расчет. В качестве потребителя выступает электрическая печь, включенная в цепь однофазного переменного тока:

1. Напряжение цепи 240 вольт.
2. При замере силы тока получено значение 4 ампера.
3. R= 240/4=60 Ом.

Расчетная величина активного сопротивления — это не окончательное значение. На нее влияет прежде всего сечение проводов включенных в цепь, схема взаимодействия между цепями емкостных и полупроводниковых элементов.

Активное значение цепи также вызывает безвозвратную потерю первоначальной электрической энергии, а так же приводит к снижению мощности.

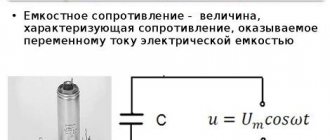
Цепь с емкостным сопротивлением.

Определим характер переменного тока «I

» в цепи с конденсатором, к которой приложено переменное напряжение
U = Um sint
.

Мгновенные значения заряда «q»

на пластинах конденсатора

q = cU = cUm sin
t.
Дифференцируем

где Im =
cUm
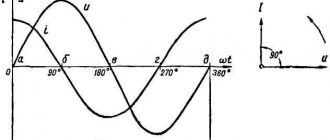
. Это уравнение показывает, что ток в цепи, подобно напряжению, имеет синусоидальный характер (смотри рисунок), причем упреждает напряжение по фазе на угол.Сопоставляя максимальное значение тока
Im =cUm
с формулой закона Ома, видим, что в цепи с емкостью значение сопротивления имеет величина , которая обозначается
Xc.
Величина называется емкостным сопротивлением цепи и измеряется в Омах, если
с
— в Фарадах и

— в Герцах. Физический смысл емкостного сопротивления можно объяснить так: ток «
I
» в цепи конденсатора пропорционален заряду «
q
» и частоте «

» смены процессов заряда и разряда конденсатора. Заряд «
q
» при данном приложенном напряжении «
U
» пропорционален емкости «
с
» конденсатора, а
= 2
. Поэтому ток «
I
» в цепи пропорционален произведению «
c
«, которое, следовательно, имеет значение проводимости цепи. Величина, ей обратная, то есть , имеет значение сопротивления цепи.В цепи, содержащей емкость и активное сопротивление, угол сдвига фазы тока будет меньше и в зависимости от соотношения между ними может иметь значения от 0 до 90.В чисто емкостном сопротивлении потерь энергии не происходит, в связи с чем оно называется реактивным.

34. Полное сопротивление цепи переменного эл.тока. Импеданс. .

Рассм. цепь, состю из последю соед-ных резистора R, катушки индук-тивности
L
и конденсатора
С.
Если на нее подать перемен. напряж-е , то ток в цепи будет изм-ся по закону: ,где- разность фаз напр-я и силы тока. Такая цепь им. как актив., так и реактивное сопр-я. => ее сопр-е наз. импедансом и обо­значают
Z.Импеданс
равен отношению амплитуд. значе­ния переем. напр-я на концах цепи к ам­плитуд. Знач-ю силы тока в ней:

Элементы(R,L,С)

полной цепи перем. тока на рис. соединены
последо-вательно.
=> по ним про­текает одинак. ток, а напрсклад-ся из напр-ний на отдел. участках цепи:Для сложения напр-ний исп. след. графи­ч. прием. На вектор.диаграмме отклад-ся
как век­торы
все 3 ампл-ды напр-ний Тогда сумма этих векторов дает вектор напряж-я в цепи. Вел-на и направл-е вектора дают амплитуду напр-ния в сети и фазовый угол между током и напряжением. Из рис. по т. Пифагора имеем: Подставляя выражения этих амплитуд из и учит. закон Ома, находим:Дальше пол. выр-е для определения импеданса:

Активная емкость

В простой схеме величина активного значения также зависит от активной емкости. Для идеальной емкости — в схеме под переменным напряжением должен находится конденсатор. Идеальный конденсатор обозначается буквой «С».

Для получения идеальной цепи с активной емкостью, должны соблюдаться следующие условия:

1. Активная индуктивность и сопротивление должны быть равны 0.
2. Емкость самого конденсатора в цепи должна быть больше 0.

При данных условиях электрическая цепь приобретает следующие особенности:

1. Закон Ома соблюдается без малейших отклонений.
2. На переменный ток оказывается емкостное сопротивление «X».
3. Прослеживается нелинейное уменьшение емкости при повышении частоты колебаний.
4. Между напряжением и током происходит сдвиг по фазе до величины 90 градусов.
5. Емкость цепи непостоянна. Причина кроется в периодическом накоплении и отдаче энергии.

Цепь переменного тока с активным емкостным сопротивлением может дополняться индуктивностью. Для создания индуктивности, в цепь включается катушка индуктивности. Катушка также добавляет свою долю сопротивления в общую цепь. При таком подключении в схеме появляется индуктивное сопротивление. Оба элемента: катушка и конденсатор, не являются конечными потребителями энергии. Эти элементы не находятся под постоянным напряжением, их работа строится на накоплении и отдаче тока в цепь.

Реактивное сопротивление конденсатора

Как мы увидели с прошлого опыта, с увеличением частоты растет сила тока! Кстати, у резистора не росла. То есть получается в данном случае из закона Ома, что сопротивление конденсатора зависит от частоты! Да, все так оно и есть. Но называется оно не просто сопротивлением, а реактивным сопротивлением и вычисляется по формуле:

где

Хс — реактивное сопротивление конденсатора, Ом

П — постоянная и приблизительно равна 3,14

F — частота, Гц

С — емкость конденсатора, Фарад

Мощность

При наличии активного сопротивления, значительно снижается мощность этой цепи. Это значение зависит от скорости снижения напряжения и преобразования электрической энергии. В электрической схеме мощность обозначается буквой «P».

Для того чтобы добиться минимального снижения средней и мгновенной мощностей, которые образуются в момент появления активного сопротивления, снижения напряжения и преобразования энергий, необходимо чтобы простейшие цепи состояли из идеальных элементов с высокой электрической проводимостью.

Зависимость

Величина активного сопротивления во многом зависит от диаметра проводников. При подаче высокочастотных токов, сопротивление проводника может быть снижено, только если его поверхностный слой намного тоньше основного. Для того чтобы добиться идеального сечения, этот слой должен состоять из материала с очень высокой проводимостью, например, золота или серебра. Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.

Так же присутствуют следующие эффекты: потери утечки и диэлектрические потери. Оба эффекта связаны с наличием конденсатора в цепи. Диэлектрические потери возникают за счет увеличения температуры диэлектрика внутри конденсатора. Потеря утечки возникает в следствии доли пробоя изолятор конденсатора.

Гистерезис. Это тоже тип потери энергии переменного тока. Такая потеря возникает при формировании магнитного поля вокруг предметов из металла. Электромагнитное воздействие приводит к нагреванию металла, а значит преобразованию энергии.

Последним фактором утечки является радиоизлучение. Радиоволны появляются по причине сильного магнитного поля и его взаимодействия с металлами цепи. Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.

Решая это уравнение относительно f , находим

(3.40)
При резонансе напряжений частота источника равна собственной частоте колебаний контура.

Выражение (3.40) является формулой Томсона, определяющей за­висимость собственной частоты колебаний контура

, от параметровL

и
С
. Следует вспомнить, что если конденсатор контура зарядить от ис­точника постоянного тока, а затем замкнуть его на индуктивную ка­тушку, то в контуре возникнет переменный ток частоты

. Вследствие потерь колебания в контуре будут затухать, причем время затухания зависит от величины потерь.

Рис. 55

Резонансу напряжений соответствует векторная диаграмма, при­веденная на рис.55. На основании этой диаграммы и закона Ома для цепи с r,
L
и
С
сформулируем признаки резонанса напряжений:

а) сопротивление всей цепи

мини­мальное и чисто активное;

б) ток цепи совпадает по фазе с напряже­нием источника и достигает максимального значения;

Рис. 56 Рис. 57

в) напряжение на индуктивной катушке равно напряжению на емкости и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.

Физически это объясняется тем, что напряжение источника при резонансе идет только на покрытие потерь в контуре. Напряже­ние на индуктивности и емкости обусловлено накопленной в них энергией, величина которой тем больше, чем меньше потери в цепи.

Количествен­но указанное явление характеризуется добротностью кон­тура
Q
, которая представляет собой отношение напряжения на ка­тушке или емкости к напряжению на зажимах цепи при резонансе;

. (3.41)
При резонансе

Величина

называется волновым сопротивлением контура. Таким образом,

(3.42)

Способность колебательного контура выделять токи резонансных частот и ослаблять токи других частот характеризуется резонансной кривой (рис. 56).

Резонансная кривая показывает зависимость действующего значе­ния тока в контуре от частоты источника при неизменной собственной частоте контура.

Эта зависимость определяется законом Ома для цепи с r,L

и
С
. Действительно,
I =Uz
, где

(3.43)

На рис. 57 показана зависимость реактивного сопротивления

от частоты источника. Анализ этого графика и выражения (3.43) показывает, что при низких и высоких частотах реактивное со­противление велико и ток в контуре мал. При частотах, близких

реактивное сопротивление мало и ток контура велик. При этом, чем больше добротность контураQ

, тем острее резонансная кривая кон­тура.

Замер

Измерение сопротивления осуществляется следующими способами:

1. Вольтметр и амперметр. С помощью этих приборов измеряются величины силы тока и напряжения, а после производится расчет по описанной выше формуле.
2. Логометром. Это прибор для измерения сопротивления под высоким напряжением и большой частотой. Его главное преимущество в сильном исключении зависимостей и погрешностей.
3. Омметр. Прибор используется только для измерения по типу усилителя сигнала. При использовании омметра учитывается высокая погрешность, которая может достигать 5 %. Обычные омметры электронного типа не подходят для замера активного сопротивления.

Курс лекций по физике Электротехника

Цепь с активным сопротивлением и емкостью

1. Векторная диаграмма тока и напряжений. В § 11.4 рассмотрена цепь с емкостью (идеальный конденсатор). В действительности любой конденсатор обладает потерями, т. е. активной мощностью Р. Поэтому реальный конденсатор можно представить схемой последовательного соединения активного сопротивления г и емкостного сопротивления хс (рис. 12.5). Сопротивление г определяется мощностью потерь: г = P/I2. Напряжение цепи и в любой момент времени состоит из двух слагаемых: u=ua+uc. Активное напряжение иа совпадает по фазе с током в цепи i, а емкостное uС отстает по фазе от тока на 90°. Действующие значения слагаемых напряжения: Ua = Ir, UC = IxC = I/(С). Для определения действующего значения напряжения U построим векторную диаграмму. Построение диаграммы (рис. 12.6, а) начнем с вектора тока I, отложив его горизонталь но.

Вектор активного падения напряжения Ua отложим по н равлению вектора тока I, а вектор емкостного падения напряжения Uc повернем относительно вектора тока на 90° по ходу часовой стрелки. Сложим векторы напряжений Ua и Uc, получим вектор напряжения U. Векторы напряжений Ua, Uc и U образуют прямоугольный треугольник. Из векторной диаграммы видно, что напряжение на зажимах цепи отстает по фазе от тока на угол ф. Абсолютную величину этого угла можно определить из выражения cosф= Ua/U.

2. Треугольники сопротивлений и мощностей. Все стороны треугольника напряжений уменьшим в I раз. В результате получим треугольник сопротивлений (рис. 12.6, б). Иэ этого треугольника следует, что полное сопротивление рассматриваемой цепи

Значит, ток

Полученное выражение представляет собой закон Ома. При увеличении сторон треугольника напряжений (рис. 12.6, а) в I раз получим подобный треугольник мощностей (рис. 12.6, в). Мощности цепи: активная Р = UaI = I2r = UI cos ф, реактивная QC == UCI = I2xC = UIsin ф, полная S= UI =.

Цепь с активным сопротивлением, индуктивностью и емкостью

1. Векторная диаграмма тока и напряжений. Если в неразветвленной цепи с активным сопротивлением г, индуктивностью L и емкостью С (рис. 12.7) протекает синусоидный ток i=Imsint, то мгновенное значение приложенного к цепи напряжения и = ua + uL+uc. Напряжение на активном сопротивлении иа совпадает по фазе с током в цепи i, напряжение на индуктивности uL опережает ток на 90°, а напряжение на емкости ис отстает от тока на 90°. Действующие значения напряжений на участках цепи: Ua=Ir; UL = IxL; Uc=Ixc. Действующее значение напряжения на зажимах цепи получим методом векторного сложения: U = Ua+UL+Uc. Построим векторную диаграмму тока и напряжений. Сначала отложим вектор тока I (рис. 12.8,а). Вектор падения напряжения в активном сопротивлении Ua совместим с вектором тока I, век тор индуктивного падения UL отложим вверх под углом 90°, а вектор емкостного падения напряжения Uc — вниз под углом 90° к вектору тока I. Сложив векторы напряжений Ua, Ul и UC, получим вектор напряжения U, приложенного ко всей цепи. Векторная диаграмма построена для случая, когда xL>xC и цепь имеет активно-индуктивный характер. При этом условии UL>Uc, а напряжение U опережает по фазе ток I на угол ф. Если xc>xl, to Uc>Ul и цепь имеет активно-емкостный характер. При этом напряжение U (рис. 12.9) отстает по фазе от тока I на угол ф. При равенстве реактивных сопротивлений (xl=xc) Ul = Uc (рис. 12.10). При этом напряжение U совпадает по фазе с током I (ф=0) и цепь носит активный характер. Этот режим в рассматриваемой цепи называется резонансом напряжений.

2. Треугольники сопротивлений и мощностей. Рассмотрим треугольник напряжений на рис. 12.8,я. Один катет этого треугольника выражает активное напряжение Ua другой — реактивное напряжение цепи UL–UC, а гипотеза — полное напряжение U. Разделив стороны треугольника напряжений на ток I, получим треугольник сопротивлений (см. рис. 12.8,6), из которого следует, что полное сопротивление цепи z =. Поэтому ток в цепи

Если все стороны треугольника напряжений (см. рис. 12.8, а) умножить на ток I, то получим треугольник мощностей (см. рис. 12.8, в). Мощности: активная Р = UaI =I2г = UIсоs ф,

где cos ф = Uа/U = r/z; реактивная Q = (UL— UC)I = I2·(xL—xc)= UIsin ф; полная S = UI =.

Общий случай неразветвленной цепи

1. Векторная диаграмма тока и напряжений. На рис. 12.12 показана схема неразветвленной цепи, участки которой обладают активными и реактивными сопротивлениями. На векторной диаграмме (рис. 12.13, а) отложены векторы активных напряжений Ua1, Ua2, Ua3, совпадающих по фазе с током, индуктивных — UL1 и UL2, опережающих ток по фазе на 90°, и емкостных — UC1 и UC2, отстающих от тока по фазе на 90°. Сумма всех векторов напряжений равна вектору напряжения U на зажимах цепи. На векторной диаграмме (рис. 12.14) векторы напряжений построены в той же последовательности, в которой соединены соответствующие элементы цепи.

2. Треугольники сопротивлений и мощностей. Рассмотрим векторную диаграмму на рис. 12.13, а. Первый катет полученного треугольника напряжений равен арифметической сумме активных напряжений (Ua1+Ua2+Ua3), второй — алгебраической сумме реактивных напряжений (UL1+Vl2— UC1 — UC2), а гипотенуза — напряжению U на зажимах цепи. Уменьшив все стороны этого треугольника в I раз, получим треугольник сопротивлений (рис. 12.13,, б), из которого следует, что полное сопротивление цепи z =. В общем виде

Ток в цепи

Увеличив каждую из сторон треугольника напряжений в I раз, получим треугольник мощностей (рис. 12.13, в). Мощности цепи: активная Р = I2(г1 + г2 + г3) = UI cos ф, где cos ф = (г1 + г2 + г3)/z или cos ф=∑r/z; реактивная Q = I2(хL1 +хL2 — хС1 — хС2) = UIsin ф, где sin ф = (xL1 +xL2 — xL3 — xC2)/z или sin ф=(∑xL —∑хС)/z; полная S= UI = .