Для использования в других целях см. Оборотов в минуту (значения).
«rpm» перенаправляется сюда. Для использования в других целях см. RPM (значения).
| Эта статья нужны дополнительные цитаты для проверка . Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален. |
| Число оборотов в минуту | |
| Единица | Скорость вращения |
| Символ | об / мин или об / мин |
| Конверсии | |
| 1 об / мин в … | … равно … |
| Угловая скорость СИ | 2π/60 рад / с ≈ 0,1047198 рад / с |
| Частота SI | 1/60 Гц ≈ 0,01666667 Гц |
| Производная частота вращения SI | 1/60 s−1, 1/60/ с |
| Производная скорость вращения SI | 1 мин−1, 1 мин |
Число оборотов в минуту
(сокращенно
об / мин
,
Об / мин
,
об / мин
,
об / мин
, или с обозначением min−1) — количество повороты в одной минута. Это единица скорость вращения или частота из вращение вокруг фиксированной оси.
Вращательное движение (движение тела по окружности) | Формулы и расчеты онлайн
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если: перемещение s
— угловое перемещение (угол поворота)
φ
, скорость
u
— угловая скорость
ω
, ускорение
a
— угловое ускорение
α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно (рад)
.
Если φ
— угловое перемещение в радианах,
s
— длина дуги, заключенной между сторонами угла поворота,
r
— радиус, то по определению радиана
\[ φ = \frac{s}{r} \]
Соотношение между единицами угла
\[ \frac[-1.35]{φ_{рад}}{φ_{°}} = \frac[-1.2]{π}{180°} \]
| $ 1 рад = 57.3° $ | $ 1° = 17.45 мрад $ | $ 1´ = 291 мкрад $ |
Обратите внимание:
Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков (1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω
от
t
). Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ
от
t
) и график углового ускорения (зависимость
α
от
t
).
Число оборотов
Характеристикой всех видов вращения является число оборотов n
или равноценная ей характеристика — частота
f
. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
\[ [n] = [f] = \frac{Обороты}{Секунда} = \frac{(об)}{с} = \frac{1}{c} = Герц \]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если n
— число оборотов,
f
— частота,
T
— продолжительность одного оборота, период,
φ
— угловое перемещение,
N
— полное число оборотов,
t
— время, продолжительность вращения,
ω
— угловая частота, то
Период
\[ T = \frac{1}{f} = \frac{1}{n} \]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
\[ φ = 2 π N \]
Угловая скорость
Из формулы для одного оборота следует:
\[ ω = 2 π f = \frac{2π}{T} \]
Обратите внимание:
•
формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
•
вопреки своему названию число оборотов
n
— это не число, а физическая величина.
•
следует различать число оборотов
n
и полное число оборотов
N
.
В помощь студенту
Вращательное движение (движение тела по окружности) | стр. 421 |
www.fxyz.ru
Угол поворота и период обращения
Рассмотрим точку А на предмете, вращающимся вокруг своей оси. При обращении за какой-то период времени она изменит своё положение на линии окружности на определённый угол. Это угол поворота. Он измеряется в радианах, потому что за единицу берётся отрезок окружности, равный радиусу. Ещё одна величина измерения угла поворота – градус.
Когда в результате поворота точка А вернётся на своё прежнее место, значит, она совершила полный оборот. Если её движение повторится n-раз, то говорят о некотором количестве оборотов. Исходя из этого, можно рассматривать 1/2, 1/4 оборота и так далее. Яркий практический пример этому – путь, который проделывает фреза при фрезеровании детали, закреплённой в центре шпинделя станка.
Формула расчета частоты вращений
При проектировании оборудования необходимо знать число оборотов электродвигателя. Для расчёта частоты вращения есть специальные формулы, различные для двигателей переменного и постоянного напряжения.
Тахометр
Синхронные и асинхронные электромашины
Двигатели переменного напряжения есть трёх типов: синхронные, угловая скорость ротора которых совпадает с угловой частотой магнитного поля статора; асинхронные – в них вращение ротора отстаёт от вращения поля; коллекторные, конструкция и принцип действия которых аналогичны двигателям постоянного напряжения.
Синхронная скорость
Скорость вращения электромашины переменного тока зависит от угловой частоты магнитного поля статора. Эта скорость называется синхронной. В синхронных двигателях вал вращается с той же быстротой, что является преимуществом этих электромашин.
Для этого в роторе машин большой мощности есть обмотка, на которую подаётся постоянное напряжение, создающее магнитное поле. В устройствах малой мощности в ротор вставлены постоянные магниты, или есть явно выраженные полюса.
Скольжение
В асинхронных машинах число оборотов вала меньше синхронной угловой частоты. Эта разница называется скольжение «S». Благодаря скольжению в роторе наводится электрический ток, и вал вращается. Чем больше S, тем выше вращающий момент и меньше скорость. Однако при превышении скольжения выше определённой величины электродвигатель останавливается, начинает перегреваться и может выйти из строя. Частота вращения таких устройств рассчитывается по формуле на рисунке ниже, где:
- n – число оборотов в минуту,
- f – частота сети,
- p – число пар полюсов,
- s – скольжение.
Формула расчёта скорости асинхронного двигателя
Такие устройства есть двух типов:
- С короткозамкнутым ротором. Обмотка в нём отливается из алюминия в процессе изготовления;
- С фазным ротором. Обмотки выполнены из провода и подключаются к дополнительным сопротивлениям.
Регулировка частоты вращения
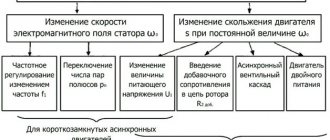
В процессе работы появляется необходимость регулировки числа оборотов электрических машин. Она осуществляется тремя способами:
- Увеличение добавочного сопротивления в цепи ротора электродвигателей с фазным ротором. При необходимости сильно понизить обороты допускается подключение не трёх, а двух сопротивлений;
- Подключение дополнительных сопротивлений в цепи статора. Применяется для запуска электрических машин большой мощности и для регулировки скорости маленьких электродвигателей. Например, число оборотов настольного вентилятора можно уменьшить, включив последовательно с ним лампу накаливания или конденсатор. Такой же результат даёт уменьшение питающего напряжения;
- Изменение частоты сети. Подходит для синхронных и асинхронных двигателей.
Внимание! Скорость вращения коллекторных электродвигателей, работающих от сети переменного тока, не зависит от частоты сети.
Двигатели постоянного тока
Кроме машин переменного напряжения есть электродвигатели, подключающиеся к сети постоянного тока. Число оборотов таких устройств рассчитывается по совершенно другим формулам.
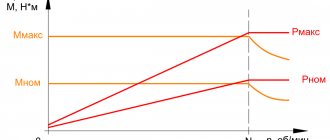
Номинальная скорость вращения
Число оборотов аппарата постоянного тока рассчитывается по формуле на рисунке ниже, где:
- n – число оборотов в минуту,
- U – напряжение сети,
- Rя и Iя – сопротивление и ток якоря,
- Ce – константа двигателя (зависит от типа электромашины),
- Ф – магнитное поле статора.
Эти данные соответствуют номинальным значениям параметров электромашины, напряжению на обмотке возбуждения и якоре или вращательному моменту на валу двигателя. Их изменение позволяет регулировать частоту вращения. Определить магнитный поток в реальном двигателе очень сложно, поэтому для расчетов пользуются силой тока, протекающего через обмотку возбуждения или напряжения на якоре.
Формула расчёта числа оборотов двигателя постоянного тока
Число оборотов коллекторных электродвигателей переменного тока можно найти по той же формуле.
Регулировка скорости
Регулировка скорости электродвигателя, работающего от сети постоянного тока, возможна в широких пределах. Она возможна в двух диапазонах:
- Вверх от номинальной. Для этого уменьшается магнитный поток при помощи добавочных сопротивлений или регулятора напряжения;
- Вниз от номинальной. Для этого необходимо уменьшить напряжение на якоре электромотора или включить последовательно с ним сопротивление. Кроме снижения числа оборотов это делается при запуске электродвигателя.
Знание того, по каким формулам вычисляется скорость вращения электродвигателя, необходимо при проектировании и наладке оборудования.
Видео
Оцените статью:
elquanta.ru
Примеры
- На граммофонных пластинках скорость вращения задается в об/мин: например, стандартные скорости вращения 16 + 2 ⁄ 3 , 33 + 1 ⁄ 3 , 45 или 78 об/мин ( 5 ⁄ 18 , 5 ⁄ 9 , 3 ⁄ 4 , или 1,3 об/с соответственно).
- Новые ультразвуковые бор-машины имеют скорость вращения до 800 000 об/мин (13 300 об/с).
- Секундная стрелка часов вращается с частотой 1 об/мин.
- Проигрыватели звуковых компакт-дисков производят чтение со скоростью 150 кБ/с и, следовательно, при скорости вращения диска у внутреннего края примерно 500 об / мин (8 об/с) и 200 об / мин (3,5 об/с) на внешней границе. Приводы компакт дисков имеют скорость вращения, кратную этим цифрам, даже если используется переменная скорость чтения.
- DVD -проигрыватели также обычно читают диски с постоянной линейной скоростью. Скорость вращения изменяется от 1 530 об/мин (25,5 об/с), при чтении у внутреннего края, и 630 об/мин (10,5 об/с) на внешней стороне диска. DVD-приводы также работают на скорости, кратной вышеназванным цифрам.
- Барабан стиральной машины может вращаться со скоростью от 500 до 2000 об/мин (8-33 об/с) во время отжима.
- Турбина генератора вращается со скоростью 3000 об/мин (50 об/с) или 3600 об/мин (60 об/с), в зависимости от страны (см. Переменный ток#Стандарты частоты). Вал генератора гидроэлектростанции может вращается медленнее: до 2 об/с (при этом частота сети 50 Гц получается за счет наличия большего количества полюсов катушек статора).
- Автомобильный двигатель обычно в среднем работает на скорости 2500 об/мин (41 об/с), обороты холостого хода обычно около 1000 об/мин (16 об/с), а максимальные обороты 6000-10 000 об/мин (100-166 об/с).
- Воздушный винт самолета обычно вращается со скоростью между 2000 и 3000 об/мин (30-50 об/с).
- Компьютерный жесткий диск с интерфейсами ATA или SATA обычно вращается со скоростью 5400 или 7200 об/мин (90 или 120 об/с), за редким исключением 10 000 об/мин, а серверные жесткие диски диски с интерфейсами SCSI и SAS обычно используют скорость 10 000 или 15 000 об/мин (160 или 250 об/с).
- Двигатель болида формулы один может развить 18 000 об/мин (300 об/с) (по регламенту сезона 2009)
- Центрифуга по обогащению урана вращается со скоростью 90 000 об/мин (1500 об/с) или быстрее.
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным , оно является равноускоренным .
Как определить мощность и частоту оборотов электродвигателя
Возникла необходимость узнать мощность или частоту оборотов вала и другие параметры электродвигателя, но после внимательного осмотра на его корпусе не нашлось таблички (шылдика) с его наименованием и техническими параметрами. Придется определять самому, для этого есть несколько способов и мы их рассмотрим ниже.
Мощность электродвигателя представляет из себя скорость преобразования электрической энергии, ее принято определять в ваттах.
Чтоб осознать, как это работает, нам понадобится 2 величины: сила тока и напряжение. Сила тока — численность тока, которое проходит через поперечное сечение за некий отрезок времени, ее принято определять в амперах. Напряжение — значение, равная работе по перемещению заряда меж 2-мя точками цепи, ее принято определять в вольтах.
Для расчета мощности используется формула N = A/t, где:
N — мощность;
А — работа;
t — время.
Часто электродвигатель поступает с завода с уже указанными техническими параметрами. Но заявленная мощность не всегда соответствует фактической, а скорее всего она может значить лишь максимальную мощность электропотока.
Так что если на вашем электроинструменте указана, например, мощность в 500 ват, это совсем не значит что инструмент будит потреблять точно 500 ват.
Электродвигатели производят стандартной дискретной мощности, линейки типа 1.5, 2.2, 4 кВт.
Опытный электрик может легко отличить 1.5 от 2.2 кВт всего лишь взглянув на его габариты. Помимо этого он сможет определить количество оборотов двигателя по размеру статора, количеству пар полюсов и диаметра вала.
Еще более опытным в этом деле окажется обмотчик, специалист который занимается перемоткой электродвигателей со 100%-ой уверенностью определит технические параметры вашего электродвигателя.
Если табличка с характеристиками двигателя потеряна для подсчета мощности двигателя нужно измерить силу тока на обмотках ротора и с помощью стандартной формулы найти потребляемую мощность электродвигателя.
Основные способы определения мощности двигателя
Определение мощности по току
. Для этого подключаем двигатель в сеть и контролируем напряжение. Затем поочередно, в цепь каждой из обмоток статора включаем амперметр и замеряем потребляемый ток. После того как мы нашли суму потребляемых токов, полученное число необходимо умножить на фиксированное напряжение в результате получим число определяющее мощность электродвигателя в ваттах.
Определяем мощность по габаритам
. Нужно измерить диаметр сердечника (с внутренней стороны) и его длину.
Дальше если знаем частоту сети нужно узнать синхронную частоту вращения вала.
Умножаем синхронную частоту вращения вала на диаметр сердечника (в сантиметрах) полученную цифру умножаем на 3.14 затем разделяем на частоту сети умноженную на 120. Полученное значение мощности будит в киловаттах.
Замер по счетчику
. Способ считается самым простым. Для этого, для чистоты эксперимента, отключаем все нагрузки в доме. Дальше необходимо включить двигатель на определенное время (например 10 минут) На щетчике будит видно разницу в киловаттах по ней уже легко можно высчитать сколько киловаттах потребляет двигатель. Удобней всего будит воспользоваться портативным электросчетчиком который показывает потребление в киловаттах (ваттах) в режиме реального времени.
Для определения реального показателя мощности, которую выдает двигатель, необходимо найти скорость валового вращения, измеряемую в числе оборотов за секунду, тяговое усилие двигателя.
Частота вращения умножается последовательно на 6,28, показатель силы и радиус вала, который можно вычислить при помощи штангенциркуля. Найденное значение мощности выражается в ваттах.
Определяем рабочее количество оборотов двигателя
.
Самый быстрый способ — посчитать количество катушек (катушечных групп)
Определяем мощность по расчетным таблицам
. С помощью штангенциркуля замеряем диаметр вала, длину мотора (без выступающего вала) и расстояние до оси.Замеряем вылет вала и его выступающую часть, диаметр фланца если он есть, а также расстояние крепежных отверстий. По этим данным с помощью сводной таблицы можно легко определить мощность двигателя и другие характеристики
1,1 КВТ
| Обороты в минуту | 3000 об/мин | 1500 об/мин | 1000 об/мин |
| Габариты h, мм | 71 | 80 | 80 |
| Диаметр вала d1, мм | 19 | 22 | 22 |
| Крепление лап по ширине b10, мм | 112 | 125 | 125 |
| Крепление лап по длине L10, мм | 90 | 100 | 100 |
| Крепление фланца по центрам отверстий d20, мм | 165 | 165 | 165 |
| Замок фланца d25, мм | 130 | 130 | 130 |
1,5 КВТ
| Обороты в минуту | 3000 об/мин | 1500 об/мин | 1000 об/мин |
| Габариты h, мм | 80 | 80 | 90 |
| Диаметр вала d1, мм | 22 | 22 | 24 |
| Крепление лап по ширине b10, мм | 125 | 125 | 140 |
| Крепление лап по длине L10, мм | 100 | 100 | 125 |
| Крепление фланца по центрам отверстий d20, мм | 165 | 165 | 215 |
| Замок фланца d25, мм | 130 | 130 | 180 |
2,2 КВТ
| Обороты в минуту | 3000 об/мин | 1500 об/мин | 1000 об/мин |
| Габариты h, мм | 80 | 90 | 100 |
| Диаметр вала d1, мм | 22 | 24 | 28 |
| Крепление лап по ширине b10, мм | 125 | 140 | 160 |
| Крепление лап по длине L10, мм | 100 | 125 | 140 |
| Крепление фланца по центрам отверстий d20, мм | 165 | 215 | 215 |
| Замок фланца d25, мм | 130 | 180 | 180 |
4 КВТ
| Обороты в минуту | 3000 об/мин | 1500 об/мин | 1000 об/мин |
| Габариты h, мм | 100 | 100 | 112 |
| Диаметр вала d1, мм | 28 | 28 | 32 |
| Крепление лап по ширине b10, мм | 160 | 160 | 190 |
| Крепление лап по длине L10, мм | 112 | 140 | 140 |
| Крепление фланца по центрам отверстий d20, мм | 215 | 215 | 265 |
| Замок фланца d25, мм | 180 | 180 | 230 |
elektt.blogspot.com
Коэффициент оборачиваемости
Основная определяющая скорость оборота оборотных средств формула выглядит так:
Коб — это коэффициент оборачиваемости. Он показывает, сколько оборотов оборотных средств было совершено за конкретный период времени. Другие обозначения в данной формуле: Vp — объем реализации продукции за отчетный период; Oср, — средний остаток оборотных средств за отчетный период. Чаще всего показатель рассчитывается для года, но может быть выбран совершенно любой, нужный для анализа период. Этот коэффициент и есть скорость оборота оборотных средств. Например, годовой оборот мини-магазина мобильных телефонов составил 4 800 000 руб. Средний остаток средств в обороте составлял 357 600 руб. Получаем коэффициент оборачиваемости: 4800000 / 357 600 = 13,4 оборотов.
Как найти число оборотов | О банках и финансах
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то перемещение по окружности нельзя назвать равномерным. оно есть равноускоренным .
Угловая скорость
Выберем на окружности точку 1. Выстроим радиус. За единицу времени точка переместится в пункт 2. Наряду с этим радиус обрисовывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
частота и Период
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
период и Частота взаимосвязаны соотношением
Сообщение с угловой скоростью
Линейная скорость
Любая точка на окружности движется с некоей скоростью. Эту скорость именуют линейной. Направление вектора линейной скорости постоянно совпадает с касательной к окружности.
К примеру, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Разглядим точку на окружности, которая совершает один оборот, время, которое затрачено — это имеется период T. Путь. что преодолевает точка — это имеется протяженность окружности.
Центростремительное ускорение
При перемещении по окружности вектор ускорения неизменно перпендикулярен вектору скорости, направлен в центр окружности.
Применяя прошлые формулы, возможно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (к примеру, это смогут быть точки, каковые лежат на спице колеса), будут иметь однообразные угловые скорости, период и частоту. Другими словами они будут вращаться одинаково, но с различными линейными скоростями. Чем дальше точка от центра, тем стремительнее она будет двигаться.
Закон сложения скоростей честен и для вращательного перемещения. В случае если перемещение тела либо совокупности отсчета не есть равномерным, то закон используется для мгновенных скоростей. К примеру, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости скорости
края движения и вращения карусели человека.
Вращение Почвы
Почва участвует в двух главных вращательных перемещениях: дневном (около собственной оси) и орбитальном (около Солнца). Период вращения Почвы около Солнца образовывает 1 год либо 365 дней. Около собственной оси Почва вращается с запада на восток, период этого вращения образовывает 1 дни либо 24 часа.
Широтой именуется угол между направлением и плоскостью экватора из центра Почвы на точку ее поверхности.
Сообщение со вторым законом Ньютона
В соответствии с второму закону Ньютона обстоятельством любого ускорения есть сила. В случае если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, возможно разной. К примеру, в случае если тело движется по окружности на привязанной к нему веревке, то действующей силой есть сила упругости.
В случае если тело, лежащее на диске, вращается вместе с диском около его оси, то таковой силой есть сила трения. В случае если сила прекратит собственный воздействие, то потом тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Разглядим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение — изменение скорости за единицу времени. Отыщем отличие векторов.
Отличие векторов имеется
. Так как
, возьмём
Перемещение по циклоиде*
В совокупности отсчета, которая связана с колесом, точка равномерно вращается по окружности радиуса R со скоростью
, которая изменяется лишь по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Сейчас перейдем в неподвижную совокупность, связанную с почвой. Полное ускорение точки А останется прошлым и по модулю, и по направлению, поскольку при переходе от одной инерциальной совокупности отсчета к второй ускорение не изменяется. С позиций неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), на протяжении которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Источник: fizmat.by
Как определить обороты электродвигателя
Увлекательные записи:
Подборка статей, которая Вас должна заинтересовать:
- Как найти число оборотов колеса
1.3. Кинематика вращательного перемещения жёсткого тела Как уже отмечалось, вращательным перемещением полностью жёсткого тела около неподвижной оси…
- Полный оборот планет
Разглядим, за какое время происходит полный оборот планет, в то время, когда они возвращаются на ту же точку зодиака, в которой были. Периоды полного…
- Деепричастный оборот. знаки препинания при деепричастном обороте, деепричастии и причастном обороте
July 23, 2015 Что такое деепричастный оборот? Какие конкретно знаки препинания употребляются на письме для выделения деепричастного оборота? Какова роль…
- Почему двигатель не набирает, или плохо набирает обороты, не тянет.
В случае если ваш двигатель не набирает, либо не хорошо усиливается , не тянет, чихает и пукает, согласитесь это весьма не приятно. Тут же давайте…
- Как найти денежный мультипликатор
мировая экономика их роль и Банки в экономике. Банковский и финансовый мультипликаторы Создатель — Матвеева Татьяна Юрьевна, учитель НИУ-ВШЭ…
- Где найти деньги, если их катастрофически не хватает.
Здравствуйте, дорогие читатели. Если вы систематично испытываете проблемы с деньгами и всегда занимаете деньги у друзей, чтобы дотянуть до зарплаты, эта…
kapitalbank.ru
Ускорение, момент и связь их с массой
Помимо приведённых выше величин, с вращением связано ещё несколько моментов. Учитывая же, сколько в автомобиле крутящихся деталей разного веса, их практическое значение нельзя не учесть.
Равномерное вращение – это важная вещь. Вот только нет ни одной детали, которая бы всё время крутилась равномерно. Число оборотов любого крутящегося узла, от коленвала до колеса, всегда в конечном итоге растёт, а затем падает. И та величина, которая показывает, насколько выросли обороты, называется угловым ускорением. Поскольку она производная от угловой скорости, измеряется она в радианах на секунду в квадрате (как линейное ускорение – в метрах на секунду в квадрате).
С движением и её изменением во времени связан и другой аспект – момент импульса. Если до этого момента мы могли рассматривать только чисто математические особенности движения, то здесь уже нужно учитывать то, что каждая деталь имеет массу, которая распределена вокруг оси. Он определяется соотношением начального положения точки с учётом направления движения – и импульса, то есть произведения массы на скорость. Зная момент импульса, возникающий при вращении, можно определить, какая нагрузка будет приходиться на каждую деталь при её взаимодействии с другой
Формула угловой скорости в физике
Определение и формула угловой скорости
Определение
Круговым движением точки
вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси
называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота . Часто используют вектор элементарного поворота , который равен по величине элементарному углу поворота тела замаленький отрезок времени dtи направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.
Определение
Угловой скоростью
называют скорость изменения угла поворота и обозначают ее обычно буквой . Математически определение угловой скорости записывают так:
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ( при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
где – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ). Угловая скорость связана с периодом обращения как:
С числом оборотов в единицу времени () угловая скорость связана формулой:
Понятия периода обращения и числа оборотов в единицу времени иногда используют и для описания неравномерного вращения, но понимают при этом под мгновенным значением T, время за которое тело делало бы один оборот, если бы оно вращалось равномерно с данной мгновенной величиной скорости.
Формула, связывающая линейную и угловую скорости
Линейная скорость точки А (рис.1), которая расположена на расстоянии R от оси вращения связана с вектором угловой скорости следующим векторным произведением:
где – перпендикулярная к оси вращения компонента радиус-вектора точки (рис.1). Вектор проводят от точки, находящейся на оси вращения к рассматриваемой точке.
Единицы измерения угловой скорости
Основной единицей измерения угловой скорости в системе СИ является: []=рад/с
В СГС: []=рад/с
Видео
Директор компании, у которого перед глазами есть только показатели прибыли и общей рентабельности не всегда может понять, как их корректировать в нужную сторону. Для того чтобы иметь в руках все рычаги управления, совершенно необходимо провести также расчет оборачиваемости оборотных средств. Картина использования оборотных средств складывается из четырех основных показателей:
- Длительность оборота (определяется в днях);
- Сколько раз оборотные средства делают оборот в отчетном периоде;
- Сколько оборотных средств приходится на единицу реализованной продукции;
- Коэффициент загрузки средств в обороте.
Рассмотрим расчет этих данных на примере обычного предприятия, а также расчет ряда важных коэффициентов для понимания значения показателей оборачиваемости в общей картине успешности компании.
Примечания
Wikimedia Foundation . 2010 .
Смотреть что такое «Оборот в минуту» в других словарях:
- оборот в минуту
— Единица измерения, применяемая для характеристики параметров центрифугирования по скорости вращения ротора (наряду с показателем g ускорение силы тяжести). [Арефьев В.А., Лисовенко Л.А. Англо русский толковый словарь генетических терминов 1995… … Справочник технического переводчика
Rpm (round per minute) оборот в минуту. Eдиница измерения, применяемая для характеристики параметров центрифугирования по скорости вращения ротора (наряду с показателем g ускорение силы тяжести). (Источник: «Англо русский толковый словарь… … Молекулярная биология и генетика. Толковый словарь.
Внесистемная ед. частоты вращения. Обозначение об/мин. 1 об/мин = 1 мин 116,667 с 1 … Большой энциклопедический политехнический словарь
Оборота, м. 1. Полный круг вращения, круговой поворот. Оборот колеса. Вал делает 20 оборотов в минуту. || Движение туда и обратно, возврат на исходное место. Ускорить оборот вагонов. 2. Отдельная стадия, законченный процесс в последовательной… … Толковый словарь Ушакова
— (Revolution) на судах флота в отношении работы главной машины полный оборот (на 860°) гребного вала, вращаемого этой машиной. Иметь столько то оборотов приказание в машину, требующее, чтобы гребной вал давал в минуту указанное количество оборотов … Морской словарь
У этого термина существуют и другие значения, см. Оборот. Оборот (цикл, круг) единица измерения угла, либо фазы колебаний. При измерении угла обычно используется название «оборот», а при измерении фазы «цикл». Один оборот равен… … Википедия
Сущ., м., употр. сравн. часто Морфология: (нет) чего? оборота, чему? обороту, (вижу) что? оборот, чем? оборотом, о чём? об обороте; мн. что? обороты, (нет) чего? оборотов, чему? оборотам, (вижу) что? обороты, чем? оборотами, о чём? об оборотах 1 … Толковый словарь Дмитриева
оборот
— а; м. см. тж. оборотный, оборачиваемость 1) а) Полный круг вращения; круговой поворот. Оборо/т колеса. Количество оборотов в минуту. Повернуть ключ на два оборота … Словарь многих выражений
А; м. 1. Полный круг вращения; круговой поворот. О. колеса. Количество оборотов в минуту. Повернуть ключ на два оборота. // Спец. Перевёртывание с одной стороны на другую, обратную. Вспашка с оборотом пласта. // мн.: обороты, ов. Спец. разг. О… … Энциклопедический словарь
количество круговых делений в минуту
— 3.1 количество круговых делений в минуту (dial division per minute): Скорость вращения мешалки, используемой в этом методе. Примечание Один полный оборот мешалки (360°) разделен на 100 делений. Показатель текучести характеризуется скоростью… … Словарь-справочник терминов нормативно-технической документации
- Основные законы Динамики. Законы Ньютона — первый, второй, третий. Принцип относительности Галилея. Закон всемирного тяготения. Сила тяжести. Силы упругости. Вес. Силы трения — покоя, скольжения, качения + трение в жидкостях и газах.
- Кинематика. Основные понятия. Равномерное прямолинейное движение. Равноускоренное движение. Равномерное движение по окружности. Система отсчёта. Траектория, перемещение, путь, уравнение движения, скорость, ускорение, связь линейной и угловой скорости.
- Простые механизмы. Рычаг (рычаг первого рода и рычаг второго рода). Блок (неподвижный блок и подвижный блок). Наклонная плоскость. Гидравлический пресс. Золотое правило механики
- Законы сохранения в механике. Механическая работа, мощность, энергия, закон сохранения импульса, закон сохранения энергии, равновесие твердых тел
- Вы сейчас здесь:
Движение по окружности. Уравнение движения по окружности. Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости - Механические колебания. Свободные и вынужденные колебания. Гармонические колебания. Упругие колебания. Математический маятник. Превращения энергии при гармонических колебаниях
- Механические волны. Скорость и длина волны. Уравнение бегущей волны. Волновые явления (дифракция. интерференция…)
- Гидромеханика и аэромеханика. Давление, гидростатическое давление. Закон Паскаля. Основное уравнение гидростатики. Сообщающиеся сосуды. Закон Архимеда. Условия плавания тел. Течение жидкости. Закон Бернулли. Формула Торричели
- Молекулярная физика. Основные положения МКТ. Основные понятия и формулы. Свойства идеального газа. Основное уравнение МКТ. Температура. Уравнение состояния идеального газа. Уравнение Менделеева-Клайперона. Газовые законы — изотерма, изобара, изохора
- Волновая оптика. Корпускулярно-волновая теория света. Волновые свойства света. Дисперсия света. Интерференция света. Принцип Гюйгенса-Френеля. Дифракция света. Поляризация света
- Термодинамика. Внутренняя энергия. Работа. Количество теплоты. Тепловые явления. Первый закон термодинамики. Применение первого закона термодинамики к различным процессам. Уравнение теплового балланса. Второй закон термодинамики. Тепловые двигатели
- Электростатика. Основные понятия. Электрический заряд. Закон сохранения электрического заряда. Закон Кулона. Принцип суперпозиции. Теория близкодействия. Потенциал электрического поля. Конденсатор.
- Постоянный электрический ток. Закон Ома для участка цепи. Работа и мощность постоянного тока. Закон Джоуля-Ленца. Закон Ома для полной цепи. Закон электролиза Фарадея. Электрические цепи — последовательное и параллельное соединение. Правила Кирхгофа.
- Электромагнитные колебания. Свободные и вынужденные электромагнитные колебания. Колебательный контур. Переменный электрический ток. Конденсатор в цепи переменного тока. Катушка индуктивности («соленоид») в цепи переменного тока.
- Элементы теории относительности. Постулаты теории относительности. Относительность одновременности, расстояний, промежутков времени. Релятивистский закон сложения скоростей. Зависимость массы от скорости. Основной закон релятивистский динамики…
- Погрешности прямых и косвенных измерений. Абсолютная, относительная погрешность. Систематические и случайные погрешности. Среднее квадратическое отклонение (ошибка). Таблица определения погрешностей косвенных измерений различных функций.
- N – количество оборотов вокруг оси или по окружности,
- t – время, за которое они были совершены.
Количество повторений каких-либо событий или их возникновения за одну единицу таймера называется частотой. Это физическая величина измеряется в герцах – Гц (Hz). Она обозначается буквами ν, f, F, и есть отношение количества повторяющихся событий к промежутку времени, в течение которого они произошли.
При обращении предмета вокруг своего центра можно говорить о такой физической величине, как частота вращения, формула:
В системе СИ обозначается как – с-1 (s-1) и именуется как обороты в секунду (об/с). Применяют и другие единицы вращения. При описании вращения планет вокруг Солнца говорят об оборотах в часах. Юпитер делает одно вращение в 9,92 часа, тогда как Земля и Луна оборачиваются за 24 часа.