For other uses, see Revolutions per minute (values).
"rpm" redirects here. For other uses, see RPM (values).
| This article need additional quotes for verification . |
| RPM | |
| Unit | Rotational speed |
| Symbol | rpm or rpm |
| Conversions | |
| 1 rpm in... | … equals … |
| Angular velocity SI | 2π/60 rad/s ≈ 0.1047198 rad/s |
| SI frequency | 1/60 Hz ≈ 0.01666667 Hz |
| Derived speed SI | 1/60 s−1, 1/60/ s |
| Derived rotation speed SI | 1 min−1, 1 min |
RPM
(abbreviated
rpm
,
rpm
,
rpm
,
rpm
, or with the designation min−1) - the number of turns in one minute. It is a unit of rotation speed or frequency of rotation around a fixed axis.
Rotational motion (circular movement of a body) | Formulas and calculations online
The laws that determine the motion of a body in a circle are similar to the laws of translational motion. The equations describing rotational motion can be derived from the equations of translational motion by making the following substitutions in the latter:
If: move s
- angular displacement (angle of rotation)
φ
, speed
u
- angular velocity
ω
, acceleration
a
- angular acceleration
α
Rotational movement, characteristics
| Rotational movement | Angular velocity | Angular acceleration |
| Uniform | Constant | Equal to zero |
| Uniformly accelerated | Changes evenly | Constantly |
| Unevenly accelerated | Changes unevenly | Variable |
Angle of rotation
In all equations of rotational motion, angles are specified in radians, abbreviated as (rad)
.
If φ
is the angular displacement in radians,
s
is the length of the arc enclosed between the sides of the angle of rotation,
r
is the radius, then by definition of radian
\[ φ = \frac{s}{r} \]
Relationship between angle units
\[ \frac[-1.35]{φ_{rad}}{φ_{°}} = \frac[-1.2]{π}{180°} \]
| $ 1 rad = 57.3° $ | $ 1° = 17.45 mrad $ | $ 1´ = 291 microrad $ |
Note:
The name of the unit radian (rad) is usually indicated in formulas only in cases where it can be confused with a degree. Since a radian is equal to the ratio of the lengths of two segments (1rad = 1m/1m = 1), it has no dimension.
The relationship between angular velocity, angular displacement and time for all types of circular motion is clearly visible on the angular velocity graph (dependence ω
from
t
). Therefore, the graph can determine what angular velocity a body has at a given moment in time and at what angle it has turned since the beginning of its movement (it is characterized by the area under the curve).
In addition, to represent the relationships between these quantities, use a graph of angular displacement (dependence φ
on
t
) and a graph of angular acceleration (dependence
α
on
t
).
Speed
A characteristic of all types of rotation is the number of revolutions n
or an equivalent characteristic - frequency
f
. Both quantities characterize the number of revolutions per unit time.
SI unit of frequency (or number of revolutions)
\[ [n] = [f] = \frac{Revolutions}{Second} = \frac{(rev)}{s} = \frac{1}{c} = Hertz \]
In engineering, the number of revolutions is usually measured in revolutions per minute (rpm) = 1/min.
Thus, the reciprocal of the number of revolutions is the duration of one revolution.
If n
- number of revolutions,
f
- frequency,
T
- duration of one revolution, period,
φ
- angular displacement,
N
- total number of revolutions,
t
- time, duration of rotation,
ω
- angular frequency, then
Period
\[ T = \frac{1}{f} = \frac{1}{n} \]
Angular movement
The angular displacement is equal to the product of the total number of revolutions and 2π:
\[ φ = 2 π N \]
Angular velocity
From the formula for one revolution it follows:
\[ ω = 2 π f = \frac{2π}{T} \]
Please note:
•
formulas (1)—(6) are valid for all types of rotational motion - both for uniform motion and for accelerated motion.
These can include constant values, average values, start and end values, and any instantaneous values. •
contrary to its name, the number of revolutions
n
is not a number, but a physical quantity.
•
a distinction must be made between the number of revolutions
n
and the total number of revolutions
N
.
To help the student
Rotational movement (body movement in a circle) | page 421 |
www.fxyz.ru
Rotation angle and period of revolution
Consider point A on an object rotating around its axis. When circulating over a certain period of time, it will change its position on the circle line by a certain angle. This is the rotation angle. It is measured in radians, because the unit is a segment of a circle equal to the radius. Another value for measuring the angle of rotation is a degree.
When, as a result of the rotation, point A returns to its original place, it means that it has completed a full rotation. If its movement is repeated n times, then we speak of a certain number of revolutions. Based on this, you can consider 1/2, 1/4 turn and so on. A striking practical example of this is the path that a cutter takes when milling a part fixed in the center of the machine spindle.
Formula for calculating rotation speed
When designing equipment, it is necessary to know the speed of the electric motor. To calculate the rotation speed, there are special formulas that are different for AC and DC motors.
Tachometer
Synchronous and asynchronous electric machines
There are three types of AC motors: synchronous, the angular speed of the rotor coincides with the angular frequency of the stator magnetic field; asynchronous - in them the rotation of the rotor lags behind the rotation of the field; commutator motors, the design and operating principle of which are similar to DC motors.
Synchronous speed
The rotation speed of an AC electric machine depends on the angular frequency of the stator magnetic field. This speed is called synchronous. In synchronous motors, the shaft rotates at the same speed, which is an advantage of these electric machines.
To do this, the rotor of high-power machines has a winding to which a constant voltage is applied, creating a magnetic field. In low power devices, permanent magnets are inserted into the rotor, or there are pronounced poles.
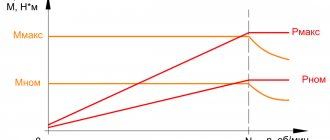
Slip
In asynchronous machines, the number of shaft revolutions is less than the synchronous angular frequency. This difference is called the "S" slip. Due to sliding, an electric current is induced in the rotor and the shaft rotates. The larger S, the higher the torque and the lower the speed. However, if the slip exceeds a certain value, the electric motor stops, begins to overheat and may fail. The rotation speed of such devices is calculated using the formula in the figure below, where:
- n – number of revolutions per minute,
- f – network frequency,
- p – number of pole pairs,
- s – slip.
Formula for calculating the speed of an asynchronous motor
There are two types of such devices:
- With squirrel-cage rotor. The winding in it is cast from aluminum during the manufacturing process;
- With wound rotor. The windings are made of wire and are connected to additional resistances.
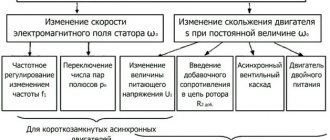
Speed adjustment
During operation, it becomes necessary to adjust the speed of electrical machines. This is done in three ways:
- Increasing additional resistance in the rotor circuit of electric motors with a wound rotor. If it is necessary to greatly reduce the speed, it is possible to connect not three, but two resistances;
- Connecting additional resistances in the stator circuit. It is used to start high-power electrical machines and to regulate the speed of small electric motors. For example, the speed of a table fan can be reduced by connecting an incandescent lamp or capacitor in series with it. The same result is achieved by reducing the supply voltage;
- Changing the network frequency. Suitable for synchronous and asynchronous motors.
Attention! The rotation speed of commutator electric motors operating from an alternating current network does not depend on the frequency of the network.
DC motors
In addition to AC machines, there are electric motors connected to a DC network. The speed of such devices is calculated using completely different formulas.
Rated rotation speed
The speed of a DC machine is calculated using the formula in the figure below, where:
- n – number of revolutions per minute,
- U – network voltage,
- Rya and Iya – armature resistance and current,
- Ce – motor constant (depending on the type of electric machine),
- Ф – stator magnetic field.
These data correspond to the nominal values of the parameters of the electric machine, the voltage on the field winding and the armature or the torque on the motor shaft. Changing them allows you to adjust the rotation speed. It is very difficult to determine the magnetic flux in a real motor, so calculations are made using the current flowing through the field winding or armature voltage.
Formula for calculating the speed of a DC motor
The speed of commutator AC motors can be found using the same formula.
Speed adjustment
Adjustment of the speed of an electric motor operating from a DC network is possible within a wide range. It is possible in two ranges:
- Up from nominal. To do this, the magnetic flux is reduced using additional resistances or a voltage regulator;
- Down from par. To do this, it is necessary to reduce the voltage on the armature of the electric motor or connect a resistance in series with it. In addition to reducing the speed, this is done when starting the electric motor.
Knowing what formulas are used to calculate the rotation speed of an electric motor is necessary when designing and setting up equipment.
Video
Rate the article:
elquanta.ru
Examples
- On gramophone records, the rotation speed is specified in rpm: for example, standard rotation speeds are 16 + 2 ⁄ 3, 33 + 1 ⁄ 3, 45 or 78 rpm (5 ⁄ 18, 5 ⁄ 9, 3 ⁄ 4, or 1, 3 rps respectively).
- The new ultrasonic drilling machines have rotation speeds of up to 800,000 rpm (13,300 rps).
- The second hand of a watch rotates at a frequency of 1 rpm.
- Audio CD players read at 150 kB/s and therefore at a disk rotation speed of approximately 500 rpm (8 rps) at the inner edge and 200 rpm (3.5 rps) at the outer edge border. CD drives have rotation speeds that are multiples of these numbers, even when using variable read speed.
- DVD players also typically read discs at a constant linear speed. The rotation speed varies from 1,530 rpm (25.5 rps), when reading at the inner edge, and 630 rpm (10.5 rps) on the outer edge of the disk. DVD drives also operate at speeds that are multiples of the above figures.
- The washing machine drum can rotate at speeds from 500 to 2000 rpm (8-33 rps) during the spin cycle.
- The generator turbine rotates at 3000 rpm (50 rps) or 3600 rpm (60 rps), depending on the country (see Alternating Current#Frequency Standards). The generator shaft of a hydroelectric power station can rotate slower: up to 2 rps (in this case, the network frequency of 50 Hz is obtained due to the presence of a larger number of poles of the stator coils).
- A car engine typically runs at an average speed of 2500 rpm (41 rpm), idle speed is usually around 1000 rpm (16 rpm), and maximum speed is 6000-10,000 rpm (100-166 rpm). /With).
- An airplane propeller typically rotates at speeds between 2000 and 3000 rpm (30-50 rps).
- A computer hard drive with ATA or SATA interfaces usually spins at 5400 or 7200 rpm (90 or 120 rpm), with rare exceptions of 10,000 rpm, and server hard drives with SCSI and SAS interfaces usually use a speed of 10 000 or 15,000 rpm (160 or 250 rpm).
- The engine of a formula one car can develop 18,000 rpm (300 rps) (according to the regulations of the 2009 season)
- A uranium enrichment centrifuge spins at 90,000 rpm (1,500 rps) or faster.
Since linear speed uniformly changes direction, the circular motion cannot be called uniform, it is uniformly accelerated.
How to determine the power and speed of an electric motor
There was a need to find out the power or shaft speed and other parameters of the electric motor, but after a careful inspection, there was no plate (nameplate) with its name and technical parameters on its body. You'll have to determine it yourself; there are several ways to do this, and we'll look at them below.
The power of an electric motor is the rate at which electrical energy is converted and is usually determined in watts.
To understand how this works, we need 2 quantities: current and voltage. Current strength is the amount of current that passes through a cross section over a certain period of time; it is usually determined in amperes. Voltage is a value equal to the work done to move a charge between two points in a circuit; it is usually determined in volts.
To calculate power, use the formula N = A/t, where:
N—power;
What about work;
t — time.
Often the electric motor comes from the factory with technical parameters already specified. But the declared power does not always correspond to the actual one, and most likely it can only mean the maximum power of the electric flow.
So if your power tool indicates, for example, a power of 500 watts, this does not mean at all that the tool will consume exactly 500 watts.
Electric motors produce standard discrete power, such as 1.5, 2.2, 4 kW.
An experienced electrician can easily distinguish 1.5 from 2.2 kW just by looking at its dimensions. In addition, he will be able to determine the number of engine revolutions based on the stator size, number of pole pairs and shaft diameter.
A wrapper will be even more experienced in this matter; a specialist who rewinds electric motors will determine the technical parameters of your electric motor with 100% confidence.
If the motor rating plate is lost, to calculate the motor power, you need to measure the current on the rotor windings and use the standard formula to find the power consumption of the electric motor.
Basic methods for determining engine power
Determination of power by current
. To do this, we connect the motor to the network and control the voltage. Then, one by one, we connect an ammeter to the circuit of each of the stator windings and measure the current consumed. After we have found the sum of consumed currents, the resulting number must be multiplied by a fixed voltage, as a result we get a number that determines the power of the electric motor in watts.
Determining power by size
. You need to measure the diameter of the core (from the inside) and its length.
Next, if we know the network frequency, we need to find out the synchronous shaft rotation speed.
We multiply the synchronous speed of the shaft by the diameter of the core (in centimeters), multiply the resulting figure by 3.14, then divide it by the network frequency multiplied by 120. The resulting power value is in kilowatts.
Measuring by meter
.
The method is considered the simplest. To do this, for the purity of the experiment, we turn off all the loads in the house. Next, you need to turn on the engine for a certain time (for example, 10 minutes). On the brush, you can see the difference in kilowatts; from this you can easily calculate how many kilowatts the engine consumes. The most convenient way is to use a portable electric meter that shows consumption in kilowatts (watts) in real time. To determine the real indicator of the power that the engine produces, it is necessary to find the shaft rotation speed, measured in the number of revolutions per second, and the engine tractive effort.
The rotational speed is multiplied sequentially by 6.28, an indicator of force and the radius of the shaft, which can be calculated using a caliper. The found power value is expressed in watts.
Determining the operating speed of the engine
.
The fastest way is to count the number of coils (coil groups)
We determine power using calculation tables
. Using a caliper, we measure the diameter of the shaft, the length of the motor (without the protruding shaft) and the distance to the axle. We measure the extension of the shaft and its protruding part, the diameter of the flange if there is one, as well as the distance of the mounting holes. Using this data, using a pivot table, you can easily determine engine power and other characteristics
1.1 kW
| Revolutions per minute | 3000 rpm | 1500 rpm | 1000 rpm |
| Dimensions h, mm | 71 | 80 | 80 |
| Shaft diameter d1, mm | 19 | 22 | 22 |
| Mounting paws width b10, mm | 112 | 125 | 125 |
| Fastening of paws along length L10, mm | 90 | 100 | 100 |
| Flange fastening at the centers of holes d20, mm | 165 | 165 | 165 |
| Flange lock d25, mm | 130 | 130 | 130 |
1.5 kW
| Revolutions per minute | 3000 rpm | 1500 rpm | 1000 rpm |
| Dimensions h, mm | 80 | 80 | 90 |
| Shaft diameter d1, mm | 22 | 22 | 24 |
| Mounting paws width b10, mm | 125 | 125 | 140 |
| Fastening of paws along length L10, mm | 100 | 100 | 125 |
| Flange fastening at the centers of holes d20, mm | 165 | 165 | 215 |
| Flange lock d25, mm | 130 | 130 | 180 |
2.2 kW
| Revolutions per minute | 3000 rpm | 1500 rpm | 1000 rpm |
| Dimensions h, mm | 80 | 90 | 100 |
| Shaft diameter d1, mm | 22 | 24 | 28 |
| Mounting paws width b10, mm | 125 | 140 | 160 |
| Fastening of paws along length L10, mm | 100 | 125 | 140 |
| Flange fastening at the centers of holes d20, mm | 165 | 215 | 215 |
| Flange lock d25, mm | 130 | 180 | 180 |
4 KW
| Revolutions per minute | 3000 rpm | 1500 rpm | 1000 rpm |
| Dimensions h, mm | 100 | 100 | 112 |
| Shaft diameter d1, mm | 28 | 28 | 32 |
| Mounting paws width b10, mm | 160 | 160 | 190 |
| Fastening of paws along length L10, mm | 112 | 140 | 140 |
| Flange fastening at the centers of holes d20, mm | 215 | 215 | 265 |
| Flange lock d25, mm | 180 | 180 | 230 |
elektt.blogspot.com
Turnover ratio
The main formula determining the rate of turnover of working capital is as follows:
Cob is the turnover ratio. It shows how many turnovers of working capital were made during a specific period of time. Other designations in this formula: Vp - volume of product sales for the reporting period; Osr is the average balance of working capital for the reporting period. Most often, the indicator is calculated for the year, but absolutely any period needed for analysis can be selected. This coefficient is the rate of turnover of working capital. For example, the annual turnover of a mini-store of mobile phones was 4,800,000 rubles. The average balance in circulation was RUB 357,600. We get the turnover ratio: 4,800,000 / 357,600 = 13.4 revolutions.
How to find the number of revolutions | About banks and finance
Testing online
Since the linear speed uniformly changes direction, the movement around the circle cannot be called uniform. it is uniformly accelerated.
Angular velocity
Let's select point 1 on the circle. Let's build a radius. In a unit of time, the point will move to point 2. Along with this, the radius outlines the angle. Angular velocity is numerically equal to the angle of rotation of the radius per unit time.
frequency and period
The rotation period T is the time during which the body makes one revolution.
Rotation frequency is the number of revolutions per second.
Period and Frequency are interconnected by the ratio
Message with angular velocity
Linear speed
Any point on a circle moves at a certain speed. This speed is called linear. The direction of the linear velocity vector always coincides with the tangent to the circle.
For example, sparks from under a grinding machine move, repeating the direction of instantaneous speed.
Let's look at a point on the circle that makes one revolution, the time it takes is the period T. Path. What a point overcomes is the extent of the circle.
Centripetal acceleration
When moving around a circle, the acceleration vector is invariably perpendicular to the velocity vector, directed towards the center of the circle.
Using the previous formulas, it is possible to derive the following relations
Points lying on the same straight line emanating from the center of the circle (for example, these could be points that lie on the spokes of a wheel) will have uniform angular velocities, period and frequency. In other words, they will rotate the same way, but with different linear speeds. The further the point is from the center, the faster it will move.
The law of addition of velocities is also valid for rotational movement. If the movement of a body or a reference set is not uniform, then the law is used for instantaneous velocities. For example, the speed of a person walking along the edge of a rotating carousel is equal to the vector sum of the linear speed of the speed
edges of human carousel movement and rotation.
Soil Rotation
The soil participates in two main rotational movements: diurnal (near its own axis) and orbital (near the Sun). The period of rotation of the Earth around the Sun is 1 year or 365 days. The soil rotates around its own axis from west to east, the period of this rotation is 1 day or 24 hours.
Latitude is the angle between the direction and the plane of the equator from the center of the Soil to a point on its surface.
Message with Newton's second law
According to Newton's second law, the force behind any acceleration is force. If a moving body experiences centripetal acceleration, then the nature of the forces that cause this acceleration may be different. For example, if a body moves in a circle on a rope tied to it, then the acting force is the elastic force.
If a body lying on a disk rotates together with the disk about its axis, then such a force is the friction force. If the force stops its own influence, then the body will move in a straight line
How to derive the formula for centripetal acceleration
Let us consider the movement of a point on a circle from A to B. The linear speed is equal to vA and vB, respectively. Acceleration is the change in speed per unit time. Let's find the difference between the vectors.
There is a difference between the vectors
. Because
, let's take
Moving along a cycloid*
In the reference set, which is associated with the wheel, the point rotates uniformly along a circle of radius R with a speed
, which changes only in direction. The centripetal acceleration of a point is directed radially towards the center of the circle.
Now let's move on to the stationary aggregate associated with the soil. The total acceleration of point A will remain the past both in magnitude and in direction, since during the transition from one inertial frame of reference to the second, the acceleration does not change. From the position of a stationary observer, the trajectory of point A is no longer a circle, but a more complex curve (cycloid), along which the point moves unevenly.
Instantaneous speed is determined by the formula
Source: fizmat.by
How to determine electric motor speed
Fascinating posts:
A selection of articles that should interest you:
- How to find the number of wheel revolutions
1.3. Kinematics of rotational movement of a rigid body As already noted, rotational movement of a completely rigid body around a fixed axis...
- Complete revolution of planets
Let's look at how long it takes for the planets to complete a revolution, at the time when they return to the same point in the zodiac at which they were. Periods of full...
- Participial turnover. punctuation marks for participial phrases, participles and participial phrases
July 23, 2015 What is an adverbial phrase? What specific punctuation marks are used in writing to highlight adverbial phrases? What is the role...
- Why doesn’t the engine pick up speed, or picks up speed poorly, or doesn’t pull.
If your engine does not rev up, or does not power up well, does not pull, sneezes and farts, you must agree that this is very unpleasant. Let's go right now...
- How to Find a Money Multiplier
world economy, their role and Banks in the economy. Banking and financial multipliers Creator - Tatyana Yuryevna Matveeva, teacher at the National Research University Higher School of Economics...
- Where to find money if there is a catastrophic shortage of it.
Hello dear readers. If you regularly have problems with money and always borrow money from friends in order to reach your salary, this...
kapitalbank.ru
Acceleration, moment and their connection with mass
In addition to the above values, there are several other issues associated with rotation. Considering how many rotating parts of different weights there are in a car, their practical importance cannot be ignored.
Even rotation is important. But there is not a single part that rotates evenly all the time. The number of revolutions of any rotating component, from the crankshaft to the wheel, always eventually rises and then falls. And the value that shows how much the revolutions have increased is called angular acceleration. Since it is a derivative of angular velocity, it is measured in radians per second squared (like linear acceleration - in meters per second squared).
Another aspect is associated with movement and its change in time - angular momentum. If up to this point we could only consider purely mathematical features of movement, then here we need to take into account the fact that each part has a mass that is distributed around its axis. It is determined by the ratio of the initial position of the point, taking into account the direction of movement - and momentum, that is, the product of mass and speed. Knowing the moment of impulse arising during rotation, it is possible to determine what load will fall on each part when it interacts with another
Formula for angular velocity in physics
Definition and formula of angular velocity
Determination
of a point by circular motion
around a certain axis is a movement in which the trajectory of a point is a circle with a center that lies on the axis of rotation, while the plane of the circle is perpendicular to this axis.
Rotation of the body around an axis
called a movement in which all points of the body make circular movements around this axis.
Movement during rotation is characterized using the angle of rotation. The elementary rotation vector is often used, which is equal in magnitude to the elementary angle of rotation of the body over a small period of time dt and is directed along the instantaneous axis of rotation in the direction from where this rotation is seen to be realized counterclockwise. It should be noted that only elementary angular displacements are vectors. Angles of rotation to finite values are not vectors.
Definition
Angular velocity
is called the rate of change in the angle of rotation and is usually denoted by the letter . Mathematically, the definition of angular velocity is written as follows:
Angular velocity is a vector quantity (it is an axial vector). It has a direction along the instantaneous axis of rotation coinciding with the direction of the translational right screw, if it is rotated in the direction of rotation of the body (Fig. 1).
The angular velocity vector can undergo changes both due to changes in the speed of rotation of the body around the axis (change in the module of angular velocity) and due to the rotation of the axis of rotation in space (while changing the direction).
Uniform rotation
If a body rotates through the same angle at equal intervals of time, then such rotation is called uniform. In this case, the angular velocity module is found as:
where is the angle of rotation, t is the time during which this rotation is completed.
Uniform rotation is often characterized by its revolution period (T), which is the time it takes for a body to complete one revolution). Angular velocity is related to the period of revolution as:
The angular velocity is related to the number of revolutions per unit time () by the formula:
The concepts of the period of revolution and the number of revolutions per unit time are sometimes used to describe uneven rotation, but are understood as the instantaneous value T, the time during which the body would make one revolution if it rotated uniformly at a given instantaneous speed.
Formula relating linear and angular velocities
The linear velocity of point A (Fig. 1), which is located at a distance R from the axis of rotation, is related to the angular velocity vector by the following vector product:
where is the component of the radius vector of the point perpendicular to the axis of rotation (Fig. 1). The vector is drawn from a point located on the axis of rotation to the point in question.
Units of angular velocity
The basic unit of measurement of angular velocity in the SI system is: []=rad/s
In GHS: []=rad/s
Video
The director of a company, who only has indicators of profit and overall profitability before his eyes, cannot always understand how to adjust them in the right direction. In order to have all the control levers in your hands, it is absolutely necessary to calculate the turnover of working capital. The picture of the use of working capital consists of four main indicators:
- Duration of turnover (determined in days);
- How many times do working capital turn over in the reporting period;
- How much working capital is there per unit of products sold;
- Load factor of funds in circulation.
Let's consider the calculation of this data using the example of an ordinary enterprise, as well as the calculation of a number of important coefficients for understanding the significance of turnover indicators in the overall picture of the company's success.
Notes
Wikimedia Foundation. 2010.
See what “Revolutions per minute” is in other dictionaries:
- revolutions per minute
— A unit of measurement used to characterize centrifugation parameters by rotor rotation speed (along with the indicator g, gravity acceleration). [Arefyev V.A., Lisovenko L.A. English-Russian explanatory dictionary of genetic terms 1995... ... Technical Translator's Guide
Rpm (round per minute) revolutions per minute. A unit of measurement used to characterize centrifugation parameters by rotor rotation speed (along with the g indicator, gravity acceleration). (Source: “English-Russian explanatory dictionary... ... Molecular biology and genetics. Explanatory dictionary.
Non-system units rotation speed. Designation rpm 1 rpm = 1 min 116.667 s 1 ... Big Encyclopedic Polytechnic Dictionary
Turns, m. 1. Full circle of rotation, circular turn. Wheel revolution. The shaft makes 20 revolutions per minute. || Moving back and forth, returning to the starting place. Speed up the turnover of wagons. 2. A separate stage, a completed process in a sequential... ... Ushakov’s Explanatory Dictionary
- (Revolution) on fleet vessels, in relation to the operation of the main machine, a full rotation (860°) of the propeller shaft rotated by this machine. To have so many revolutions is an order in a machine, requiring that the propeller shaft give a specified number of revolutions per minute ... Marine Dictionary
This term has other meanings, see Verso. Revolution (cycle, circle) is a unit of measurement of angle or phase of oscillation. When measuring angle, the name "revolution" is usually used, and when measuring phase, "cycle". One revolution is equal to... ... Wikipedia
Noun, m., used. compare often Morphology: (no) what? turnover, what? turn around, (I see) what? turnover, what? in turn, about what? about turnover; pl. What? revolutions, (no) what? revolutions, what? revolutions, (I see) what? rpm, what? revs, about what? about revolutions 1 ... Dmitriev's Explanatory Dictionary
turnover
- A; m. see also. negotiable, turnover 1) a) Full circle of rotation; circular turn. Revolution/t of wheel. Number of revolutions per minute. Turn the key two turns... Dictionary of many expressions
A; m. 1. Full circle of rotation; circular turn. O. wheels. Number of revolutions per minute. Turn the key two turns. // Special Turning from one side to the other, reverse. Plowing with formation turnover. // plural: revolutions, ov. Specialist. decomposition Oh... ... Encyclopedic Dictionary
number of circular divisions per minute
— 3.1 dial division per minute: The speed of rotation of the stirrer used in this method. Note One complete revolution of the stirrer (360°) is divided into 100 divisions. The turnover rate is characterized by speed... ... Dictionary of terms of normative and technical documentation
- Basic laws of Dynamics. Newton's laws - first, second, third. Galileo's principle of relativity. The law of universal gravitation. Gravity. Elastic forces. Weight. Friction forces - rest, sliding, rolling + friction in liquids and gases.
- Kinematics. Basic concepts. Uniform straight motion. Uniformly accelerated motion. Uniform movement in a circle. Reference system. Trajectory, displacement, path, equation of motion, speed, acceleration, relationship between linear and angular speed.
- Simple mechanisms. Lever (lever of the first kind and lever of the second kind). Block (fixed block and movable block). Inclined plane. Hydraulic Press. The golden rule of mechanics
- Conservation laws in mechanics. Mechanical work, power, energy, law of conservation of momentum, law of conservation of energy, equilibrium of solids
- You are here now:
Circular movement. Equation of motion in a circle. Angular velocity. Normal = centripetal acceleration. Period, frequency of circulation (rotation). Relationship between linear and angular velocity - Mechanical vibrations. Free and forced vibrations. Harmonic vibrations. Elastic vibrations. Mathematical pendulum. Energy transformations during harmonic oscillations
- Mechanical waves. Speed and wavelength. Traveling wave equation. Wave phenomena (diffraction, interference...)
- Fluid mechanics and aeromechanics. Pressure, hydrostatic pressure. Pascal's law. Basic equation of hydrostatics. Communicating vessels. Archimedes' law. Sailing conditions tel. Fluid flow. Bernoulli's law. Torricelli formula
- Molecular physics. Basic provisions of the ICT. Basic concepts and formulas. Properties of an ideal gas. Basic MKT equation. Temperature. Equation of state of an ideal gas. Mendeleev-Clayperon equation. Gas laws - isotherm, isobar, isochore
- Wave optics. Particle-wave theory of light. Wave properties of light. Dispersion of light. Interference of light. Huygens-Fresnel principle. Diffraction of light. Polarization of light
- Thermodynamics. Internal energy. Job. Quantity of heat. Thermal phenomena. First law of thermodynamics. Application of the first law of thermodynamics to various processes. Thermal balance equation. Second law of thermodynamics. Heat engines
- Electrostatics. Basic concepts. Electric charge. Law of conservation of electric charge. Coulomb's law. Superposition principle. The theory of short-range action. Electric field potential. Capacitor.
- Constant electric current. Ohm's law for a section of a circuit. DC operation and power. Joule-Lenz law. Ohm's law for a complete circuit. Faraday's law of electrolysis. Electrical circuits - series and parallel connections. Kirchhoff's rules.
- Electromagnetic vibrations. Free and forced electromagnetic oscillations. Oscillatory circuit. Alternating electric current. Capacitor in an alternating current circuit. An inductor (“solenoid”) in an alternating current circuit.
- Elements of the theory of relativity. Postulates of the theory of relativity. Relativity of simultaneity, distances, time intervals. Relativistic law of addition of velocities. Dependence of mass on speed. The basic law of relativistic dynamics...
- Errors of direct and indirect measurements. Absolute, relative error. Systematic and random errors. Standard deviation (error). Table for determining the errors of indirect measurements of various functions.
- N – number of revolutions around an axis or in a circle,
- t is the time during which they were completed.
The number of repetitions of any events or their occurrence in one timer unit is called frequency. This physical quantity is measured in hertz – Hz (Hz). It is denoted by the letters ν, f, F, and is the ratio of the number of repeating events to the period of time during which they occurred.
When an object rotates around its center, we can talk about such a physical quantity as rotation frequency, the formula:
In the SI system it is denoted as – s-1 (s-1) and is referred to as revolutions per second (rps). Other units of rotation are also used. When describing the rotation of planets around the Sun, they speak of revolutions in hours. Jupiter rotates once every 9.92 hours, while the Earth and Moon rotate every 24 hours.