Каждый магнит, который попадается нам в жизни, обладает рядом характерных черт. Главной особенностью является способность притягиваться к предметам из металла или стали. Второе качество заключается в наличии полюсов.
Проверка полюсов достигается за сет приближения одного магнита к другому. Притягиваются противоположные полюса (юг и север). Идентичные полюса отталкиваются друг от друга.
Магнитное поле
Электроны, двигаясь вокруг атома, создают магнитное поле, при этом неся отрицательный заряд. При постоянном перемещении производится электрический ток. Магнитное поле появляется за счет движения тока, сила тока влияет на силу магнитного поля.
С учетом данной информации можно сделать вывод о наличии связи между магнетизмом и электричеством. В совокупности данное явление называется электромагнетизм.
Движение электронов вокруг ядра не единственная причина появления магнитного поля. Не в меньшей степени на него влияет движение атомов вокруг своей оси. Отдельные материалы обладают магнитным полем, в котором атомы подавляют друг друга, осуществляя хаотичное движение.
Предметы из металла обладают упорядоченными группами атомов, ориентированных в определенную сторону. Благодаря способности направлять атомы в заданном направлении и складывать магнитные поля, предметы из металла способны намагничиваться.
§3. О физической сущности взаимодействия постоянных магнитов
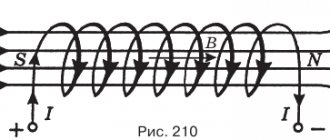
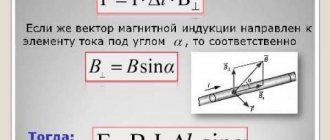
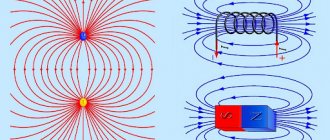
Всем известно, как взаимодействуют магниты. Они либо притягивают, либо отталкивают друг друга в зависимости от взаимного расположения их полюсов, причем это взаимодействие осуществляется без непосредственного соприкосновения магнитов друг с другом. Поэтому считают, что вокруг магнита существует свое специальное магнитное поле, отличное от поля электрического заряда. Тогда силы взаимодействия между магнитами можно рассматривать как результат взаимодействия их полей с самими магнитами, т. е. поле одного магнита действует непосредственно на другой магнит, и наоборот. По аналогии с электрическим полем считается, что существуют силовые линии у магнитного поля, тем более, что они хорошо выделяются с помощью магнитных стрелок или железных опилок (рис 1). Силовые линии указывают направление магнитного поля, которое будет расположено по касательной к силовой линии в любой точке. Направление магнитного поля в данной точке можно определить как направление, которое указывает северный полюс стрелки компаса, помещенной в эту точку, поэтому силовые линии всегда направлены от северного полюса магнита к южному. Магнитное поле в любой точке пространства можно представить вектором В, называемым магнитной индукцией, величину которого можно определить через вращающий момент, действующий на магнитную стрелку, когда она не ориентирована вдоль магнитной силовой линии (рис. 2). Чем больше момент, тем сильнее магнитное поле. Магнитная стрелка будет находиться в равновесном состоянии, когда расположится по касательной к силовой линии в данном месте. Величина магнитного поля характеризуется плотностью силовых линий, т. е. их числом на единицу площади. Однако, физическая сущность магнитного поля, как и электрического поля, остается до сих пор неизвестной, а вектор индукции В определяется опытным путем. По этой причине, очевидно, совершенно отсутствует теория взаимодействия постоянных магнитов и, как это ни удивительно, нет даже экспериментальных данных по этому взаимодействию. И это можно понять, потому что, не имея теории, невозможно анализировать результаты экспериментов. В данном параграфе производится исследование взаимодействия постоянных магнитов с помощью полей кинетической энергии, которые существую вокруг и внутри магнитов и представляют собой вихревое движение частиц вакуума, создаваемое упорядоченным движением электронов в магните. Характер магнитного поля, представляющего собой вихревое движение вакуума, с торцов и цилиндрической поверхности магнита показан на рисунке 3, причем, если смотреть на магнит с его северного полюса, вращение вакуума будет происходить по часовой стрелке, а если смотреть с южного полюса – против часовой стрелки. Такое направление вращения частиц вакуума соответствует всем экспериментам, проведенным с магнитами. Ниже это будет показано на ряде других примеров магнитных взаимодействий. В магнитном поле можно выделить несколько областей с целью их математического описания: усеченные конусы с торцов (со стороны полюсов) и часть со стороны цилиндрической поверхности. Угол при вершинах полюсов предполагается равным 900. Здесь же показана примерная эпюра распределения линейных скоростей частиц вакуума со стороны цилиндрической поверхности магнита. Следует заметить, что такой характер магнитного поля был выбран достаточно произвольно на основе картины так называемых силовых линий, образуемой железными опилками. Ниже будет показана физическая сущность этой картины. При исследовании взаимодействия магнитов со стороны полюсов будем считать, что взаимодействуют только конические области магнитных полей. Для любого поперечного сечения конуса угловую скорость вращения вакуума будем считать постоянной, зависящей только от координаты Z (рис. 4): , (1) где R- радиус магнита, — угловая скорость вакуума на торцовой поверхности магнита, — неизвестный показатель степени. Докажем постоянство угловой скорости вакуума на торцовой поверхности магнита. Поскольку магнитное поле создается вращением электронов вокруг ядра атома при их упорядоченном движении по всему объему магнита, характер движения вакуума будет зависеть от результата сложения движений частиц вакуума под воздействием отдельных электронов. На рис. 5 изображено упорядоченное движение электронов вокруг ядер атомов на некотором расстоянии r и r + 2r0 от оси магнита, где r0 — радиус орбиты электрона. Так как для большего радиуса число электронов будет больше, суммарная окружная скорость электронов для внешних атомов будет больше, чем для внутреннего слоя атомов. Разность этих скоростей может быть найдена через число атомов, расположенных на соседних окружностях: ; (2) (3) Разность числа атомов на этих окружностях равна и, следовательно, нескомпенсированная окружная скорость будет равна: , (4) где — угловая скорость вращения электрона вокруг ядра атома. Приняв и , после интегрирования выражения (4) получим: (5) Отсюда угловая скорость вращения вакуума на любом расстоянии r от оси магнита будет равна: , (6) т. е. будет постоянна и одинакова для всего объема магнита, независимо от r. Окружная же скорость частиц вакуума будет изменяться по линейному закону в зависимости от r. Что же касается , выражение (1) требует экспериментальной проверки. Выражение (6) можно было бы использовать для расчета круговой частоты вращения магнитного поля в объеме магнита, если бы все электроны вращались в одной плоскости, т. е. движение всех электронов было бы упорядоченным. Однако, так никогда не бывает, поэтому результирующая скорость вращения будет значительно меньше. Для примера рассчитаем угловую скорость вращения электрона в атоме водорода, у которого линейная скорость вращения равна, примерно км/сек, а расстояние до ядра равно м/с: Значит, для магнитного поля эта величина будет меньше. Поскольку никаких данных на этот счет нет, круговую частоту вращения следует найти из эксперимента. Правда в работе [8, с. 74] для протонного ядерно-резонансного магнитометра, в котором происходит прецессия ядер, находящихся в магнитном поле, приводится соотношение между частотой прецессии и магнитной индукцией поля В, принятое Ассамблеей МАГА в 1960 г.: Это соотношение может быть принято за отправную точку, однако действительное соотношение для твердых тел (а не водорода, как в приборе) должно быть меньше. Окружную скорость вакуума в сечении Z представим выражением (см. рис. 4): , (7) где радиус может быть найден из соотношения (при , ): (8) откуда: . (9) Тогда окружная скорость будет иметь вид: (10) где . Так как возникающее при вращении вакуума поле кинетической энергии будет неоднородным, на частичку вакуума будет действовать сила, обусловленная наличием градиента поля (сила инерции): , (11) где — кинетическая энергия элементарной массы , l — координата, характеризующая направление в пространстве, по которому берется производная от кинетической энергии. Кинетическая энергия элементарной массы определяется выражением: (12) Имея ввиду, что и , после замены переменной и дифференцирования приведем выражение (11) к следующему виду: (13) где координата l’ отсчитывается от торцовой поверхности магнита. Силы , действующие на все элементарные массы, будут суммироваться, в результате чего на торцовую поверхность магнита будет действовать сила, величина которой может быть найдена интегрированием выражения (13) после подстановки в него выражения для элементарной массы: (14) где , — плотность вакуума. Чтобы найти осевую результирующую силу, используем проекцию элементарной силы на ось магнита: (15) В результате интегрирования получим: (16) Очевидно, точно такая же сила будет действовать и на другой полюс магнита, поэтому магнит будет находиться в уравновешенном состоянии. При торцовом взаимодействии магнитов равновесие нарушится, так как с внутренней стороны объемы конических полей будут ограничены расстоянием между полюсами магнитов (рис. 6). При взаимодействии разноименными полюсами магниты будут притягиваться, одноименными отталкиваться. Такой характер взаимодействия магнитов зависит от направления относительного вращения вакуума в конусах магнитов. При одинаковом направлении вращения вакуума во взаимодействующих конусах (со стороны разноименных полюсов) силы, действующие на любой магнит, определяются полями кинетической и потенциальной энергии, причем принимается, что собственное поле магнита является полем кинетической энергии, а наложенное на него поле другого магнита- полем потенциальной энергии. Считается также, что динамическое давление в этом случае не возникает. При вращении вакуума в разные стороны (взаимодействуют одноименные полюса) принимается, что результирующее поле кинетической энергии определяется разностью собственного и наложенного полей кинетической энергии. Соответственно этому поле потенциальной энергии определится удвоенным значением поля потенциальной энергии. В этом случае возникает динамическое давление, величина которого также будет определяться удвоенным значением потенциальной энергии. Силы, определяемые полем потенциальной энергии, а также динамическим давлением берутся с отрицательным знаком. Сначала рассмотрим взаимодействие магнитов со стороны разноименных полюсов. Для упрощения расчетов возьмем цилиндрические магниты одинаковых размеров с одинаковой индукцией В, т. е. с одинаковыми угловыми скоростями на торцовых поверхностях, так как механическим аналогом индукции может быть только круговая частота движения вакуума. Значение должно быть связано с индукцией В через посредство пока неизвестного коэффициента , где коэффициент имеет размерность . Силы, действующие на внешние торцы магнитов, будут определяться выражением (16). С внутренней же стороны они определяются полями кинетической и потенциальной энергии и , которые для конуса первого магнита будут иметь вид: (17) (18) Скорости частиц вакуума для обоих магнитов в соответствии с выражением (10) представим в следующем виде: ; (19) (20) где (21) (22) Имея ввиду, что и используя выражения (21) и (22), выражение (20) преобразуем к виду: (23) Для поля кинетической энергии осевая сила определяется выражением, аналогичным выражению (16), где пределы интегрирования по взяты в пределах от 0 до : (24) Сила от поля потенциальной энергии определяется выражением (дается без вывода, так как он производится аналогично, только производная по берется с отрицательным знаком): (25) (интеграл по l’ в данном выражении будет взят ниже при выбранном значении n). Таким образом, на магнит будут действовать две силы с внутренней стороны, определяемые выражениями (24) и (25), и одна сила с внешней стороны, определяемая выражением (16). Поскольку силы от полей кинетической энергии направлены в разные стороны, результирующая сила будет равна их разности и будет прижимать магниты друг к другу. Величина этой силы будет равна: (26) Сила же от поля потенциальной энергии будет отталкивать магниты. Общая же суммарная сила будет прижимать магниты друг к другу. Рассмотрим теперь взаимодействие одноименных полюсов магнитов. Внешние силы, действующие на магниты, останутся теми же, внутренние же изменятся, так как вращение частиц вакуума в конусах будет происходить в разные стороны и энергии частиц будут вычитаться. В результате этого, как отмечалось выше, поле кинетической энергии в конусе уменьшится, поле потенциальной энергии увеличится на такую же величину, т. е. удвоится, появится также динамическое давление. Таким образом, будем иметь: (27) (28) , (29) где — динамическое давление, dV- объем элементарной массы, определяемый отношением . Выражение (29) характеризует динамическое давление на торцовой поверхности магнита (). Силы, определяемые производными от кинетической и потенциальной энергии, могут быть найдены по формулам (24) и (25), причем формулу (24) можно использовать без изменения, а для формулы (25) следует ввести множитель 3. Сила же динамического давления на торцевой поверхности магнита может быть найдена с помощью соотношений: ; (30) (31) Знак минус в выражении (31) показывает, что осевая сила от динамического давления направлена к поверхности магнита. При выводе этой формулы использовалось соотношение: . Таким образом, при взаимодействии одноименных полюсов на магнит будут действовать две отталкивающие силы и одна прижимающая- . В результате магниты будут отталкиваться. Однако, для использования полученных уравнений необходимо знать показатель степени v и круговую частоту вращения вакуума. С целью определения этих величин было проведено измерение силы притяжения между двумя одинаковыми магнитами цилиндрической формы с диаметром 24 мм и толщиной 8 мм.. Среднее значение индукции на полюсах составляло 0,265 Тл. Сила притяжения определялась для различных значений L с помощью бытового динамометра с пределом измерения до 10 кг. Затем уравнения решались при различных значениях n (1; 1,5; 2; 2,5; 3). Лучшее приближение к экспериментальным данным было получено при v=3. Формула (25) в этом случае будет представлена выражением: (32) Теоретические кривые для притяжения и отталкивания, а также экспериментальные результаты представлены на рисунке 7. Как видно из рисунка теоретические значения притяжения и отталкивания не равны друг другу, причем сила притяжения меньше. При v=2,5 сила притяжения будет больше силы отталкивания. Значения сил, очевидно, будут близки в интервале 2,5<v<3. Нами были сделаны расчеты коэффициентов для показателя степени v=2,65, результаты расчетов показаны на рисунке 8. При таком значении v, действительно, силы притяжения практически равны силам отталкивания, но расчетные кривые тем не менее не совсем совпадают с экспериментальной кривой. Это расхождение может быть следствием как неточности теории, так и неточности эксперимента, но тем не менее можно считать, что экспериментальная и расчетная кривые достаточно хорошо совпадают друг с другом. Однако следует заметить, что из предлагаемой теории ниоткуда не следует равенство сил притяжения и отталкивания. Это может быть выяснено только с помощью эксперимента. Имея экспериментальные значения силы притяжения и значения магнитной индукции можно найти круговую частоту вращения с помощью выражения: , (33) где R=1210-3 м, а значению силы F=90 Н, как это следует из рисунка 8, соответствует значение коэффициента =0,8. Следует отметить, что здесь представляет собой реальную круговую частоту магнитного поля для данного магнита. В результате получаем: Как видим, значение получилось значительно меньше предполагаемого. Данное обстоятельство можно объяснить тем, что сила со стороны вакуума, очевидно, будет действовать не на весь объем магнита, а только на составляющие его микрочастицы, которые по отношению ко всему объему занимают ничтожную часть. Поэтому предлагается относить действующую силу к объему, занимаемому ядрами атомов. Поскольку основной составляющей материала магнита является железо, формулу (33) надо умножить на коэффициент , равный отношению объема ядра атома железа к объему всего атома: где м, м. Подставив эти значения в формулу (33) найдем новую круговую частоту вращения вакуума: Отсюда можно найти значение коэффициента , устанавливающего связь между магнитной индукцией В и круговой частотой : Этот результат является вполне удовлетворительным. Для сравнения можно привести значение подобного коэффициента, который используется в протонном ядерно-резонансном магнитометре, оно равно 2,67513108 с-1/Тл [8, с. 74-75]. Теперь рассмотрим взаимодействие магнитов со стороны цилиндрических поверхностей. Для упрощения задачи будем считать, что вращение вакуума происходит в пределах длины цилиндра. Здесь возможны два варианта, когда вращение происходит в одном или в разных направлениях (рис. 9 а, б), что приводит к отталкиванию или притяжению магнитов. Появление сил притяжения и отталкивания объясняется взаимодействием полей магнитов, т.е. взаимодействием вихрей вакуума, создаваемых магнитами. При рассмотрении взаимодействующих полей можно выделить пять участков с определенным соотношением полей кинетической и потенциальной энергии, симметричных по отношению к линии раздела. При вращении вакуума в разные стороны будут следующие соотношения (рис. 10): I участок: II участок: III участок: IV участок: V участок: На участках IV и V на цилиндры будут действовать также силы от динамического давления, определяемые через . При вращении вакуума в одну сторону (рис. 11) при тех же границах участков будем иметь соотношения: I участок: II участок: III участок: IV участок: V участок: Силы от динамического давления будут действовать на I и II участках и будут определяться через . Соотношения, принятые для кинетических и потенциальных энергий, в обоих случаях определяются направлением скоростей частиц вакуума на соответствующем участке: если угол между скоростями меньше 900, кинетические энергии полей не вычитаются, если больше 900- вычитаются. Соответственно изменяются и поля потенциальной энергии. Законы изменения линейных скоростей частиц вакуума представим в виде: ; (34) , (35) где и — окружные скорости на поверхности цилиндров; и — радиусы цилиндров; и — текущие радиусы, — неизвестный показатель степени, отличающийся, очевидно, от показателя v. Так как размеры магнитов и их индукция принимаются одинаковыми, линейные скорости и радиусы будут равны (; ), а граница раздела полей будет являться осью симметрии. Имея ввиду, что (36) где l — расстояние между осями цилиндров, получим следующие выражения кинетической энергии для элементарных масс: ; (37) (38) Силы, действующие на элементарные массы и обусловленные полями кинетической () и потенциальной () энергии, определятся выражениями: ; (39) (40) где , h- длина цилиндра. Проекции результирующих сил, действующих на поверхность первого цилиндра, на межосевое расстояние L определяется интегралами: (41) (42) Здесь: и , и — начальные и конечные значения углов и радиусов на соответствующих участках. Множитель 2 введен в выражения (41) и (42) в связи с тем, что на вторую половину цилиндра от 1800 до 3600 будут действовать такие же силы, что и на первую половину. Интеграл по в выражении (41) будет равен: (43) Интеграл же по в выражении (42) удобнее брать для конкретного значения . Выражения для этого интеграла ввиду их громоздкости не приводятся. Проекция на l силы от динамического давления определяется следующим образом: (44) (45) где (46) Формулы (41), (42) и (46) используются как при вращении вакуума в одну, так и в разные стороны в соответствии с соотношением полей кинетической и потенциальной энергий на различных участках. Результаты расчетов для различных значений приведены в параграфе 11 главы IV. Величина действующих сил может быть найдена по формуле:
(47) где =11,810-15, также как и для случая взаимодействия магнитов торцевыми полями. Интересно отметить, что при любых значениях сила притяжения не равна силе отталкивания. Представляется также интересным рассмотреть взаимодействие магнитов со стороны полюсов при их относительном касательном движении (при постоянном расстоянии между полюсами). Для упрощения задачи будем считать, что их торцевые магнитные поля имеют цилиндрическую форму с радиусом магнита R и с одинаковым значением угловой скорости в любом сечении. Тогда взаимодействие полей начнется с момента их касания при движении магнитов в касательном направлении. С точки зрения особенностей взаимодействия полей можно выделить три характерные взаимные положения магнитов (рис. 12, 13, 14), при которых их межосевое расстояние лежит соответственно в пределах: 1) ; 2) ; 3) . Для каждого из этих положений будут иметь место соответствующие формулы для расчета взаимодействия. Рассмотрим первый случай взаимодействия (рис. 12). Особенностью такого взаимодействия магнитов является то, что поля частично перекрывают друг друга, причем по отношению к границе раздела поля будут взаимно меняться с основного (поле кинетической энергии) на дополнительное (поле потенциальной энергии), т. е. большее по величине поле будет считаться основным, меньшее- дополнительным. Так, например, для первого диска его поле будет основным справа от границы раздела (правый сегмент), а слева от границы- дополнительным (левый сегмент). При взаимодействии полей поля кинетической энергии магнитов будут вычитаться, а поле потенциальной энергии удваиваться, если угол между скоростями частиц вакуума будет больше 900. Если угол будет меньше 900, поля кинетической энергии не изменяются, а меньшее по величине поле становится полем потенциальной энергии. В обоих случаях динамическое давление нами не учитывалось, поскольку не ясно, на какую поверхность оно должно действовать. При вращении вакуума в одну сторону для левого сегмента кинетическая и потенциальная энергии определятся выражениями: (48) (49) Принимаем где Тогда получим: (50) (51) Соответственно элементарные силы будут равны: ; (52) (53) а их сумма определится выражением: (54) Имея ввиду, что , где h – длина магнита (поскольку силы будут действовать на микрочастицы магнита), найдем проекцию на l общей результирующей силы: (55) где . Множитель 2 введен в (55) и последующие выражения в связи с симметричностью сил, действующих на две половины круга: от 0 до 1800 и от 1800 до 3600. Для правого сегмента кинетическая и потенциальная энергии будут равны: (56) (57) Силы, определяемые этими энергиями, соответственно будут равны: (58) (59) (60) (61) где Результирующая сила, действующая на оба участка, определится суммой сил и . При вращении вакуума в разные стороны для левого сегмента будем иметь: (62) (63) (64) (65) (66) (67) где . Для правого сегмента будет: (68) (69) (70) (71) (72) (73) где . Следует заметить, что интегралы в приведенных формулах легко берутся, однако ввиду большого объема эти выражения не приводятся. При втором взаимном положении магнитов (рис. 13) можно выделить по четыре участка как справа от линии раздела (правый сегмент), так и слева от нее (левый сегмент). Поэтому при вращении вакуума в одну сторону для левого сегмента получим: I участок: (74) ; (75) (76) (77) (78) (79) где . II участок: сила будет определяться в общем виде таким же выражением как и , только пределы интегрирования будут другими: . III участок: (80) (81) (82) (83) (84) (85) где IV участок: сила определится выражением (85) с пределами интегрирования: . Для правого сегмента будем иметь: I участок: (86) (87) (88) (89) (90) (91) где II участок: сила определяется выражением (91) с пределами интегрирования: III участок: (92) (93) (94) (95) (96) (97) где IV участок: сила определится выражением (97) с пределами интегрирования: . В результате суммарная сила, действующая на первый магнит, будет складываться из восьми сил. При вращении вакуума в разные стороны для левого сегмента получим: I участок: (98) (99) (100) (101) (102) (103) где II участок: сила определится выражением (103) с пределами интегрирования: III участок: (104) (105) (106) (107) (108) (109) где IV участок: сила определяется выражением (109) с пределами интегрирования: Для правого сегмента будем иметь: I участок: (110) (111) (112) (113) (114) (115) где II участок: сила определится выражением (115) с пределами интегрирования: III участок: (116) (117) (118) (119) (120) (121) где IV участок: сила определяется выражением (121) с пределами интегрирования: В результате сила, действующая на магнит со стороны двух сегментов, определяется суммой восьми сил . При третьем относительном положении магнитов (рис. 14) левый сегмент взаимодействующих полей разбивается на пять частей, а правый на три части. При вращении вакуума в одну сторону для левого сегмента получим: I участок: (122) (123) (124) (125) (126) (127) где II участок: сила определяется выражением (127) с пределами интегрирования: III участок: (128) (129) (130) (131) (132) (133) где IV участок: сила определяется выражением (133) с пределами интегрирования: V участок: сила также определяется выражением (133) с пределами интегрирования: . Для правого сегмента будем иметь: I участок: (134) (135) (136) (137) (138) (139) где II участок: (140)
(141) (142) (143) (144) (145) где III участок: сила определяется выражением (145) с пределами интегрирования: Общая результирующая сила, действующая на первый магнит со стороны двух сегментов поля, будет равна сумме восьми сил. Для всех рассмотренных случаев взаимодействия полей были сделаны расчеты, результаты которых представлены на рисунке 15. Неожиданной является смена знака силы взаимодействия при изменении относительного расстояния как при вращении в одну, так и в другую сторону. Однако, это явление дает возможность объяснить торможение магнитного маятника в поле другого магнита. Рассмотрим колебания цилиндрического магнита диаметром 2R на подвеске длиной l в поле другого цилиндрического магнита такого же диаметра (рис. 16). Для упрощения расчетов примем, что сила взаимодействия магнитов появляется при взаимном перекрытии цилиндрических полей, т. е. начиная с расстояния 2R между осями, причем закон изменения магнитной силы представим в приближенном виде: , (146) где — амплитудное значение силы, — текущее значение угла поворота, — угол отклонения маятника, соответствующий расстоянию 2R. На рис. 16 показана эпюра и зона действия этой силы, причем на первой полуволне магнитная сила будет отталкивающей. Будем также считать, что во всех положениях магнитная сила направлена по касательной к траектории магнита. Амплитудное значение силы определим по формуле: , (147) где для данных магнитов =0,1; ; 1/с; R=м; м; кг/м3, откуда FН.! На маятник также будет действовать сила тяжести магнита G, равная 0,3 Н. Уравнение движения маятника в общем виде характеризуется уравнением: , (148) где J- момент инерции маятника относительно точки подвеса, — момент всех сил, действующих на маятник. Движение маятника можно разбить на два участка: 1) только под действием силы тяжести от угла до угла ; 2) под действием силы тяжести и силы от угла до вертикального положения . Тогда получим: 1) для первого участка: ; (149) 2) для второго участка: (150) Знак минус перед моментом от силы поставлен потому, что аргумент при изменении от до 0 изменяется от до 0 в отрицательном направлении, т. е. по часовой стрелке. На первом участке маятник под действием силы тяжести разгоняется до некоторой скорости , величина которой определяется выражением [3,с.572]: (151) при начальных условиях: ; . Решения уравнения (150) в общем виде нет. Поэтому с целью приближенного анализа движения момент от веса учитывать не будем, так как он значительно меньше момента от магнитной силы . Тогда, введя новую переменную (152) и учтя начальные условия: ; (153) , (154) найдем угловую скорость движения маятника на втором участке: , (155) где (156) Переходя к исходным обозначениям, получим: (157) Для определения угловых скоростей маятника на обоих участках зададимся длиной маятника l= 0,1 м и начальным углом отклонения . Приняв, что , где m=0,03 кг и найдя рад=13,750 по формуле (151), определим : 1/с Затем найдем значение угла , при котором скорость будет равна нулю, для чего приравняем нулю выражение под корнем в формуле (157), откуда получим: (158) Подставив значение всех величин, входящих в данное выражение, определим : , откуда и . Таким образом для данного случая взаимодействия магнитов маятник затормозится при достижении угла в 0,840, т.е. не сделает и одного полного качания. Очевидно, подобный же механизм торможения будет действовать за счет индукции при использовании медной пластины вместо неподвижного магнита. В заключение рассмотрим вопрос о так называемых магнитных силовых линиях, которые наглядно предстают перед нами в виде некоторой картины из железных опилок. Поскольку эта картина является объективной реальностью, она должна характеризовать некоторые особенности движения вакуума вокруг магнита. Общепризнанно, что магнитные силы направлены по касательным к силовым линиям. Но так ли будет на самом деле? Если частички железных опилок рассматривать как маленькие магнитики (магнитные стрелки), их положение будет определяться силами взаимодействия полей магнитиков с полем магнита. Взаимодействие магнитной стрелки с потоком вакуума можно рассматривать (по аналогии с твердым телом) путем сложения скоростей внутри объема самого магнита (см. рис. 17, а). Величина силы взаимодействия определяется выражением: , (159) где — масса вакуума в объеме магнитика; — угловая скорость вращения вакуума в магнитике; — линейная скорость частиц вакуума в поле магнита на расстоянии . На рис. 17,а показано направление силы F, возникающей при взаимодействии полей внутри магнитика, причем эта сила будет направлена против градиента суммарного поля. На рис. 17,а приняты следующие обозначения: , где — радиус магнитика (магнитик рассматривается как цилиндр); — мгновенный центр скоростей суммарного поля. На рис. 17, б показано начальное положение магнитика, центр которого отстоит от поверхности магнита на расстоянии Z, а сам магнитик расположен по направлению радиуса-вектора . При таком положении магнитика на его нижнюю половину будет действовать большая сила, а на верхнюю- меньшая. Под действием большей силы магнитик начнет поворачиваться по часовой стрелке (для данного случая) до тех пор пока силы не уравняются, что может быть только при равенстве скоростей частиц вакуума внешнего магнитного поля. Действительно, при повороте магнитика скорости частиц вакуума будут выравниваться так как ближний конец магнитика будет удаляться от магнита и приближаться к оси, а дальний- приближаться к магниту и удаляться от оси. С удалением же от поверхности магнита скорость вакуума уменьшается, а с увеличением радиуса — увеличивается. Выведем расчетные формулы для угла поворота магнитика . Из геометрических соотношений получим: ; (160) ; (161) ; (162) , (163) где — длина магнитика. Отсюда будем иметь: ; (164) ; (165) Так как , выражения (164) и (165) преобразуем к виду (поделив числитель и знаменатель на R): (166) (167) Линейные скорости частиц в крайних точках магнитика определятся выражениями (см. формулу (10)): ; (168) ; (169) где Приравняв эти скорости, получим соотношение: (170) Выражения (166), (167) и (170) используются следующим образом. Сперва задаются значениями , , , т. е. размером магнитика и координатами его центра. Затем методом подбора находятся значения угла , удовлетворяющие данным выражениям при выбранном значении n. На рис. 18 показано положение магнитиков с торцевой части исследованного нами магнита при и n=3. Как видно из рисунка картина расположения магнитиков в общем похожа на картину расположения железных опилок. Отсюда можно сделать вывод, что опилки или магнитные стрелки располагаются не по направлению силовых линий, а по линиям равных скоростей частиц вакуума, вращающегося вокруг магнита. Эти линии следует назвать изотахами. И еще следует отметить одно интересное обстоятельство: железные опилки располагаются таким образом, что они образуют четкие линии, не соприкасающиеся друг с другом. Это и дало, очевидно, основание говорить о магнитных силовых линиях. Объяснение этому явлению достаточно простое: железные опилки, как маленькие магнитики, не могут соприкасаться друг с другом, поскольку они все вращают вакуум в одну и ту же сторону и взаимодействуют с цилиндрических поверхностей на отталкивание, как это было показано выше. Используя картину расположения железных опилок вокруг магнита, можно найти значение показателя степени v, характеризующего убывание линейной скорости вакуума по мере удаления от магнита. Так, произведя преобразование выражения (170), получим формулу для экспериментального определения v на торцевой стороне магнита (со стороны полюсов): (171) Эта формула будет справедлива при постоянстве угловой скорости вращения вакуума в пределах конуса для любого поперечного сечения Z. Однако, такое предположение может в действительности и не выполняться, тогда формула (171) будет приближенной. Есть также другой независимый экспериментальный способ определения показателя степени v с помощью измерения индукции магнитного поля на различных расстояниях от поверхности магнита. Расположение датчика при двух измерениях магнитной индукции с торца магнита показано на рис. 19. Поскольку при взаимодействии магнитов предполагалась пропорциональность индукции и угловой скорости вращения вакуума, очевидно, индукция будет пропорциональна и линейной скорости частиц вакуума, если датчик будет находиться на одинаковом расстоянии от оси магнита. В этом случае можно записать следующие отношения: ; (172) , (173) где В- индукция на поверхности магнита; и — радиусы на поверхности магнита, соответствующие двум положениям датчика; и — координаты центра датчика. Радиусы и могут быть найдены из соотношений (см. рис. 19): ; (174) ; (175) Подставив эти отношения в выражения (172) и (173) и поделив первое на второе, получим: , (176) откуда после логарифмирования найдем показатель v: (177) Для исследованного нами магнита индукция на расстояниях =1 мм и =6 мм, соответственно была равна =0,265 Тл и =0,155 Тл. При R=12 мм значение v будет равно: , т. е. достаточно хорошо совпадает со значением v, найденным из силового взаимодействия. После определения v можно найти значение индукции непосредственно на поверхности магнита по одной из формул (172) или (173), например: , (178) откуда для нашего случая будем иметь: Таким образом, подводя итог всему изложенному выше, можно сказать, что предполагаемая гипотеза взаимодействия постоянных магнитов через посредство материального вакуума, несмотря на принятые допущения, достаточно хорошо объясняет природу магнетизма, причины возникновения сил притяжения и отталкивания при различных взаимных положениях магнитов, причину торможения магнитного маятника и физическую сущность магнитных силовых линий.
Приводим краткий вывод соотношения (22): откуда следует (22).
Каким образом магниты притягиваются и отталкиваются
Как притягиваются магниты? Между магнитами, поднесенными друг к другу, возникает сила. Притяжение или отталкивание магнитов ощущается не только при непосредственном контакте. Взаимодействие присутствует даже без соприкосновения.
Магниты будут отталкиваться, если поднести друг к другу их северные полюса. При контакте южных полюсов будет наблюдаться аналогичная картина. Однако, между магнитами возникнет притяжение, если к северному полюсу поднести южный. Данный принцип работает аналогично электрическим зарядам. При этом полюса магнитов и электрические заряды представляют собой разные явления.
Итог
Неодимовые магниты представляют собой изделия, которые широко используются в различных коммерческих, промышленных и бытовых областях деятельности. Этот материал имеет высокую грузоподъёмность, а также отличные свойства притягивания и большой срок службы.
Перед размагничиванием магнита из неодима, нужно убедиться в том, что имеются все необходимые для этого процесса приборы. Чтобы выполнить данный процесс должным образом, нужно использовать специальное промышленное оборудование или аппарат, способный формировать подогрев до восьмидесяти градусов плюсовой температуры.
Если изделие утратило собственные качества, то редко выполняется процесс, связанный с намагничиванием данного материального средства, так как это нецелесообразное решение. Но, когда это максимально необходимо, то заказать проведение подобного процесса можно при обращении к изготовителю.
По какой причине не все материалы способны магнититься
Магнит взаимодействует с широким перечнем веществ. Вид взаимодействия не ограничивается притяжением или отталкиванием. Отдельные металлы и сплавы обладают специфическим строением, что дает возможность притягиваться к магниту с определенной мощностью.
Другие материалы также обладают данным свойством, но в меньших масштабах. Чтобы зафиксировать притяжение в таких условиях, необходимо создание очень сильного магнитного поля. Это невыполнимо в домашних условиях. Почему свойство притяжения есть у всех материалов, а магнититься доступно для восприятия только металл? Разгадка заключается в особом внешнем строении атомов.
Окружающие нас вещи состоят из атомов, связанных между собой. Тип связи между ними определяет материал. Атомы в большинстве веществ плохо сгруппированы, поэтому связь с магнитом формируется слабая. В металле атомы хорошо скоординированы, все атомы синхронно ощущают магнитное поле и тянутся к нему.
Природа и принцип действия
Постоянные магниты – естественные вещества и прецизионные сплавы со значительной остаточной намагниченностью, которая сохраняется продолжительное время. Они изготавливаются из ферромагнитных материалов – веществ, способных сохранять намагниченность в условиях отсутствия магнитного поля, встречаются в ряде полезных ископаемых (руд). К веществам, поддающимся влиянию магнитов, относятся: железо, кобальт, никель. Сплав железа с кобальтом обладает более высоким ферромагнитными свойствами, чем каждый металл в отдельности.
Движущиеся в атоме электроны вследствие вращения формируют крохотные вихревые магнитные поля. Основу магнитного поля создаёт вращающийся вокруг собственной оси атом, как планеты, их спутники, звёзды.
Почему к постоянному магниту не притягиваются одни материалы, зато отлично «липнут» другие? Дело в направленности, ориентации магнитных линий. В немагнитных материалах (веществах с крайне слабой намагниченностью) поля атомов направляются в различные стороны, часто гася друг друга, а не усиливая.
В ряде металлов атомы структурированы, объединены в группы – домены – миниатюрные магнитики. В состоянии покоя кусок стали не обладает магнитными свойствами, а приложенное к нему поле, эти домены упорядочивает; они ориентируются в одну сторону, силовые линии складываются.