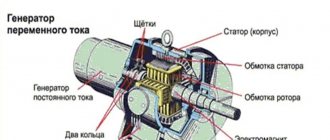
- Чем измеряют силу
Сила:
При изучения природных явлений используют разные физические величины. Для того чтобы описать качественно и количественно взаимодействие тел, вводят физическую величину, которую называют силой.
Определение силы
Сила — это физическая величина, которая служит мерой взаимодействия тел и является причиной изменения скоростей тел или их частей.
Наблюдение. Если мы рассматриваем, например, взаимодействие руки с волейбольным мячом, то мы говорим: «Мяч действует с силой на руку или рука действует с силой на мяч».
Опыт. Подвесим на пружину яблоко (рис. 66).
Пружина удлинится. Если на неё подвесить два яблока, то она удлинится больше. Итак, два яблока действуют на пружину с большей силой, чем одно.
Результат действия одного тела на другое зависит от значения приложенной силы.
Чем плотнее закрыта дверь, тем с большей силой мы должны её толкать или тянуть на себя, чтобы отворить.
Для того чтобы легче открывать дверь, её ручку прикрепляют как можно дальше от петель. Попробуйте открыть дверь, толкая её в точке, размещённой вблизи петель. Вы убедитесь, что это сделать намного труднее, чем с помощью ручки. Результат действия одного тела на другое зависит от точки приложения силы.
Для достижения определённого результата действия, например, растяжения или сжатия пружины, закрытия или открытия двери, нужно прикладывать силы в разных направлениях.
Действие одного тела на другое зависит от направления действия силы.
Графически силу изображают в виде отрезка прямой со стрелкой на конце (рис. 67).
Начало отрезка совмещают с точкой приложения силы. Длина отрезка в определённом масштабе равна значению силы. Стрелка показывает направление силы. Величины, характеризующиеся кроме числового значения еще и направлением в пространстве, называют векторными, или векторами (от латинского слова вектор — ведущий, несущий).
Почему тела изменяют свое состояние в пространстве
Любые изменения в природе происходят в результате взаимодействия между телами. Чтобы изменить положение вагона на рельсах, железнодорожники направляют к нему локомотив, который смещает вагон с места и приводит его в состояние движения (рис. 32).
Парусник может длительное время стоять возле берега до тех пор, пока не подует попутный ветер и подействует на его паруса (рис. 33). Колеса игрушечного автомобиля могут вращаться с любой скоростью, но игрушка не изменит своего положения, если под игрушку не положить дощечку или линейку (рис.34). Форму или размер пружины можно изменить, лишь подвесив к ней груз или потянув рукой за один из его концов.
Все тела в природе так или иначе связаны между собой и действуют друг на друга или непосредственно, или через физические поля. Такое действие всегда является взаимным. Если тепловоз действует на вагон и изменяет его скорость, то скорость тепловоза при этом также изменяется благодаря обратному действию вагона. Солнце действует на все тела на Земле и на саму Землю, удерживая ее на орбите. Но и Земля притягивает Солнце и, в свою очередь, изменяет его траекторию. Таким образом, во всех случаях можно говорить только о взаимном действии тел — взаимодействии.
При взаимодействии могут изменяться скорости тел или их частей.
Однако, взаимодействуя с различными телами, данное тело будет изменять свою скорость по-разному. Так, парусник может приобрести скорость вследствие действия на него ветра. Но такой же результат можно получить, включив двигатель, который находится на паруснике. Парусник может сдвинуть с места и катер, действуя на него через трос. Чтобы каждый раз не называть все взаимодействующие тела, все эти действия объединяют одним понятием силы.
Международная система единиц и Ньютон
Под этим названием понимают систему мер и величин, которая кратко обозначается СИ (с франц. Système International). В ее основу положены 7 основных физических величин (ампер, кельвин, секунда, кандела, килограмм, метр и моль). СИ была принята в 1960 году, а в 1971 году в нее была добавлена последняя фундаментальная величина «моль».
В системе СИ единица измерения силы — ньютон. Под ним понимают такую категорию, которая, действуя на тело с массой 1 кг, ускоряет его движение на 1 м/с за каждую секунду времени. В русском языке принято обозначение ньютона [Н], на латинице же оно записывается как [N].
Применение утвержденных в СИ приставок к основным единицам измерения позволяет получить их дробные или большие значения. Для силы это могут быть, например, мкН (микроньютон, 1 мкН = 10-6 Н), мН (миллиньютон, 1 мН = 10-3 Н) или кН (килоньютон, в ньютонах это 1000 Н).
Любопытно отметить, что ньютон не входит в число 7 фундаментальных единиц измерения силы в системе СИ, поэтому он является производной единицей. В частности, 1 [Н] = 1 [кг*м/с2], то есть он выражается через килограмм (масса), метр (расстояние) и секунду (время).
Форсируем тему
В окружающем нас мире нельзя избежать встречи с силами: силы используются для открытия двери, нажатия клавиш клавиатуры, управления автомобилем, подъема по ступенькам лестницы к Статуе Свободы, вытаскивания кошелька из кармана, разговора и даже для дыхания. Силы незримо присутствует всюду: во время пешеходной прогулки, катании на коньках, пережевывании хот-дога, открывании бутылки или моргании ресниц вашей ненаглядной спутницы. Сила неразрывно связана с движением объектов, а физика помогает понять, как эта связь работает.
Сила — это на самом деле довольно забавная тема. Как и другие физические темы, она кажется сложной только до настоящего знакомства с ней. Как наши старые “друзья”, перемещение, скорость и ускорение (см. главы 3 и 4), сила является вектором, т.е. имеет величину и направление.
Сэр Исаак Ньютон первым включил силу, массу и ускорение в одно уравнение в XVII веке. (Помните исторический анекдот с падением яблока на его голову, в результате чего он якобы придумал, как математически описать силу тяготения. Подробнее об этом рассказывается в главе 6, где Ньютон также является одним из основных действующих лиц.)
Законы Ньютона и скорость света
Законы Ньютона были пересмотрены Альбертом Эйнштейном в его теории относительности. В ней было показано, что законы Ньютона не выполняются для движения со скоростью, близкой к скорости света. Основная идея теории относительности заключается в том, что скорость света является наибольшей возможной скоростью. Это значит, что любое взаимодействие может происходить только с этой или меньшей скоростью. Следовательно, при приближении к этой скорости нужно учитывать изменяющийся характер взаимодействия; Например, измерение длины ракеты, движущейся со скоростью света, будет отличаться от измерения длины неподвижной ракеты. Как будет показано в главе 21, теория относительности Эйнштейна в значительной степени изменила представленный Ньютоном взгляд на мир и его законы.
Как часто происходит со многими физическими открытиями, Ньютон сначала внимательно наблюдал за поведением объектов, мысленно моделировал его, а затем выразил в математической форме. Зная основные сведения о векторах (которые изложены в главе 4), эта математика не вызовет у вас никаких трудностей.
Ньютон описал свою модель с помощью трех утверждений, которые теперь называются законами Ньютона. Однако нужно помнить, что на самом деле это не окончательные “законы природы”, ведь физики могут создавать лишь модели природы, которые часто впоследствии пересматриваются и уточняются.
Тяжелее — Легче
Вес тела ${\large P}$ выражается произведением его массы ${\large m}$ на ускорение силы тяжести ${\large g}$.
${\large P = m \cdot g}$
Когда на земле тело становится легче (слабее давит на весы), это происходит от уменьшения массы. На луне все не так, уменьшение веса вызвано изменением другого множителя — ${\large g}$, так как ускорение силы тяжести на поверхности луны в шесть раз меньше чем на земле.
масса земли = ${\large 5,9736 \cdot {10^{24}}\ kg }$
масса луны = ${\large 7,3477 \cdot {10^{22}}\ kg }$
ускорение свободного падения на Земле = ${\large 9,81\ m / c^2 }$
ускорение свободного падения на Луне = ${\large 1,62 \ m / c^2 }$
В результате произведение ${\large m \cdot g }$, а следовательно и вес уменьшаются в 6 раз.
Но нельзя обозначить оба эти явления одним и тем же выражением «сделать легче». На луне тела становятся не легче, а лишь менее стремительно падают они «менее падучи»))).
Траектории частиц
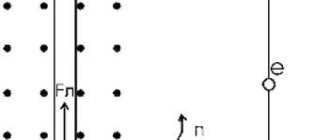
Взаимодействие магнитного поля с зарядом широко используется в масс-спектрографах при исследовании элементарных частиц.
Действие поля при этом вызывает появление силы, названной силой Лоренца. При попадании в магнитное поле движущейся с некоторой скоростью заряженной частицы формула которой имеет вид F = vBqsinα, вызывает движение частицы по окружности.
В этой математической модели v — модуль скорости частицы, электрический заряд которой — q, В — магнитная индукция поля, α — угол между направлениями скорости и магнитной индукции.
Частица движется по окружности (либо дуге окружности), так как сила и скорость направлены под углом 90 ° друг к другу. Изменение направления линейной скорости вызывает появление ускорения.
Правило левой руки, рассмотренное выше, имеет место и при изучении силы Лоренца: если левую руку расположить таким образом, чтобы вектор магнитной индукции входил в ладонь, четыре пальца, вытянутых в линию, были направлены по скорости положительно заряженной частицы, то отогнутый на 90 ° большой палец покажет направление действия силы.
Центр масс
Точка центра масс замечательна тем , что если на частицы образующие тело (неважно будет ли оно твердым или жидким, скоплением звезд или чем то другим) действует великое множество сил (имеются ввиду только внешние силы, поскольку все внутренние силы компенсируют друг друга), то результирующая сила приводит к такому ускорению этой точки, как будто в ней вся масса тела ${\large m}$.
Положение центра масс определяется уравнением:
${\large R_{c.m.} = \frac{\sum m_i\, r_i}{\sum m_i}}$
Это векторное уравнение, т.е. фактически три уравнения — по одному для каждого из трех направлений. Но рассмотрим только ${\large x}$ направление. Что означает следующее равенство?
${\large X_{c.m.} = \frac{\sum m_i\, x_i}{\sum m_i}}$
Предположим тело разделено на маленькие кусочки с одинаковой массой ${\large m}$, причем полная масса тела равна будет равна числу таких кусочков ${\large N}$, умноженному на массу одного кусочка, например 1 грамм. Тогда это уравнение означает, что нужно взять координаты ${\large x}$ всех кусочков, сложить их и результат разделить на число кусочков. Иными словами, если массы кусочков равны то ${\large X_{c.m.}}$ будет просто средним арифметическим ${\large x}$ координат всех кусочков.
| центр масс сложного тела лежит на линии, соединяющей центры масс двух составляющих его частей |
Проблемы плазмы
Взаимодействие магнитного поля и вещества используется в циклотронах. Проблемы, связанные с лабораторным изучением плазмы, не позволяют содержать ее в замкнутых сосудах. Высоко может существовать только при высоких температурах. Удержать плазму в одном месте пространства можно посредством магнитных полей, закручивая газ в виде кольца. Управляемые можно изучать, также закручивая высокотемпературную плазму в шнур при помощи магнитных полей.
Пример действия магнитного поля в естественных условиях на ионизированный газ — Полярное сияние. Это величественное зрелище наблюдается за полярным кругом на высоте 100 км над поверхностью земли. Загадочное красочное свечение газа пояснить смогли лишь в ХХ веке. Магнитное поле земли вблизи полюсов не может препятствовать проникновению солнечного ветра в атмосферу. Наиболее активное излучение, направленное вдоль линий магнитной индукции, вызывает ионизацию атмосферы.
Закон тяготения
Каждый объект Вселенной притягивается к любому другому объекту с силой, пропорциональной их массам и обратно пропорционально квадрату расстояния между ними.
${\large F = G \cdot \dfrac {m \cdot M}{R^2}}$
Добавить можно, что любое тело реагирует на приложенную к нему силу ускорением в направлении этой силы, по величине обратно пропорциональным массе тела.
${\large G}$ — гравитационная постоянная
${\large M}$ — масса земли
${\large R}$ — радиус земли
${\large G = 6,67 \cdot {10^{-11}} \left ( \dfrac {m^3}{kg \cdot {sec}^2} \right ) }$
${\large M = 5,97 \cdot {10^{24}} \left ( kg \right ) }$
${\large R = 6,37 \cdot {10^{6}} \left ( m \right ) }$
В рамках классической механики, гравитационное взаимодействие описывается законом всемирного тяготения Ньютона, согласно которому сила гравитационного притяжения между двумя телами массы ${\large m_1}$ и ${\large m_2}$, разделённых расстоянием ${\large R}$ есть
${\large F = -G \cdot \dfrac {m_1 \cdot m_2}{R^2}}$ Здесь ${\large G}$ — гравитационная постоянная, равная ${\large 6,673 \cdot {10^{-11}} m^3 / \left ( kg \cdot {sec}^2 \right ) }$. Знак минус означает, что сила, действующая на пробное тело, всегда направлена по радиус-вектору от пробного тела к источнику гравитационного поля, т.е. гравитационное взаимодействие приводит всегда к притяжению тел. Поле тяжести потенциально. Это значит, что можно ввести потенциальную энергию гравитационного притяжения пары тел, и эта энергия не изменится после перемещения тел по замкнутому контуру. Потенциальность поля тяжести влечёт за собой закон сохранения суммы кинетической и потенциальной энергии, что при изучении движения тел в поле тяжести часто существенно упрощает решение. В рамках ньютоновской механики гравитационное взаимодействие является дальнодействующим. Это означает, что как бы массивное тело ни двигалось, в любой точке пространства гравитационный потенциал и сила зависят только от положения тела в данный момент времени.
Принцип суперпозиции
Опыт показывает, что если на данное тело действуют несколько других тел, то соответствующие силы складываются как векторы. Более точно, справедлив принцип суперпозиции. Принцип суперпозиции сил. Пусть на тело действуют силы ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$ Если заменить их одной силой ${\large \overrightarrow{F} = \overrightarrow{F_1} + \overrightarrow{F_2} \ldots + \overrightarrow{F_n}}$, то результат воздействия не изменится. Сила ${\large \overrightarrow{F}}$ называется равнодействующей сил ${\large \overrightarrow{F_1}, \overrightarrow{F_2},\ \ldots \overrightarrow{F_n}}$ или результирующей силой.
Примеры использования
При средней гравитации на Земле (условно, g = 9,806 65 м / с2) масса 1 килограмма оказывает силу около 9,8 ньютона. Яблоко среднего размера предполагает около одного ньютона силы, которую мы измеряем как вес яблока.
1 N = 0,10197 кг × 9,80665 м / с2 (0,101 97 кг = 101,97 г)
Вес среднего взрослого человека прилагает силу около 608 Н.
608 N = 62 кг × 9,80665 м / с2 (где 62 кг — средняя масса взрослого человека в мире)
Вес тела
Да, не удивляйся, вес тела — это тоже сила, с которой тело давит на опору или какой-либо подвес (если тело висит).
Ты уже знаешь, что все тела притягиваются к Земле, и эта сила называется силой тяжести. Посмотри внимательно на картинку. В данном случае лавочка не позволяет мальчику и коту упасть, и именно лавочка испытывает действие силы, возникающей из-за притяжения Земли.
Вес тела — это сила, с которой любое тело действует на опору или подвес благодаря земному притяжению