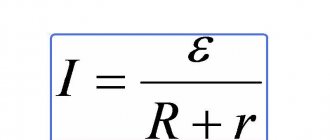Катушка Индуктивности в Цепи Переменного Тока: Принцип Действия

Теоретика

Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней.

Что такое катушка индуктивности

Разнообразие размеров катушек

Катушка индуктивности – это радиоэлемент, применяющийся в разных схемах для следующего:

Сглаживание биений;
Подавление помех;
Ограничение переменного тока;
Накопление энергии и прочее.

Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника. Деталь обладает относительно малой емкостью и малым активным сопротивлением, при этом у него имеет высокая индуктивность, то есть способность возникновения ЭДС (электродвижущей силы) в проводнике, при протекании в цепи электрического тока.

Дроссели на печатной плате

Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.

Соленоид

Бывают также и цилиндрические катушки индуктивности, называемые соленоидами. Длина такого цилиндра в несколько раз превышает его диаметр.

Интересно знать! Магнитное поле внутри соленоида однородно. Данное магнитное поле может выполнять механическую работу, втягивая ферритовый сердечник.

Обмотка с втягивающего реле на стартере

Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.

Схема сверхпроводящего индуктивного накопителя

Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.

Конструкционные особенности

Строение катушки индуктивности

Конструкционно катушка индуктивности представляет собой намотанную по спирали или винтом изолированную одножильный или многожильный проводник (чаще, лакированная медная проволока), вокруг диэлектрического сердечника (каркаса). Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.

Существуют и катушки, вовсе не имеющие сердечника, или же он является регулируемым, что позволяет менять индуктивность детали.

Тороидальная катушка

Намотка проводника может быть как однослойной, ее еще называют рядовой с шагом, или многослойной (применяются названия универсал, внавал, рядовая). Расстояние между витками называется шагом.

Интересно знать! Шаг намотки может быть прогрессивным, то есть его величина изменяется по длине катушки. Применяется такая намотка для снижения «паразитной» емкости.

Применение

Используются катушки в схемах обработки сигналов и аналоговых схемах. В сочетании с конденсаторами и прочими радиокомпонентами могут формировать участки схем, которые усиливают или отфильтровывают определенные сигналы.

Широко применяются дроссели в источниках питания, где они вместе с конденсаторами фильтра призваны устранить остаточные помехи и прочие колебания, возникающие на выходе.

Строение трансформатора

Если две катушки соединить одним магнитным полем, то получится трансформатор – устройство, способное передавать электричество от одной части цепи к другой, за счет электромагнитной индукции, попутно меняя величину напряжения.

Для справки! Трансформаторы способны функционировать только с переменным током.

Основные характеристики катушек индуктивности

Прежде чем разбираться с тем, как ведет себя ток, проходя в цепи через катушку индуктивности, давайте сначала узнаем главные характеристики этого элемента.

Определение индуктивности: формула

Прежде всего, нас интересует индуктивность – значение, численно выражающаяся соотношением потока магнитного поля, которое создается протекающим током, к силе этого самого тока. Измеряется этот параметр в Генри (Гн).
Если говорить более простым языком, то это явление можно описать так. При протекании тока через катушку индуктивности создается электромагнитное поле, которое напрямую связано с ЭДС, которая оказывает противодействие изменению переменного напряжения, то есть в цепи возникает ток, который течет в обратном направлении основному.
Измерение силы тока на катушке индуктивности и переменного напряжения, противостоят данной силе, точнее наоборот. Это свойство элемента называется индуктивным сопротивлением, которое находится в противофазе реактивному емкостному сопротивлению конденсатора, включенному в цепь переменного тока.

Совет! Изменение величины индуктивности катушки происходит пропорционально изменению числа витков.

Расчет энергии магнитного поля катушки

Давно известно, что любое магнитное поле обладает некоторой энергией. Отсюда следует, что магнитное поле катушки тоже имеет определенный запас магнитной энергии. Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.

Гидротурбина

Чтобы было еще понятнее давайте сравним катушку с гидротурбиной. Итак, водяной поток, который направлен через турбину, будет ощущать ее сопротивление, пока турбина до конца не раскрутится. Она имеет некоторую инерцию, а значит, будет вращаться синхронно с потоком воды, не оказывая ему практически никакого сопротивления.
Если вы попробуете остановить поток воды или сменить его направление, то увидите, что турбина продолжит вращаться по инерции, заставляя двигаться воду в прежнем направлении. Чем выше инерция у турбины, тем сильнее она будет сопротивляться изменению направления потока воды.
Ровно то же самое происходит в катушке индуктивности, когда переменный ток начинает течь в обратном направлении.

При последовательном соединении катушек их индуктивность складывается

Влияние тока на индуктивность катушки выражается не только в виде основного эффекта взаимодействия. Часто наблюдаются паразитные эффекты, из-за которых сопротивление переменному току катушки индуктивности чисто реактивным назвать нельзя. Из-за этих эффектов в катушке возникают некоторые потери, оценивающиеся как сопротивление потерь. Данное значение составляет сумму потерь в сердечнике, проводе, экране и диэлектрике.
Каждая из потерь вызвана разными причинами. В проводах их целых три: они обладают хоть и малым, но все же активным омическим сопротивлением; данное сопротивление растет с увеличением частоты, что обусловлено уменьшением амплитуды электромагнитных волн, по мере того как они проникают в глубину проводящей среды (это явление называется скин-эффектом) – другими словами, ток вытесняется на верхние слои провода, из-за чего изменяется площадь проводника, а значит, и его сопротивление; если провода свиты в спираль, возникает эффект близости, из-за которого тоже меняется активное сечение проводника, и общее сопротивление.

Дроссель сварочного аппарата

Потери в диэлектрике могут возникать из-за межвиткового конденсатора, или по причине его электромагнитных свойств. Однако справедливости ради стоит отметить, что потери в этой части детали настолько малы, что ими часто пренебрегают при расчетах.
Потери на сердечнике складываются из двух величин: потери на перемагничивание ферромагнетика (потери на гистерезис) и потери на вихревые токи. Переменное магнитное поле, возникающее от протекающего в проводнике тока, индуцирует вихревые ЭДС в соседних проводниках – сердечнике, проводах ближайших витков, и даже экране. Возникшие токи, имеющие название помимо вихревых, токи Фуко, также являются причиной потерь, из-за активного сопротивления провода.
С потерями на сопротивление связана и другая характеристика, называемая добротностью. Ее величина – это соотношение реактивного и активного сопротивления катушки индуктивности.

Паразитная емкость катушки индуктивности

Следующий параметр – это паразитная емкость. Явление состоит в том, что между витками катушки возникает некоторая нежелательная емкостная связь.
ТКИ (температурный коэффициент индуктивности) – все мы знаем, что при нагревании вещества увеличиваются в размерах. Когда это происходит с катушкой, мы получаем нестабильность индуктивности, из-за изменения длины и диаметра проводника, длины и диаметра каркаса, а значит, изменения диаметра и шага витков. Помимо этого перемена температуры влияет на диэлектрическую проницаемость материала каркаса, что влечет изменение емкости катушки и влияет на проницаемость магнитным полем ферромагнетика сердечника.
ТКД (температурный коэффициент дробности) – тут все понятно! Это изменение параметров добротности в зависимости от температуры.

Устройство катушки

Катушку изготавливают путем наматывания на цилиндрический или тороидальный каркас провода в изоляции. Изоляция — обязательный атрибут, без нее из-за межвиткового замыкания, катушка превратится в обычный проводник.

На концах намотанного провода устанавливают контакты. С их помощью катушка индукции подключается в цепь последовательно с нагрузкой. Внутрь каркаса может помещаться металлический сердечник.

При изготовлении катушки провод наматывают двумя способами:

в один слой: такую обмотку называют «рядовой с шагом»;
в несколько слоев: способ обозначают терминами «внавал» или «универсал».

Расстояние, на которое витки провода отстоят друг от друга, называется шагом. При намотке некоторых катушек шаг постепенно увеличивают (прогрессивный шаг), чем добиваются снижения паразитной емкости.

Включение катушки индуктивности в цепи с постоянным и переменным током

В целом, мы определили, что такое катушка индуктивности, для чего она нужна, и какие характеристики для расчета ее параметров важны, однако до сих пор неискушенному читателю наверняка не понятно, как будут изменяться параметры протекающего через эту деталь тока.

Цепь, питаемая постоянным током

Катушка индуктивности в цепи постоянного тока

Чтобы упростить изложение, будем проводить очень простой опыт:

Для начала нам потребуется блок питания, способный выдавать стабильные 12 Вольт напряжения на выходе, 12-ти вольтовая лампочка накаливания для создания сопротивления, а также сама катушка индуктивности.

Стержень из феррита

Катушку мы соберем своими руками из куска лакированной медной проволоки и ферритового стержня.

Изготовление катушки индуктивности

Инструкция предельно проста — берем проволоку и наматываем ее на стержень, после чего зачищаем ножом концы, чтобы можно было подсоединить клеммы от блока питания и подпаять провода.
Цена такой схемы минимальна, так что можете без проблем повторить опыт при желании дома.

Измерение индуктивности собранной катушки

При помощи LC-метра измеряем индуктивность полученной детали. Как видно из фото выше, в рассматриваемом примере она составила 132 мкГн.

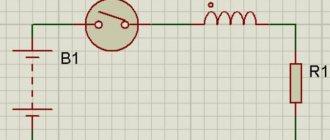
Схема с включенной катушкой индуктивности

Теперь берем все наши детали и соединяем их по приведенной выше схеме.

Схема включена в сеть

Вот что получилось на практике. Как видим, постоянный ток протекает через катушку практически беспрепятственно, если не учитывать естественное сопротивление проводника, ведь ток не меняет своего направления на противоположное.

На данной схеме лампочку заменяет резистор, но это не важно

Значит ли это, что катушка индуктивности неприменима в цепях с постоянным током? Вовсе нет! Вот другая схема, в которую, как мы видим, уже включен некий выключатель, способный размыкать цепь. Именно в момент замыкания и происходит самое интересное.
Поскольку до этого ток был равен нулю, он начнет изменяться и расти, из-за чего изменится магнитное поле катушки, что в свою очередь приведет к возникновению ЭДС. В катушке появится индукционный ток, который потечет в обратном направлении основного потока от источника питания.
Именно в момент включения величина ЭДС будет максимальной, так как скорость изменения тока в этот момент наиболее высока, а значит, ток катушки индуктивности равен нулю.
Что произойдет дальше? А дальше мы увидим, что ток в катушке индуктивности начнет расти, тогда как ЭДС, наоборот, снижаться. Вот как это выглядит на графике.

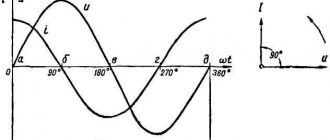
Uвх – входное напряжение питания; Il- изменение величины тока; Ul – напряжение на катушке

На верхнем графике изображено изменение напряжения входной сети, сразу после включения. Как видим, моментально появляется постоянное значение.
Дальше показано, как меняется величина тока, протекающего через катушку. Он тоже достигает постоянно значения, но не сразу, а спустя какое-то время.
Напряжение на катушке (нижний график) также вырастает моментально, но тут же начинает падать. При этом обратите внимание, что графики силы тока и напряжения зеркально противоположны.
Если все это перенести на наш опыт с лампой, то мы увидим, что после соединения цепи через выключатель, она загорится не сразу, а с некоторой задержкой.

Похожая ситуация будет и при размыкании цепи.

Физические процессы в катушке при размыкании цепи

По графикам видна противоположная ситуация, означающая, что лампочка продолжить гореть еще какое-то время после размыкания цепи.

Дело в том, что при прекращении подачи питания, в катушке снова возникнет ЭДС, однако ток индукции потечет теперь в том же направлении, что и от источника питания, то есть запасенная энергия в катушке, поддержит питание цепи.

Индуктивное сопротивление

Из выражений следует, что максимальное значение, напряжения и равное ему максимальное значение э. д. с.

м =
EL
м=
L
ω
I
M

Разделив написанные выражения на √2, получим действующие значения напряжения и э. д. с.

=
EL
=
L
ω
I
откуда действующее значение тока I

=
U
: ω
L
=
U
:
x
L

Величина, определяемая отношением напряжения к току цепи:

:
I
=ω
L
= 2π
fL
=
x
L

называется реактивным сопротивлением индуктивности или просто индуктивным сопротивлением.

Индуктивное сопротивление пропорционально индуктивности и частоте переменного тока. При изменении частоты от f

= 0 (постоянный ток) до
f =
∞ оно изменяется от
x
L = 0 до
xL
= ∞.

Маркировка

Для обозначения номинала катушки индуктивности используют буквенную или цветовую маркировку. Есть два вида буквенной маркировки.

Обозначение в микрогенри.
Обозначение набором букв и цифр. Буква r – используется вместо десятичной запятой, буква в конце обозначения обозначает допуск: D = ±0.3 нГн; J = ±5%; К = ±10%; М = ±20%.

Цветовую маркировку можно распознать аналогично таковой на резисторах. Воспользуйтесь таблицей, чтобы расшифровать цветные полосы или кольца на элементе. Первое кольце иногда делают шире остальных.

На это мы и заканчиваем рассматривать, что собой представляет катушка индуктивности, из чего она состоит и зачем нужна. Напоследок рекомендуем посмотреть полезное видео по теме статьи:

Влияние числа витков и способа намотки

Катушка индуктивности – это спираль, созданная из проводящего материала. Рабочие параметры изделий будут зависеть от особенностей конструкции. Индуктивность увеличивают:

большим количеством витков на единицу длины;
укрупнением поперечного сечения;
установкой в центральной части сердечника с ферромагнитными характеристиками.

От чего зависит индуктивность катушки, примеры типовых решений

Индуктивность одновиткового контура и индуктивность катушки

Для расчета элементарной конструкции подойдет преобразованная первая формула:

Ф = L * I.

Если рассматривается катушка, это выражение трансформируют в суммарное выражение магнитных потоков (Ψ), образованных отдельными витками:

Ψ = n * Ф.

Аналогичным образом:

Ln = L1 * n.

В действительности для точных расчетов учитывают различия силовых линий в центральной части и на краях конструкции. Для коррекции применяют более сложные выражения.

Индуктивность соленоида

Достаточно длинная электрическая катушка формирует внутри параллельные силовые линии. Для создания равномерного распределения энергии необходимо применять проводник с толщиной намного меньше, по сравнению с диаметром поперечного сечения. Разумеется, необходимо установить одинаковое расстояние между отдельными витками.

Такую конструкцию называют соленоидом. Плотность магнитного потока (B) в центральной рабочей части будет зависеть прямо пропорционально от длины (l) и следующих параметров:

количества витков (N);
тока (i);
плотности намотки (n – число контуров на единицу длины);
площади поперечного сечения (S);
объема (V = S * l).

Ниже приведены основные формулы для вычислений при отсутствии сердечника с учетом магнитной постоянной (m ≈ 1,257 *10-6 Гн/ м):

В = m0 * N * (i/l) = m0 * n * I;
Ψ = m0 * N2 * (I * S/l) = m0 * n2 * i *V;
L = m0 * N2 * (S/l) = m0 * n2 * V.

Индуктивность тороидальной катушки (катушки с кольцевым сердечником)

Для вычисления индукции катушки с сердечником в представленные выше формулы добавляют корректирующий множитель «m». С учетом особой формы изделия необходимо сделать следующие изменения:

L = N2 * ((m0 * m * S)/2π * rL), либо L = N2 * ((m0 * m * h)/2π) * ln(R/r),

где:

2π * rL – длина рабочего элемента со средним радиусом rL;
R (r) и h – наружный (внутренний) радиус и высота тора, соответственно.

Коэффициентом «m» учитывают относительный показатель магнитной проницаемости определенного материала к значению для нейтральной среды (вакуума). Если m намного больше единицы, допускается не учитывать искажения поля, которые создает толстый проводник.

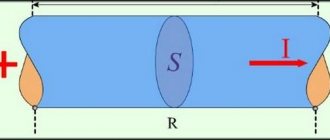
Индуктивность — проводник

Индуктивность проводников Ь зависит от их формы и размеров.

Индуктивность проводника в данной среде определяется исключительно его размерами и формой. Индуктивность прямолинейного провода невелика. Индуктивность того же провода в форме витка значительно больше. При одинаковых размерах катушек ( длин и диаметров) их индуктивность пропорциональна квадрату числа витков. Индуктивность катушки прямо пропорциональна магнитной проницаемости ia сердечника.

Индуктивность проводника зависит от его формы, размеров, а также от свойств окружающей среды. Если сила тока изменяется со временем, то изменяется и магнитный поток, сцепленный с контуром. Изменение магнитного потока, в свою очередь, вызывает появление в проводнике индукционного тока. Так как индукционный ток вызван изменением силы тока в самом проводнике, то данное явление возникновения индукционного тока называется самоиндукцией, а возникающая эдс — эдс самоиндукции. Самоиндукция является частным случаем явления электромагнитной индукции.

Индуктивность проводника численно равна магнитному потоку, создаваемому током в 1 ампер, протекающему по данному проводнику.

Индуктивность проводника характеризует его размеры и форму, а также магнитную проницаемость среды, окружающей проводник. Индуктивность проводника остается постоянной, если не изменяется его форма, размеры и магнитная проницаемость окружающей его среды.

Индуктивность проводников проявляется только при прохождении через них изменяющегося со временем тока. В этой работе индуктивность определяется методом мостика, питаемого переменным током.

Индуктивность проводника L называется еще коэффи циентом самоиндукции.

Индуктивность проводников I, зависит от их формы и размеров.

Индуктивность L проводника определяется его формой, размерами, взаимным расположением отдельных его частей, средой, в которой происходит замыкание магнитного потока.

Индуктивность проводников L зависит от их формы и размеров.

Эффект близости.

Индуктивность проводника конечного сечения складывается из внешней и н д у к-тивности.

Параметры проводника длиной 100 мм.

Если индуктивность проводника, соединяющего экран с шасси ( корпусом), велика, то экран может не уменьшить, а увеличить емкостную паразитную связь.

Соединение катушек при наличии взаимного влияния их магнитных полей.

Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше формула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:

Магнитные потоки обеих катушек имеют одинаковые направления
Магнитные потоки обеих катушек направлены навстречу друг другу

Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений токов в них.

Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.

Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответствовать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.

Разберем первый случай, когда магнитные потоки направлены в одну сторону. Очевидно, при этих условиях витки каждой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в другой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых составлена цепь.

Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.

Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по формуле:

В первом случае ставится знак + (плюс), а во втором случае знак — (минус).

Величина М, называемая коэффициентом взаимной индукции, представляет собой добавочную индуктивность, обусловленную частью магнитного потока, общей для обеих катушек.

На явлении взаимоиндукции основано устройство вариометров. Вариометр состоит из двух катушек, общая индуктивность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передатчиков.

Что такое индуктивность

Что такое индуктивность — это физическая величина, которая рассказывает нам о магнитных свойствах электрической цепи. Индуктивность измеряют в Гн (Генри).

Если вы вообще не понимаете о чём речь, то советую ознакомиться сначала с вот с этой статьей.

В электрических схемах например, нам встречаются какие-то непонятные катушки, дроссели и многие даже не знают их функциональную роль. В этой статье я постараюсь доступным языком рассказать, что такое индуктивность и как это явление применить на своей любимой работе.

Давайте посмотрим на рисунок

Давайте начнём движение проводника в магнитном поле таким образом, чтобы он пересек силовые линии постоянного магнита. Если это условие выполняется, то тогда в нашем проводнике появляется электродвижущая сила (ЭДС). Или наоборот проводник остаётся на месте, а магнит передвигают таким образом, чтобы силовые линии магнита пересекали проводник. Сейчас был пример электромагнитной индукции. Значение индуцированной электродвижущей силы в проводнике прямо пропорциональна магнитной индукции поля, скорости перемещения и длине проводника

Направление возникшей электродвижущей силы в проводнике определяют через правило правой руки.

Правая рука находится в таком положении чтобы силовые линии магнита заходили в ладонь. Следовательно, большой палец показывает нам направление перемещения проводника, а остальные пальцы покажут нам направление возникшей электродвижущей силы.

Для усиления электродвижущей силы индукции применяют электрические катушки

А если подать напряжение на катушку, то по её виткам потечёт ток, который создаёт своё магнитное поле.

Теоретическое обоснование

Если в проводящем контуре течёт ток, то ток создаёт магнитное поле.

Будем вести рассмотрение в квазистатическом приближении, подразумевая, что переменные электрические поля достаточно слабы либо меняются достаточно медленно, чтобы можно было пренебречь порождаемыми ими магнитными полями.

Ток считаем одинаковым по всей длине контура (пренебрегая ёмкостью проводника, которая позволяет накапливать заряды в разных его участках, что вызвало бы неодинаковость тока вдоль проводника и заметно усложнило бы картину).

По закону Био — Савара — Лапласа, величина вектора магнитной индукции, создаваемой некоторым элементарным (в смысле геометрической малости участка проводника, рассматриваемого как элементарный источник магнитного поля) током в каждой точке пространства, пропорциональна этому току. Суммируя поля, создаваемые каждым элементарным участком, приходим к тому, что и магнитное поле (вектор магнитной индукции), создаваемое всем проводником, также пропорционально порождающему току.

Рассуждение выше верно для вакуума. В случае присутствия магнитной среды (магнетика) с заметной (или даже большой) магнитной восприимчивостью, вектор магнитной индукции (который и входит в выражение для магнитного потока) будет заметно (или даже во много раз) отличаться от того, каким бы он был в отсутствие магнетика (в вакууме). Мы ограничимся здесь линейным приближением, тогда вектор магнитной индукции, хотя, возможно, возросший (или уменьшившийся) в заметное количество раз по сравнению с отсутствием магнетика при том же контуре с током, тем не менее остаётся пропорциональным порождающему его току.

Тогда магнитный поток, то есть поток поля вектора магнитной индукции:

Φ=∫SB⋅dS{\displaystyle \Phi =\int \limits _{S}\mathbf {B} \cdot \mathbf {dS} }

через любую конкретную фиксированную поверхность S

(в частности и через интересующую нас поверхность, краем которой является наш контур с током) будет пропорционален току, так как пропорционально току
B
всюду под интегралом.

Заметим, что поверхность, краем которой является контур, может быть достаточно сложна, если сложен сам контур. Уже для контура в виде просто многовитковой катушки такая поверхность оказывается достаточно сложной. На практике это приводит к использованию некоторых упрощающих представлений, позволяющих легче представить такую поверхность и приближённо рассчитать поток через неё (а также в связи с этим вводятся некоторые дополнительные специальные понятия, подробно описанные в отдельном параграфе ниже). Однако здесь, при чисто теоретическом рассмотрении нет необходимости во введении каких-то дополнительных упрощающих представлений, достаточно просто заметить, что как бы ни был сложен контур, в данном параграфе мы имеем в виду «полный поток» — то есть поток через всю сложную (как бы многолистковую) поверхность, натянутую на все витки катушки (если речь идет о катушке), то есть о том, что называется потокосцеплением. Но поскольку нам здесь не надо конкретно рассчитывать его, а нужно только знать, что он пропорционален току, нам не слишком интересен конкретный вид поверхности, поток через которую нас интересует (ведь свойство пропорциональности току сохраняется для любой

Итак, мы обосновали:

Φ {\displaystyle \Phi \ }~ I,{\displaystyle \ I,}

этого достаточно, чтобы утверждать, введя обозначение L

для коэффициента пропорциональности, что
Φ=LI.{\displaystyle \Phi =LI.}
В заключение теоретического обоснования покажем, что рассуждение корректно в том смысле, что магнитный поток не зависит от конкретной формы поверхности, натянутой на контур. (Действительно, даже на самый простой контур может быть натянута — в том смысле, что контур должен быть её краем — не единственная поверхность, а разные, например, начав с двух совпадающих поверхностей, затем одну поверхность можно немного прогнуть, и она перестанет совпадать со второй). Поэтому надо показать, что магнитный поток одинаков для любых поверхностей, натянутых на один и тот же контур.

Но это действительно так: возьмём две такие поверхности. Вместе они будут составлять одну замкнутую поверхность. А мы знаем (из закона Гаусса для магнитного поля), что магнитный поток через любую замкнутую поверхность равен нулю. Это (с учетом знаков) означает, что поток через одну поверхность и другую поверхность — равны. Что доказывает корректность определения.