Одним из основных устройств в электронике и электротехнике является конденсатор. После замыкания электрической цепи начинается зарядка, после чего он сразу же становится источником тока и напряжения, в нем возникает электродвижущая сила – ЭДС. Одно из основных свойств конденсатора очень точно отражает формула емкостного сопротивления. Данное явление возникает в результате противодействия ЭДС, направленного против источника тока, используемого для зарядки. Источник тока может преодолеть емкостное сопротивление лишь путем существенных затрат его собственной энергии, которая становится энергией электрического поля конденсатора.
При разрядке устройства вся эта энергия возвращается обратно в цепь, превращаясь в энергию электрического тока. Поэтому емкостное сопротивление можно отнести к реактивному, не вызывающему безвозвратных энергетических потерь. Зарядка конденсатора происходит до того уровня напряжения, которое отдается источником питания.
Емкостное сопротивление конденсатора
Конденсаторы относятся к наиболее распространенным элементам, используемым в различных электронных схемах. Они разделяются на типы, обладающие характерными особенностями, параметрами и индивидуальными свойствами. Простейший конденсатор состоит из двух металлических пластин – электродов, разделенных слоем диэлектрика. На каждом из них имеется собственный вывод, через который осуществляется подключение к электрической цепи.
Существуют качества, присущие только конденсаторам. Например, они совершенно не пропускают через себя постоянный ток, хотя и заряжаются от него. После полной зарядки емкости, течение тока полностью прекращается, а внутреннее сопротивление устройства принимает бесконечно высокое значение.
Совершенно по-другому на конденсатор воздействует переменный ток, вполне свободно протекающий через емкость. Подобное состояние объясняется постоянными процессами зарядки-разрядки элемента. В этом случае действует не только активное сопротивление проводников, но и емкостное сопротивление самого конденсатора, возникающее как раз в результате его постоянной зарядки и разрядки.
Электрические параметры и свойства конденсаторов могут отличаться, в зависимости от различных факторов. В первую очередь они зависят от размеров и формы изделия, а также от типа диэлектрика. В разных типах устройств диэлектриком может служить бумага, воздух, пластик, стекло, слюда, керамика и другие материалы. В электролитических конденсаторах используются алюминий-электролит и тантал-электролит, что обеспечивает им повышенную емкость.
Названия других элементов определяются материалами обычных диэлектриков. Поэтому они относятся к категории бумажных, керамических, стеклянных и т.д. Каждый из них, в соответствии с характеристиками и особенностями, применяется в конкретных электронных схемах, с разными параметрами электротока.
В связи с этим, применение керамических конденсаторов необходимо в тех цепях, где требуется фильтрация высокочастотных помех. Электролитические устройства, наоборот, фильтруют помехи при низких частотах. Если же соединить параллельно оба типа конденсаторов, получится универсальный фильтр, широко применяемый во всех схемах. Несмотря на то, что их емкость является фиксированной величиной, существуют устройства с переменной емкостью, которая достигается путем регулировок за счет изменение взаимного перекрытия пластин. Типичным примером служат конденсаторы для подстройки, используемые при регулировке радиоэлектронной аппаратуры.
Свойства емкостей
Общее сопротивление
При параллельном включении нескольких конденсаторов их ёмкости складываются между собой. При этом общее ёмкостное сопротивление (согласно рассмотренным выше формулам) уменьшается. Если же все конденсаторные элементы соединены в последовательную цепочку, их суммарная ёмкость вычисляется как обратные значения каждой из составляющей.
Ёмкостное сопротивление последовательно включенных элементов в этом случае, наоборот, увеличивается. В заключение отметим, что такой характер изменения ёмкости и импеданса объясняется свойствами конденсатора, способного накапливать заряд на своих обкладках.
Емкостное сопротивление в цепи переменного тока
При включении конденсатора в цепь постоянного тока, на протяжении короткого периода времени будет наблюдаться течение по цепи зарядного тока. По окончании зарядки, когда напряжение конденсатора будет соответствовать напряжению источника тока, кратковременное течение тока в цепи прекратится. Таким образом, полностью заряженный конденсатор при постоянном токе будет своеобразным разрывом цепи или сопротивлением с бесконечно большим значением. При переменном токе конденсатор будет вести себя совершенно иначе. Его зарядка в такой цепи будет осуществляться поочередно в разных направлениях. Течение переменного тока в цепи в это время не прерывается.
Более подробное рассмотрение этого процесса указывает на нулевое значение напряжения в конденсаторе в момент его включения. После поступления к нему переменного напряжения сети начнется зарядка. В это время сетевое напряжение будет возрастать на протяжении первой четверти периода. По мере того как на обкладках накапливаются заряды, происходит увеличение напряжения самого конденсатора. После того как сетевое напряжение в конце первой четверти периода станет максимальным, зарядка прекращается и значение тока в цепи станет равным нулю.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними.
Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
- удельная ёмкость — определяет отношение величины ёмкости к массе диэлектрика;
- рабочее напряжение — номинальное значение, которое может выдержать устройство при подаче его на обкладки элемента;
- температурная стабильность — интервал, в котором ёмкость конденсатора практически не изменяется;
- сопротивление изоляции — характеризуется саморазрядом устройства и определяется током утечки;
- эквивалентное сопротивление — состоит из потерь, образуемых на выводах прибора и слое диэлектрика;
- абсорбция — процесс возникновения разности потенциалов на обкладках после разряда устройства до нуля;
- ёмкостное сопротивление — уменьшение проводимости при подаче переменного тока;
- полярность — из-за физических свойств материала, используемого при изготовлении, конденсатор сможет правильно работать, только если к обкладкам приложен потенциал с определённым знаком;
- эквивалентная индуктивность — паразитный параметр, появляющийся на контактах устройства и превращающий конденсатор в колебательный контур.
Что такое
Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.
Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.
Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами. Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.
Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.
Дополнительная информация: Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения. По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства.
Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
- Если он присоединён параллельно нагрузке, то получится фильтр, задерживающий высокие частоты. С их ростом падает сопротивление конденсатора. Соответственно, нагрузка на высоких частотах шунтируется сильнее, чем на низких.
- Если деталь подключена последовательно с нагрузкой, то получится фильтр, задерживающий низкие частоты. Эта схема также не пропускает постоянное напряжение.
- Ещё одна область применения — отделение переменной составляющей от постоянной. Например, в оконечных каскадах усилителей звуковой частоты. Чем выше ёмкость, тем более низкую частоту способен воспроизвести подключённый громкоговоритель.
В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.
Измерение сопротивления конденсаторов.
От чего зависит сопротивление конденсаторов цепей переменного тока
Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.
При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.
Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.
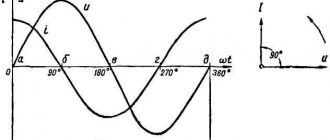
Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.
Формула емкости цилиндрического конденсатора
Теперь поговорим о том, как найти емкость конденсатора цилиндрической формы. К ним относятся конденсаторы, состоящие из двух металлических цилиндров, вставленных один в другой. Для разделения между ними расположен диэлектрик. Формула емкости конденсатора выглядит следующим образом:
Здесь видим несколько новых переменных:
- l – высота цилиндра;
- R1 и R2 – радиус первого и второго (внешнего) цилиндров;
- ln – это не переменная, а математический символ натурального логарифма. На некоторых калькуляторах он имеется.
Всегда нужно помнить, что все величины должны приводиться к единой системе, в приведенной ниже таблице указаны международные системы единиц (СИ).
Из нее видно, что все расстояния нужно приводить к метру.
Еще стоит обращать внимание на качество диэлектрика. Если толщина диэлектрика влияет только на емкость конденсатора, то его качество затрагивает сохранность энергии. Другими словами, конденсатор с качественным диэлектриком будет иметь меньший саморазряд.
Определить качество можно по числу, стоящему возле вещества, чем оно больше, тем лучше качество. Сравнение производится по вакууму, значение которого равно единице.
Как рассчитать Xc
Сила тока цепи с постоянными показателями напряжения в момент работы электроконденсатора равно 0. Ее значения в цепи с переменным напряжением после подключения конденсатора I ? 0. В итоге, цепочке с непостоянным напряжением конденсатор придает Xc меньшее, чем цепочке с неизменным показателем напряжения.
Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.
По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:
f — показатель частоты непостоянного тока, измеряется в герцах;
ω — показатель угловой частоты тока;
С — размер конденсатора в фарадах.
Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока.
Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).
Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц. Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
В чем измеряется емкостное электросопротивление
R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома. Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.
Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства. Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.
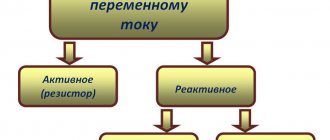
В цепях переменного тока выделяют следующие виды сопротивлений.
Активное. Активным называют сопротивление резистора. Условное обозначение
Единицей измерения сопротивления является Ом. Сопротивление резистора не зависит от частоты.
Реактивное. В разделе реактивные выделяют три вида сопротивлений: индуктивное xL и емкостное хс и собственно реактивное. Для индуктивного сопротивления выше была получена формула XL = ωL. Единицей измерения индуктивного сопротивления также является Ом. Величина xL линейно зависит от частоты.
Для емкостного сопротивления выше была получена формула XC = 1 / ωC. Единицей измерения емкостного сопротивления является Ом. Величина хс зависит от частоты по обратно-пропорциональному закону. Просто реактивным сопротивлением цепи называют величину X = XL — XC.
Полное сопротивление. Полным сопротивлением цепи называют величину
.
Из этого соотношения следует, что сопротивления Z, R и X образуют треугольник: Z – гипотенуза, R и X – катеты. Для удобства в этом треугольнике рассматривают угол φ, который определяют уравнением
и называют углом сдвига фаз. С учетом него можно дать дополнительные связи
Анализ линейных электрических цепей (стр. 3 )
Сравнение реактивного (1.22) и комплексного (1.31) сопротивлений индуктивности показывает, что на комплексной плоскости реактивное (индуктивное) сопротивление катушки откладывают на положительной вертикальной полуоси (рис. 1.32, б
), потому что эта величина мнимая и положительная.
Запишем выражения комплексных амплитуд тока и напряжения для цепи, содержащей емкость. Из (1.16) и (1.26) следует, что:
,
где UmC
и
Im
, а также j
u
и j
i
связаны соотношениями (1.27). Векторы напряжения на емкости и тока в ней сдвинуты друг относительно друга на –90°, при этом ток опережает напряжение (рис. 1.31,
в
).
Комплексное сопротивление емкости найдем как:
Здесь учтено, что .
Очевидно, что реактивное сопротивление емкости является мнимым отрицательным числом, на комплексной плоскости оно откладывается на отрицательной вертикальной полуоси (рис. 1.32, в
).
Мы уже знаем, что любое комплексное число, записанное в алгебраической форме , имеет вещественную а
и мнимую
jb
составляющие, а число, записанное в показательной форме – модуль
A
и аргумент j.
Анализ выражений (1показывает, что комплексное сопротивление резистора является вещественным и не содержит мнимой составляющей, его аргумент равен нулю; комплексное сопротивление индуктивности, наоборот, является мнимым, его аргумент равен +90°; комплексное сопротивление емкости также мнимое, но аргумент его равен –90°.
На рис. 1.33,
а
и 1.34,
а
показаны последовательные
RL
и
RC
цепи. Комплексное сопротивление последовательной
RL
цепи в алгебраической форме содержит сумму положительного вещественного резистивного сопротивления
R
и положительного мнимого индуктивного сопротивления
jXL
(рис. 1.33,
б
):
где .
В показательной форме это сопротивление запишется в виде:
,
где модуль ZRL
называется
полным сопротивлением
последовательной
RL
цепи, а аргумент j
Z
–
углом
этого сопротивления. Полное сопротивление
ZRL
и аргумент j
Z
подсчитываются, как это следует из рис. 1.33,
б
, по формулам
Пример 1.11.
Определим комплексное сопротивление цепи, изображенной на рис. 1.33,
а
, на частоте 50 Гц для
R
= 10 Ом и
L
= 100 мГн.
Рассчитаем значение индуктивного сопротивления цепи, используя (1.31),
Комплексное сопротивление RL
-цепи
Полное сопротивление
Угол сопротивления
В показательной форме комплексное сопротивление RL
-цепи
Комплексное сопротивление последовательной RC
цепи в алгебраической форме состоит из положительного вещественного резистивного сопротивления
R
и отрицательного мнимого емкостного (рис. 1.34,
б
):
где
В показательной форме это комплексное число выглядит как
,
где – полное сопротивление последовательной RC
цепи;
– угол этого сопротивления.
Комплексное сопротивление ZRC
изображено на рис. 1.34,
б
в виде вектора на комплексной плоскости. Там же показаны его проекции на вещественную и мнимую оси.
Прямоугольный треугольник, составленный из резистивного, реактивного и полного сопротивлений (рис. 1.35), называется треугольником
сопротивлений
.
Пример 1.12.
Определим комплексное сопротивление цепи, изображенной на рис. 1.34,
а
, на частоте 5 кГц для
R
= 100 Ом,
С
= 318 нФ.
Рассчитаем значение емкостного сопротивления цепи
Комплексное сопротивление RC
-цепи
Вектор комплексного сопротивления RC
-цепи изображен на рис. 1.36.
Запишем комплексное сопротивление последовательной RLC
цепи (рис. 1.37,
а
). Оно будет содержать положительное вещественное резистивное сопротивление
R
и мнимое сопротивление , знак которого будет зависеть от соотношения индуктивного
XL
и емкостного
XC
сопротивлений, следовательно:
,
где .
Напомним, что значения XL
и
XC
зависят от частоты и от соответствующих элементов
L
и
С
, поэтому может случиться так, что на определенной частоте и при определенных значениях
L
и
С
значение
XL
будет больше значения
XC
, как это показано на рис. 1.37,
б
, или наоборот, значение
XC
будет больше, чем
XL
(рис. 1.37,
в
).
Из треугольника сопротивлений легко вычислить резистивное и реактивное сопротивления, зная полное сопротивление и его угол:
.
Случай, когда реактивное сопротивление Х =
0, т. е.
XL
=
XC
, является особым. Когда это имеет место, то говорят, что в последовательной
RLC
цепи возникает
резонанс напряжений
. Частота, на которой индуктивное и емкостное сопротивления оказываются равными, называется
частотойрезонансанапряжений
. Комплексное сопротивление всей
RLC
цепи равно при этом резистивному сопротивлению
R
. В дальнейшем явление резонанса напряжений будет рассмотрено более детально.
Пример 1.13.
Определим резистивное и реактивное сопротивления последовательной
RLC
цепи, комплексное сопротивление которой
Резистивное сопротивление
Реактивное сопротивление
Сопротивление X
=
XL
–
XC
положительное, т. е.
XL
>
XC
, треугольник сопротивлений такой цепи изображен на рис. 1.38.
При параллельном соединении элементов удобнее иметь дело не с сопротивлениями, а с проводимостями – резистивной G =
1/
R
, реактивными и , полной
Y =
1/
Z
и комплексной
Y =
1/
Z
. Если при последовательном соединении элементов складыва
лись их комплексные сопротивления, то при параллельном соединении складываются их проводимости.
Для параллельной RLC
цепи (рис. 1.39,
а
) ее комплексная проводимость запишется в виде:
,
где G =
1/
R
– резистивная проводимость;
– емкостная проводимость;
– индуктивная проводимость;
– реактивная проводимость;
– полная проводимость;
– угол проводимости.
Резистивную и реактивную проводимости можно найти из треугольника проводимостей (рис. 1.39, б
):
.
Случай, когда реактивная проводимость В
равна нулю, т. е. когда также представляет особый интерес. В этот момент в параллельной
RLC
цепи наступает
резонанс токов
. Поэтому частота, на которой происходит совпадение реактивных проводимостей ветвей получила название
частоты резонанса токов
. Комплексная проводимость всей цепи при резонансе становится равной резистивной проводимости
G
. Более подробно явление резонанса токов будет рассмотрено позднее.
Пример 1.14.
Определить комплексное сопротивление параллельной
RLC
цепи (рис. 1.39,
а
) на частоте
f
= 1 кГц для
R
= 100 Ом,
L
= 10 мГн,
С
= 10 мкФ.
Элементы цепи соединены параллельно, поэтому рассчитаем вначале комплексную проводимость YRLC
, используя выражение (1.36).
Резистивная проводимость
Индуктивная проводимость
Емкостная проводимость
Комплексная проводимость цепи
Комплексное сопротивление цепи обратно пропорционально комплексной проводимости, поэтому
Из данного раздела мы узнали, что:
1.3. Расчет реакций цепи в символической форме
Расчет реакций в цепи с одним источником
. Используется следующий порядок расчета:
1. Цепь, содержащую источник гармонических колебаний, преобразуют, заменяя ее элементы их комплексными сопротивлениями, а мгновенные значения эдс, токов и напряжений записывая в комплексной (символической) форме.
2. Рассчитывают комплексные значения токов в ветвях и напряжений на сопротивлениях, используя закон Ома и законы Кирхгофа.
3. Определяют соответствующие мгновенные значения токов и напряжений в цепи.
Пример 1.15.
Определим мгновенные значения тока и напряжений на элементах цепи, содержащей источник гармонического напряжения В, сопротивление
R
= 300 Ом, индуктивность
L
= 0,6 Гн и емкость
С
= = 0,625 мкФ (рис. 1.40).
В соответствии с порядком расчета реакции в цепи с одним источником заменяем элементы цепи их комплексными сопротивлениями.
Анализируя выражение для мгновенного значения напряжения u
(
t
), определяем, что круговая частота w = 2000 рад/с, т. е. частота колебаний
f
= w/(2p) = = 318,3 Гц. Сопротивление
R
= 300 Ом остается неизменным. Индуктивность
L
= 0,6 Гн заменяется сопротивлением
Емкость С
= 0,625 мкФ заменяется сопротивлением
Гармоническое напряжение представим в показательной форме записи в виде
Ток i
(
t
) заменяется на комплексный ток
Im
, а напряжения
uR
(
t
),
uL
(
t
) и
uC
(
t
) заменяются комплексными напряжениями
UmR
,
UmL
и
UmС
соответственно.
В результате получаем схему, изображенную на рис. 1.41.
Для определения тока и напряжений в этой схеме рассчитаем вначале комплексное сопротивление цепи Z
относительно зажимов источника. Все сопротивления включены последовательно, поэтому
Отметим, что индуктивное и емкостное сопротивления цепи частично компенсировали друг друга и что реактивное сопротивление цепи меньше по величине, чем сопротивление любого из реактивных элементов.
Фактически возможно полностью исключить наличие реактивного сопротивления в цепи, изменив частоту генератора напряжения до выполнения условия |ZL
| = |
ZC
|.
В рассматриваемом примере сопротивление цепи имеет индуктивный характер, поскольку реактивная составляющая комплексного сопротивления цепи имеет знак «плюс».
Комплексный ток Im
в цепи определим, используя закон Ома для комплексного напряжения
Um
источника и комплексного сопротивления
Z
. Имеем:
Преобразуя комплексное сопротивление Z
в показательную форму для упрощения деления комплексных чисел, получаем
Амплитудное значение тока равно 0,02 А, а начальная фаза равна –53°.
Напряжения на сопротивлениях цепи определяем, умножая ток Im
на соответствующие сопротивления.
Ток Im
имеет начальную фазу (–53°), напряжение
UmR
имеет такую же начальную фазу, т. е. векторы
Im
и
UmR
направлены по одной прямой на векторной диаграмме, изображенной на рис. 1.42.
Напряжение на индуктивности опережает ток на 90°, таким образом, UmL
опережает вектор на горизонтальной оси рис. 1.42 на 37°.
Напряжение на емкости отстает от тока на 90°, а от горизонтальной оси на 143°.
Отметим также, что сдвиг фаз между UmL
и
UmС
составляет 180°.
В соответствии с законом напряжений Кирхгофа
Последние два слагаемых представляют собой сумму напряжений на индуктивности и емкости, и этот суммарный вектор может быть направлен либо по UmL
, либо по
UmС
в зависимости от того, какое из этих напряжений больше по величине. В нашем случае он имеет направление
UmL
.
Вектор UmR
может быть добавлен к сумме
UmL
+
UmС
и результатом является вектор
Um
, как показано на рис. 1.42.
Мгновенные значения тока и напряжений на элементах цепи можно записать в виде
Векторная диаграмма часто бывает полезна при объяснении и интерпретации результатов расчета.
Пример 1.16.
Найдем токи и напряжения в цепи, изображенной на рис. 1.43, если заданы значения
R
1 = 2 Ом,
R
2 = 2 Ом, Х
L
= 4 Ом, Х
С
= 2 Ом, .
Во-первых, определим комплексное сопротивление Z
аб параллельного соединения резистора
R
2 и емкостного сопротивления Х
С
:
Сопротивление Z
аб можно представить в виде
Z
аб = =
R
аб –
jX
аб.
Получаем эквивалентную схему, изображенную на рис. 1.44.
Эквивалентное комплексное сопротивление цепи определяется как
Ток (рис. 1.45) определяется по закону Ома:
Токи Im
1 и
Im
2 определяем по формулам разброса:
Следует отметить, что согласно закону токов Кирхгофа, Im
1 +
Im
2 =
Im
. Векторная диаграмма токов приведена на рис. 1.46.
Определим напряжения на элементах цепи (рис. 1.43):
Согласно закону напряжений Кирхгофа (рис. 1.47)
Расчет реакций в цепи с несколькими источниками.
Все методы расчета цепей в режиме постоянного тока применимы и к расчету цепей при гармоническом воздействии. Методы наложения, узловых напряжений, контурных токов, эквивалентного генератора используются для определения реакций в цепи с несколькими источниками гармонических колебаний.
Расчет выполняется для символической формы записи токов, напряжений и сопротивлений цепи.
Пример 1.17.
Методом наложения определим токи в ветвях цепи, изображенной на рис. 1.48, если заданы значения
R
1 = 2 Ом,
ХL
= 4 Ом,
ХС
= 2 Ом,
Выберем направления токов в ветвях цепи (рис. 1.48). Поскольку в схеме два источника, то истинные направления токов неизвестны, поэтому выбираем их произвольно.
Метод наложения основан на принципе суперпозиции, согласно которому реакция линейной цепи на сумму воздействий равна алгебраической сумме реакций от каждого воздействия в отдельности.
Частичные схемы, в каждой из которых оставлен только один источник, а другой заменен его внутренним сопротивлением, изображены на рис. 1.49, а
и 1.49,
б
.
Рассчитаем токи в первой частичной схеме (рис. 1.49, а
). Внутреннее сопротивление источника тока равно бесконечности, поэтому . По закону Ома
Рассмотрим вторую частичную схему (рис. 1.49, б
). Ток равен току источника тока, т. е.
Токи и рассчитываем, используя формулу разброса,
Токи в ветвях исходной схемы
Пример 1.18.
Методом узловых напряжений определим токи в ветвях цепи, изображенной на рис. 1.48.
Заземляем узел 2. Потенциал этого узла равен нулю, Vm
2 = 0.
Для узла 1 составляем уравнение состояния:
В этом уравнении Y
11 – это собственная проводимость 1 узла, т. е. сумма проводимостей всех ветвей, подсоединенных к узлу 1:
Y
12 – взаимная проводимость узлов 1 и 2, совпадающая в рассматриваемом примере с величиной
Y
11;
Im
у1 – узловой ток узла 1:
Из уравнения состояния находим потенциал первого узла
Токи в ветвях находим по закону Ома:
Значения токов в ветвях цепи рис. 1.48 те же самые, что и при расчете методом наложения.
Пример 1.19.
Методом контурных токов определим токи в ветвях цепи, изображенной на рис. 1.48.
Выберем направления обхода контуров в цепи (рис. 1.50).
Контурный ток
Для определения контурного тока составляем уравнение состояния:
В этом уравнении Z
11 – собственное сопротивление 1 контура, равное сумме сопротивлений всех ветвей, образующих этот контур:
Z
12 – взаимное сопротивление 1 и 2 контуров:
Um
к1 – контурное напряжение:
Из уравнения состояния находим контурный ток Im
к1:
Зная контурные токи, находим токи ветвей,
Значения токов совпадают с теми, которые были получены при расчете цепи методами наложения и узловых напряжений.
Пример 1.20.
Методом эквивалентного генератора определим ток
Im
1 в цепи, изображенной на рис. 1.48.
Разомкнем ветвь с емкостью и для определения напряжения холостого хода Um
хх составим уравнение по второму закону Кирхгофа
В режиме холостого хода ток Im
хх = –
Im
г, поэтому
Сопротивление эквивалентного генератора Z
эг равно
Ток Im
1 найдем по формуле
Получаем то же самое значение Im
1, что и при применении других методов расчета.
Из данного раздела мы узнали, что
1.4. Комплексный коэффициент передачи
Рассмотрим электрическую цепь, изображенную на рис. 1.51.
Нас может интересовать любая реакция цепи (напряжение или ток в любом элементе или ветви цепи) на любое из приложенных воздействий. В этом случае цепь удобно представить четырехполюсником, на входе которого включен источник с заданным воздействием, а на выходе – интересующий нас элемент, например, как это сделано на рис. 1.52.
Символическое изображение напряжений и токов на входе и выходе четырехполюсника, показано на рис. 1.53.
Важнейшей характеристикой линейной электрической цепи является комплексный коэффициент передачи Н
. Он определяется отношением комплексной амплитуды реакции к комплексной амплитуде воздействия.
В зависимости от того, что считается реакцией и воздействием, различают следующие виды коэффициентов передачи.
1. Комплексный коэффициент передачи по напряжению
2. Комплексный коэффициент передачи по току
3. Комплексное передаточное сопротивление
4. Комплексная передаточная проводимость
Комплексное число H
может быть представлено в показательной форме
где Н
– модуль передаточной функции, а j – ее аргумент.
Действительно, рассмотрим передаточную функцию
.
Модуль передаточной функции
представляет собой отношение амплитуды гармонической реакции цепи к амплитуде гармонического воздействия, т. е. показывает во сколько раз амплитуда гармонического колебания на входе цепи изменилась при прохождении колебания через цепь. Поэтому величину Hu
называют
коэффициентом передачи по напряжению
.
Аргумент передаточной функции
показывает изменение начальной фазы входного колебания после передачи этого колебания по цепи и называется фазовым сдвигом
.
Знание комплексного коэффициента передачи цепи позволяет вычислить реакцию цепи на гармоническое воздействие. Амплитуда реакции равна
а начальная ее фаза
Другими словами, чтобы найти амплитуду гармонического колебания на выходе цепи, нужно амплитуду входного гармонического колебания умножить на коэффициент передачи по напряжению, а чтобы найти начальную фазу выходного гармонического колебания, нужно к начальной фазе входного гармонического колебания добавить фазовый сдвиг, вносимый цепью.
В символической форме записи комплексная амплитуда гармонического колебания на выходе цепи определяется из соотношения:
Аналогичным образом вычисляют коэффициент передачи по току
и сдвиг фаз колебания тока
полное передаточное сопротивление цепи
и фазовый угол этого сопротивления
а также полную передаточную проводимость
и ее фазовый угол
В общем виде можно записать
Очевидно, что в схеме рис. 1.51 в качестве реакции может выступать напряжение или ток в любом элементе или любой ветви цепи, а в качестве воздействия использоваться не только напряжения или токи источников, но и любые напряжения или токи элементов (ветвей) цепи.
Пример 1.21.
Найдем комплексный коэффициент передачи по напряжению цепи, приведенной в Примере 1.15, если реакцией цепи является напряжение на емкости
uC
(
t
).
При решении Примера 1.15 воздействие было записано в символической форме
Напряжение на емкости, т. е. реакция цепи, также было определено:
Комплексный коэффициент передачи
Коэффициент передачи по напряжению
показывает, что при прохождении по цепи амплитуда воздействия уменьшилась в 10 раз.
Сдвиг фаз
показывает, что напряжение на емкости отстает от входного колебания на 143°.
Пример 1.22.
Найдем комплексный коэффициент передачи по току цепи, изображенной на рис. 1.54, если
Im
г = 5
ej
90°, А,
R
2 = 10 Ом,
L
= 30 мГн,
f
= 50 Гц, реакцией цепи является ток в индуктивности.
Для расчета комплексного коэффициента передачи по току
необходимо определить ток в индуктивности. Используя формулу разброса, получаем:
Комплексный коэффициент передачи по току
Очевидно, что комплексный коэффициент передачи цепи определяется значениями элементов цепи R
2,
L
и частоты
f
.
Пример 1.23.
Найдем напряжение на индуктивности
uL
(
t
) в цепи, приведенной в Примере 1.22, если комплексное передаточное сопротивление
HZ
= 6,86
ej
46,8° Ом.
Амплитуда напряжения на индуктивности
Начальная фаза напряжения на индуктивности
Мгновенное значение напряжения
Из данного раздела мы узнали, что
Вопросы и задания для самоконтроля
1. Какие колебания называются гармоническими?
2. Какие параметры характеризуют гармоническое колебание?
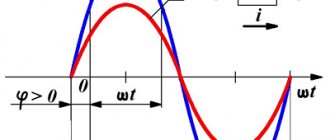
3. Как определяется величина и знак начальной фазы гармонического колебания по его графику?
4. Как связаны частота и период гармонического колебания?
5. Записать выражение для мгновенного значения тока, график которого изображен на рис. 1.5, б
, если период колебания
Т
= 2 с. Определить значение тока в момент времени
t
1 =
T
/8.
6. Построить в одной системе координат графики напряжений u
1(
t
) = ,
u
2(
t
) = .
7. Какая связь между векторным и временным представлением гармонических колебаний?
8. Построить векторы гармонических колебаний, приведенных в п. 6.
9. Построить в одной системе координат графики гармонических колебаний, которым соответствуют векторы и , вращающиеся с одинаковой частотой. Определить сдвиг фаз этих колебаний.
10. Какая связь между параметрами комплексного и временного представления гармонических колебаний?
11. Сформулировать закон Ома для резистивной, индуктивной и емкостной цепей.
12. Какой сдвиг фаз между напряжением и током в резисторе (емкости, индуктивности)?
13. Как рассчитывается комплексное сопротивление последовательного соединения R
,
L
,
C
элементов?
14. Как рассчитывается комплексная проводимость параллельного соединения R
,
L
,
C
элементов?
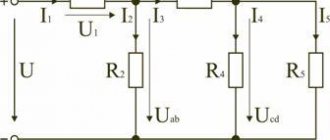
15. Определить комплексное сопротивление цепи, изображенной на рис. 1.55, если
R
1 = 20 Ом,
R
2 = 40 Ом,
ХL
= 30 Ом,
ХС
= 40 Ом.
Построить треугольник сопротивления цепи.
16. Какие методы используются для расчета цепей с источниками гармонических колебаний?
17. Рассчитать токи в ветвях цепи, изображенной на рис. 1.55, если на вход подается напряжение , В. Построить векторную диаграмму токов.
18. Рассчитать ток Im
2 в цепи, изображенной на рис. 1.56, методом наложения и методом эквивалентного генератора, если заданы сопротивления
R
= 10 Ом,
ХL
= 30 Ом,
ХС
= 20 Ом и
Um
= 10
ej
0° В,
Im
г =
ej
270° А.
19. Что такое комплексный коэффициент передачи? Какие виды комплексных коэффициентов передачи известны?
20. Определить коэффициенты передачи в цепи Примера 1.16, если реакцией является Im
2.
* Следует различать резисторы, катушки индуктивности и конденсаторы как физические элементы электрической цепи и резистивные, индуктивные и емкостные элементы как идеализированные элементы, обладающие свойствами необратимого рассеяния энергии или свойствами накопления энергии магнитного и электрического полей. В инженерной практике резистивный, индуктивный и емкостной элементы часто называют просто сопротивлением, индуктивностью и емкостью, отождествляя по существу элемент с его параметром. В дальнейшем для простоты, где это не приведет к недоразумению, мы также будем пользоваться этой терминологией.
| Из за большого объема этот материал размещен на нескольких страницах: 3 |
Получить текст
Элемент r (резистор)
Зададим напряжение и ток в виде соотношений
Известно, что для резистора ψu = ψi, тогда для р получим
Из уравнения (2.32) видно, что мгновенная мощность всегда больше нуля и изменяется во времени. В таких случаях принять рассматривать среднюю за период Т мощность
.
Если записать Um и Im через действующие значения U и I: ,, то получим
По форме уравнение (2.34) совпадает с мощностью на постоянном токе. Величину Р равную произведению действующих значений тока и напряжения называют активной мощностью. Единицей ее измерения является Ватт (Вт).
Способы соединения элементов
Монтаж изделия на плату может быть вертикальным или горизонтальным. При использовании нескольких изделий они могут быть соединены между собой разными способами.
Параллельное соединение
Для его организации нужно подключить группу деталей к электроцепи так, чтобы обкладки всех деталей были подсоединены напрямую к местам включения. Поскольку все компоненты получают заряд от одного источника тока, у них будет одинаковая разность потенциалов. Но так как заряд копится на каждом изделии отдельно, количество электричества на группе можно выразить как сумму количеств на ее деталях.
Это справедливо и для емкостных данных – значение для конфигурации равно сумме значений каждой единицы. Поэтому такую группу можно считать равной одному конденсатору, емкостной параметр которого равен сумме таковых для всех частей.
Последовательное соединение
Эта схема подразумевает соединение устройств одно за другим, когда к местам подключения к цепи подсоединены только два крайних изделия. Количество электричества для каждой детали будет одинаковым. При этом, чем менее емкое устройство, тем большее значение напряжения на нем будет наблюдаться.
Важно! Емкостной показатель такой системы будет еще меньше, чем у устройства, обладающего наименьшим его значением. Соотношение выглядит так: 1/С = 1/С1 + 1/С2 + 1/С3 + … Опираясь на него, можно произвести вывод непосредственно формулы С. Для двух элементов: С = С1*С2 / С1+С2.
Последовательное подключение
Смешанное соединение
Такая сложная конструкция содержит фрагменты с двумя вышеприведенными типами соединений. Чтобы подсчитать полную емкость, схему делят на простые блоки, состоящие только из деталей, соединенных каким-то одним образом. Находят эквивалентные значения для каждого блока и затем рисуют схему заново в упрощенном виде. Рассчитывают данные для получившейся системы.
Чтобы суметь подобрать подходящий конденсаторный набор, нужно уметь узнавать емкостные данные. Важно также знать, как рассчитывается показатель для конфигурации из нескольких деталей, соединенных между собой тем или иным образом.
Элемент l (индуктивность)
Известно, что в индуктивности соотношение фаз ψu = ψi + 90°. Для мгновенной мощности имеет
.
Усредняя уравнение (2.35) по времени за период Т получим
.
Для количественной оценки мощности в индуктивности используют величину QL равную максимальному значению рL
и называют ее реактивной (индуктивной) мощностью. Единицей ее измерения выбрали ВАр (вольт-ампер реактивный). Уравнение (2.36) можно записать через действующие значения U и I и используя формулу UL = I XL получим
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.