Всем доброго времени суток. В прошлой статье я начал рассказывать о магнитном поле в веществе и затронул вопросы напряженности магнитного поля, магнитной проницаемости и восприимчивости, а также рассказал о намагничивании и гистерезисе в ферромагнетиках. Однако магнитное поле зависит не только от свойств веществ, но и от их формы. Об этом я и расскажу в статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Что такое магнитная цепь?
Магнитной цепью называется, соединение магнетиков, по которым замыкается магнитный поток. То есть сердечник, на который намотан любой дроссель, трансформатор, катушка индуктивности и т.д. является магнитной цепью. Более того если веществом такого сердечника является воздух (то есть катушки индуктивности не имеющие каркаса), то и он является магнитной цепью. Очень часто магнитную цепь называют магнитопроводом, что по сути так и есть, сердечник проводит магнитное поле, также как и проводник проводит электрический ток. Более того на магнитные цепи распространяются законы электрического тока: закон Ома, правила Кирхгофа и так далее, но об этом ниже.
Магнитные цепи бывают однородные и неоднородные. Однородными называют магнитные цепи, которые на протяжении всей своей длины изготовлены из одного материала (то есть имеет одинаковую магнитную проницаемость) и одинаковое поперечное сечение. Если хотя бы одно из этих условий не выполняется, то такая магнитная цепь называется неоднородной.
Также различают разветвлённые и неразветвлённые магнитные цепи. То есть не разветвлённые цепи состоят из одного контура, а разветвлённые, соответственно, состоят из нескольких контуров, по которым замыкается магнитный поток. Разветвлённые цепи могут быть симметричные и несимметричные. У симметричных цепей магнитный поток каждого контура одинаков.
Постоянные магниты
В измерительных приборах, электрической аппаратуре и других устройствах в качестве источников намагничивающей силы широко применяют постоянные магниты.
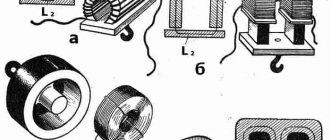
На рис. 9.12 схематично изображены магнитные системы магнито-электрического измерительного прибора (а) и поляризованного реле (б). Эти системы, как и большинство им подобных, имеют несколько участков: 1) из магнитно-твердого материала— постоянного магнита 1; 2) из магнитно-мягкого материала 2, служащего магнитопроводом, и воздушного зазора 3, форма и размеры которого определяются конструкцией и назначением устройства. При расчете магнитной цепи с постоянным магнитом требуется определить магнитный поток и индукцию в воздушном зазоре или по заданному потоку найти оптимальные размеры постоянного магнита (наименьшие объем и габариты).
Характеристики размагничивания постоянных магнитов
Величины остаточной магнитной индукции Вг и коэрцитивной силы Hс характеризуют материал постоянного магнита: чем они больше, тем выше его качество. Как известно, на петле гистерезиса Вг соответствует Н = 0, а при В = 0 Н = Нс. Рис. 9.12. Магнитные цепи с постоянными магнитами
Рис. 9.13. Характеристики размагничивания постоянных магнитов: 1 — АНКО-4; 2 — АНКО-2; З-АН-2; 4 — сталь с 30% СО
Промежуточные магнитные состояния определяются частью петли магнитного гистерезиса, лежащей во второй четверти, — характеристикой размагничивания (рис. 9.12). Эта характеристика используется при расчете постоянных магнитов. Согласно закону полного тока, сумма магнитных напряжений участков магнитной цепи (рис. 9.12) равна нулю, так как внешняя намагничивающая сила (ампер-витки) отсутствует: где Uм.т — магнитное напряжение постоянного магнита; — сумма магнитных напряжений всех участков магнитной цепи, включая воздушные зазоры, но без постоянного магнита.
Левая и правая части равенства (9.5) связаны с магнитной индукцией и потоком определенными зависимостями: Фт(Uм.т) — кривая размагничивания постоянного магнита (по форме повторяет кривую размагничивания материала, из которого выполнен постоянный магнит); Фм(Uм.с) — кривая намагничивания части конструкции устройства, изготовленной из магнитно-мягкого материала; Ф0(Uм0) — прямая, проходящая через начало координат и повторяющая в других масштабах зависимость
Параметры магнитных цепей
Как я уже говорил многие законы для электрических цепей подходят и для магнитных. Для обобщения этих законов необходимо ввести некоторые параметры, характеризующие магнитные цепи. Представим неоднородную и неразветвлённую магнитную цепь
Неоднородная и неразветвлённая магнитная цепь.
Данная цепь состоит из трёх участков длиной l1, l2, l3, имеющих поперечное сечение S1, S2, S3, причем магнитное поле создается током I, протекающим по соленоиду, содержащему N витков. Так как линии магнитного поля в основном замыкаются через магнитопровод, то магнитный поток Φ, можно считать одинаковым на всём протяжении магнитной цепи и определяется следующим выражением
где В – магнитная индукция,
S – площадь поперечного сечения, которую пронизывает магнитный поток.
Таким образом, магнитный поток является аналогом силы тока в электрических цепях.
Согласно закона полного тока и циркуляции вектора магнитной индукции составим уравнение
где В1, В2, В3 – соответственно магнитная индукция на участках l1, l2, l3 магнитной цепи;
μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м;
μ1, μ2, μ3 – соответственно относительная магнитная проницаемость участков l1, l2, l3 сердечника;
N – количество витков провода;
I – ток, протекающий по проводу.
При использовании ферромагнетиков определение относительной магнитной проницаемость составляет некоторые трудности, поэтому вместо магнитной индукции в данном законе используют напряженность магнитного поля, следовательно для данной магнитной цепи закон полного тока можно представить следующим образом
Выражая магнитную индукцию через магнитный поток, получим следующее выражение
где S1, S2, S3 – соответственно, площадь поперечного сечения участков l1, l2, l3 магнитной цепи.
Таким образом, проводя аналогию с электрической цепью, получим следующие параметры магнитной цепи
где Em – магнитодвижущая сила,
Rm – магнитное сопротивление цепи.
Следовательно, вышеописанное выражение можно представить следующим выражением
где Rm1, Rm1, Rm1 – соответственно магнитные сопротивления участков l1, l2, l3 магнитной цепи.
9.1.3. Свойства ферромагнитных материалов
Магнитное состояние любой точки изотропной среды, т. е. среды с одинаковыми свойствами во всех направлениях, вполне определяется вектором напряженности магнитного поля Н
и вектором магнитной индукции
В
, которые совпадают друг с другом по направлению.
Основная единица магнитной индукции в системе СИ называется тесла (Тл): 1 Тл = 1 Вб/м2 = 1 В·с/м2. Это индукция такого однородного магнитного поля, в котором магнитный поток Ф
через поверхность площадью 1 м2, перпендикулярную направлению магнитных линий поля, равен одному веберу (Вб).
В вакууме индукция и напряженность магнитного поля связаны простым соотношением: В = m0Н, где m 0 = 4p·10-7 Гн/м — магнитная постоянная. Для ферромагнитных материалов зависимость индукции от напряженности магнитного поля В(H)
в общем случае нелинейная.
Для того чтобы экспериментально исследовать магнитные свойства ферромагнитного материала, необходимо все измерения производить на образце, в котором магнитное поле однородное. Таким образцом может быть тороид, изготовленный из исследуемого ферромагнитного материала (рис. 9.5), длина магнитных линий в котором много больше его поперечных размеров (тонкостенный тороид). На тороиде находится равномерно навитая обмотка с числом витков w
.
Можно считать, что в тороиде из ферромагнитного изотропного материала с плотно намотанными витками все магнитные линии — окружности, а векторы напряженности и индукции магнитного поля направлены по касательной к соответствующей окружности. Так, на рис. 9.5 показаны средняя магнитная линия и векторы Н
и
В
в одной из ее точек.
При расчете напряженности и индукции магнитного поля в тонкостенном тороиде можно считать, что все магнитные линии имеют одинаковую длину, равную длине средней линии 2p
r
.
Предположим, что ферромагнитный материал тонкостенного тороида полностью размагничен и тока I
в обмотке нет (
В
= 0 и
Н
= 0). Если теперь плавно увеличивать постоянный ток
I
в обмотке катушки, то в ферромагнитном материале возникнет магнитное поле, напряженность которого определяется законом полного тока (9.1):
H
=Iw/2pr.
(9.3)
Каждому значению напряженности H
магнитного поля в тонкостенном тороиде соответствует определенная намагниченность ферромагнитного материала, а следовательно, и соответствующее значение магнитной индукции
В
.
Если начальное магнитное состояние материала тонкостенного тороида характеризуется значениями Н
= 0,
В
= 0, то при плавном нарастании тока получим нелинейную зависимость
В(Н),
которая называется кривой первоначального намагничивания (рис. 9.5, штриховая линия). Начиная с некоторых значений напряженности
H
магнитного поля индукция
В
в тонкостенном ферромагнитном тороиде практически перестает увеличиваться и остается равной
Вmax
. Эта область зависимости
В(Н)
называется областью технического насыщения.
Если, достигнув насыщения, начать плавно уменьшать постоянный ток в обмотке, т. е. уменьшать напряженность поля (9.3), то индукция также начнет уменьшаться. Однако зависимость В(Н)
уже не совпадает с кривой первоначального намагничивания. Изменив направление тока в обмотке и увеличив его значение, получим новый участок зависимости
В(Н).
При значительных отрицательных значениях напряженности магнитного поля снова наступит техническое насыщение ферромагнитного материала. Если теперь продолжить эксперимент: сначала уменьшать ток обратного направления, затем увеличивать ток прямого направления до насыщения и т. д., то после нескольких циклов перемагничивания для зависимости
В(Н)
будет получена симметричная кривая (рис. 9.5, сплошная линия). Этот замкнутый цикл
В(Н)
называется предельной статической петлей гистерезиса (или предельным статическим циклом гистерезиса) ферромагнитного материала. Если во время симметричного перемагничивания область технического насыщения не достигается, то симметричная кривая
В(Н)
называется симметричной частной петлей гистерезиса ферромагнитного материала.
Предельный статистический цикл гистерезиса ферромагнитных материалов характеризуется следующими параметрами:
Нс
— коэрцитивной силой,
Вr
— остаточной индукцией и
k=Br/BH—l0Hc
— коэффициентом прямоугольности.
По значению параметра Hс
предельного статического цикла гистерезиса ферромагнитные материалы делятся на группы:
1) магнитные материалы с малыми значениями коэрцитивной силы (Hс
<� 0,05…0,01 А/м) называются магнитно-мягкими;
2) магнитные материалы с большими значениями коэрцитивной силы (Hс
> 20…30 кА/м) называются магнитно-твердыми.
Магнитно-твердые материалы используются для изготовления постоянных магнитов, а магнитно-мягкие — для изготовления магнитопроводов электротехнических устройств, работающих в режиме перемагничивания по предельному или частым циклам.
Магнитно-мягкие материалы в свою очередь делятся на три типа: магнитные материалы с прямоугольной предельной статической петлей гистерезиса, у которых коэффициент прямоугольности k
> 0,95 (рис. 9.6, а); магнитные материалы с округлой предельной статической петлей гистерезиса, у которых коэффициент прямоугольности 0,4 < <
k
< 0,7 (рис. 9.6, б); магнитные материалы с линейными свойствами, у которых зависимость
В(H)
практически линейная:
В =mrm0Н
(рис. 9.6, в), где
mr
— относительная магнитная проницаемость.
Все типы магнитных характеристик ферромагнитных материалов могут быть получены на образцах, изготовленных либо из различных ферромагнитных сплавов, либо из ферромагнитной керамики (ферриты). Ценное свойство ферритов в отличие от ферромагнитных сплавов — их высокое удельное электрическое сопротивление.
Магнитопроводы из ферромагнитных материалов с прямоугольным предельным статическим циклом гистерезиса применяются в оперативной памяти цифровых ЭВМ, магнитных усилителях и других устройствах автоматики. Ферромагнитные материалы с округлым предельным статическим циклом гистерезиса используются при изготовлении магнитопроводов электрических машин и аппаратов. Магнитопроводы этих устройств обычно работают в режиме перемагничивания по симметричным частным циклам. При основных расчетах магнитопроводов таких электротехнических устройств симметричные частные циклы заменяют основной кривой намагничивания ферромагнитного материала, которая представляет собой геометрическое место вершин симметричных частных циклов тонкостенного ферромагнитного тороида (рис. 9.7), полученных при синусоидальном токе низкой частоты в обмотке.
По основной кривой намагничивания ферромагнитного материала определяют зависимость абсолютной магнитной проницаемости
ma
=
mrm0
=
В/Н
(9.4)
от напряженности Н
магнитного поля, которая показана на рис. 9.7 штриховой линией.
На рис. 9.8 приведены основные кривые намагничивания некоторых электротехнических сталей, используемых в электрических машинах, трансформаторах и других устройствах, а также чугуна и пермаллоя.
Из ферромагнитных материалов с линейными свойствами изготовляют участки магнитопроводов для катушек индуктивности колебательных контуров с высокой добротностью. Такие контуры применяются в различных радиотехнических устройствах (приемниках, передатчиках), в малогабаритных антеннах средств связи и т. д.
Если на участке магнитопровода с площадью поперечного сечения S
магнитное поле неоднородное, то часто расчет можно вести, пользуясь средним значением индукции
Вср = Ф/S
и напряженностью
Нср
на средней магнитной линии. Например, для тороида с прямоугольной формой поперечного сечения, внутренним радиусом
rt,
внешним радиусом
r2
и высотой
h
, изготовленного из магнитного материала с линейными свойствами
В = mrm0H
при
mr
= const (рис. 9.6, в),
где
Из полученных выражений следует, что
В дальнейшем для упрощения расчетов неоднородность магнитного поля в поперечном сечении каждого участка магнитопровода учитывать не будем, и будем считать, что поле в каждом участке однородное и определяется значениями напряженности и индукции на средней магнитной линии.
Законы магнитной цепи
Как я писал выше многие законы электрических цепей подходят и для магнитных цепей. Например, закон Ома для магнитной цепи звучит следующим образом: магнитный поток Φ прямо пропорционален магнитодвижущей силе Em и обратно пропорционален полному сопротивлению магнитной цепи Rm. И выражается он следующей формулой, называемой также формулой Гопкинсона
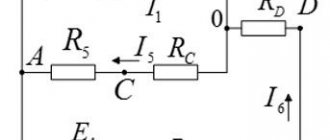
Кроме закона Ома для магнитных цепей действуют правила Кирхгофа. Так первый закон Киргхофа для магнитных цепей звучит следующим образом: алгебраическая сумма магнитных потоков ∑Φ в узле магнитной цепи равна нулю. Для пояснения данного правила изобразим разветвлённую магнитную цепь
Разветвлённая магнитная цепь.
Данная магнитная цепь состоит из двух контуров АБВГ и АГДЕ. Ветвь АГ создает магнитный поток Φ2, который в точке А делится на два потока Φ1 и Φ3. Таким образом, в точке А алгебраическая сумма магнитных потоков равна нулю
Аналогично второй закон Кирхгофа для магнитной цепи звучит следующим образом: в контуре магнитной цепи алгебраическая сумма магнитодвижущижся сил ∑Еm равна алгебраической сумме магнитных напряжений на отдельных участках.
Магнитное напряжение на участке цепи определяется произведение магнитного потока Φ на магнитное сопротивление участка Rm, следовательно, второй закон Кирхгофа будет иметь вид
тогда для магнитной цепи изображённой выше второе правило Кирхгофа будет иметь вид
Использую данные соотношения достаточно просто рассчитать необходимые геометрические размеры магнитопроводов для различных магнитных систем, например, трансформаторы, дроссели, катушки индуктивности и так далее, чем мы и займёмся ниже.
Указанная в предыдущей лекции формальная аналогия между электрическими и магнитными цепями позволяет распространить все методы и технику расчета нелинейных резистивных цепей постоянного тока на нелинейные магнитные цепи. При этом для наглядности можно составить эквивалентную электрическую схему замещения
исходной магнитной цепи, с использованием которой выполняется расчет.
Нелинейность магнитных цепей определяется нелинейным характером зависимости , являющейся аналогом ВАХ и определяемой характеристикой ферромагнитного материала . При расчете магнитных цепей при постоянных потоках обычно используют основную кривую намагничивания. Петлеобразный характер зависимости учитывается при расчете постоянных магнитов и электротехнических устройств на их основе.
При расчете магнитных цепей на практике встречаются две типичные задачи:
-задача определения величины намагничивающей силы (НС), необходимой для создания заданного магнитного потока (заданной магнитной индукции) на каком — либо участке магнитопровода (задача синтеза
или
“прямая“ задача
);
-задача нахождения потоков (магнитных индукций) на отдельных участках цепи по заданным значениям НС (задача анализа
или
“обратная” задача
).
Следует отметить, что задачи второго типа являются обычно более сложными и трудоемкими в решении.
В общем случае в зависимости от типа решаемой задачи (“прямой” или “обратной”) решение может быть осуществлено следующими методами:
-регулярными;
-графическими;
-итерационными.
При этом при использовании каждого из этих методов первоначально необходимо указать на схеме направления НС, если известны направления токов в обмотках, или задаться их положительными направлениями, если их нужно определить. Затем задаются положительными направлениями магнитных потоков, после чего можно переходить к составлению эквивалентной схемы замещения и расчетам.
Магнитные цепи по своей конфигурации могут быть подразделены на неразветвленные
и
разветвленные.
В неразветвленной магнитной цепи на всех ее участках имеет место один и тот же поток, т.е. различные участки цепи соединены между собой последовательно. Разветвленные магнитные цепи содержат два и более контура.
Регулярные методы расчета
Данными методами решаются задачи первого типа -”прямые” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и основные геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала и магнитный поток или магнитная индукция в каком-либо сечении магнитопровода. Требуется найти НС, токи обмоток или, при известных значениях последних, число витков.
1. Прямая” задача для неразветвленной магнитной цепи
Решение задач подобного типа осуществляется в следующей последовательности:
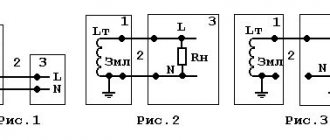
1. Намечается средняя линия (см. пунктирную линию на рис.1), которая затем делится на участки с одинаковым сечением магнитопровода.
2. Исходя из постоянства магнитного потока вдоль всей цепи, определяются значения индукции для каждого -го участка:
.
3. По кривой намагничивания для каждого значения находятся напряженности на ферромагнитных участках; напряженность поля в воздушном зазоре определяется согласно
4. По второму закону Кирхгофа для магнитной цепи определяется искомая НС путем суммирования падений магнитного напряжения вдоль контура:
,
где -длина воздушного зазора.
2. “Прямая” задача для разветвленной магнитной цепи
Расчет разветвленных магнитных цепей основан на совместном применении первого и второго законов Кирхгофа для магнитных цепей. Последовательность решения задач данного типа в целом соответствует рассмотренному выше алгоритму решения “прямой” задачи для неразветвленной цепи. При этом для определения магнитных потоков на участках магнитопровода, для которых магнитная напряженность известна или может быть вычислена на основании второго закона Кирхгофа, следует использовать алгоритм
| по |
В остальных случаях неизвестные магнитные потоки определяются на основании первого закона Кирхгофа для магнитных цепей.
В качестве примера анализа разветвленной магнитной цепи при заданных геометрии магнитной цепи на рис. 2 и характеристике ферромагнитного сердечника определим НС , необходимую для создания в воздушном зазоре индукции .
Алгоритм решения задачи следующий:
1. Задаем положительные направления магнитных потоков в стержнях магнитопровода (см. рис. 2).
2. Определяем напряженность в воздушном зазоре и по зависимости для — значение .
3. По второму закону Кирхгофа для правого контура можно записать
откуда находим и по зависимости — .
4. В соответствии с первым законом Кирхгофа
.
Тогда , и по зависимости определяем .
5. В соответствии со вторым законом Кирхгофа для искомой НС имеет место уравнение
.
Графические методы расчета
Графическими методами решаются задачи второго типа — “обратные” задачи. При этом в качестве исходных данных для расчета заданы конфигурация и геометрические размеры магнитной цепи, кривая (кривые) намагничивания ферромагнитного материала, а также НС обмоток. Требуется найти значения потоков (индукций) на отдельных участках магнитопровода.
Данные методы основаны на графическом представлении вебер-амперных характеристик линейных и нелинейных участков магнитной цепи с последующим решением алгебраических уравнений, записанных по законам Кирхгофа, с помощью соответствующих графических построений на плоскости.
1. “Обратная” задача для неразветвленной магнитной цепи
Решение задач подобного типа осуществляется в следующей последовательности:
1. Задаются значениями потока и определяют для них НС , как при решении “прямой” задачи. При этом следует стремиться подобрать два достаточно близких значения потока, чтобы получить , несколько меньшую и несколько большую заданной величины НС.
2. По полученным данным строится часть характеристики магнитной цепи (вблизи заданного значения НС), и по ней определяется поток, соответствующий заданной величине НС.
При расчете неразветвленных магнитных цепей, содержащих воздушные зазоры, удобно использовать метод пересечений, при котором искомое решение определяется точкой пересечения нелинейной вебер-амперной характеристики нелинейной части цепи и линейной характеристики линейного участка, строящейся на основании уравнения
где -магнитное сопротивление воздушного зазора.
2. “Обратная” задача для разветвленной магнитной цепи
Замена магнитной цепи эквивалентной электрической схемой замещения (см. рис. 3, на котором приведена схема замещения магнитной цепи на рис. 2) позволяет решать задачи данного типа с использованием всех графических методов и приемов, применяемых при анализе аналогичных нелинейных электрических цепей постоянного тока.
В этом случае при расчете магнитных цепей, содержащих два узла (такую конфигурацию имеет большое число используемых на практике магнитопроводов), широко используется метод двух узлов. Идея решения данным методом аналогична рассмотренной для нелинейных резистивных цепей постоянного тока и заключается в следующем:
1. Вычисляются зависимости потоков во всех -х ветвях магнитной цепи в функции общей величины -магнитного напряжения между узлами и .
2. Определяется, в какой точке графически реализуется первый закон Кирхгофа Соответствующие данной точке потоки являются решением задачи.
Итерационные методы расчета
Данные методы, сущность которых была рассмотрена при анализе нелинейных резистивных цепей постоянного тока, являются приближенными численными способами решения нелинейных алгебраических уравнений, описывающих состояние магнитной цепи. Как было отмечено выше, они хорошо поддаются машинной алгоритмизации и в настоящее время широко используются при исследовании сложных магнитных цепей на ЦВМ. При анализе относительно простых цепей, содержащих небольшое число узлов и нелинейных элементов в эквивалентной электрической схеме замещения (обычно до двух-трех), возможна реализация методов “вручную”.
В качестве примера приведем алгоритм расчета магнитной цепи на рис. 1, в которой при заданных геометрии магнитопровода, характеристике материала сердечника и величине НС F необходимо найти поток Ф.
В соответствии с пошаговым расчетом для данной цепи можно записать
| , | (1) |
где .
Задаемся значением , вычисляем для -х участков магнитопровода , по кривой намагничивания находим , подсчитываем и по (1) определяем для следующего приближения и т.д., пока с заданной погрешностью не будет выполняться равенство .
Статическая и дифференциальная индуктивности катушки с ферромагнитным сердечником
Пусть имеем катушку с ферромагнитным сердечником, представленную на рис. 4.
В соответствии с определением потокосцепления
| , | (2) |
и на основании закона полного тока , откуда
| . | (3) |
Из соотношений (2) и (3) вытекает, что функция качественно имеет такой же вид, что и . Таким образом, зависимости относительной магнитной проницаемости и индуктивности также подобны, т.е. представленные в предыдущей лекции на рис. 2 кривые и качественно аналогичны кривым и .
Статическая индуктивность катушки с ферромагнитным сердечником
;
дифференциальная индуктивность
.
Если магнитную проводимость сердечника на рис. 4 обозначить через , то и , откуда
| (4) |
Используя соотношение (4), покажем влияние воздушного зазора на индуктивность катушки.
Пусть катушка на рис. 4 имеет воздушный зазор . Тогда полное магнитное сопротивление контура
,
откуда
.
При , следовательно
.
Таким образом, воздушный зазор линеаризует катушку с ферромагнитным сердечником. Зазор, для которого выполняется неравенство , называется большим зазором.
Литература
- Основы
теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А.
Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические
основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.2. Жуховицкий Б.Я., Негневицкий И.Б. Линейные электрические цепи (продолжение). Нелинейные цепи. –М.:Энергия- 1972. –200с.
Контрольные вопросы и задачи
- Какие два типа задач встречаются при расчете магнитных цепей? Дайте им характеристику.
- Какие существуют методы расчета магнитных цепей?
- Какими методами решаются «обратные» задачи?
- Как влияет воздушный зазор на индуктивность нелинейной катушки?
- Что такое большой зазор?
- В магнитной цепи на рис. 2 заданы и . Составить алгоритм расчета длины воздушного зазора .
- Составить алгоритм итерационного расчета потока в воздушном зазоре магнитной цепи на рис. 2 при заданной НС .
- Запишите закон электромагнитной индукции с использованием статической и дифференциальной индуктивностей.
Практическое применение
Часто формулу Ома используют для ответа на следующие вопросы:
- Вычисление магнитодвижущей силы.
- Вычисление количества витков провода, которое при заданном токе обеспечит нужную величину магнитного потока.
В качестве примера рассмотрим магнитную цепь, изображенную на рисунке ниже.
Условимся, что первый участок сделан из литой стали, второй — из электротехнической, третий — это воздушный зазор. Требуется определить количество витков обмотки, способной обеспечить магнитный поток, который равен 0.0036 Вебера для тока 2 Ампера. На основании указанных на схеме размеров можно вычислить длины участков и площади сечения детали:
Чтобы найти величину магнитной индукции, в соответствующую формулу следует подставить данные из условий задачи.
Чтобы найти величину напряжённости магнитного поля, потребуется в справочнике открыть график зависимости магнитной индукции и напряжённости и определить, какая величина соответствует значению 1.5 Тесла. Для литой стали эта величина приблизительно равна 700 А/м, а для электротехнической стали — 3000 А/м. Для воздушного разрыва искомое значение можно получить при использовании соответствующей формулы:
Используя закон Ома для магнитной цепи, можно определить количество витков, подставив найденные значения:
Следовательно, в рассматриваемом случае потребуется 4083.5 витков для обеспечения нужных параметров.
Как видим, при решении практических задач в электротехнике удобно пользоваться такими понятиями, как магнитодвижущая сила и магнитное сопротивление.
Следует также сказать, что без магнитных потоков не было бы, наверное, и такой отрасли, как электротехника. Ведь на свойствах магнитного поля основывается работа многих современных устройств, среди которых трансформаторы, электрические двигатели, генераторы, измерительные приборы, разные датчики.
Магнитодвижущая сила (MMF)
Основная статья: магнитодвижущая сила
Подобно тому, как электродвижущая сила (ЭДС) управляет током электрического заряда в электрических цепях, магнитодвижущая сила (MMF) «управляет» магнитным потоком через магнитные цепи. Термин «магнитодвижущая сила», однако, неверен, поскольку это не сила и не что-либо движущееся. Возможно, лучше называть это просто MMF. По аналогии с определением ЭДС, магнитодвижущая сила F { Displaystyle { mathcal {F}}} вокруг замкнутого цикла определяется как:
F = ∮ ЧАС ⋅ d л . { displaystyle { mathcal {F}} = oint mathbf {H} cdot mathrm {d} mathbf {l}.}
MMF представляет собой потенциал, который гипотетический магнитный заряд выиграет, завершив цикл. Управляемый магнитный поток равен нет
ток магнитного заряда; он просто имеет такое же отношение к MMF, как электрический ток к EMF. (См. Подробное описание микроскопических источников сопротивления ниже.)
Единицей магнитодвижущей силы является ампер-виток (At), представленный устойчивым прямым электрический ток одного ампер протекающий в одновитковой петле электропроводящего материала в вакуум. Гилберт (Gb), установленный IEC в 1930 г.[1] это CGS единица магнитодвижущей силы и является единицей немного меньшей, чем ампер-виток. Апартамент назван в честь Уильям Гилберт (1544–1603) английский врач и натурфилософ.
1 Гб = 10 4 π В ≈ 0.795775 В { displaystyle { begin {align} 1 ; { text {Gb}} & = { frac {10} {4 pi}} ; { text {At}} & приблизительно 0,795775 ; { text {At}} end {align}}} [2]
Магнитодвижущую силу часто можно быстро рассчитать, используя Закон Ампера. Например, магнитодвижущая сила F { Displaystyle { mathcal {F}}} длинной катушки составляет:
F = N я { displaystyle { mathcal {F}} = NI}
куда N
это количество повороты и
я
это ток в катушке. На практике это уравнение используется для MMF реальных индукторы с
N
будучи номер намотки индукционной катушки.
Приложения
- В сердечниках некоторых трансформаторов могут быть созданы воздушные зазоры, чтобы уменьшить воздействие насыщенность. Это увеличивает сопротивление магнитной цепи и позволяет ей хранить больше энергия до насыщения сердечника. Этот эффект используется в обратноходовые трансформаторы видеодисплеев с электронно-лучевой трубкой и в некоторых типах импульсный источник питания.
- Изменение сопротивления — это принцип, лежащий в основе реактивный двигатель (или генератор переменного сопротивления) и Генератор Alexanderson.
- Мультимедиа музыкальные колонки обычно имеют магнитную защиту, чтобы уменьшить магнитные помехи, вызываемые телевизоры и другие ЭЛТ. Магнит динамика покрыт таким материалом, как мягкое железо для минимизации паразитного магнитного поля.
Сопротивление также может применяться к переменному сопротивлению (магнитному) пикапы.
Схемотехнические модели
Наиболее распространенный способ представления магнитной цепи — это модель сопротивления-сопротивления, которая проводит аналогию между электрическими и магнитными цепями. Эта модель хороша для систем, содержащих только магнитные компоненты, но для моделирования системы, содержащей как электрические, так и магнитные части, она имеет серьезные недостатки. Он не моделирует должным образом мощность и поток энергии между электрическими и магнитными доменами. Это связано с тем, что электрическое сопротивление рассеивает энергию, а магнитное сопротивление сохраняет ее и возвращает позже. Альтернативной моделью, которая правильно моделирует поток энергии, является гираторно-конденсаторная модель.