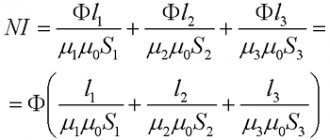ТОЭ › Расчет цепей постоянного тока
При расчете режима работы электрической цепи очень часто необходимо определить токи, напряжения и мощности на всех ее участках при заданных ЭДС источников и сопротивлений участков цепи. Данный расчёт основан на применении законов Кирхгофа.
В этой статье предполагается, что вы знакомы с определениями узла, ветви и контура.
Первый закон Кирхгофа
Первый закон Кирхгофа гласит, что в ветвях образующих узел электрической цепи алгебраическая сумма токов равна нулю (токи входящие в узел считаются положительными, выходящие из узла отрицательными).
Пользуясь этим законом для узла A (рисунок 1) можно записать следующее выражение:
Рисунок 1 — Первый закон Кирхгофа
I1 + I2 − I3 + I4 − I5 − I6 = 0.
Попытайтесь самостоятельно применить первый закон Кирхгофа для определения тока в ветви. На приведенной выше схеме изображены шесть ветвей образующие электрический узел В, токи ветвях входят и выходят из узла. Один из токов i неизвестен.
#1. Запишите выражение для узла В
Неправильно
Далее
#2. Найдите ток i
Неправильно
Завершить
Пример
Предположим, электрическая сеть состоит из двух источников напряжения и трех резисторов.
Согласно первому закону:
я1-я2-я3знак равно{\ displaystyle i_ {1} -i_ {2} -i_ {3} = 0 \,}
Применение второго закона к замкнутой цепи s
1 и замена напряжения с помощью закона Ома дает:
-р2я2+E1-р1я1знак равно{\ displaystyle -R_ {2} i_ {2} + {\ mathcal {E}} _ {1} -R_ {1} i_ {1} = 0}
Второй закон, опять же в сочетании с законом Ома, примененный к замкнутой цепи s
2, дает:
-р3я3-E2-E1+р2я2знак равно{\ displaystyle -R_ {3} i_ {3} — {\ mathcal {E}} _ {2} — {\ mathcal {E}} _ {1} + R_ {2} i_ {2} = 0}
Это приводит к системе линейных уравнений в I
1 ,
I
2 ,
I
3 :
{я1-я2-я3знак равно-р2я2+E1-р1я1знак равно-р3я3-E2-E1+р2я2знак равно{\ displaystyle {\ begin {cases} i_ {1} -i_ {2} -i_ {3} & = 0 \\ — R_ {2} i_ {2} + {\ mathcal {E}} _ {1} — R_ {1} i_ {1} & = 0 \\ — R_ {3} i_ {3} — {\ mathcal {E}} _ {2} — {\ mathcal {E}} _ {1} + R_ {2 } i_ {2} & = 0 \ end {cases}}}
что эквивалентно
{я1+(-я2)+(-я3)знак равнор1я1+р2я2+я3знак равноE1я1+р2я2-р3я3знак равноE1+E2{\ displaystyle {\ begin {cases} i_ {1} + (- i_ {2}) + (- i_ {3}) & = 0 \\ R_ {1} i_ {1} + R_ {2} i_ {2 } + 0i_ {3} & = {\ mathcal {E}} _ {1} \\ 0i_ {1} + R_ {2} i_ {2} -R_ {3} i_ {3} & = {\ mathcal {E }} _ {1} + {\ mathcal {E}} _ {2} \ end {case}}}
Предполагая
р1знак равно100Ω, р2знак равно200Ω, р3знак равно300Ω{\ Displaystyle R_ {1} = 100 \ Omega, \ R_ {2} = 200 \ Omega, \ R_ {3} = 300 \ Omega} E1знак равно3V,E2знак равно4V{\ displaystyle {\ mathcal {E}} _ {1} = 3 {\ text {V}}, {\ mathcal {E}} _ {2} = 4 {\ text {V}}}
решение
{я1знак равно11100Ая2знак равно4275Ая3знак равно-3220А{\ displaystyle {\ begin {cases} i_ {1} = {\ frac {1} {1100}} {\ text {A}} \\ i_ {2} = {\ frac {4} {275} } {\ text {A}} \\ i_ {3} = — {\ frac {3} {220}} {\ text {A}} \ end {case}}}
Ток i
3 имеет отрицательный знак, что означает, что предполагаемое направление
i
3 было неправильным, и
i
3 фактически течет в направлении, противоположном красной стрелке, обозначенной
i
3 . Ток в
R
3 течет слева направо.
Результат
Отлично!
Попытайтесь снова(
Выбор направления токов
Если при расчёте цепи направление токов неизвестны, то при составлении уравнений согласно законом Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направление токов в ветвях могут отличаться от произвольно выбранных. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчёта цепи какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным направлениям.
Например
Рисунок 2
На рисунке 2,а представлен электрический узел. Произвольно, стрелками укажем направления токов (рисунок 2,б).
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий: 1. Ток должен вытекать из узла через одну или несколько других ветвей; 2. Хотя бы один ток должен входить в узел.
Предположим, что после расчёта цепи получились следующие значения токов:
I1 = -5 А; I2 = -2 A; I3 = 3 А.
Так как значение тока I1 и I2 получились отрицательными, следовательно, действительно направление I1 и I2 противоположно ранее выбранным (рисунок 3).
Рисунок 3 — действительное направление токов обозначено синими стрелками
- I1 − I2 + I3 = 0;
- -5 − (-2) +3 = 0;
- -I1 + I2 + I3 = 0;
- -5 + 2 +3 = 0.
История
Пополнил ряды немецких ученых Кирхгоф в девятнадцатом столетии, когда в стране, находившаяся на пороге революции индустриальной, требовались новейших технологии. Ученые занимались поиском решений, которые могли бы ускорить развитие промышленности.
Активно занимались исследованиями в области электричества, поскольку понимали, что в будущем оно будет широко использоваться. Проблема состояла на тот момент не в том, как составлять электрические цепи из возможных элементов, а в проведении математических вычислений. Тут и появились законы, сформулированные физиком. Они очень помогли.
К узлу подходят 2 провода, а отходит один. Значение тока, текущего от узла, такое же, как сумма его, протекающего по двум остальным проводникам, т.е. идущим к нему. Правило Кирхгофа объясняет, что, при ином раскладе, накапливался бы заряд, но такого не бывает. Все знают, что всякую сложную цепь легко разделить на отдельные участки.
Но, при этом непросто определить путь, по которому он проходит. Тем более, что на различных участках сопротивления не одинаковы, поэтому и распределение энергии не будет равномерным.
В соответствие со Вторым правилом Кирхгофа, энергия электронов на каждом из замкнутых участков электрической цепи равняется нулю – нулю равняется всегда в таком контуре суммарное значение напряжений. Если бы нарушилось данное правило, энергия электронов при прохождении определенных участков, уменьшалась бы или увеличивалась. Но, этого не наблюдается.
Ограничения
Законы Кирхгофа для схемы являются результатом модели с сосредоточенными элементами, и оба зависят от модели, применимой к рассматриваемой схеме. Когда модель неприменима, законы не применяются.
Текущий закон зависит от предположения, что чистый заряд в любом проводе, соединении или сосредоточенном компоненте постоянен. Когда электрическое поле между частями схемы не является незначительным, например, когда два провода имеют емкостную связь , это может быть не так. Это происходит в высокочастотных цепях переменного тока, где модель с сосредоточенными элементами больше не применима. Например, в линии передачи плотность заряда в проводнике будет постоянно колебаться.
В линии передачи чистый заряд в разных частях проводника изменяется со временем. В прямом физическом смысле это нарушает KCL.
С другой стороны, закон напряжения основан на том факте, что действие изменяющихся во времени магнитных полей ограничено отдельными компонентами, такими как индукторы. В действительности индуцированное электрическое поле, создаваемое индуктором, не ограничено, но поля утечки часто незначительны.
Моделирование реальных схем с сосредоточенными элементами
Приближение сосредоточенных элементов для схемы является точным на низких частотах. На более высоких частотах утечки потоков и различные плотности заряда в проводниках становятся значительными. До некоторой степени все еще возможно моделировать такие схемы, используя паразитные компоненты . Если частоты слишком высоки, может быть более целесообразным моделировать поля напрямую, используя моделирование методом конечных элементов или другие методы .
Чтобы смоделировать схемы, чтобы можно было использовать оба закона, важно понимать разницу между физическими элементами схемы и идеальными элементами с сосредоточенными параметрами. Например, провод — не идеальный проводник
В отличие от идеального проводника, провода могут индуктивно и емкостно соединяться друг с другом (и с самими собой) и иметь конечную задержку распространения. Реальные проводники можно моделировать в терминах сосредоточенных элементов, учитывая паразитные емкости, распределенные между проводниками, для моделирования емкостной связи или паразитные (взаимные) индуктивности для моделирования индуктивной связи. Провода также имеют некоторую самоиндукцию, поэтому необходимы разделительные конденсаторы .
Примеры решения задач по электродинамике
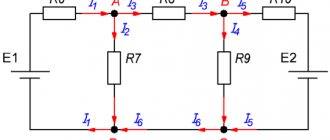
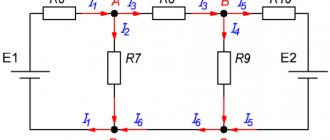
Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неизвестных токов шесть и система должна состоять из шести уравнений.
Из простых физических соображений выводятся 1 и 2 правила Киргофа, являющиеся основой для расчета токов…
Начало ТОЭ. Метод узловых потенциалов. Показан пример решения задач по ТОЭ методом узловых потенциалов….
Поскольку неизвестны значения трех сил токов, то минимальным количеством уравнений для решения задачи есть три.
Как мы помним, закон Ома связывает между собой ток, напряжение и сопротивление. Если нам известны любые две из этих величин, мы легко можем найти третью. В данном случае мы знаем сопротивление и ток, который течет через это сопротивление.
В этих уравнениях значение ЭДС берется со знаком «+», если направление ЭДС совпадает с направлением обхода контура.
Но чем сложнее схема, тем с большим количеством преобразований придется столкнуться. К примеру, сначала схему необходимо будет свернуть до одного контура, найти необходимые значения, затем постепенно её разворачивать производя все новые и новые вычисления.
Совместное решение любых трех уравнений (1-21а) и уравнений (1-23) и (1 -24) дает значения токов во всех ветвях электрической цепи, показанной на рис. 1-18, а.