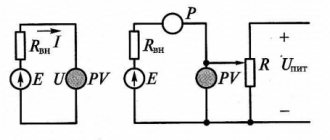
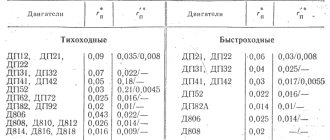
Есть двигатель постоянного тока. Задача — разработать, собрать и протестировать устройство, позволяющиее реализовать контур тока применительно к этому двигателю. Желаемое время переходного процесса на застопоренном двигателе (без противо-ЭДС) — не более 10мс. Интерфес связи с внешним управляющим контроллером — SPI. Двигатель постоянного тока, коллекторный, максимальное напряжение 24В, рабочий ток до 5А.
Что значит — контур тока? Самые распространённые драйверы для управления двигателями это всякие вариации полумостов, которые усиливают напряжение. А мне хочется, чтобы драйвер брал на вход не напряжение, а силу тока. Сила, развиваемая электроприводом, прямо пропорциональна силе протекающего тока. А значит, и прямо пропорциональна ускорению на валу двигателя. Такой контур тока позволит избежать извращений, на которые нужно идти без него, как я это делал тут.
Я разбил этот текст на две статьи:
- 1. Измерение сопротивления и индуктивности двигателя
- 2. Разработка управляющего контура
Вот так выглядит макет управляющего железа:
В состав системы будут входить:
- Силовая микросхема ключей, принимающая входной PWM сигнал и усиливающая его.
- Датчик тока.
- Управляющий микроконтроллер, реализующий обратную связь и закон управления.
Датчик тока и его проверка
В качестве датчка тока выбран датчик Холла Allegro ACS714 ($3), выдающий аналоговый сигнал с центром в 2.5В и 185мВ/А, типичная ошибка 1.5%. На датчик была добавлена RC-цепочка в качестве фильтра низких частот с частотой среза 16кГц.
Датчик тока был запитан от 4.96В источника, последовательно с датчиком был подключен резистор, через который было пропущено 2А. Теоретическое напряжение на выходном пине должно быть 4.96/2 + (2 * 0.185 +- 1.5%), измерение показало 2.84 В, что укладывается в расчётные параметры. Затем было поменяно направление течения тока через резистор, при -2А измеренное напряжение на выходном пине датчика составило 2.11В, что опять укладывается в расчётные параметры:
Эта проверка была необходима, т.к. я купил несколько макеток с ACS712 и ACS714 от разных производителей, и в параметры даташита попал только один!
Сопротивление обмоток: классификация машин, строение моторов
Электрические машины, применяемые в быту и на производстве, классифицируются. Существуют генераторы, электродвигатели, осуществляющие преобразование электроэнергии в механическую, и специализированные машины, преобразующие энергию одного вида в ресурс другого. Задача первых заключается в преобразовании механической в электрическую энергию.
По конструкционному исполнению электродвигатели бывают коллекторными и бесколлекторными. Первые – электромашины, использующие постоянный ток, т.е. их можно задействовать в качестве генераторных установок. Гораздо реже их применяют для работы с постоянным током – однофазные агрегаты небольшой мощности. Бесколлекторные электродвигатели – силовые машины, работающие, в большинстве случаев, исключительно на переменном токе. По принципу действия делятся на:
- асинхронные двигатели – основная специфика эксплуатации примечательна использованием, как электромоторы;
- синхронные моторы – их применяют как генераторы, так и в качестве электродвигателей.
На шильдике, расположенном на корпусе мотора, указаны номинальные технические характеристики, схема подключения обмоток, сопротивление элементов асинхронного оборудования: двигателя, комплексных систем. Один из важнейших параметров – мощность электродвигателя. Данная характеристика определяет механическую мощность, которая развивается на валу в рамках номинального режима функционирования. В генераторах под этой величиной понимают мощность электродвигателя, отдаваемая во внешнюю цепь инфраструктуры.
Строение асинхронных двигателей
Этот тип электрических моторов наиболее распространен ввиду относительно простой конструкции, высоким рабочим характеристикам, которые можно контролировать, стоимости. Функциональные возможности и номинальные параметры позволяют использовать асинхронные устройства во всех сферах деятельности, включая высокосложное производство, сельское хозяйство, транспортную инфраструктуру.
Типовая конструкция асинхронных машин с короткозамкнутой подвижной частью:
- неподвижная часть – сердечник, две обмотки статора, станина. Статорный сердечник – составной элемент, входящий в комплекс магнитопривода машины. Представляет собой полый цилиндр, в котором расположены пазы осевого направления. Пазы сердечника предназначены для расположения трехфазных обмоток статора – производятся с применением изолированного медного провода, гораздо реже – из алюминиевого провода;
- коробка выводов;
- воздушный зазор, отделяющий элементы;
- сердечник подвижного механизма (ротора);
- подшипниковый щит.
Концы обмоток статора соединены зажимами – размещены в коробке с выводами на корпусе электродвигателя. На вывод подаются шесть концов обмоток так, как это позволяет эксплуатировать электродвигатель при различных напряжения электроснабжения.
Роторный сердечник – также часть магнитопровода. Представлен спрессованными тонкими листами электротехнической стали. Как и в случае со статором, имеет форму цилиндра, но с продольными пазами в наружной части, оснащен отверстием для расположения вала.
Интересно: Машины, имеющие фазную подвижную часть – агрегаты, использующиеся реже короткозамкнутых. Это обусловлено повышенной ценой, дорогим техническим обслуживанием, меньшей надежностью. Их задействуют для обустройства приводов установок, в которых существенно усложнены условия пуска. Моторы с фазной подвижной частью довольно часто встречаются при обустройстве систем, требующих повышенную плавность, глубокую регулировку технических характеристик силовых приспособлений.
Крановые электрические моторы и асинхронные машины (АМ) высокой частоты
Силовые установки отличительны свойствами, за счет которых агрегаты выдерживают кратковременные и повторно-кратковременные нагрузки с частыми пусками, торможением и значительными объемами перегрузок. Такие агрегаты имеют повышенную механическую прочность, сопротивление изоляции к нагреву двигателя, работающего по асинхронному принципу.
Установки в кранах примечательны пониженной инерционностью вращающихся частей, перегрузочной способностью. Все это позволяет эксплуатировать моторы в крайне сложных условиях технического процесса.
Асинхронные моторы повышенной частоты задействуют для обустройства приводов электрических инструментов. Мощность электродвигателя небольшая, масса незначительная, но частота оборотов повышена. Для такого оборудования актуальны короткозамкнутые моторы – дополнительная очистка от абразивов, пыли, возникающих при осуществлении технического процесса, обеспечивается закрытым обдувом. Магнитопроводы обустраиваются тонкими листами электротехнической маркированной стали.
Микроконтроллер
В качестве управляющего микроконтроллера выбран ATMega328p, работающий на частоте 16МГц. Обвязка микроконтроллера — китайский клон Arduino Nano v3 ($1.5).
Микроконтроллер генерирует ШИМ сигнал через восьмибитный счётчик с делителем 8, таким образом, частота ШИМ сигнала 16 * 10^6 /255 /8 = 7.8 кГц, что укладывается в максимально доступные для драйвера 20кГц.
Делитель АЦП микроконтроллера установлен на 128; поскольку каждое измерение требует примерно 13 тактов, максимальная частота измерений протекающего тока равна примерно 16 * 10^6 / 128 / 13 = 9.6 кГц. Измерения производятся в фоновом режиме, извещая основную программу об окончании при помощи вызова соответствующего прерывания.
Расчет мощности трехфазной сети
Электрическая энергия на все объекты изначально поступает через трехфазную сеть. В частные дома она может заводиться напрямую, а в многоквартирном доме доходит лишь до вводного распределительного устройства. Далее по квартирам расходятся уже однофазные линии. В любом случае потребуется выполнить расчет мощности трехфазной сети, чтобы заранее определить ее способность выдерживать запланированные нагрузки по току.
Для того чтобы сделать правильные вычисления, нужно знать особенности таких сетей, принципы их работы и технические характеристики. Все необходимые расчеты выполняются вручную при помощи формул или с использованием онлайн-калькулятора.
Логи
Я долго бился над тем, как записывать происходящее внтри микроконтроллера, ведь памяти у него совсем немного. В итоге я обнаружил, что родной SPI интерфейс очень быстрый, и в итоге вся отладочная информация передаётся микроконтроллером по интерфейсу SPI, для её записи был применён широкодоступный ($10 на дилэкстриме, $6 на алиэкспрессе) китайский клон логического анализатора Saelae Pro 8 Logic. После совсем нетрудных манипуляций по перепрошивке VID/PID, он может быть использован с родным софтом от Saelae. Я пользуюсь sigrok (pulseview). У него исключительно простой формат лог-файлов, которые я просто читаю своей самописной программкой в пятьдесят строк. Я купил этот анализатор по совету gbg, который мне дистанционно чинил мой спектрум (спасибо тебе огромное!), и считаю это самым выгодным вложением денег за последние два года.
Например, я подал синусоидальный сигнал (в ШИМ) на выход контроллера, и логический анализатор его прекрасно видит:
Всё это было соединено вместе, фотография дана в заголовке поста.
Практически все статьи, что я размещаю здесь, являются моим рабочим дневником. Я чему-то учусь (в данном случае теории управления) и старательно записываю то, что узнал. Лучший способ записать — это написать объяснение того, как это всё работает. Затем статьи выкладываю на разных площадках, например тут.
Целей при написании текста у меня две:
а) получить обратную связь от людей, которые знают больше меня.
Например, практически всё, что я узнал для данных двух статей, мне рассказал уважаемый Arastas, прошу любить и жаловать: человек, который тратит личное время на обучение таких оболтусов, как я.
Опять же, gbg, который написал мне линейную алгебру для моих лекций по компьютерной графике, а потом за много тысяч километров по телефону дебажил мне электронику.
б) просто записать:
таким образом я получаю библиотеку личного опыта, к которой периодически возвращаюсь.
Кстати, тематические медиа, какой процент авторов соглашаются на ваши условия программы поддержки?
Преобразование Фурье
Первое, что нужно понять, читая мои тексты: я считаю, что функция и вектор — это одно и то же. Все разговоры про бесконечности на меня навевают скуку и заслоняют суть происходящего. Обобщённые функции и тому подобное — это способ рассмотреть патологические случаи используя тот же самый язык, что и случаи, где никаких патологий нет. Вот только патологии меня не интересуют.
На эту тему хорошо высказался Валерий Иванович Опойцев (Босс):
В любой области полезно оказаться в подходящей среде устного общения, где осыпается книжная шелуха. Там иногда ничего не меняется по сути, зато возникает чувство попадания в колею и освобождения от догм. Для науки, которая всегда в маске, это особенно важно. Суть за кадром, перед глазами — кружева. И вечно чего-то не хватает. То простоты, то сложности, да точно и не определишь — чего. Что-то куда-то шагает, ты — на обочине, а время уходит в песок, не говоря о жизни.
Далее предпринимается попытка сдвинуть ситуацию с места, моделируя письменную среду, где «спадают покровы». Внешняя канва содержания более-менее неясна из оглавления, но главная цель — та, что за кадром. Снять вуаль, грим, убрать декорации. Переупростить, даже приврать слегка, ибо дозирование правды — краеугольный камень объяснения. Результаты, перегруженные деталями, не пролезают куда надо. Озарение случается, когда пухнущая голова проваливается на уровень «дважды два», в то время как счет идет на миллионы. Такая уж тут диалектика.
Если у нас есть вектор (7,12,18,-2), то его можно рассматривать как набор коэффициентов во взвешенной сумме. 7*(1,0,0,0) + 12*(0,1,0,0) + 18*(0,0,1,0) + (-2)*(0,0,0,1). Ровно так же можно считать этот вектор значениями функции в точках 0, 1, 2, 3, ведь наши векторы (0,1,0,0) и ему подобные можно рассматривать как сдвиг единичного импульса: Если постоянно увеличивать количество векторов (сдвинутых единичных импуьсов) в базисе, то получим обычные функции.
К сожалению, с таким базисом бывает довольно неудобно работать. Давайте рассмотрим следующую функцию в качестве примера:
Мы уже беседовали о том, что такое преобразование Фурье. Если кратко, то это смена базиса.
В нашем случае преобразование Фурье — это функция из вещественных чисел в комплексные:
Аргумент функции (вещественное число) — это просто номер базисной функции или вектора (на самом деле, пары базисных функций), а её значение — это соответствующая (пара) координат в для этих двух векторов в базисе. Базис Фурье — это синусы и косинусы различных частот. Частота и является номером базисной функции.
Для нашей конкретной функции f(t), которая уже являетя взвешенной суммой синуса и косинуса, очень легко посчитать её разложение в базис Фурье:
То есть, наша функция f(t) имеет нулевые координаты для всех векторов базиса, кроме векторов номер 11 и 41.
Чем полезен базис Фурье? Например тем, что операция дифференцирования линейно преобразует этот базис. Допустим, мы хотим посчитать преобразование Фурье от производной f'(t). Как это сделать? Как вариант, в лоб: сначала посчитать производную, а затем посчитать преобразование Фурье:
Очевидно, что при дифференцировании sin(x) он станет sin(x+90°), то есть крайне легко найти соответствие разложение в базис Фурье исходной функции и её производной: Умножение на
i
— это просто поворот комплексной плоскости, который соответствует +90° в аргументе нашей функции. То есть, операция дифференцирования, которую сложно делать в базисе единичных импульсов, в базисе Фурье — это просто масштабирование и поворот на 90 градусов. Красиво, правда?
Преобразование Лапласа
Примерно та же самая история происходит и с преобразованием Лапласа. К сожалению, в отличие от базиса Фурье, базис Лапласа неортогонален, поэтому для интуитивного понимания чуточку более сложен. Ну да не суть. Лаплас пошёл немного дальше. Если у Фурье в базисе были только синусоиды, то у Лапласа в базисе синусоиды с экспоненциальным затуханием. Откуда он их взял? Это крайне, крайне полезно при решении линейных дифференциальных уравнений. Давайте подумаем, какая функция преобразуется сама в себя при дифференцировании? Экспонента. А при дифференцировании два раза? Синус. А их комбинации дают все возможные функции, которые могут появиться при решении (линейных) диффуров, что и использовал маркиз дё Лаплас.
Не будем вдаваться в подробности того, как выводятся эти свойства (лучше рассмотрите внимательно свойства базиса Фурье, он проще), давайте просто отметим следующие факты:
1. Преобразование Лапласа линейно:
2. Преобразование Лапласа производной — это аффинное действие над преобразованием самой функции: 3. Итак, если у нас есть двигатель постоянного тока, то протекающий ток I(t) и напряжение на клеммах U(t) связаны следующим дифференциальным уравнением, где w(t) — это скорость вращения вала двигателя: Здесь L — это индуктивность, а R — сопротивление, которые мы и ищем. Я не буду повторять, откуда вылезает этот диффур, так как уже подробно и на пальцах его расписывал (см. «уравнения Максвелла на пальцах»).
Поскольку наша задача найти L и R, давайте жёстко зафиксируем вал двигателя, таким образом заставив w(t) быть нулевой:
По совету Arastas я подал два типа сигналов на мой двигатель: меандр и синусоиду. Затем я измерил протекающий ток, картинка получается примерно следующая:
Здесь синие кривые — это входное напряжение, котороя я контролирую, а зелёные — это измерения силы тока, полученные при помощи ACS714.
Мой микроконтроллерный код, который генерирует 11 экспериментов с меандром и синусоидами различных амплитуд и частот, можно посмотреть здесь.
Давайте решим наше дифференциальное уравнение для обоих типов сигнала напряжения, получим параметрический выходной сигнал силы тока, и подберём параметры, чтобы теоретическая кривая как можно лучше аппроксимировала реальные измерения.
Подготовка к обмеру электродвигателя перед перемоткой.
При подготовке, перед тем как приступить к обмеру, следует тщательно очистить сердечник статора (а если надо, то и ротора) от грязи и масла, остатков старой обмотки и ее изоляции, слоев лака, краски, ржавчины и т. п. При очистке сердечника статора не следует применять напильник даже и с мелкой насечкой. Лучше всего пользоваться только тряпкой, смоченной в керосине; в крайнем случае, крепко приставшие частицы удаляются шабером. Внутренность пазов удобно протирать веревкой, смоченной в керосине. После очистки сердечник обтирается насухо чистой ветошью.
Входной сигнал — функция Хэвисайда (полупериод меандра)
Итак, w(t) = 0, начальные условия I(0) = 0, ток в самом начале не течёт. Приложим постоянное напряжение U0 к клеммам мотора, как себя должен будет вести протекающий ток?
Давайте возьмём преобразование Лапласа от левой и правой частей дифференциального уравнения (1):
Для получения второй строчки я использовал линейность преобразования Лапласа, U0/s — взял из таблицы (обычно преобразования Лапласа вручную не считают, пользуются таблицами).
Для получения третьей строки использовано свойство производной.
Последняя строчка получается из предпоследней использованием метода неопределённых декомпозиций. Смысл этого перехода в том, чтобы опять получить табличную функцию. Разумеется, в двадцать первом веке руками это считать ни к чему.
Теперь осталось применить обратное преобразование Лапласа (для правой части мы смотрим таблицу) и мы решили наш диффур. Переход в базис Лапласа превратил дифференциальное уравнение в обычное алгебраическое!
Быстрая проверка результата: по истечении нескольких миллисекунд индуктивность уже не будет играть роли, и мы получим протекающий ток U_0 / R (закон Ома). В самом же начале протекающий ток равен нулю и экспоненциально возрастает, причём скорость возрастания напрямую зависит от индуктивности. Sanity check passed.
Файл с измерениями лежит здесь. Три колонки, секунды, приложенное напряжение (в вольтах), измеренная сила тока (в амперах).
Вот код, который подбирает параметры сопротивления и индуктивности для этого эксперимента:
Скрытый текст
import numpy as np from scipy.optimize import curve_fit import matplotlib.pyplot as plt U0 = 19.2 def unit_step_current(x, R, L): return [U0/R — U0/R*np.exp(-t*R/L) for t in x] data = np.genfromtxt(‘unit_step_19.2V.csv’, delimiter=’,’, names=[‘t’, ‘V’, ‘A’]) [R, L] = curve_fit(unit_step_current, data[‘t’], data[‘A’])[0] print(R, L) fig = plt.figure() ax1 = fig.add_subplot(1,1,1) ax1.set_title(«Resistance/inductance fitting») ax1.set_xlabel(‘Time, seconds’) ax1.set_ylabel(‘Current (A), tension (V)’) ax1.plot(data[‘t’], data[‘V’], color=’b’, label=’input tension’) ax1.plot(data[‘t’], data[‘A’], color=’g’, label=’measured current’) model=unit_step_current(data[‘t’], R, L) ax1.plot(data[‘t’], model, color=’r’, label=’fitted curve’) ax1.legend() plt.show()
Он говорит, что хорошо подходит пара R=4.4 Ома, L=6мГенри, вот график:
Использование калькулятора для расчета мощности
Онлайн-калькулятор существенно ускоряет проведение расчетов мощности в трехфазной сети. Для этого должны быть заранее известны мощность и характер нагрузки – активной и реактивной, сетевое напряжение, а также тип сети – одно- или трехфазный. Все параметры рассчитываются по формулам и методикам, приведенным выше. Достаточно всего лишь вставить в окна необходимые данные и нажать кнопку «Рассчитать ток». В окне с обозначением тока в А появится искомый результат, показывающий величину тока по мощности.
Входной сигнал — синус
Повторим процедуру для синусоиды напряжения с амплитудой U0 и частотой F0. Применим преобразование Лапласа к уравнению (1), сначала к правой части: а потом и к левой: Теперь обратное преобразование нам даст следующий закон протекания тока: Опять быстрый sanity check: нулевой ток в самом начале, несколько миллисекунд переходных процессов (экспонента, напрямую зависящая от индуктивности). По истечению некоторого времени протекающий ток — это взвешенная сумма синуса и косинуса одной и той же частоты (частота равна входной, это хорошо). Эта сумма даёт синусоиду, чуть сдвинутую во времени. Отлично, результат правдоподобен.
Измерения лежат здесь, а код подбора параметров тут. Он даёт примерно такие же значения сопротивления и индуктивности, что нам и требовалось. Вот график:
Почему не измерить параметры напрямую, зачем весь этот огород с микроконтроллерами? Во-первых, мне нечем измерять индуктивность. Да и измерение сопротивления двигателя омметром может иметь свои нюансы.
Далее, параметры, найденные при высокой амплитуде сигнала, не совсем совпадают с тем, что получается при низких напряжениях. Может быть интересно (тут не рассмотрено) делать модель не только двигателя, а всей системы в целом, включая нелинейность ШИМ-драйвера.
Ну а дальше осталось разработать регулятор, который будет на вход брать необходимую силу тока. Оставайтесь на связи!
Расчет мощности потребителей
В первую очередь нужно заранее установить объемы потребляемой электроэнергии. Для этого суммируется мощность всех потребителей, находящихся в доме. Сюда входит мощное оборудование, обычная бытовая техника и осветительные приборы. У некоторых хозяев этот список может быть дополнен теплыми электрическими полами.
Все необходимы сведения можно посмотреть в техническом паспорте, который прилагается к каждому устройству. На некоторые приборы наносится соответствующая маркировка. Вначале идут самые мощные агрегаты и далее – все остальное оборудование, по мере уменьшения мощности.
Для вычислений берется стиральная машина-автомат, мощностью 2600 Вт, электрический водонагреватель – 1900 Вт, утюг – 1500 Вт, пылесос – 1000 Вт, микроволновка – 800 Вт, компьютер и оргтехника – 600 Вт, осветительные приборы (с лампами эконом) – 400 Вт, холодильник – 300 Вт, телевизор – 100 Вт. Итоговый результат получился 9200 Вт и его необходимо перевести в киловатты. Для этого 9200 Вт делится на 1000, получается 9,2 кВт, что и будет расчетным потреблением электроэнергии.
С данной мощностью может справиться и одна фаза, однако в частных домах устанавливается более мощное оборудование, для работы которого лучше пользоваться сетями 380в. В этом случае гарантируется бесперебойное функционирование отопительных и водонагревательных котлов, насосов, электродвигателей и других агрегатов.