Измерение частоты, индуктивности и ёмкости в электрических цепях

Любители электроники наверняка знакомы с таким прибором как мультиметр, с помощью которого можно измерять напряжение, ток, сопротивление и т.д. Со всем этим мультиметр справляется достаточно легко. Но иногда у любителей электроники возникает необходимость измерения индуктивности и емкости и с этой задачей уже не справится обычный мультиметр. Для этой цели созданы специализированные мультиметры, но они стоят значительно дороже обычных.

На нашем сайте мы уже рассматривали создание измерителя емкости, измерителя частоты и измерителя сопротивления (омметра) на основе платы Arduino. А в этой статье мы рассмотрим создание измерителя емкости и индуктивности (Inductance LC Meter) на основе платы Arduino. Измеренные значения емкости и индуктивности мы будем показывать на экране ЖК дисплея 16х2. Кнопка в схеме проекта будет использоваться для переключения между режимом измерения емкости и индуктивности.

Необходимые компоненты

1. Плата Arduino Uno (купить на AliExpress).
2. Микросхема операционного усилителя 741.
3. ЖК дисплей 16х2 (купить на AliExpress).
4. Батарея на 3v (для питания операционного усилителя) и источник питания для остальной части схемы.
5. Резистор 100 Ом (купить на AliExpress).
6. Конденсаторы (купить на AliExpress).
7. Индуктивности.
8. Диод 1n4007 (купить на AliExpress).
9. Резистор 10 кОм (купить на AliExpress).
10. Потенциометр 10 кОм (купить на AliExpress).
11. Кнопка.
12. Макетная или печатная плата и соединительные провода.

Внешний вид некоторых из использованных в проекте компонентов показан на следующем рисунке.

Как произвести пересчет катушек индуктивности (однослойных, цилиндрических)

Необходимость в пересчете катушек индуктивности возникает при отсутствии нужного диаметра провода, указанного в описании конструкции, и замене его проводом другого диаметра; при изменении диаметра каркаса катушки.

Если отсутствует провод нужного диаметра, что является наиболее частой причиной пересчета катушек, можно воспользоваться проводом другого диаметра.

Изменение диаметра провода в пределах до 25% в ту или другую сторону вполне допустимо и в большинстве конструкций не отражается на качестве их работы. Более того, увеличение диаметра провода допустимо во всех случаях, так как оно уменьшает омическое сопротивление катушки и повышает ее добротность.

Уменьшение же диаметра ухудшает добротность и увеличивает плотность тока на единицу сечения провода, которая не может быть больше определенной допустимой величины.

Пересчет числа витков однослойной цилиндрической катушки при замене провода одного диаметра другим производится по формуле:

где:

• n — повое число витков катушки;
• n1 — число витков катушки, указанное в описании;
• d— диаметр имеющеюся провода;
• d1 — диаметр провода, указанный в описании.

В качестве примера произведем пересчет числа витков катушки, изображенной на рис. 1, для провода диаметром 0,8 мм:

(длина намотки l= 18 X 0,8 = 14,4 мм, или 1,44 см).

Таким образом, число витков и длина намотки несколько уменьшились. Для проверки правильности пересчета рекомендуется выполнить новый расчет катушки с измененным диаметром провода:

При пересчете катушки, связанном с изменением ее диаметра, следует пользоваться процентной зависимостью между диаметром и числом витков катушки.

Эта зависимость заключается в следующем: при увеличении диаметра катушки на определенное число процентов количество витков ее уменьшается на столько же процентов, и, наоборот, при уменьшении диаметра увеличивается число витков на равное число процентов. Для упрощения расчетов за диаметр катушки можно принимать диаметр каркаса.

Рис. 2. Катушки индуктивности. Пример.

Так, для примера произведем пересчет числа витков катушки (рис. 2, а), имеющей диаметр 1,5 см, на диаметр, равный 1,8 см (рис. 2, б). Согласно условиям пересчета диаметр каркаса увеличивается на 3 мм, или на 20%.

Следовательно, для сохранения неизменной величины индуктивности этой катушки при намотке ее на каркасе большего диаметра нужно уменьшить число витков на 20%, или на 8 витков. Таким образом, новая катушка будет иметь 32 витка.

Проверим пересчет н установим погрешность, допущенную в результате пересчета. Катушка (см. рис. 2, а) имеет индуктивность:

Новая катушка на каркасе с увеличенным диаметром:

Ошибка при пересчете составляет 0,25 мкГн, что вполне допустимо для расчетов в радиолюбительской практике.

Расчет частоты и индуктивности

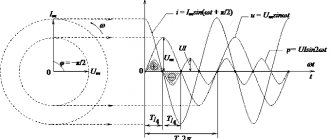
В этом проекте мы будем измерять емкость и индуктивность с помощью LC цепи, включенной параллельно – то есть, по сути, это хорошо известный нам LC контур. Эту цепь можно сравнить со звонком, который начинает резонировать на определенной частоте. При подаче на эту цепь импульса она начинает резонировать и на ее выходе образуется синусоидальное колебание на резонансной частоте. Это синусоидальное колебание нам необходимо преобразовать в прямоугольную волну. Для этого мы будем использовать операционный усилитель на микросхеме 741, который будет преобразовывать синусоидальное колебание в последовательность прямоугольных импульсов с коэффициентом заполнения 50%. Затем мы будем измерять частоту этих импульсов с помощью платы Arduino и затем с помощью ряда математических преобразований мы можем определить измеряемые индуктивность или емкость. Для этого мы будем использовать обычную формулу, связывающую частоту и время для прямоугольной волны:

f=1/(2*time)

где time (время) будет определяться с помощью функции pulseIn() .

Также нам известна формула для расчета частоты LC контура:

f=1/2*Pi* square root of (LC)

square root – квадратный корень.

Из этого выражения мы можем выразить индуктивность L:

f2 = 1/ (4Pi2LC) L= 1/ (4Pi2 f2C) L = 1/(4* Pi * Pi * f * f * C)

Поскольку синусоидальная волна с выхода LC контура имеет одинаковую длительность положительность и отрицательной полуволны, то компаратор на основе операционного усилителя преобразует ее в прямоугольную волну (последовательность прямоугольных импульсов) с коэффициентом заполнения 50% — мы можем измерить частоту этой прямоугольной волны с помощью функции pulseIn() в Arduino. Эта функция определит нам временной период, который мы затем переведем в значение частоты с помощью выше приведенной формулы. Поскольку функция pulseIn измеряет только один импульс, поэтому чтобы получить правильное значение частоты мы его в формуле умножаем на 2. А когда у нас значение частоты, мы с помощью формулы для LC контура определим значение индуктивности.

Примечание: во время измерения индуктивности (L1) емкость C1) в нашем проекте должна быть 0.1 мкФ, а во время измерения емкости (C1) индуктивность (L1) должна быть равна 10 мГн. Если вы хотите изменить эти значения, то вам необходимо будет внести соответствующие изменения в код программы.

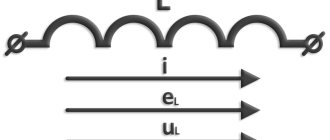
Индуктивность соленоида

Катушка в форме соленоида (конечной длины).

Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция) B{\displaystyle B}, которая выражается в системе СИ в тесла , внутри катушки является фактически постоянной и (приближённо) равна

B=μNil{\displaystyle \displaystyle B=\mu _{0}Ni/l}

или

B=μni,{\displaystyle \displaystyle B=\mu _{0}ni,}

где μ{\displaystyle \mu _{0}} − магнитная постоянная, N{\displaystyle N} − число витков, i{\displaystyle i} − ток, записанный в амперах , l{\displaystyle l} − длина катушки в метрах и n{\displaystyle n} — плотность намотки витков в . Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B{\displaystyle B} , умноженному на площадь поперечного сечения S{\displaystyle S} и число витков N{\displaystyle N}:

Ψ=μN2iSl=μn2iV,{\displaystyle \displaystyle \Psi =\mu _{0}N^{2}iS/l=\mu _{0}n^{2}iV,}

где V=Sl{\displaystyle V=Sl} − объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):

L=μN2Sl=μn2V.{\displaystyle \displaystyle L=\mu _{0}N^{2}S/l=\mu _{0}n^{2}V.}

Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель μ{\displaystyle \mu } — относительную магнитную проницаемость сердечника:

L=μμN2Sl=μμn2V.{\displaystyle \displaystyle L=\mu _{0}\mu N^{2}S/l=\mu _{0}\mu n^{2}V.}

В случае, когда μ>>1{\displaystyle \mu >>1}, можно (следует) под S

понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Работа схемы

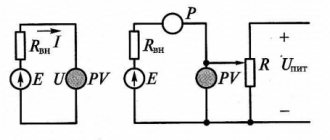
Схема измерителя емкости и индуктивности на основе платы Arduino представлена на следующем рисунке.

Плата Arduino в этой схеме управляет всеми процессами. Для измерения емкости или индуктивности используется LC контур, состоящий из конденсатора и катушки индуктивности. Для преобразования синусоидальной волны с выхода LC в прямоугольную волну мы использовали операционный усилитель на микросхеме 741. Для этого мы должны подать отрицательное напряжение питания на операционный усилитель – с этой целью мы используем батарейку на 3 В, соединенную в отрицательной полярности. Это означает что отрицательный контакт микросхемы 741 подключен к отрицательному контакту батареи, а положительный контакт батареи подключен к земле схемы.

Кнопка в схеме используется для смены режима – измерения емкости или индуктивности. ЖК дисплей используется для отображения результатов измерений. Потенциометр предназначен для управления яркостью ЖК дисплея. Схема запитывается от контакта 5v платы Arduino, а саму плату Arduino можно запитать через USB кабель от компьютера или с помощью адаптера на 12 В.

Внешний вид собранной на макетной плате схеме показан на следующих рисунках, а также на них показан пример работы схемы в режиме измерения емкости и в режиме измерения индуктивности.

Индуктивность соленоида

Катушка в форме соленоида (конечной длины).

Соленоид — катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного сердечника плотность магнитного потока (или магнитная индукция) B{\displaystyle B}, которая выражается в системе СИ в тесла , внутри катушки вдали от её концов (приближённо) равна

B=μNil{\displaystyle \displaystyle B=\mu _{0}Ni/l}

или

B=μni,{\displaystyle \displaystyle B=\mu _{0}ni,}

где μ{\displaystyle \mu _{0}} − магнитная постоянная, N{\displaystyle N} − число витков, i{\displaystyle i} − ток в амперах , l{\displaystyle l} − длина катушки в метрах и n{\displaystyle n} — плотность намотки витков в . Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно плотности потока B{\displaystyle B} , умноженному на площадь поперечного сечения S{\displaystyle S} и число витков N{\displaystyle N}:

Ψ=μN2iSl=μn2iV,{\displaystyle \displaystyle \Psi =\mu _{0}N^{2}iS/l=\mu _{0}n^{2}iV,}

где V=Sl{\displaystyle V=Sl} − объём катушки. Отсюда следует формула для индуктивности соленоида (без сердечника):

L=μN2Sl=μn2V.{\displaystyle \displaystyle L=\mu _{0}N^{2}S/l=\mu _{0}n^{2}V.}

Если катушка внутри полностью заполнена магнитным сердечником, то индуктивность отличается на множитель μ{\displaystyle \mu } — относительную магнитную проницаемость сердечника:

L=μμN2Sl=μμn2V.{\displaystyle \displaystyle L=\mu _{0}\mu N^{2}S/l=\mu _{0}\mu n^{2}V.}

В случае, когда μ>>1{\displaystyle \mu >>1}, под S

можно понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Фото собранного проекта от читателя нашего сайта

Читатель нашего сайта (его зовут Александр) собрал описанный в данной статье проект измерителя емкости и индуктивности на основе платы Arduino и решил поделиться с нами фотографиями собранного проекта, за что мы выражаем ему огромную признательность.

Здесь картинки представлены в сжатом виде (они кликабельны) в целях экономии интернет трафика, в оригинальном качестве вы можете скачать их с яндекс.диска или с гугл диска (ссылка в комментариях).

Применение катушек в технике

Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:

• сглаживание пульсаций и помех, накопление энергии;
• создание магнитных полей в различных устройствах;
• фильтры цепей обратной связи;
• создание колебательных контуров;
• трансформаторы (устройство из двух катушек, связанных индуктивно);
• силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
• ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
• применение катушек в качестве электромагнитов различных исполнительных механизмов;
• обмотки электромагнитных реле;
• индукционные печи;
• установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.

Работа на постоянном и переменном токе

Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:

B= µ0nI,

где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.

Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:

E = LI2 :2,

где L показывает значение индуктивности, а E – запасающую энергию.

ЭДС самоиндукции возникает при изменении тока в соленоиде.

В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.

Самое распространенное применение соленоидов первого типа (постоянного тока) — это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.

Логи

Я долго бился над тем, как записывать происходящее внтри микроконтроллера, ведь памяти у него совсем немного. В итоге я обнаружил, что родной SPI интерфейс очень быстрый, и в итоге вся отладочная информация передаётся микроконтроллером по интерфейсу SPI, для её записи был применён широкодоступный ($10 на дилэкстриме, $6 на алиэкспрессе) китайский клон логического анализатора Saelae Pro 8 Logic. После совсем нетрудных манипуляций по перепрошивке VID/PID, он может быть использован с родным софтом от Saelae. Я пользуюсь sigrok (pulseview). У него исключительно простой формат лог-файлов, которые я просто читаю своей самописной программкой в пятьдесят строк. Я купил этот анализатор по совету gbg, который мне дистанционно чинил мой спектрум (спасибо тебе огромное!), и считаю это самым выгодным вложением денег за последние два года.
Например, я подал синусоидальный сигнал (в ШИМ) на выход контроллера, и логический анализатор его прекрасно видит:

Всё это было соединено вместе, фотография дана в заголовке поста.

Практически все статьи, что я размещаю здесь, являются моим рабочим дневником. Я чему-то учусь (в данном случае теории управления) и старательно записываю то, что узнал. Лучший способ записать — это написать объяснение того, как это всё работает. Затем статьи выкладываю на разных площадках, например тут.

Целей при написании текста у меня две:

а) получить обратную связь от людей, которые знают больше меня.

Например, практически всё, что я узнал для данных двух статей, мне рассказал уважаемый Arastas, прошу любить и жаловать: человек, который тратит личное время на обучение таких оболтусов, как я.

Опять же, gbg, который написал мне линейную алгебру для моих лекций по компьютерной графике, а потом за много тысяч километров по телефону дебажил мне электронику.

б) просто записать:

таким образом я получаю библиотеку личного опыта, к которой периодически возвращаюсь.
Кстати, тематические медиа, какой процент авторов соглашаются на ваши условия программы поддержки?

Преобразование Фурье

Первое, что нужно понять, читая мои тексты: я считаю, что функция и вектор — это одно и то же. Все разговоры про бесконечности на меня навевают скуку и заслоняют суть происходящего. Обобщённые функции и тому подобное — это способ рассмотреть патологические случаи используя тот же самый язык, что и случаи, где никаких патологий нет. Вот только патологии меня не интересуют.
На эту тему хорошо высказался Валерий Иванович Опойцев (Босс):

В любой области полезно оказаться в подходящей среде устного общения, где осыпается книжная шелуха. Там иногда ничего не меняется по сути, зато возникает чувство попадания в колею и освобождения от догм. Для науки, которая всегда в маске, это особенно важно. Суть за кадром, перед глазами — кружева. И вечно чего-то не хватает. То простоты, то сложности, да точно и не определишь — чего. Что-то куда-то шагает, ты — на обочине, а время уходит в песок, не говоря о жизни.
Далее предпринимается попытка сдвинуть ситуацию с места, моделируя письменную среду, где «спадают покровы». Внешняя канва содержания более-менее неясна из оглавления, но главная цель — та, что за кадром. Снять вуаль, грим, убрать декорации. Переупростить, даже приврать слегка, ибо дозирование правды — краеугольный камень объяснения. Результаты, перегруженные деталями, не пролезают куда надо. Озарение случается, когда пухнущая голова проваливается на уровень «дважды два», в то время как счет идет на миллионы. Такая уж тут диалектика.

Если у нас есть вектор (7,12,18,-2), то его можно рассматривать как набор коэффициентов во взвешенной сумме. 7*(1,0,0,0) + 12*(0,1,0,0) + 18*(0,0,1,0) + (-2)*(0,0,0,1). Ровно так же можно считать этот вектор значениями функции в точках 0, 1, 2, 3, ведь наши векторы (0,1,0,0) и ему подобные можно рассматривать как сдвиг единичного импульса: Если постоянно увеличивать количество векторов (сдвинутых единичных импуьсов) в базисе, то получим обычные функции.
К сожалению, с таким базисом бывает довольно неудобно работать. Давайте рассмотрим следующую функцию в качестве примера:

Мы уже беседовали о том, что такое преобразование Фурье. Если кратко, то это смена базиса.

В нашем случае преобразование Фурье — это функция из вещественных чисел в комплексные:

Аргумент функции (вещественное число) — это просто номер базисной функции или вектора (на самом деле, пары базисных функций), а её значение — это соответствующая (пара) координат в для этих двух векторов в базисе. Базис Фурье — это синусы и косинусы различных частот. Частота и является номером базисной функции.

Для нашей конкретной функции f(t), которая уже являетя взвешенной суммой синуса и косинуса, очень легко посчитать её разложение в базис Фурье:

То есть, наша функция f(t) имеет нулевые координаты для всех векторов базиса, кроме векторов номер 11 и 41.

Чем полезен базис Фурье? Например тем, что операция дифференцирования линейно преобразует этот базис. Допустим, мы хотим посчитать преобразование Фурье от производной f'(t). Как это сделать? Как вариант, в лоб: сначала посчитать производную, а затем посчитать преобразование Фурье:

Очевидно, что при дифференцировании sin(x) он станет sin(x+90°), то есть крайне легко найти соответствие разложение в базис Фурье исходной функции и её производной: Умножение на
i
— это просто поворот комплексной плоскости, который соответствует +90° в аргументе нашей функции. То есть, операция дифференцирования, которую сложно делать в базисе единичных импульсов, в базисе Фурье — это просто масштабирование и поворот на 90 градусов. Красиво, правда?

Преобразование Лапласа

Примерно та же самая история происходит и с преобразованием Лапласа. К сожалению, в отличие от базиса Фурье, базис Лапласа неортогонален, поэтому для интуитивного понимания чуточку более сложен. Ну да не суть. Лаплас пошёл немного дальше. Если у Фурье в базисе были только синусоиды, то у Лапласа в базисе синусоиды с экспоненциальным затуханием. Откуда он их взял? Это крайне, крайне полезно при решении линейных дифференциальных уравнений. Давайте подумаем, какая функция преобразуется сама в себя при дифференцировании? Экспонента. А при дифференцировании два раза? Синус. А их комбинации дают все возможные функции, которые могут появиться при решении (линейных) диффуров, что и использовал маркиз дё Лаплас.
Не будем вдаваться в подробности того, как выводятся эти свойства (лучше рассмотрите внимательно свойства базиса Фурье, он проще), давайте просто отметим следующие факты:

1. Преобразование Лапласа линейно:

2. Преобразование Лапласа производной — это аффинное действие над преобразованием самой функции: 3. Итак, если у нас есть двигатель постоянного тока, то протекающий ток I(t) и напряжение на клеммах U(t) связаны следующим дифференциальным уравнением, где w(t) — это скорость вращения вала двигателя: Здесь L — это индуктивность, а R — сопротивление, которые мы и ищем. Я не буду повторять, откуда вылезает этот диффур, так как уже подробно и на пальцах его расписывал (см. «уравнения Максвелла на пальцах»).

Поскольку наша задача найти L и R, давайте жёстко зафиксируем вал двигателя, таким образом заставив w(t) быть нулевой:

По совету Arastas я подал два типа сигналов на мой двигатель: меандр и синусоиду. Затем я измерил протекающий ток, картинка получается примерно следующая:

Здесь синие кривые — это входное напряжение, котороя я контролирую, а зелёные — это измерения силы тока, полученные при помощи ACS714.

Мой микроконтроллерный код, который генерирует 11 экспериментов с меандром и синусоидами различных амплитуд и частот, можно посмотреть здесь.

Давайте решим наше дифференциальное уравнение для обоих типов сигнала напряжения, получим параметрический выходной сигнал силы тока, и подберём параметры, чтобы теоретическая кривая как можно лучше аппроксимировала реальные измерения.

Входной сигнал — синус

Повторим процедуру для синусоиды напряжения с амплитудой U0 и частотой F0. Применим преобразование Лапласа к уравнению (1), сначала к правой части: а потом и к левой: Теперь обратное преобразование нам даст следующий закон протекания тока: Опять быстрый sanity check: нулевой ток в самом начале, несколько миллисекунд переходных процессов (экспонента, напрямую зависящая от индуктивности). По истечению некоторого времени протекающий ток — это взвешенная сумма синуса и косинуса одной и той же частоты (частота равна входной, это хорошо). Эта сумма даёт синусоиду, чуть сдвинутую во времени. Отлично, результат правдоподобен.
Измерения лежат здесь, а код подбора параметров тут. Он даёт примерно такие же значения сопротивления и индуктивности, что нам и требовалось. Вот график:

Почему не измерить параметры напрямую, зачем весь этот огород с микроконтроллерами? Во-первых, мне нечем измерять индуктивность. Да и измерение сопротивления двигателя омметром может иметь свои нюансы.

Далее, параметры, найденные при высокой амплитуде сигнала, не совсем совпадают с тем, что получается при низких напряжениях. Может быть интересно (тут не рассмотрено) делать модель не только двигателя, а всей системы в целом, включая нелинейность ШИМ-драйвера.

Ну а дальше осталось разработать регулятор, который будет на вход брать необходимую силу тока. Оставайтесь на связи!

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

• L — индуктивность контура (в генри);
• Ф — величина магнитного потока, измеряемого в веберах;
• I — сила тока в катушке (в амперах).

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

• µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
• N — количество витков в катушке;
• S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
• l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

• W — энергия магнитного потока, измеряемая в джоулях;
• I — сила тока в амперах.

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

• N — число витков катушки;
• µ — относительная магнитная проницаемость;
• µ0 — магнитная постоянная;
• S — площадь сечения сердечника;
• π — математическая постоянная, равная 3,14;
• r — средний радиус тора.

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

• l — длина проводника в метрах;
• r — радиус сечения провода, измеряемый в метрах;
• µ0 — магнитная постоянная;
• µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
• µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
• π — число Пи;
• ln — обозначение логарифма.

Добротность катушки

Одно из важнейших качеств катушек – это добротность. Данный параметр представляет собой отношение реактивного (индуктивного) сопротивления к активному. Активное сопротивление – это сопротивление проводника, из которого выполнен элемент, его можно считать постоянным, за исключением температурного коэффициента сопротивления материала, из которого выполнен провод.

Реактивное сопротивление прямо пропорционально частоте. Формула расчета добротности выглядит следующим образом:

где:

• π – число пи, ≈3,14,
• f – частота,
• R – сопротивление.

Обратите внимание! С ростом частоты сигнала добротность катушки индуктивности возрастает

Аналоговый мультиметр

Данный тип мультеметров отображает показания измерений при помощи стрелки, под которой установлено табло с различными шкалами значений. Каждая шкала отображает показания того или иного измерения, которые подписаны непосредственно на табло.

Но для новичков такой мультиметр будет не самым лучшим выбором, поскольку разобраться во всех обозначениях, которые находятся на табло довольно трудно. Это может привести к не правильному пониманию результатов измерения.

Бизнес и финансы

Бизнес
: • Банки • Богатство и благосостояние • Коррупция • (Преступность) • Маркетинг • Менеджмент • Инвестиции • Ценные бумаги: • Управление • Открытые акционерные общества • Проекты • Документы • Ценные бумаги — контроль • Ценные бумаги — оценки • Облигации • Долги • Валюта • Недвижимость • (Аренда) • Профессии • Работа • Торговля • Услуги • Финансы • Страхование • Бюджет • Финансовые услуги • Кредиты • Компании • Государственные предприятия • Экономика • Макроэкономика • Микроэкономика • Налоги • Аудит
Промышленность
: • Металлургия • Нефть • Сельское хозяйство • Энергетика
Строительство
• Архитектура • Интерьер • Полы и перекрытия • Процесс строительства • Строительные материалы • Теплоизоляция • Экстерьер • Организация и управление производством

Фотоблоги

Искусство

• Детское творчество • Картины • Искусство • Поздравления • Кинобзор • Музыкальный мир • Русский рок

Мир

• Люди мира • Мир вокруг нас • Моя родина — СССР • Канал «Природа» • Камни и минералы • Кулинария, еда • Строительство и архитектура • Строимся • Транспорт • Оружие • Военный транспорт

Красота

• Fashion Pandia.ru • Girls and Girls

Школа

• Тесты к ЕГЭ • Решебники • ЕГЭ • 10 и 11 классы • Разные учебники • 4 класс • Русский язык 5-9 классы • 5 класс • 6 класс • 7 класс • 8 класс

Мудрость

• Клипарты • Цитаты

Каталог авторов (частные аккаунты)

Авто Автосервис • Автозапчасти • Товары для авто • Автотехцентры • Автоаксессуары • автозапчасти для иномарок • Кузовной ремонт • Авторемонт и техобслуживание • Ремонт ходовой части автомобиля • Автохимия • масла • техцентры • Ремонт бензиновых двигателей • ремонт автоэлектрики • ремонт АКПП • Шиномонтаж Бизнес Автоматизация бизнес-процессов • Интернет-магазины • Строительство • Телефонная связь • Оптовые компании Досуг Досуг • Развлечения • Творчество • Общественное питание • Рестораны • Бары • Кафе • Кофейни • Ночные клубы • Литература Технологии Автоматизация производственных процессов • Интернет • Интернет-провайдеры • Связь • Информационные технологии • IT-компании • WEB-студии • Продвижение web-сайтов • Продажа программного обеспечения • Коммутационное оборудование • IP-телефония

Инфраструктура Город • Власть • Администрации районов • Суды • Коммунальные услуги • Подростковые клубы • Общественные организации • Городские информационные сайты Наука Педагогика • Образование • Школы • Обучение • Учителя Товары Торговые компании • Торгово-сервисные компании • Мобильные телефоны • Аксессуары к мобильным телефонам • Навигационное оборудование