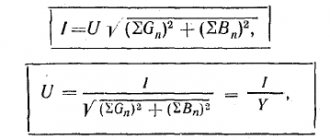В общих физических понятиях условия резонанса возникают при совпадении частоты внешних воздействий с внутренними параметрами системы. Наглядный пример – качание маятника. При правильном подборе движений слабым усилием существенно увеличивают амплитуду колебаний. Аналогичный результат можно получить в электрических цепях, которые составлены из компонентов с реактивными характеристиками.
Определение резонанса
Использование резонанса напряжений для передачи радиосигнала
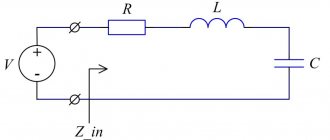
Колебательный контур этого типа создают из последовательной комбинации трех базовых компонентов: резистор, конденсатор, индуктивность. Подходящим для резонанса условием является нулевое сопротивление цепи (комплексное). Для решения такой задачи следует изучить основные формулы.
Комплексное сопротивление Rк=R+j(wL-1/wC). Постоянный резистор (R) не зависит от частоты (w). Значит, придется оперировать с индукционными и емкостными элементами. Резонансный эффект получают при (wL-1/wC)=0. Для вычисления необходимых значений пользуются следующими расчетами:
- Lп=1/w2*C;
- Сп=1/w2*L;
- Wп=1/√L*C.
Из приведенных данных понятно, что корректировать можно любой из параметров при одновременном сохранении двух других. В практической схемотехнике удобнее работать с частотой, поэтому рассмотрим подробнее применение такого варианта.
Последовательный контур с графиками
На рисунках показаны условия возникновения резонанса напряжений. В точке, обозначенной w0, наблюдается равенство индуктивной и емкостной составляющих на определенной частоте. Небольшой сдвиг влево по оси обусловлен резистивным компонентом цепи.
Напряжение на конденсаторе (Uc) при частоте резонанса (W0) равно волновому сопротивлению колебательного контура (p=√L/C). Аналогичная разница потенциалов будет на клеммах катушки при частоте W0. Данная особенность объясняет особое название процесса – «резонанс напряжений». Также в электротехнических расчетах применяют следующие определения:
- Добротность – Q=p/R;
- Затухание – 1/Q.
Отмеченные свойства используют в радиоприемной и передающей аппаратуре. Выделение контуром определенного диапазона позволяет выполнять настройку станции на определенную частоту с определенной параметрами цепи погрешностью. Для контроля избирательности оценивают амплитуду сигнала относительно резонансной частоты. Уровень отклонения на 3 дБ в обе стороны (0,7 от максимума) называют полосой пропускания.
Амплитудно-частотная характеристика (АЧХ) и полоса пропускания
Примеры применения на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.
Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.
Катушки индуктивности
Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Наряду с полезными свойствами резонансных явлений, в практической электротехнике часто возникают ситуации, когда резонанс напряжений приносит вред. В основном это связано с нежелательным повышением параметров тока на участках цепей. Примером могут служить опасное резонансные явления в кабельных линиях без нагрузки, что может привести к пробоям изоляции. Чтобы этого не случилось, на концевых участках таких линий устанавливают балластные нагрузочные элементы.
Собственная частота резонансного контура
Мощность резистора
Емкость конденсатора (С) в совокупности с индуктивностью катушки (L) определяют собственную частоту контура (Wc). Для приблизительных расчетов пользуются формулой Wc=1/√L*C. В этом случае речь идет об идеальных условиях, когда потерями пренебрегают по причине минимальных значений.
Для повышения точности применяют коэффициент затухания (Кз). С учетом этого фактора можно привести следующую зависимость между собственной и резонансной частотами:
Wo=√Wc2-2*Кз2.
Резонатор Гельмгольца
Удивительные свойства пустых сосудов человечество знает давно. Античные архитекторы при строительстве театра использовали знания о звуковом резонансе: закладывали в стены сосуды из бронзы, чтобы голос актеров звучал громче. В акустике широко применяются резонаторы Гельмгольца. Гельмгольц — это немецкий ученый, который обосновал теорию слуха с физической точки зрения. С помощью набора резонаторов, названных в его честь, можно анализировать сложные звуки по частоте колебаний волны.
Как же работает резонатор? Он представляет собой шарообразный или в форме бутылки сосуд с узким горлышком. Весь секрет состоит в звуковом резонансе колебаний воздуха, который находится внутри. Звуковая волна сложная. Она состоит из множества колебаний. Но каждый из резонаторов лучше всего отзывается на ту частоту, которая равна его собственной, т. е. частоту колебания воздуха, заключенного в полости. От чего она зависит?
Если резонатор меньше длины звуковой волны, то его принцип действия такой же, как у пружинного маятника. Воздух в узком горлышке движется намного быстрее, чем в самом резонаторе. Именно колебания в горлышке сосуда играют главную роль. Получается, что кинетическая энергия сосредоточена преимущественно в этом узком месте. Упругую энергию несет масса воздуха, находящаяся внутри резонатора.
Воздуха в горлышке гораздо меньше, чем внутри, поэтому изменением его объема во время колебаний принято пренебрегать. Условно считается, что вся эта масса передвигается как единое целое, как воздушная пробка, а объем воздуха внутри резонатора меняется сильно. Получается, что воздух внутри работает как пружина в колебательной системе. Его приток перекрывает путь в сосуд другому воздуху, а отток понижает давление и препятствует выпусканию воздуха изнутри. Когда воздушная пробка идет вниз, она сжимает близлежащий слой воздуха внутри резонатора, т. е. повышает его плотность. В результате растущее давление приводит в движение следующий слой воздуха, потом еще один и т. д. Таким образом, сжатие распространяется по слоям, передает свой импульс, и возникает звуковая волна.
Теперь понятно, что причиной жутких голосов в доходном доме был звуковой резонанс. Вой ветра и другие шумы с улицы — это неупорядоченные гармонические колебания разной частоты. Их называют чистыми тонами. При прохождении через стену все частоты, кроме резонансных, слабели. Резонансные частоты — это те, что совпадали с частотами воздуха в пустых сосудах. Более того, они могли даже усилиться. Городовые впадали в панику, потому что слышали несвойственные человеку и живым существам звуки. Дело в том, что наша речь звучит на частоте, гораздо большей 100 герц, а «домовой» издавал необычно низкие звуки.
Резонанс токов, параллельный резонанс
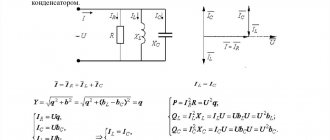
В электротехнике часто применяют не последовательное, а параллельное соединение конденсатора и катушки.
Следует помнить! В такой ситуации реактивные элементы рассматривают по измененной схеме. Вместо сопротивлений оперируют суммой проводимостей.
Электрические параметры и компоненты, векторные диаграммы напряжений и токов
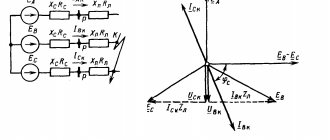
В этом примере рассмотрим уточненные параметры. Величину (I) определяют по сумме токов, которые проходят по индуктивному и емкостному участкам цепи. В обеих ситуациях определенное значение имеет частота (w):
- IL=E/(RL+Кз*w*L);
- Ic=E/(Rc+(1/Кз*w*С).
Диаграммы наглядно демонстрируют характерные изменения физических параметров при работе контура в трех типовых режимах. На рисунке а) изображен емкостной вариант. Предполагается что w*L больше, чем 1/w*С. В этом случае минимальным значением RL можно пренебречь, что несколько упрощает приведенную выше формулу для расчета тока. Он будет отставать от вектора напряжения на угол ϕL. Второй рисунок демонстрирует обратную ситуацию, когда IL больше Ic.
Для резонансных условий надо, чтобы фазы совпадали. Это показано векторами на рисунке в). Такая ситуация получится, если w*L равно 1/ w*С. В этом случае наблюдается примерное равенство IL и Ic, что определено во втором названии явления – «резонанс токов».
Описание явления
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.
Рис. 1. Резонанс в электрической цепи
Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).
Рис. 2. Графики зависимости параметров тока от падения реактивного сопротивления
Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).
Рис. 3. Последовательный колебательный контур
Рис. 4. Параллельный колебательный контур
В режиме резонанса мощность источника питания будет рассеиваться только на активных сопротивлениях (в том числе на активном сопротивлении катушки). Для резонансных контуров характерны потери только активной мощности, которая израсходуется на поддержание колебательного процесса. Реактивная мощность на L C — элементах при этом не расходуется. Ток в резонансном режиме принимает максимальное значение:
Величину Q принято называть термином «Добротность контура». Данный параметр показывает, во сколько раз напряжение, возникшее на контактах реактивных элементов, превышает входное напряжение U электрической сети. Для описания соотношения выходного и входного напряжений часто применяют коэффициент K. При резонансе:
K = Uвых / Uвх = UC0 / U = Q
На основании вышеописанных явлений, сформулируем определение резонансного напряжения: «Если общее падение напряжения на ёмкостно-индуктивных элементах равно нулю, а амплитуда тока – максимальна, то такое особое состояние системы называется резонансом напряжений». Для лучшего понимания явления, немного перефразируем определение: резонансом напряжений является состояние, когда напряжение на CL — цепочке больше чем на входе электрической цепи.
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
В случае, если XL = Xc – справедливо равенство: ωL = 1/ωC , отсюда получаем:
Если ω = ω0 – возникает резонанс напряжений. Частоты совпадают в том случае, когда индуктивное сопротивление сравняется с ёмкостным сопротивлением конденсатора. В таких случаях в цепи будет действовать только активное сопротивление R. Наличие реактивных элементов в схеме приводит к увеличению полного сопротивления цепи (Z):
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Будет интересно➡ Особенности резонанса токов
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Резонанс в распределённых колебательных системах, нелинейные процессы
Общим понятием для всех явлений данной категории можно назвать действенную связь с окружающей средой. В механических системах влияние на амплитуду фазовых характеристик процесса оказывает определенное положение в пространстве. В колебательном контуре радиоприемника, кроме собственного затухания, приходится учитывать реальный электромагнитный фон. При определенных условиях с высоким значением добротности допустимо образование стоячих волн.
Следует понимать! Результат воздействия во многом зависит от совпадения по фазе и частоте.
Если пружина создана с различным распределением плотности витков, типовые формулы не действуют. Стандартные расчеты подразумевают равномерные упругость и деформации каждой части. Для уточнения нелинейности применяют корректирующие коэффициенты, сложные многоэтапные схемы вычислений.
Аналогичные особенности учитывают при использовании диодов или других радиотехнических компонентов с переменными амплитудно-частотными характеристиками. Если катушку индуктивности намотать на сердечнике из ферромагнитного материала, также придется учитывать нелинейность выходных параметров. Ее не получится описать элементарным уравнением закона Ома.
В нелинейных контурах при определенном спектральном распределении внешних воздействий присутствуют гармонические колебания. Кроме совпадения частот, значение имеет их амплитуда. В зависимости от настроек, они способны выполнять полезные и вредные функции. Определенные условия вызывают искажение формы базового сигнала.
«Поющий» камень
Недалеко от Баку, столицы Азербайджана, есть пустыня со знаменитым «поющим» камнем. Он настолько известен, что получил имя — «Каменный бубен». Эта удивительная глыба имеет свойство: если ударить по ней камнем, то звук получается такой же громкий и чистый, как у колокола. Как же физика объясняет этот пример звукового резонанса?
Удар приводит к краткосрочной деформации — тут же от точки столкновения во все стороны бегут звуковые волны. На скорость их расхождения размеры камня не влияют. Однако волна может свободно распространяться только в неограниченном пространстве. А ведь мы знаем, что камень и воздух имеют границы (там, где они соприкасаются).
Резонанс в линейных системах с одной степенью свободы
К этой группе можно причислить рассмотренные последовательные и параллельные электрические схемы. Механический пример – пружина с грузом, который способен перемещаться только по вертикальной прямой. Исключены порывы ветра, вибрации, другие «паразитные» внешние воздействия. В подобных условиях можно применять типовые формулы для систем линейного типа.
Отмеченная выше добротность является определяющим фактором для избирательности по частоте. Сужение ширины резонансного диапазона помогает улучшить характеристики приемных и передающих устройств. Кроме экономного расходования электроэнергии, при правильном расчете схемы существенно улучшается помехозащищенность.
Таинственный дом
В «Рассказах о старой Москве» А. Вьюркова описывается звучащий страшным голосом дом. Главный герой произведения Иван Павлович решил разбогатеть обманным путем. Он нанял бригаду каменщиков, чтобы те построили ему доходный дом, и не заплатил им всей обещанной суммы. Вскоре арендаторы стали один за другим покидать гостиницу, потому что были напуганы нечистой силой, которая выла нечеловеческим голосом.
Иван Павлович остался без денег и без жильцов. Ему нечем было выплачивать проценты по кредиту, поэтому имущество и его самого арестовали. По прошествии времени один из подрядчиков раскрыл Ивану Павловичу секрет мистического дома. Оказывается, что обманутые рабочие решили отомстить: они замуровали в стену пустые бутылки, которые звучали при каждом порыве ветра, пугая постояльцев.
Параллельный резонанс при источнике ЭДС
Добротность для параллельной схемы вычисляют по формуле Q=R√C/L. При равенстве частот (источника и контура) сопротивление в отдельных ветвях не различается. Одинаковые значения токов создают компенсированные реактивные параметры конденсатора и катушки.
При отклонении частоты от резонансного значения в нижний (верхний) диапазон сопротивление приобретает емкостной (индуктивный) характер, соответственно. В обычном рабочем цикле происходит энергетический обмен между реактивными элементами цепи. Этот режим характеризуется увеличением в Q раз тока, проходящего по внутреннему контуру, по сравнению с поступающим от источника ЭДС. Идеальные условия, когда добротность стремится к бесконечной величине, невозможны. Прямые и паразитные потери в цепях ограничивают рост силы резонансного тока.
Механические колебания маятника
Самая простая модель, которая может наглядно показать колебания, это простейший маятник, а точнее математический маятник. Колебания разделяют на свободные и вынужденные. Первоначально воздействующая энергия на маятник обеспечивает в теле свободные колебания без присутствия внешнего источника переменной энергии воздействия. Данная энергия может быть как кинетической, так и потенциальной.
Здесь не имеет значение насколько сильно или нет качается сам маятник, — время, потраченное на прохождения его пути в прямом и обратном направлении, сохраняется неизменным. Во избежание недоразумений с затуханием колебаний вследствие трения о воздух стоит выделить, что для свободных колебаний должны соблюдаться условия возврата маятника в точку равновесия и отсутствия трения.
А вот частота в свою очередь напрямую зависит от величины длины нити маятника. Чем короче нить, тем выше частота и наоборот.
Возникающая естественная частота тела под воздействием первоначально приложенной силы называется резонансной частотой.
Все тела, которым свойственны колебания, совершают их с заданной частотой. Для поддержания в теле незатухающих колебаний необходимо обеспечить постоянную периодическую энергетическую «подпитку». Это достигается воздействием в одновременный такт колебаний тела постоянной силы с определенным периодом. Таким образом возникающие колебания в теле под действием периодической силы снаружи называют вынужденными.
В какой-то момент внешних воздействий возникает резкий скачок амплитуды. Такой эффект возникает если периоды внутренних колебаний тела совпадают с периодами внешней силы и называется резонансом. Для возникновения резонанса достаточно совсем небольших величин внешних источников воздействия, но с обязательным условием повторения в такт. Естественно, при фактических расчетах в земных условиях не стоит забывать о действии сил трения и сопротивления воздуха на поверхность тело.
Последовательный резонанс при источнике тока
Измерение сопротивления в цепи с последовательно подключенными реактивными элементами поможет фиксировать на определенной частоте резонанс. В этом случае для эксперимента пользуются источником тока. При низкой (высокой) частоте ограничивающее влияние оказывают емкостные (индуктивные) характеристики цепи. На частоте резонанса суммарное реактивное сопротивление минимально.
Электрические параметры в последовательном контуре
На рисунках изображены следующие зависимости от частоты:
- а. общего сопротивления;
- б. реактивных компонентов;
- в. силы тока в резонансных режимах.
См. также
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Ёмкость в линии с током постоянной величины выглядит как разомкнутый отрезок цепи, индукция представлена проводником. При переменном токе реактивный резисторный аналог представлен катушками с устройствами конденсации.
Реактивная сопротивляемость зависима от значения ёмкости либо индуктивности, а также частоты тока с переменной величиной.
Глядя на расчёт реактивного значения, становится заметно, что имея определённые значения индуктивного либо ёмкостного элемента, разность их равняется нулю, и, как следствие, в остатке будет находиться активное сопротивление. У этой ситуации есть ещё некоторые нюансы.
Резонанс в реальных цепях
Для изучения описанных процессов надо собрать контур из соответствующих компонентов. Придется подготовить генератор с изменяющейся частотой выходного сигнала, осциллограф и другие измерительные инструменты. Чтобы получить достоверные результаты без лишних трудностей, пользуются специализированным программным обеспечением.
Теория и практика
В левой части рисунка размещены схема и амплитуда сигнала на выходе при подключении к выводам конденсатора параллельного контура. В правой – снимок экрана измерительной аппаратуры. Несложно убедиться в идентичности колебаний.
К сведению. С помощью ПО выполняют десятки экспериментов быстро и точно в обычных домашних условиях. Этот способ значительно упрощает создание электрических схем с оптимальными параметрами.
Реактивные сопротивления индуктивности и емкости
Индуктивностью называется способность тела накапливать энергию в магнитном поле. Для нее характерно отставание тока от напряжения по фазе. Характерные индуктивные элементы — дросселя, катушки, трансформаторы, электродвигатели.
Емкостью называются элементы, которые накапливают энергию с помощью электрического поля. Для емкостных элементов характерно отставание по фазе напряжения от тока. Емкостные элементы: конденсаторы, варикапы.
Приведены их основные свойства, нюансы в пределах этой статьи во внимание не берутся.
Кроме перечисленных элементов другие также имеют определенную индуктивность и емкость, например в электрических кабелях распределенные по его длине.
Резонанс в линейных колебательных системах с несколькими степенями свободы
Такие расчеты понадобятся при конструировании двух последовательных контуров с индуктивной связью. В этом случае переменные колебательные процессы оказывают взаимное влияние. Фактически речь идет о распределенной системе.
Кроме схемотехники, в подобных ситуациях отдельно изучают коэффициент связи (Кс). При работе с трансформатором его вычисляют делением напряжений на первичной (вторичной) катушке, соответственно. Следует учесть реактивные характеристики, которые преобладают в рабочем диапазоне частот.
Узнав, что такое резонанс напряжений и токов, можно самостоятельно реализовать различные проекты. Тщательная предварительная подготовка необходима для создания схемы с хорошими эксплуатационными параметрами. Начинают с чертежей и расчетной части. Теоретические изыскания дополняют изготовлением макета и практическими испытаниями. Ускоряют подготовку конструкторской документации, а также выполняют эксперименты с применением программного обеспечения. В наиболее сложных ситуациях обращаются к опытным специалистам.
Как используется
Резонансные токи используются сегодня в некоторых фильтрующих системах, радиотехнике, электричестве, радиостанциях, асинхронных двигателях, высокоточных электрических сварных установках, колебательных генераторных электрических контурах и высокочастотных приборах. Нередко, когда они применяются, чтобы снизить генераторную нагрузку.
Обратите внимание! Простейшая цепь, где наблюдаются они, это параллельного вида колебательный контур. Такие контуры используются в современном промышленном индукционном котловом оборудовании и улучшают показатели КПД
Сфера применения
Опыт с камертонами
Акустическая волна подобна качелям: если толкать их как попало, сбиваясь с ритма, то высоко она не взлетит
Важность совпадения частоты (ритма) легко можно увидеть в эксперименте с двумя камертонами. Возьмем те, что имеют одинаковую частоту, и поставим довольно близко друг от друга
Ударим молоточком по ножкам первого — он зазвучит, и очень скоро заставит звучать другой. Почему это произойдет? Второй инструмент будет приведен в движение (раскачан) звуковой волной. Когда первый замолчит, второй будет издавать звук еще некоторое время. Вот как возникает звуковой резонанс. Если проделать опыт на камертонах разной частоты, мы увидим, что они не резонируют.