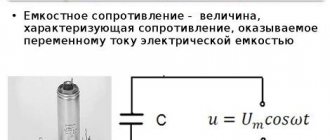
Реактивное сопротивление катушки индуктивности
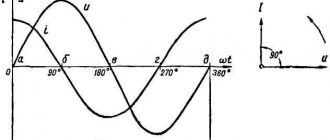
При протекании переменного тока I
в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока. При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U
, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U
, ток не может начаться мгновенно по причине противодействия ЭДС, равного
-U
, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u
исходя из ЭДС (
ε
), которая пропорциональна индуктивности
L
и скорости изменения тока:
u = -ε = L(di/dt)
. Отсюда выразим синусоидальный ток .
Интегралом функции sin(t)
будет
-соs(t)
, либо равная ей функция
sin(t-π/2)
. Дифференциал
dt
функции
sin(ωt)
выйдет из под знака интеграла множителем 1
/ω
. В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол
π/2
(90°). Для среднеквадратичных значений
U
и
I
в таком случае можно записать .
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R
выражение
ωL
, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
§ 59. Понятие о резонансе напряжений
В цепи переменного тока с активным, индуктивным и емкостным сопротивлениями, соединенными последовательно (рис. 62, а), может возникнуть резонанс напряжений.
При резонансе напряжения на зажимах индуктивного и емкостного сопротивлений могут стать значительно больше, чем напряжение на зажимах цепи. Резонанс напряжений наступает в том случае, если индуктивное сопротивление XL
и емкостное сопротивление
Xc
равны между собой, т. е.
Допустим, что подбором индуктивиости и емкости или изменением частоты создано условие, при котором XL
=
Xc
Когда цепь не настроена в резонанс, то ее полное сопротивление
а в рассматриваемой цепи при резонансе (когда XL
=
Xc
) ее полное сопротивление
Таким образом, полное сопротивление цепи при резонансе оказывается равным активному сопротивлению. Уменьшение полного сопротивления цепи приводит к тому, что сила тока в ней возрастает. Напряжение генератора переменного тока, включенного в цепь, расходуется на активном сопротивлении
Ua = I r
.
Напряжение на индуктивности определяется, согласно закону Ома, произведением силы тока на величину индуктивного сопротивления. Так как в цепи увеличилась сила тока, то напряжение UL = I XL
возросло. Напряжение на емкости также определяется произведением тока на величину емкостного сопротивления. Поэтому напряжение на емкости
Uc = I Xc
. В связи с тем, что в последовательно соединенных сопротивлениях протекает одинаковый ток и при резонансе индуктивное сопротивление
XL
равно емкостному сопротивлению
Хс
, напряжение на индуктивности и напряжение на емкости равны:
UL = Uc
или
I XL = I Xc
Если одновременно увеличить оба реактивных сопротивления ХL
и
Хc
, не нарушая при этом условия резонанса
ХL
=
Хc
, то соответственно возрастут оба частичных напряжения
UL
и
Xc
, а сила тока в цепи при этом не изменится. Таким путем можно получить
UL
и
Uc
во много раз большие, чем напряжение
U
на зажимах цепи. Построим векторную диаграмму (рис. 62, б) для рассматриваемой цепи при резонансе напряжения. Отложим по горизонтали в выбранном масштабе вектор тока . В активном сопротивлении ток и напряжение совпадают по фазе. Поэтому вектор напряжения отложим по вектору тока. Так как напряжение на индуктивности опережает ток на 90°, то вектор отложим вверх под углом 90°. Напряжение на емкости отстает от тока на 90°, поэтому вектор , равный вектору , отложим вниз под углом 90° к вектору тока. На векторной диаграмме видно, что напряжение на индуктивности и напряжение на емкости равны и сдвинуты по фазе друг относительно друга на 180° и взаимно компенсируются. Угол сдвига фаз между током и напряжением при резонансе равен нулю. Это значит, что ток и напряжение совпадают по фазе (как в цепи с активным сопротивлением).
Пример.
В цепь переменного тока включены последовательно активное сопротивление
r
= 5
ом
, индуктивность
L
= 0,005
гн
и емкость 63,5
мкф
. Генератор, включенный в цепь, вырабатывает переменное напряжение
U
= 2,5
в
с резонансной частотой
f
= 285
гц
. Определить индуктивное и емкостное сопротивления, полное сопротивление цепи, ток, протекающий в цепи, напряжение на емкости и на индуктивности. Решение. Индуктивное сопротивление
XL = 2πf L
= 2 · 3,14 · 285 · 0,005 = 8,9
ом
,
Емкостное сопротивление
Индуктивное сопротивление равно емкостному сопротивлению и, следовательно, в цепи наступает резонанс напряжения. Полное сопротивление цепи при резонансе
Сила тока в цепи
Напряжение на индуктивности
UL = I XL
= 0,38 · 8,9 = 7,4
в
Напряжение на емкости
Uc = I Xc
= 0,38 · 8,9 = 7,4
в
Как видно из приведенного примера, напряжения на индуктивности и емкости равны и превышают напряжение генератора.
предыдущая страница
| оглавление | следующая страница |
Лекция для колледжа по электротехнике на тему «Резонанс в цепи переменного тока.»
Лекция 8.
Цепь с активным сопротивлением, индуктивностью и ёмкостью. Резонансный режим работы цепи. Резонанс напряжений. Резонанс токов. Коэффициент мощности.
Цепь с активным сопротивлением, индуктивностью и ёмкостью.
Цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий
случай последовательного соединения активных и реактивных сопротивлений и является
последовательным колебательным контуром.
Рис. а) Цепь с резистором, катушкой индуктивности и конденсатором, б) Векторная диаграмма цепи, в) треугольник сопротивлений цепи R,
XLи ХС
Принимаем фазу тока нулевой: i
=Imsin
* t ;
Тогда uR=
Umsin
* t;
uL=Umsin (
* t + /2);
uС=Umsin (
* t — /2)
Построим векторную диаграмму при ХL>ХС, то есть UL= I ХL> UC= I ХC
Вектор результирующего напряжения U замыкает многоугольник векторов UR, UL и UC. Вектор UL+UC определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процессом обмена энергией между индуктивностью и емкостью.
Так как модуль вектора UL+UC рассчитывают как разность действующих значений UL—UC, то
и поэтому
Закон Ома для этой цепи при этом ,
где Z – полное сопротивление цепи.
Разность между индуктивным и емкостным сопротивлениями XL—XC=X называют
реактивным сопротивлением цепи.
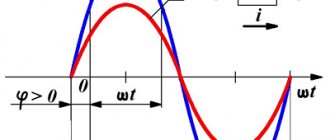
При XL>XС реактивное сопротивление положительно и сопротивление цепи носит активноиндуктивный характер. При этом угол сдвига фаз φ>0 положительный.
При XLC реактивное сопротивление отрицательно и сопротивление цепи носит активноемкостный характер. При этом угол сдвига фаз φ<0 отрицательный.
Резонансный режим работы цепи.
Резонансный режим работы – это режим при котором сопротивление является чисто активным. По отношению к источнику питания элементы цепи ведут себя в резонансном режиме как активное сопротивление, поэтому ток и напряжение в неразветвленной части совпадают по фазе. Реактивная мощность цепи при этом равна нулю.
Различают резонанс напряжений и резонанс токов.
Резонанс напряжений.
Резонанс напряжений происходит в цепи последовательного колебательного контура, когда ток в цепи совпадает с напряжением по фазе φ=0о.
а) б) с)
Рис. а) Последовательный резонансный контур, б) Векторная диаграмма цепи при XL=XC, в) резонансная кривая последовательного контура.
Реактивное сопротивление последовательного контура равно нулю Х=0
при
XL=XC.
Так как ХL
=
L
; Хс =1/
C ; =
2
f тогда
Резонансная частота При резонансе напряжений частота источника равна собственной частоте колебаний контура.
Условие резонанса напряжений:
а) сопротивление цепи Z = R
минимальное и чисто активное;
б) ток цепи совпадает по фазе с напряжением источника и достигает максимального значения;
в) напряжение на индуктивной катушке равно напряжению на конденсаторе и каждое в отдельности может во много раз превышать напряжение на зажимах цепи.
Величину называют волновым сопротивлением контура.
Резонансная кривая показывает зависимость действующего значения тока в контуре от частоты источника при неизменной собственной частоте контура.
Поместим зависимость индуктивного и ёмкостного сопротивлений от частоты источника на один график .
Рис. Зависимость реактивного сопротивления Х от частоты источника.
При частотах, близких к f
0, реактивное сопротивление мало и ток контура велик.
Резонанс напряжений широко используется в радиотехнике и электронике для выделения
сигналов заданной частоты.
Резонанс токов.
Резонанс токов происходит на неразветвлённом участке цепи параллельного колебательного контура, когда ток совпадает с напряжением по фазе φ=0о.
а) б)
Рис. а) Параллельный колебательный контур, б) Векторная диаграмма при резонансе токов.
Если IR будет мало, то Iс = ILР
Условие резонанса тока:
а) полное сопротивление контура Z максимально и полностью активно,
б) ток в неразветвлённой части цепи совпадает по фазе с напряжением и очень маленький,
в) реактивная составляющая тока в катушке равна реактивной составляющей тока в ёмкости.
Для того чтобы ток I
в неразветвленной части цепи совпадал по фазе с напряжением,
реактивная составляющая тока индуктивной ветви I
Lp должна быть равна по модулю току
емкостной ветви I
C . Активная составляющая тока индуктивной ветви
I
La оказывается
равной току источника I
. Определим сопротивление контура в предположении
R
<<
X
L.
Сформулируем признаки резонанса токов:
а) сопротивление контура Zк максимальное и чисто активное;
б) ток в неразветвленной части цепи совпадает по фазе с напряжением источника и
достигает практически минимального значения;
в) реактивная составляющая тока в катушке равна емкостному току, причем эти токи
могут во много раз превышать ток источника.
Коэффициент мощности.
По аналогии с треугольником сопротивлений для последовательного соединения резистора, катушки индуктивности и конденсатора можно получить треугольник напряжений и мощностей.
Рис. Треугольник сопротивлений и расчёт полного сопротивления
Рис. Треугольник мощностей и расчёт полной мощности
Активная мощность, развиваемая генератором в номинальном режиме P=Iном
Uномcosφ
Полное использование мощности генератора происходит при cos
φ = 1
. При этом активная мощность максимальна и равна номинальной полной мощности
Sном=IномUном
Реальная электрическая цепь переменного тока обязательно содержит реактивное сопротивление. Это увеличивает потери на нагрев.
Cos
φ называют коэффициентом мощности.
cos
φ =P/S–это отношение активной мощности к полной мощности.
Он показывает, какая часть электрической энергии, вырабатываемая источником переменного тока, используется на выполнение полезной работы.
Уменьшение cos
φ
приводит к увеличению тепловых потерь в линии передачи, которые растут обратно пропорционально квадрату коэффициента мощности. Для полного использования номинальной мощности генераторов и уменьшения тепловых потерь необходимо повышать
cosφ
приемников энергии до значений, близких к единице (0,95—1,0).
Для повышения cos
φ
параллельно приемнику энергии включают батареи конденсаторов.
Благодаря этому источником реактивной энергии для приемника становится емкость и линия
передачи разгружается от реактивного тока.
На практике к приемникам с удовлетворительным cos
φ
относятся в качестве промышленного привода асинхронные двигатели. Значение
cosφ
у них колеблется в пределах 0,1—0,3 при холостом ходе и 0,8—0,85 при номинальной нагрузке.
Векторные диаграммы цепи для xl xc
Построение векторной диаграммы
Для цепей последовательного соединения на диаграммах строят векторы:
1) Силы тока I — — он единственный, потому что токи через участки цепи равны
2) Напряжений (падений напряжений на участках) — их четыре по числу соединенных элементов.
Согласно теории на активном сопротивлении нет сдвига по фазе между вектором напряжения и вектором тока , поэтому векторы этих величин совпадают по направлению (угол ) рисунок (а)
UR
На индуктивном сопротивлении вектор напряжения и вектор тока сдвинуты на ,причем напряжение опережает ток (рисунок б), а на емкостному – напряжение отстает от тока на такой же угол Минус говорит о противоположном характере сдвига (рисунок в)
| Рис.б) | Рис в) |
С учетом вышесказанного, если расположить вектор тока ( в принятом масштабе отрезок определенной длины) горизонтально, то вектора напряжения на участках согласно схемы будут располагаться так , как на приведенных без масштабных диаграммах
Диаграмма 1.- индуктивное сопротивление больше емкостного сопротивления
U I
Диаграмма 2 — индуктивное сопротивление меньше емкостного сопротивления
Вектор напряжения U на клеммах цепи строится на основе второго закона Кирхгофа как сумма векторов
Величины напряжений на участках. определяются по закону Ома,. А потом с помощью масштаба находятся длины векторов
,
Например U=60В, принимаем масштаб Ми =
10В/см, тогда длина вектора
lu
=60/10=6см
Сделать выводы о проделанной работе.
ЗАДАНИЕ НА РАСЧЕТНО-ГРАФИЧЕСКУЮ РАБОТУ
Неразветвленная цепь переменного тока.
Активное сопротивление R, индуктивность L и емкость C соединены последовательно и подключены к источнику с напряжением U. Исходные данные приведены в таблице 1. Начертить электрическую схему, определить полное сопротивление цепи Z и коэффициент мощности COSj, ток I, напряжение, мощности цепи P, QL,QC, S.
Построить в масштабе векторную диаграмму, треугольники сопротивлений и мощностей.
Расчетные данные для каждого варианта (последняя цифра зачетной книжки) приведены в Таблице 1.
Таблица 1. Исходные данные
| № варианта | R, Ом | XL, Ом | XC, Ом | U, В |
Для пояснения методики расчёта неразветвленной цепи переменного тока приведены методические указания и пример .
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАНИЯ
1.Векторная диаграмма тока и напряжений. Если в неразветвлённой цепи с активным сопротивлением R, индуктивностью L и емкостью C (рисунок 1) протекает синусоидальный ток i=ImSINjt, то мгновенное значение приложенного к цепи напряжения u=ua+uL+uc. Напряжение на активном сопротивлении Ua совпадает по фазе с током в цепи I, напряжение на индуктивности UL опережает ток на 90°, а напряжение на ёмкости UCотстает от тока на 90.
Действующие значения напряжений на участках цепи: Ua=IR; UL=IXL; UC=IXC. Действующее значение напряжения на зажимах цепи получим методом векторного сложения: U=Ua+UL+UC. Построим векторную диаграмму тока и напряжений. Сначала отложим вектор тока I (рисунок 2). Вектор падения напряжения в активном сопротивлении Ua совпадает по фазе с вектором тока I, вектор индуктивного падения UL отложим вверх под углом 90 0 , а вектор емкостного падения напряжения UC— вниз под углом 90 0 к вектору тока I. Сложив векторы напряжений Ua, UL, UC, получим вектор напряжения U, приложенного ко всей цепи. Векторная диаграмма построена для случая, когда XL>XC и цепь имеет активно- индуктивный характер.
При этом условии UL>UC, а напряжение U опережает по фазе ток I на угол j. Если XC>XL, то UC>UL и цепь имеет активно-ёмкостный характер. При этом напряжение U (рис.2) отстаёт по фазе от тока I на уголj. При равенстве реактивных сопротивлений (XL=XC) UL=UC (рисунок32). При этом напряжение U совпадает по фазе с током I (j=0) и цепь носит активный характер.
Этот режим в рассматриваемой цепи называется резонансом напряжений.
2.Треугольники сопротивлений и мощностей. Рассмотрим треугольник напряжений на (рисунок 4а). Один катет этого треугольника выражает активное напряжение Ua, другой – реактивное напряжение цепи UL-UC, а гипотенуза — полное напряжение U. Разделив стороны треугольника напряжений на ток I ,получим треугольник сопротивлений (рисунок 4б), из которого следует, что полное сопротивление цепи равно:
Закон Ома и связь R, I и U
- Главная
- Электротехника и электроника
- Закон Ома
Для начала рассмотрим определения основных электрических величин, далее рассмотрим законы, связывающие эти величины между собой на основе формул и графических зависимостей. Так от простого к сложному и будет развиваться эта статья.
Первым делом следует отметить, что существуют цепи постоянного и переменного тока. Разница между ними в характере протекания электрических величин — в цепях переменного тока ток и напряжение с течением времени изменяются по определенному закону (например, синусоиде). В цепях же тока постоянного с течением времени значение остается константным.
И в первых и во вторых цепях основными величинами будут: ток, напряжение и сопротивление.
Электрический ток
— упорядоченное движение заряженных частиц (электронов) через проводник (проводящую среду) от точки с большим потенциалом, к точке с меньшим потенциалом. Принято говорить, что ток течет от плюса к минусу в цепях постоянного тока. Измеряется в амперах, обозначается “i”.
Электрическое сопротивление
характеризует способность ограничивать значение электрического тока. Измеряется в омах и обозначается r. Величина обратная сопротивлению — проводимость. В зависимости от величины сопротивления материалы классифицируются на: проводники, диэлектрики и изоляторы.
Электрическое напряжение
равняется разности потенциалов между двумя точками. U=f1-f2. Логично, что напряжение может быть и положительной и отрицательной величиной. Единица измерения вольт (В).
Связь между этими величинами описывается законом Ома:
Значение тока в электрической цепи прямо пропорционально величине напряжения и обратно пропорционально сопротивлению. I=U/R — данная формула применима для цепи постоянного тока. Зная две величины, всегда найдем третью.
Для переменного тока формула приобретет вид I=U/Z, где Z — полное сопротивление цепи, которое состоит из активной, емкостной и индуктивной составляющих:
- R
— активное сопротивление (омическое) - XL
— индуктивное сопротивление (присуще катушкам, обмоткам, статору ТГ) — препятствует протеканию тока - XC
— емкостное сопротивление (конденсаторное, встречается у кабеля) — препятствует протеканию напряжения - Z
— реактивное сопротивление (импеданс, полное сопротивление) состоит из двух составляющих: активной (R) и реактивной (X). А реактивное (X) уже состоит из индуктивного (XL) и емкостного (XC)
Графически соотношение между сопротивлениями можно отобразить в форме прямоугольного треугольника (векторное представление).
В цепях переменного тока значения тока и напряжения изменяются с течением времени, согласно определенному закону. Например, по синусоиде:
I=Im*sin(wt+f)
В данной формуле I — это мгновенное значение тока, Im — амплитудное значение.
Амплитудное
— максимальное значение, амплитудное, которое принимает величина за период. В формулах выше это значения с индексом “m” — типа максимальное.
Мгновенное
— значение величины в данный момент времени. Максимальное из мгновенных значений является амплитудным.
Действующее
— такое значение переменного тока, при котором за период в резисторе выделилось бы столько тепла, сколько и в цепи постоянного тока. Именно эти значения показывают наши вольтметры, амперметры. Для синусоиды действующее равно 0,707 от амплитудного. 1/корень(2)=0,707.
Как расчитать шунт для амперметра
Как подключить амперметр?
В зависимости от преобладания определенного характера сопротивления, векторы тока и напряжения будут смещены относительно друг друга:
Чисто активное сопротивление — ток и напряжение совпадают по фазе.
Преобладает индуктивное — значит, как писалось выше, току пройти тяжелее и он отстает от напряжения.
Преобладает емкостная составляющая — ток уходит в отрыв, напряжение тормозится емкостью.
Также цепи переменного тока могут быть однофазными и трехфазными. В трехфазных цепях приняты обозначения фаз: фаза А (желтая, U), фаза B (зеленая, V) и фаза С (красная, W). Как недавно сказали на одном объекте железной дороги: фаза “А” идет на Минск. 
Между собой фазы могут соединяться в различные схемы: звезда, треугольник, зигзаг и прочие более редкие.
Что такое напряжение смещения нейтрали?
Единицы измерения тока, напряжения, сопротивления и прочих электрических величин