Представление синусоидальных токов и напряжений вращающимися векторами на комплексной плоскости и в комплексной форме. Векторные диаграммы токов и напряжений.

Векторные диаграммы и комплексное представление

Векторные диаграммы можно считать вариантом (и иллюстрацией) представления колебаний в виде комплексных чисел. При таком сопоставлении ось Ox соответствует оси действительных чисел, а ось Oy – оси чисто мнимых чисел (положительный единичный вектор вдоль которой есть мнимая единица).

Тогда вектор длиной A

, вращающийся в комплексной плоскости с постоянной угловой скоростью
ω
с начальным углом
φ0
запишется как комплексное число

а его действительная часть

-есть гармоническое колебание с циклической частотой ω

и начальной фазой
φ0
.

Хотя, как видно уже из вышесказанного, векторные диаграммы и комплексное представление колебаний теснейшим образом связаны и по сути представляют собой варианты или разные стороны одного и того же метода, они, тем не менее, обладают своими особенностями и могут применяться и по отдельности.

• Метод векторных диаграмм может излагаться отдельно в курсах электротехники или элементарной физики, если по тем или иным причинам (обычно связанным с умеренным уровнем математической подготовки учащихся и недостатком времени) надо избежать использования комплексных чисел (в явном виде) вообще.

• Метод комплексного представления (который при необходимости или желании может включать и графическое представление, что, правда, совершенно не обязательно и иногда излишне) вообще говоря более мощен, т.к. естественно включает в себя, например, составление и решение систем уравнений любой сложности, в то время как метод векторных диаграмм в чистом виде всё же ограничен задачами, подразумевающим суммирование, которое можно изобразить на одном чертеже.

• Однако метод векторных диаграмм (в чистом виде или в качестве графической составляющей метода комплексного представления) – более нагляден, а значит в некоторых случаях потенциально более надежен (позволяет до некоторой степени избежать грубых случайных ошибок, которые могут встречаться при абстрактных алгебраических вычислениях) и позволяет в некоторых случаях достичь в каком-то смысле более глубокого понимания задачи.

Расчетные формулы для цепи с параллельным соединением ветвей. Метод векторных диаграмм

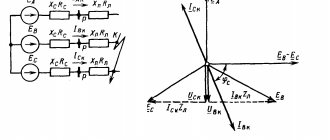
Из векторной диаграммы видно, что все активные составляющие векторов тока направлены одинаково — параллельно вектору напряжения, поэтому векторное сложение их можно заменить арифметическими найти активную составляющую общего тока: Iа = I1a + I2a + I3a.

Реактивные составляющие векторов токов перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, а емкостные — в другую. Поэтому реактивная составляющая общего тока в цепи определяется их алгебраической суммой, в которой индуктивные токи считаются положительными, а емкостные — отрицательными: Ip = — I1p + I2p — I4p + I5p.

Векторы активного, реактивного и полного тока всей цепи образуют прямоугольный треугольник, из которого следует

Подставив величины токов в ветвях, выраженные через напряжение и соответствующие проводимости, получим

где ∑Gn — общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей; ∑Bn — общая реактивная проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (в этой сумме индуктивные проводимости считаются положительными, а емкостные — отрицательными); Y — полная проводимость цепи;

Таким образом получена знакомая уже формула (14.12), связывающая напряжение, ток и проводимость цепи [ср. (14.12) и (14.8)].

Следует обратить внимание на возможные ошибки при определении полной проводимости цепи по известным проводимостям отдельных ветвей: нельзя складывать арифметически проводимости ветвей, если токи в них не совпадают по фазе.

Полную проводимость цепи в общем случае определяют как гипотенузу прямоугольного треугольника, катетами которого являются выраженные в определенном масштабе активная и реактивная проводимости всей цепи:

От треугольника токов можно перейти также к треугольнику мощностей и для определения мощности получить известные уже формулы

Активную мощность цепи можно представить как арифметическую сумму активных мощностей ветвей.

Реактивная мощность цепи равна алгебраической сумме мощностей ветвей. В этом случае индуктивная мощность берется положительной, а емкостная — отрицательной:

Разновидности векторных диаграмм

Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.

С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.

Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.

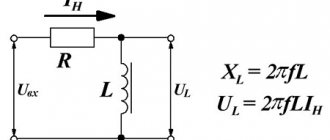
Круговая диаграмма

Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.

Линейная диаграмма

Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.

Механика; гармонический осциллятор

• Гармонический осциллятор в механике и гармонический осциллятор любой природы формально представляют точную аналогию, поэтому рассмотрим их в одном параграфе на примере механического гармонического осциллятора.
• Применение векторных диаграмм в механике сводится в основном к случаю гармонического осциллятора (в том числе имеется в виду и случай осциллятора с линейной по скорости силой трения); впрочем, векторные диаграммы могут быть до некоторой степени полезны и для исследования нескольких осцилляторов в том числе и в пределе бесконечного их количества (для колебаний или волн в распределенных системах).
• С современной точки зрения применение векторных диаграмм к гармоническому осциллятору представляет скорее только исторический и педагогический интерес, однако тем не менее в принципе они здесь вполне применимы.
• В механике применение векторных диаграмм (обычно подразумевается их применение к одномерному осциллятору) имеет ту особенность, что добавляющаяся вторая координата для превращения колебаний во вращение может иметь не только чисто формальный абстрактный смысл, но для одномерной механической системы такого сорта может быть указана механическая же двумерная система, для которой векторная диаграмма первой реализуется как вполне реальное двумерное механическое движение, и все векторы реально двумерны (а после проецирования всех их и движения точки двумерной системы на одну ось, мы получаем мгновенные значения соответствующих величин – в том числе положения – для соответствующей одномерной системы); таким образом, для механической одномерной системы возможна не только формальная математическая, но и реальная механическая
  модель, переводящая колебательное одномерное движение во вращательное движение в двумерном пространстве, реализующая в себе векторную диаграмму для одномерной системы.

Разберем два основных случая простого применения векторных диаграмм в механике (как замечено выше, также применимых к гармоническому осциллятору не только механической, но любой природы): осциллятор без затухания и без внешней силы и осциллятор с (линейным) затуханием (вязкостью), и внешней вынуждающей силой.

Представление синусоидальных функций в виде комплексных чисел

Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.

Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции

i(t) = 10 sin(ωt + 30°).

Данный синусоидальный сигнал можно представить в виде комплексной величины

I = 10∠30°.

Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.

Векторная диаграмма при последовательном соединении элементов

Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.

Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.

Рис. 1. Последовательное соединение элементов цепи

Составим уравнение для данной цепи по второму закону Кирхгофа:

UR + UL + UC = E.

По закону Ома падение напряжений на элементах определяется по следующим выражениям:

UR = I ∙ R,

UL = I ∙ jXL,

UC = −I ∙ jXC.

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.

Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.

При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.

Падение напряжения на резисторе UR совпадает по направлению с током I (т.к. UR = I ∙ R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Падение напряжения на индуктивном сопротивлении опережает вектор тока на 90° (т.к. UL = I ∙ jXL, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Падение напряжения на ёмкостном сопротивлении отстаёт от вектора тока на 90° (т.к. UC = −I ∙ jXC, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелке).

Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи Следует обратить внимание, что на одной векторной диаграмме изображают только векторы тех величин, у которых частота совпадает!

Векторная диаграмма при параллельном соединении элементов

Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.

Рис. 3. Параллельное соединение элементов цепи

Составим уравнение для данной цепи по первому закону Кирхгофа:

I­­ – IR – IL – IC = 0,

откуда

I­­ = IR + IL + IC.

Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:

IR = E / R,

IL = E / (jXL) = −j ∙ E / XL,

IC = E / (−jXC) = j ∙ E / XC,

Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.

При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.

Ток в резисторе IR совпадает по направлению с ЭДС E (т.к. IR = E / R, а R – чисто действительная величина или, простыми словами, нет умножения на мнимую единицу). Ток в индуктивном сопротивлении отстаёт от вектора ЭДС на 90° (т.к. IL = −j ∙ E / XL, а умножение на −j приводит повороту этого вектора на 90° по часовой стрелки). Ток в ёмкостном сопротивлении опережает вектор ЭДС на 90° (т.к. IC = j ∙ E / XC, а умножение на j приводит повороту этого вектора на 90° против часовой стрелки). Результирующий вектор тока определяется после геометрического сложения всех векторов по правилу параллелограмма.

Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи

Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.

Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.

Цепь с резистором и катушкой индуктивности

Цепь переменного тока с этими двумя элементами, включен­ными последовательно, показана на рисунке 4.6, а.

Напряжение, приложенное к катушке, состоит из двух слагаемых: из падения напряжения в активном сопро­тивлении Ua = Ir и индуктивном сопротивлении Ul = I ∙ xL.

Так как вектор падения напряжения Ua совпадает по направлению с вектором тока, а вектор UL опережает его на 90°, то, сложив геометрически оба вектора, по­лучаем вектор напряжения U (рисунок 4.6, б). Таким обра­зом, в цепи с реальной катушкой ток тоже отстает от напряжения, но на угол φ, меньший 90°.

Треугольник АОВ называется треугольником напряже­ний цепи переменного тока, содержащей активное и ин­дуктивное сопротивления.

Из треугольника напряжений вытекают следующие соотношения:

Проекция вектора напряжения на вектор тока называется активной составляющей вектора напряжения и обозначается Ua, а проекция вектора напряжения на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Up. По аналогии вектор тока может быть разложен на активную и реактивную составляющие:

Рисунок 4.7 — Электрическая цепь с резистором, катушкой индуктивности и конденсатором: а) — схема; б) — векторная диаграмма напряжений и тока

Если стороны треугольника напряжений разделить на ток I то получим треугольник сопротивлений (рисунок 4.6, в), катетами которого являются активное r и индуктивное xL сопротивления, а гипотенузой — величина z = , называемая полным сопротивлением цепи.

Ток цепи определяется по закону Ома:

Угол сдвига фаз между током и напряжением опре­деляется из векторных диаграмм (рисунок 4.6, б, в):

или

4.7 Цепь с резистором, катушкой индуктивности и кон­денсатором

На рисунке 4.7 а,представлена электрическая цепь переменного тока, обладающая активным сопротив­лением (резистор), индуктивностью (катушка) и емкостью (конденсатор).

В такой цепи действующее значение приложенного напряжения состоит из трех составляющих: активной Uа, индуктивной UL и емкостной UC: U = Uа + UL + UC (суммирование производится геометрически, рисунок 4.7, б).

Отдельные составляющие действующих значений на­пряжения:

Из векторной диаграммы видно, что активное падение напряжения Uа совпадает с током, индуктивное UL опережает ток на 90°, а емкостное UC отстает от тока на 90°.

Из треугольника напряжений ОАС следует, что напряжение, приложенное к цепи:

Отсюда ток:

Эта формула выражает закон Ома применительно кнеразветвленной цепи переменного тока.

Сдвиг по фазе между напряжением и током определит­ся выражением:

Сопротивление цепи, определяемое формулой:

Называется полным сопротивлением цепи. Сопротивление x = xL — xC называется реактивным.

Возможны следующие случаи соотношений xL и xC:

· xL > xC тогда φ > 0, в цепи преобладает индуктив­ность;

· xL < xC, тогда φ < 0, в цепи преобладает емкость;

· xL = xC, или ω ∙ L = l/ω ∙ C, тогда φ = 0, соs φ = 1.

Сопротивление цепи минимальное, ток достигает при этом наибольшего возможного значения. Напряжения на зажи­мах катушки и конденсатора могут превосходить напря­жение на зажимах цепи в десятки раз. Поэтому резонанс при последовательном соединении элементов называют резонансом напряжений. Резонанс напряжений может воз­никнуть только при небольших активных сопротивлениях цепи. Режим резонанса напряжений в технике сильных токов является аварийным, так как при этом изоляция катушек конденсаторов может быть пробита. В высоко­частотной технике (радиотехнике) резонанс напряжений является нормальным режимом и используется для уси­ления напряжений.

При угловой частоте ш подведенного напряжения ре­зонанс напряжений можно получить путем изменения емкости С или индуктивности цепи L так, чтобы ω ∙ L = 1/ω ∙ С, или при постоянных L и С цепи — путем из­менения частоты подведенного напряжения.

Угловая частота собственных колебаний в контуре ωо = 1/ или частота f = 1/2 ∙ π ∙ , т. е. ωо ∙ L = 1/ ω ∙ С. Следовательно, явление резонанса имеет место при равен­стве частот колебательного контура и источника перемен­ного тока ωо = ω. Угловая частота ωо, при которой на­ступает резонанс, называется резонансной угловой часто той цепи и зависит только от величины индуктивности и емкости цепи.

Рисунок 4.8 — Электрическая цепь с параллельным соединением резистора, катушки индуктивности и конденсатора: а) — схема; б) и в) — векторные диаграммы напряжения и токов; г)ид) — треугольники проводимостей

При резонансе напряжений энергия магнитного поля Wм = L ∙ I2/2 равна энергии электрического поля Wэ = C ∙ U2/2 и передается от катушки к конденсатору и обратно при колебаниях тока и напряжения без потребления энергии от источника. Возникают незатухающие колебания. Обмен энергией между катушкой и конденсатором совершается через источник энергии, который восполняет потери энергии в активных сопротивлениях.

4.8 Параллельное соединение резистора, катушки индук­тивности и конденсатора

В такой цепи (рисунок 4.8, а) дей­ствующее значение тока в неразветвленной части цепи состоит из трех слагаемых: активной Iа, индуктивной IL и емкостной IС:

(суммирование произво­дится геометрически).

Возможны следующие случаи соотношений IC и IL: ток IC > IL тогда φ < 0, ток в неразветвленной части цепи опережает напряжение; вектор Iр (отрезок АС), обозначающий реактивную составляющую тока, направлен вверх от вектора напряжения (рисунок 4.8, б); ток IC < IL, тогда φ > 0, ток в неразветвленной части цепи отстает от напряжения, вектор Iр (отрезок АС) направлен вниз от вектора напряжения (рисунок 4.8, в); ток IC = IL, тогда φ = 0; соs φ = 1, ток в неразветвленной части цепи совпадает по фазе с напряжением и равен активному току, т. е. I = Iа.

Активная составляющая тока Iа имеет один и тот же знак при любых значениях φ. Реактивная составляющая тока меняет знак вместе с изменением знака угла φ. Разделив каждую из сторон треугольника токов на действующее напряжение U, получим треугольник проводимостей (рисунок 4.8, г, д).

Так как соs φ = r/z, a sin φ = x/z, получим выражения для токов и проводимостей при эквивалентном параллельном соединении:

где g = — активная проводимость;

b = bL — bc = xL/z2 — xC/z2 = x/z2 — реактивная проводимость;

y = = — полная проводимость.

Из треугольника проводимостей:

Действующее значение тока в неразветвленной части цепи:

Если разветвленная цепь состоит из соединенных параллельно индуктивности и емкости, то в такой цепи при равенстве ω ∙ L = 1/ω ∙ C возникает явление резонанса токов, при котором токи в ветвях IL и IC (рисунок 4.8, а) равны между собой и могут значительно превышать общий ток I, протекающий в неразветвленной части цепи.

Условия появления резонанса токов аналогичны условиям появления резонанса напряжений.

При резонансе токов вся энергия, подводимая к цепи, расходуется на выделение тепла в активном сопротивлении цепи, а между индуктивностью и емкостью происходит колебательный обмен запасенной энергией.

Режим резонанса токов имеет большое практическое значение. Электрические резонансные контуры используются в радиотехнике, измерительной технике, телеуправлении, различных схемах автоматики. Явления резонанса используются также для изменения параметров линий электропередач. Параллельным подключением емкостей к активно-индуктивной нагрузке повышают коэффициенты мощности нагрузки, разгружая электрические сети от пе­ретоков реактивных мощностей.

Мощность, энергия (работа)

В цепях постоянного тока потребляемая мощность определяется как произведение напряжения на силу тока, энергия (работа) — как произведение мощности на вре­мя. В цепях переменного тока в большинстве случаев такой простой расчет невозможен.

Если цепь переменного тока содержит только актив­ное сопротивление, без индуктивного и емкостного, то активная мощность определяется как произведение дей­ствующих значений напряжения и тока Р = U ∙ I или Р = I2 ∙r. Эта мощность расходуется в активном сопротив­лении и совершает полезную работу.

Обычно в цепи переменного тока наряду с активным сопротивлением есть еще и индуктивное, а часто и емкостное реактивные сопротивления. В таких цепях имеет место сдвиг фаз между током и напряжением, поэтому активная мощность, развиваемая током, меньше произведения U ∙ I, т. е. Р = U ∙ I cos φ.

Единицами активной мощности, как и мощности по­стоянного тока, являются: ватт (Вт), киловатт (кВт), мегаватт (МВт).

Величина cos φ называется коэффициентом мощности цепи переменного тока. Чем больше этот коэффициент, т. е. чем меньше угол сдвига фаз между током и на­пряжением, тем больше активная мощность цепи при тех же значениях тока и напряжения. Поэтому наиболь­шего значения активная мощность достигает в цепях с чисто активным сопротивлением (φ = 0, соsφ = 1), а в цепях с чисто индуктивным сопротивлением активная мощность равна нулю (φ = 90°, cosφ = 0).

Электрическая энергия Wa, расходуемая в цепи пере­менного тока за время t, определяется как произведение активной мощности на время и является активной энер­гией:

.

Рисунок 4.9 — Векторная диаграмма мощностей (треугольник мощностей)

Активная энергия измеряется в киловатт-часах (кВт ∙ ч), и ее расход регистрируется счетчиками активной энергии. Цепь переменного тока характеризуется также реактивной Q и полной S мощностью. Реактивная мощность Q = U ∙ I sin φ. Она является мерой скорости обмена энергией между источником тока и потребителем. Не совершая полезной работы, она служит лишь для создания магнитных полей в индуктивных приемниках (электродвигателях, трансформаторах), циркулируя все время между источником тока и приемниками электрической энергии. Единицей измерения реактивной мощности является вольт-ампер реактивный (вар). Более крупная единица — 1 киловольт-ампер реактивный (квар); 1 квар = 103 вар. Произведение реактивной мощности Q и времени t называется реактивной энергией W ∙ P = Q ∙ t = U ∙ I ∙ t ∙ sin φ.

Реактивная энергия измеряется в киловар-часах (квар ∙ ч). Учет реактивной энергии производится счетчиками реактивной энергии.

Полная мощность S = U ∙ I — это максимально возможная активная мощность при отсутствии сдвига фаз (φ = 0, соs φ = 1). Полная мощность измеряется в вольт-амперах (В ∙ А) или киловольт-амперах (кВ ∙ А). Она является основным параметром, характеризующим генераторы переменного тока и силовые трансформаторы.

Полная, активная и реактивная мощности связаны между собой соотношением:

или

Т.е. таким же соотношением, как и стороны прямоугольного треугольника, катеты которого представляют активную и реактивную мощности, а гипотенуза — полную мощность цепи (рисунок 4.9).

Из треугольника мощностей следует, что:

Активная мощность:

Реактивная мощность:

Алгоритм создания лучевой векторной диаграммы в Excel

Чтобы упростить наш урок, давайте предположим, что мы говорим об отношениях не между четырнадцатью как на графике, а пока только с 4-ма людьми по имени Антон, Алиса, Борис и Белла.

Наша матрица уровня отношений и связей между ними выглядит следующим образом:

• 0 значит отсутствие отношений;
• 1 означает слабые отношения (например: Антон и Алиса просто знают друг друга);
• 2 означает крепкие отношения (например, Борис и Алиса друзья).

Как можно геометрически смоделировать визуализацию этих исходных данных? Если бы мы нарисовали отношения между этими четырьмя людьми (Антон, Алиса, Борис и Белла), это схематически выглядело бы так:

2 критерия, которые нам нужно определить:

1. Расположение точек (где печатаются имена людей).
2. Линии (начальная и конечная точка соединения линий).

Определение и построение точек

Сначала нам нужно построить наши точки таким образом, чтобы промежуток между каждой точкой был одинаковым. Это создаст сбалансированный график.

Какая геометрическая фигура максимально удовлетворяет нашу потребность в таких равных промежутках? Конечно же круг!

Вы можете возразить, что на готовой модели диаграммы нет фигуры круга. Да действительно нет –вот так. Нам не нужно рисовать круг. Нам просто нужно построить точки вокруг него.

Таким образом, у нас есть 4 заинтересованные стороны, нам нужно 4 точки:

1. Если у нас 12 заинтересованных сторон, нам нужно 12 точек.
2. Если у нас есть 20, нам нужно 20 точек.

Предполагая, что источником нашего круга является (x, y), радиус – это r, а тета – 360, деленная на количество нужных нам точек. Первая точка (x1, y1) на окружности будет в этой позиции:

• x1 = x + r * COS (тета);
• y1 = y + r * SIN (тета).

Как только все точки рассчитаны и подключены к XY-диаграмме (точечная диаграмма), давайте двигаться дальше.

Построение линий на лучевой диаграмме

Допустим, у нас в сети есть n человек. Это означает, что каждый человек может иметь максимум n-1 отношений.

Таким образом, общее количество возможных линий на нашем графике равно n * (n-1) / 2.

Нам нужно разделить его на 2, как будто A знает B, тогда B тоже знает A. Но нам нужно нарисовать только 1 линию.

Шаблон лучевой диаграммы для анализа сетевого графика настроен для работы с 20 людьми. Его можно скачать в конце статьи и использовать как готовый аналитический инструмент визуализации данных связей. Это означает, что максимальное количество строк, которое мы можем иметь, будет равно 190.

Каждая строка требует добавления отдельной серии на график. Это означает, что нам нужно добавить 190 серий данных только для 20 человек. И это удовлетворяет только одному типу линии (пунктирная или толстая). Если нам нужны разные линии в зависимости от типа отношений, нам нужно добавить еще 190 серий.

Это больно и смешно одновременно. К счастью, выход есть!

Мы можем использовать гораздо меньшее количество серий и по-прежнему строить один и тот же график.

Допустим, у нас есть 4 человека – A,B,C и D. Ради простоты, давайте предположим, что координаты этих 4-х участников следующие:

• А – (0,0);
• B – (0,1);
• С – (1,1);
• Д – (1,0).

И скажем, A имеет отношения с B, C и D.

Это означает, что нам нужно нарисовать 3 линии, от A до B, от A до C и A до D.

Теперь, вместо того, чтобы поставить 3 серии для диаграммы, что если мы поставим одну длинную серию, которая выглядит следующим образом:

(0,0), (0,1), (0,0), (1,1), (0,0), (1,0)

Это означает, что мы просто рисуем одну длинную линию от A до B, от A до C, от A до D. Договорились, что это не прямая линия, но точечные диаграммы Excel могут нарисовать любую линию, если вы предоставите ей набор координат.

Смотрите эту иллюстрацию, чтобы понять технику:

Таким образом, вместо 190 рядов данных для диаграммы нам просто нужно 20 рядов.

На последнем графике мы имеем 40 + 2 + 1 ряд данных. Это потому что:

• 20 линий для слабых отношений (пунктирные линии);
• 20 линий для прочных отношений (толстые линии);
• 1 строка для выделения синим цветом слабых отношений выделенного участника;
• 1 строка для выделения зеленым цветом сильных отношений выделенного участника;
• 1 комплект без линий, а просто точек для подписей данных на графике.

Как сгенерировать все 20 серий данных:

Это требует следующей логики:

• Предполагая, что нам нужны линии для отношений человека n.
• Точка этого человека будет (Xn, Yn) и уже рассчитана ранее (в точках на графике вокруг круга).
• Нам нужно всего 40 строк данных.
• Каждая нечетная строка будет иметь (Xn, Yn).
• Для каждого четного ряда:
• разделите номер строки на 2, чтобы получить номер человека (скажем, m>);
• (Xn, Yn), если нет отношений между n и m>;
• (Xm, Ym), если есть отношения.

Нам нужны формулы MOD и INDEX для выражения этой логики в Excel.

Как только все координаты линии будут рассчитаны, добавьте их к нашему точечному графику как новые ряды используя инструмент из дополнительного меню: «РАБОТА С ДИАГРАММАМИ»-«КОНСТРУКТОР»-«Выбрать данные» в окне «Выбор источника данных» используйте кнопку «Добавить» для добавления всех 43-х рядов.

Реализовывать создание такой лучевой диаграммы связей будем в 3 этапа:

1. Подготовка исходных данных.
2. Обработка данных.
3. Визуализация.

Подготовка данных для лучевой диаграммы

Как уже упоминалось выше данный шаблон будет обладать возможностью визуального построения связей до 20-ти участников (компаний, филиалов, контрагентов и т.п.). На листе книги шаблона «Данные» предоставленная таблица для заполнения входящих значений. Например, заполним ее для 14-ти участников рынка:

На этом же листе создадим дополнительную таблицу, которая представляет собой матрицу связей всех возможных участников, сгенерированную формулой:

С подготовкой данных мы закончили переходим к обработке.

Как вычислить сумму векторов?

Вектора и матрицы в электронной таблице хранятся в виде массивов.

Известно, что сумма векторов – это вектор, координаты которого равны суммам соответствующих координат исходных векторов:

Для вычисления суммы векторов нужно выполнить следующую последовательность действий:

– В диапазоны ячеек одинаковой размерности ввести значения числовых элементов каждого вектора.

– Выделить диапазон ячеек для вычисляемого результата такой же размерности, что и исходные векторы.

– Ввести в выделенный диапазон формулу перемножения диапазонов

– = Адрес_Вектора_1 + Адрес_Адрес_Вектора_2

– Нажать комбинацию клавиш [Ctrl] + [Shift] +[Enter].

Пример.

Даны два вектора:

Требуется вычислить сумму этих векторов.

Решение:

– В ячейки диапазона А2:A4

введем значения координат вектора a1, а в ячейки диапазона
С2:С4
– координаты вектора a2.

– Выделим ячейки диапазона, в которых будет вычисляться результирующий вектор С (E2:E4

) и введем в выделенный диапазон формулу:

=A2:A4+C2:C4

– Нажмем комбинацию клавиш [Ctrl] + [Shift] +[Enter]. В ячейках диапазона E2:E4

будут вычислены соответствующие координаты результирующего вектора.

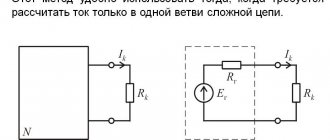
Расчет цепи без определения проводимостей ветвей

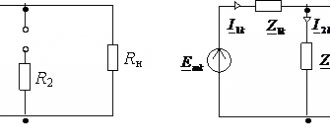
Расчет электрической цепи при параллельном соединении ветвей можно выполнить без предварительного определения активных и реактивных проводимостей, т. е. представляя элементы цепи в схеме замещения их активными и реактивными сопротивлениями (рис. 14.15, а).

Определяют токи в ветвях по формуле (14.4);

где Z1, Z2 и т. д. — полные сопротивления ветвей.

Полное сопротивление ветви, в которую входят несколько элементов, соединенных последовательно, определяют по формуле (14.5).

Для построения векторной диаграммы токов (рис. 14.15, б) можно определить активную и реактивную составляющие тока каждой ветви по формулам

и т. д. для всех ветвей.

В этом случае отпадает необходимость определения углов ф1 ф2 и построения их на чертеже.

Ток в неразветвленной части цепи

Общий ток и мощность цепи определяются далее в том же порядке, какой был показан ранее (см. формулы (14.10), (14.15), (14.16)].