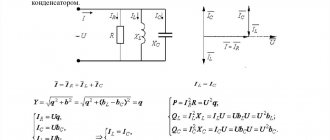
Последовательный резонанс RLC
Рассмотрим схему последовательного резонатора.
RLC цепь
Как уже видно из схемы для описания нам понадобиться записать уравнение входного импеданса.
\Large Z_{in} = R + jwL — j\frac{1}{wC} (1)
Далее, для понимания происходящих процессов, удобно работать с мощностями. Запишем полную мощность в RLC цепи
\Large P = V_{rms} \cdot I_{rms} = \frac{V \cdot I}{ \sqrt{2}\cdot \sqrt{2}} = \frac{V \cdot I}{2} (2)
В уравнение фигурирует корень из двух, поскольку используется действующее значение переменного тока и напряжения.
Теперь запишем мощность в комплексной форме через импеданс из уравнения (1).
\Large P=\frac{I^{2}Z_{in} }{2}= \frac{1}{2} I^{2} \cdot (R + jwL — j\frac{1}{wC})
Раскроем скобки
\Large P=\frac{1}{2} I^{2}R + \frac{1}{2} I^{2}jwL — \frac{1}{2} I^{2}\frac{j}{wC} (3)
На этом моменте остановимся и внимательно посмотрим, что мы получили.
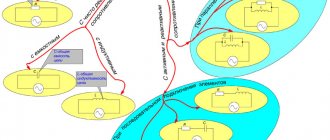
Составляющие уравнения
Для большей очевидности распишем каждую мощность, энергию используя среднеквадратическое (оно же действующие) значение тока или напряжения.
Напомним, что действующее значение для синусоидального сигнала находится как:
\Large V_{rms} = \frac{V_{max}}{\sqrt{2}}
Тогда мощность рассеиваемая на резисторе:
\Large P_{r} = \frac{I^{2}R}{2}
Энергия накапливаемая в индуктивности:
\Large W_{L}= \frac{LI_{rms}^{2}}{4}
Энергия накапливаемая в конденсаторе, но выразив через ток:
\Large W_{C}= \frac{CU_{rms}^{2}}{2} = \frac{I_{rms}^{2}}{4\cdot Cw^{2} }
Вернёмся к выражению (3) и запишем его оперируя мощностями и энергиями из уравнений выше.
\Large P = P_{r} + 2jw(P_{L}-P_{C}) (4)
Отсюда видно, что резонанс возникает когда накапливаемые энергии в конденсаторе и в индуктивности становятся равными. Или, если обратиться к уравнению (1), импеданс индуктивности становится равен импедансу конденсатора. Точка резонанса характерна минимальным входным сопротивлением (Z_in = R).
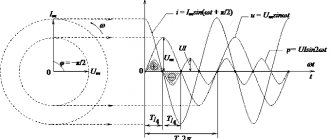
На графике импеданса, последовательный резонанс показан на рисунке ниже.
Импеданс от частоты.
Как уже говорилось, условия для резонанса возникает когда WL=WC. Приравняем две энергии.
\Large \frac{LI_{rms}^{2}}{4} = \frac{I_{rms}^{2}}{4\cdot Cw^{2} }
Отсюда уже легко найти резонансную частоту.
\Large w_{0} = \frac{1}{\sqrt{LC}}
Далее найдём ещё один из важных параметров характеризующий резонансную цепь — это добротность. С помощью добротности часто описывают величину потерь в контуру. Так же с помощью добротности, можно определить насколько RLC цепь в целом подвержена колебаниям.
По сути добротность это — отношение запасаемой (хранящейся) энергии в цикле к энергии потерь. Обозначается как Q.
\Large Q_{0} =w_{0} \frac{W_{stor}}{W_{loss}} = w_{0} \frac{W_{L}+W_{C}}{W_{loss}} (5)
Давайте далее рассмотрим формулу для добротности для резонансной частоты w0. Как уже писалось выше, на частоте резонанса энергия в конденсаторе и в индуктивности равны. Учтём это в формуле (5).
\Large Q_{0} =w_{0} \frac{2W_{L}}{W_{R}} = w_{0} \frac{2\cdot \frac{I^{2}L}{4}}{\frac{I^{2}R}{2}} = w_{0} \frac{L}{R}
То же самое можно расписать через энергию конденсатор.
\Large Q_{0} =\frac{1}{w_{0}RC}
И последнее, что стоит отметить для последовательного резонанса, это полоса пропускания резонанса. Что это такое? На словах это можно описать так: полоса пропускания для резонансной цепи- это область частот, которая лежит внутри границ, где мощность рассеиваемая резистором меньше половины всей мощности системы. Найти ширину полосы можно вот так:
\Large BW = w_{0} \frac{1}{Q_{0}}
Границы полосы можно найти простым способом, например от частоты w0 отступить в каждую сторону по BW/2. Так же это можно сделать через передаточную функцию для RLC цепи по отношению к резистору. Запишем передаточную функцию как отношение Vr/Vin.
\Large \frac{V_{r}}{V_{in}} = \frac{IR}{I(R+jwL+\frac{1}{jwC})} = \frac{R}{R+\frac{(jw)^{2}LC+1}{jwC}}
Далее каждый член уравнения умножаем на jwC/jwC
\Large \frac{V_{r}}{V_{in}} = \frac{jwRC}{jwRC-w^{2}LC+1}
Теперь находим модуль передаточной функции. Напомню, что модуль для комплексных чисел находится как:
\Large \sqrt{(RE)^{2}+(IM)^{2}}
Теперь запишем окончательный вариант модуля передаточной функции.
\Large \left | \frac{V_{r}}{V_{in}} \right | = \frac{wRC}{\sqrt{(wRC)^{2}+(1- w^{2}LC)^{2}}} (6)
После того как мы записали передаточную функцию вернёмся к определению полосы пропускания. Полоса пропускания для резонансной цепи- это область частот, которая лежит внутри границ, где мощность рассеиваемая резистором меньше половины всей мощности системы.
Другими словами, чтобы найти полосу пропускания необходимо задаться условиями, где на резисторе будет рассеиваться половина всей мощности. Для этого амплитуда на резисторе должно быть равна как минимум:
\Large \frac{1}{\sqrt{2}}V_{max}
Зная эти условия, вернёмся к уравнению с учётом вышесказанного (6).
\Large \frac{1}{\sqrt{2}} = \frac{wRC}{\sqrt{(wRC)^{2}+(1- w^{2}LC)^{2}}} (7)
Теперь мы можем решить уравнение (7) относительно w. После решения получаем следующие корни:
\Large w_{1,2} = (\sqrt{1+(\frac{R}{2\sqrt{\frac{L}{C}}})^{2}} \pm \frac{R}{2\sqrt{\frac{L}{C}}})_{w0}
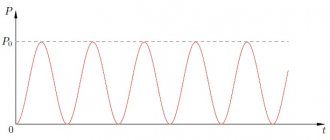
Выделим полученные частоты на графике импеданса, который фигурировал выше.
Полоса пропускания RLC
Параметры для построения.
Листинг mathcad.
Подключение к цепи индуктивной катушки
Резонанс в электрической цепи
Включение в ёмкостную цепь катушки индуктивности сразу превращает её в КК. В зависимости от схемы подключения, различают два вида КК 1 класса: параллельный и последовательный.
Параллельный КК
В данной схеме конденсатор С соединён с катушкой L параллельно. Если заряженный конденсатор присоединить к катушке, то энергия, запасённая в нём, передастся ей. Через индуктивную катушку L потечёт ток, вызывая электродвижущую силу (ЭДС).
ЭДС самоиндукции L будет направлена на снижение тока в параллельной цепи. Ток, созданный этой ЭДС, и ток разряда ёмкости сначала одинаковы, а их суммарное значение равно нулю. Конденсатор передаст свою энергию Ec в катушку и полностью разрядится. Индуктивность, получив максимальную магнитную энергию EL, начнёт заряжать ёмкость напряжением уже другой полярности. Когда вся энергия из индуктивности перейдёт в ёмкость, конденсатор будет полностью заряжен. В цепи появляются колебания, такой контур называется колебательным.
Параллельный КК
К сведению. Если бы в такой цепи отсутствовали потери, то такие колебания никогда не стали затухать. На пpaктике, продолжительность процесса зависит от потери энергии. Чем больше потери, тем меньше длительность колебаний.
Параллельное соединение C и L вызывает резонанс токов. Это значит, что токи, проходящие через C и L, выше по значению, чем ток через сам контур, в конкретное число раз. Это число носит название добротности Q. Оба тока (емкостной и индуктивный) остаются внутри цепи, потому что они находятся в противофазе, и происходит их обоюдная компенсация.
Стоит отметить! На fрез величина R КК устремляется к бесконечности.
Последовательный КК
В этой схеме соединены последовательно друг с другом катушка и конденсатор.
Последовательный КК
В такой схеме происходит resonance напряжений, R контура устремляется к нулю в случае образования резонансной частоты (fрез). Это позволяет использовать подобную систему резонанса в качестве фильтра.
Параллельный резонанс RLC
Опишем всё тоже самое, что выводили для последовательного RLC резонанса, но в более сжатой форме.
Параллельная RLC цепь
Выражение для импеданса Z_in:
\Large Z_{in} = (\frac{1}{R}+\frac{1}{jwL}+jwC)^{-1}
График зависимости импеданса от частоты:
Z_in(w)
Резонансная частота находится так же как и для последовательного резонанса и равна:
\Large w_{0} = \frac{1}{\sqrt{LC}}
Добротность для параллельного резонансного контура:
\Large Q_{0} = \frac{R}{w_{0}L} = w_{0}RC
Ширина полосы пропускания, также как и в последовательном RLC контуре, за исключением, что добротность должна быть для параллельного RLC контура.
\Large BW = w_{0} \frac{1}{Q_{0}}
Определение колебательного контура
Частота вращения: формула
Резонансные явления, отмеченные в электротехнике, ярко выражены в схемах колебательных контуров (КК). Подобные конструкции представляют собой элементарные системы, способные осуществлять свободные колебания электромагнитной природы. Сам КК в цепи состоит из следующих элементов:
- конденсатора;
- катушки индуктивности;
- источника тока.
Внимание! Выводы элементов схемы могут соединяться друг с другом параллельно или последовательно. Все зависит от того, какого результата нужно добиться от резонанса в КК.
Применение колебательных контуров
Подробный расчет колебательного контура позволяет точно подбирать величину необходимых элементов КК. Это позволяет использовать их в схемах электроники в виде:
- частотных фильтров – в радиоприёмниках, генераторах сигналов, преобразователях и выпрямителях;
- колебательных контуров – для выделения и настройки на определённую частоту станции вещания;
- силовых resonance-фильтров – для формирования напряжения синусоидальной формы.
На самолётах гражданской авиации КК применяется в блоках регулировки частоты генераторов.
Польза и вред резонанса
Для того чтобы сделать некий вывод о плюсах и минусах резонанса, необходимо рассмотреть, в каких случаях он может проявляться наиболее активно и заметно для человеческой деятельности.
Положительный эффект
Явление отклика широко используется в науке и технике. Например, работа многих радиотехнических схем и устройств основывается на этом явлении.
- Двухтактный двигатель. Глушитель двухтактного двигателя имеет особую форму, рассчитанную на создание резонансного явления. Оно улучшает работу двигателя засчет снижения потребления и загрязнения. Этот резонанс частично уменьшает несгоревшие газы и увеличивает сжатие в цилиндре.
- Музыкальные инструменты. В случае струнных и духовых инструментов звуковое производство происходит в основном при возбуждении колебательной системы (струны, колонны воздуха) до возникновения явления резонанса.
- Радиоприемники. Каждая радиостанция излучает электромагнитную волну с четко определенной частотой. Для его захвата цепь RLC принудительно подвергается вибрации с помощью антенны, которая захватывает все электромагнитные волны, достигающие ее. Для прослушивания одной станции собственная частота RLC-схемы должна быть настроена на частоту требуемого передатчика, изменяя емкость переменного конденсатора (операция выполняется при нажатии кнопки поиска станции). Все системы радиосвязи, будь то передатчики или приемники, используют резонаторы для «фильтрации» частот сигналов, которые они обрабатывают.
- Магнитно-резонансная томография (МРТ). В 1946 году два американца Феликс Блох и Эдвард Миллс Перселл самостоятельно обнаружили явление ядерного магнитного резонанса, также называемое ЯМР, которое принесло им Нобелевскую премию по физике.
Отрицательное воздействие
Однако не всегда явление полезно. Часто можно встретить ссылки на случаи, когда навесные мосты ломались при прохождении по ним солдат «в ногу». При этом ссылаются на проявление резонансного эффекта воздействия резонанса, и борьба с ним приобретает масштабный характер.
- Автотранспорт. Автомобилисты часто раздражаются шумом, который появляется при определенной скорости движения транспортного средства или в результате работы двигателя. Некоторые слабо закругленные части корпуса вступают в резонанс и излучают звуковые колебания. Сам автомобиль с его системой подвески представляет собой осциллятор, оснащенный эффективными амортизаторами, которые препятствуют возникновению острого резонанса.
- Мосты. Мост может выполнять вертикальные и поперечные колебания. Каждый из этих типов колебаний имеет свой период. Если стропы подвешены, система имеет очень разную резонансную частоту.
- Здания. Высокие здания чувствительны к землетрясениям. Некоторые пассивные устройства позволяют защитить их: они являются осцилляторами, чья собственная частота близка к частоте самого здания. Таким образом, энергия полностью поглощается маятником, препятствующим разрушению здания.
Следующая
РазноеЧто такое активная мощность?