Содержание
- 1 1. Поле внутри проводника
- 2 2. Распределение заряда в проводнике
- 3 3. Поле снаружи проводника вблизи его поверхности
- 4 4. Распределение потенциала в проводнике
- 5 5. Полость внутри проводника
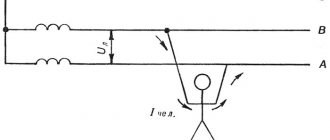
«Хочу сообщить вам новый и страшный опыт, который никак не советую повторять… Вдруг моя правая рука была поражена с такой силой, что все тело содрогнулось, как от удара молнии. …Одним словом, я думал, что пришел конец … Ради французской короны я не согласился бы еще раз подвергнуться столь жуткому сотрясению…» Это слова из воспоминаний лейденского профессора Мушенбрека, приведенные в книге В. Карцева «Приключения великих уравнений». Мушенбрек в 1745 году ставил опыты по электричеству и получил простейший конденсатор, названный впоследствии лейденской банкой. Во время опытов профессор и подвергся «столь жуткому сотрясению» в результате разряда конденсатора через человеческое тело, являющееся, как известно, проводником.
Тот факт, что в природе существуют проводники, обогащает окружающий нас мир разнообразными электрическими явлениями, среди которых есть и далеко небезопасные. Проводники занимают важное место при изучении электромагнетизма.
Рассмотрим подробно случай, когда заряженный неподвижный проводник находится во внешнем электростатическом поле (созданном посторонними неподвижными зарядами). В проводнике рано или поздно все заряды перестанут перемещаться, и наступит равновесие (так как в противном случае мы получили бы вечный двигатель в результате непрерывного выделения тепла при движении зарядов). Для такого заряженного и помещенного во внешнее электростатическое поле проводника будут справедливы утверждения, приведенные ниже.
Распределение заряда в проводнике
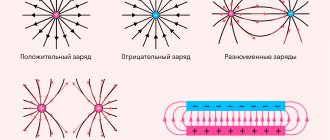
Для того чтобы ответить на вопрос о распределении заряда в проводнике, нам надо уточнить некоторые свойства силовых линий электростатического поля. Напомним, что силовая линия электрического поля (в том числе и электростатического) — это воображаемая линия в пространстве, проведенная так, чтобы касательная к ней в каждой точке совпадала с вектором напряженности электрического поля в этой точке. Опыт изучения электростатических полей дает основание заключить, что силовые линии этих полей непрерывны и не замкнуты, они могут начинаться только на положительных зарядах и оканчиваться только на отрицательных и не могут начинаться (заканчиваться) в точке пространства, где нет зарядов. При графическом изображении поля некоторой системы зарядов число силовых линий, начинающихся или заканчивающихся на каком-либо заряде, пропорционально модулю этого заряда. Отсюда следует, что из любого заряда обязательно выходят (или входят в него) силовые линии.
После сказанного о силовых линиях возвратимся к вопросу о распределении заряда в проводнике. Выделим мысленно произвольный достаточно малый объем ΔV
внутри проводника (рис. 1). Предположим, что этот объем имеет заряд (для определенности, положительный). Тогда из выделенного объема будут выходить силовые линии, т. е. вблизи него будет существовать электрическое поле. Но поля внутри проводника нет. Поэтому выделенный объем должен быть нейтрален. А поскольку этот объем взят нами в произвольном месте внутри проводника, то можно утверждать, что вся «внутренность» проводника нейтральна и, следовательно, весь заряд проводника находится на его поверхности.
Рис. 1
Проводящая сфера.
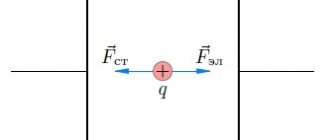
Напряженность поля внутри заряженного проводника равна нулю.В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.
Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.
На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.
Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.
Электрическая емкость шара радиуса R:
Если шар окружен диэлектриком, то:
Поле снаружи проводника вблизи его поверхности
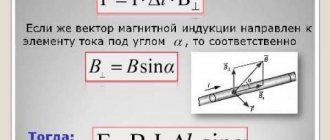
Вектор напряженности электростатического поля в любой точке снаружи проводника вблизи его поверхности направлен перпендикулярно поверхности, что другими словами можно сказать так: силовые линии поля входят в проводник и выходят из него под прямым углом к поверхности проводника. В противном случае существовала бы составляющая вектора напряженности поля вдоль поверхности проводника, на свободные заряды на поверхности проводника действовала бы сила, имеющая составляющую вдоль поверхности. В результате этого по поверхности проводника стали бы двигаться заряды, что нарушило бы равновесие.
Энергия электрического поля
Предположим, что имеется некоторый объем пространства, которое «наполнено» электрическим полем, то есть есть источник поля и благодаря дальнодействию мы говорим, что это пространство наполнено полем. Разумеется, что в виде вещества нет никаких силовых линий поля, это воображаемые в уме представления, но в этой области пространства любой заряд будет реагировать проявлением кулоновской силы. Можно ли как-то характеризовать этот объем пространства энергетически? Так как электрическое поле является потенциальным, то можно говорить о его потенциальной энергии.
Предположим, что вышеозначенный объем пространства — это объем V
внутри плоского конденсатора, а на обкладках конденсатора имеется заряд
Q
. Разность потенциалов между обкладками равна
Δφ
, тогда мы сможем вычислить потенциальную энергию электрического поля по следующей формуле:
Эта формула действительна при условии, что объем является физическим вакуумом, то есть там нет никаких физических частиц. Если же пространство объемом V
будет заполнено веществом, тогда необходимо
ε
(диэлектрическая постоянная) умножить на
ε
— диэлектрическая проницаемость среды (вещества), которым заполнен объем
V
.
Формула тогда имеет вид:
Пример приведен только для энергии поля плоского конденсатора, это всего лишь один случай из многих, но он дает возможность увидеть важные значимые соотношения. Например, из формулы можно узнать, что один литр объема (10-3 м3) при напряжении (разности потенциалов) в 107 Вольт способен запасти лишь незначительное количество энергии, всего лишь 0,44 Джоулей. Это значение для вакуума, но есть такие вещества, которые имеют диэлектрическую проницаемость во много раз больше единицы. Для воды это значение равно 81, а для титаната бария может доходить до 10000. Соответственно во столько же раз увеличивается запасенная энергия.
Дата: 10.05.2015
Распределение потенциала в проводнике
Покажем, что разность потенциалов любых двух точек проводника, включая точки поверхности, равна нулю. Пусть есть произвольные точки М
и
К
внутри проводника. Перенесем мысленно из точки
М
в точку
К
пробный заряд
q
по некоторой траектории
МВК
, лежащей внутри проводника (рис. 2). Силы поля не совершат работы над перемещаемым зарядом
q
, так как поля внутри проводника нет. Поэтому разность потенциалов
φ
M-
φ
K = 0. Если точки
М
и
К
, одна или обе, лежат на поверхности проводника, то доказательство того, что разность потенциалов между ними равна нулю, аналогично.
Рис. 2
Так как разность потенциалов любых двух точек проводника равна нулю, то потенциал всех точек проводника, включая точки поверхности, один и тот же. Поэтому говорят о потенциале проводника, не указывая конкретной его точки. Поскольку все точки поверхности проводника имеют одинаковый потенциал, поверхность проводника будет эквипотенциальной поверхностью.
ИНФОФИЗ
По электрическим свойствам все вещества разделяют на два больших класса — вещества, которые проводят электрический ток (проводники) и вещества, которые не проводят электрический ток (диэлектрики, или изоляторы).
Мы знаем, что все вещества состоят из атомов, которые, в свою очередь, состоят из заряженных частиц. Если внешнее поле вокруг вещества отсутствует, то его частицы распределяются так, что суммарное электрическое поле внутри вещества равно нулю. Если вещество поместить во внешнее электрическое поле, то поле начет действовать на заряженные частицы и они перераспределяться так, что в веществе возникнет собственное электрическое поле. Полное электрическое поле складывается из внешнего поля и внутреннего поля создаваемого заряженными частицами вещества.
Проводник — это тело или материал, в котором электрические заряды начинают перемещаться под действием сколь угодно малой силы. Поэтому эти заряды называют свободными.
В металлах свободными зарядами являются электроны, в растворах и расплавах солей (кислот и щелочей) — ионы.
Диэлектрик — это тело или материал, в котором под действием сколь угодно больших сил заряды смещаются лишь на малое, не превышающее размеров атома расстояние относительно своего положения равновесия. Такие заряды называются связанными.
Рассмотрим подробнее эти классы веществ.
Проводники в электрическом поле.
Проводниками называют вещества, проводящие электрический ток.
Типичными проводниками являются металлы.
Основная особенность
проводников
– наличие
свободныхзарядов
( в металлах это электроны), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.
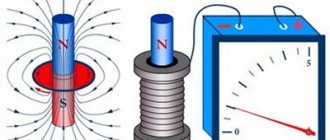
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией
, а появившиеся на поверхности проводника заряды –
индукционными зарядами
.
Явление перераспределения зарядов внутри проводника под действием внешнего электрического поля называется
электростатической индукцией.
Заряды, появляющиеся на поверхности проводника, называются
индукционными зарядами
.
Индукционные заряды создают свое собственное поле , которое компенсирует внешнее поле во всем объеме проводника:
(внутри проводника).
Полное электростатическое поле внутри проводника равно нулю, а потенциалы во всех точках одинаковы и равны потенциалу на поверхности проводника.
Диэлектрики в электрическом поле.
Диэлектриками (изоляторами) называют вещества, не проводящие электрического тока.
В отличие от проводников, в диэлектриках
(изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
При внесении диэлектрика во внешнее электрическое поле в нем возникает некоторое перераспределение зарядов, входящих в состав атомов или молекул. В результате такого перераспределения на поверхности диэлектрического образца появляются избыточные нескомпенсированные связанные
заряды. Все заряженные частицы, образующие макроскопические связанные заряды, по-прежнему входят в состав своих атомов.
Связанные заряды создают электрическое поле , которое внутри диэлектрика направлено противоположно вектору напряженности внешнего поля . Этот процесс называется поляризацией диэлектрика
.
Электрической поляризацией
называют особое состояние вещества, при котором электрический момент некоторого объёма этого вещества не равен нулю.
В результате полное электрическое поле внутри диэлектрика оказывается по модулю меньше внешнего поля .
Физическая величина, равная отношению модуля напряженности внешнего электрического поля в вакууме к модулю напряженности полного поля в однородном диэлектрике , называется
диэлектрической проницаемостью вещества.
Диэлектрическая проницаемость среды показывает, во сколько раз напряженность поля в вакууме больше, чем в диэлектрике.
Это величина безразмерная (нет единиц измерения).
При поляризации неоднородного диэлектрика
связанные заряды могут возникать не только на поверхностях, но и в объеме диэлектрика. В этом случае электрическое поле связанных зарядов и полное поле могут иметь сложную структуру, зависящую от геометрии диэлектрика. Утверждение о том, что электрическое поле в диэлектрике в ε раз меньше по модулю по сравнению с внешним полем строго справедливо только в случае
однородного диэлектрика
, заполняющего все пространство, в котором создано внешнее поле. В частности:
Если в однородном диэлектрике с диэлектрической проницаемостью ε находится точечный заряд q
, то напряженность поля
,создаваемого этим зарядом в некоторой точке, и потенциал φ в ε раз меньше, чем в вакууме:
Существует несколько механизмов поляризации диэлектриков. Основными из них являются ориентационная
,
электронная
и
ионная
поляризации. Ориентационная и электронная механизмы проявляются главным образом при поляризации газообразных и жидких диэлектриков, ионная — при поляризации твердых диэлектриков.
Если двум изолированным друг от друга проводникам сообщить заряды q
1 и
q
2, то между ними возникает некоторая разность потенциалов Δφ, зависящая от величин зарядов и геометрии проводников.
Разность потенциалов Δφ между двумя точками в электрическом поле часто называют напряжением
и обозначают буквой
U
.
Наибольший практический интерес представляет случай, когда заряды проводников одинаковы по модулю и противоположны по знаку: q
1 = –
q
2 =
q
. В этом случае можно ввести понятие
электрической емкости
.
Электроемкостью (электрической емкостью) проводников
называется физическая величина, характеризующая способность проводника или системы проводников накапливать электрический заряд.
Электроемкость находится как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
В системе СИ единица электроемкости называется фарад
[
Ф
]:
Величина электроемкости зависит
от
формы
и
размеров
проводников и от
свойств диэлектрика
, разделяющего проводники.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами
, а проводники, составляющие конденсатор, называются
обкладками
.
Простейший конденсатор – плоский конденсатор
–
система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика
.
Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния
.
В целом ряде задач можно приближенно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.
Электроемкость плоского конденсатора
прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними
.
Если пространство между обкладками заполнено диэлектриком
, электроемкость конденсатора увеличивается в ε раз:
Примерами конденсаторов с другой конфигурацией обкладок могут служить сферический и цилиндрический конденсаторы.
Сферический конденсатор
– это система из двух концентрических проводящих сфер радиусов
R
1 и
R
2.
Цилиндрический конденсатор
– система из двух соосных проводящих цилиндров радиусов
R
1 и
R
2 и длины
L
.
Емкости этих конденсаторов, заполненных диэлектриком с диэлектрической проницаемостью ε, выражаются формулами:
— сферический конденсатор
— цилиндрический конденсатор
Для получения заданного значения емкости конденсаторы соединяются между собой, образуя батареи конденсаторов
.
1) При параллельном соединении
конденсаторовсоединяются их одноименно заряженные обкладки.
Напряжения на конденсаторах одинаковы U
1 =
U
2 =
U,
заряды равны
q
1 = С1
U
и
q
2 = С2
U
.
Такую систему можно рассматривать как единый конденсатор электроемкости C
, заряженный зарядом
q
=
q
1 +
q
2 при напряжении между обкладками равном
U
. Отсюда следует или С = С1 + С2
Таким образом, при параллельном соединении электроемкости складываются.
2) При последовательном соединении конденсаторов
соединяют разноименно заряженные обкладки
Заряды обоих конденсаторов одинаковы q
1 =
q
2 =
q,
напряжения на них равны и
Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q
при напряжении между обкладками
U
=
U
1 +
U
2.
Следовательно, или
При последовательном соединении конденсаторов складываются обратные величины емкостей.
Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.
Т.е. в случае n конденсаторов одинаковой емкости С емкость батареи
при параллельном соединении Собщ = nС
при последовательном соединении Собщ = С/n
Если обкладки заряженного конденсатора замкнуть металлическим проводником, то по цепи пойдет электрический ток, лампочка загорится и будет гореть до тех пор, пока конденсатор не разрядится. Значит, заряженный конденсатор содержит запас энергии.
Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.
Процесс зарядки конденсатора можно представить как последовательный перенос достаточно малых порций заряда Δq
> 0 с одной обкладки на другую.При этом одна обкладка постепенно заряжается положительным зарядом, а другая – отрицательным. Поскольку каждая порция переносится в условиях, когда на обкладках уже имеется некоторый заряд
q
, а между ними существует некоторая разность потенциалов
при переносе каждой порции Δq
внешние силы должны совершить работу
Энергия We
конденсатора емкости
C
, заряженного зарядом
q
, может быть найдена путем интегрирования этого выражения в пределах от 0 до
q
:
Формулу, выражающую энергию заряженного конденсатора, можно переписать в другой эквивалентной форме, если воспользоваться соотношением q
=
CU
.
Электрическую энергию We
следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе.
По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля
.
Полость внутри проводника
Удалим из внутренней области проводника часть вещества. Так как удаляемое вещество нейтрально, то следует ожидать, что электростатическое поле во всех точках вне проводника, внутри проводника и в возникшей полости не изменится. И это будет действительно так, причем на внутренней поверхности проводника (на поверхности полости) зарядов не будет. Весь заряд проводника сосредоточится на внешней поверхности проводника, а наличие полости внутри проводника не скажется на распределении заряда по внешней поверхности. Поле в полости и в проводнике будет отсутствовать. Потенциал всех точек проводника и полости окажется одинаков.
Короче говоря, полый проводник, имеющий заряд и помещенный во внешнее электростатическое поле, ведет себя так же, как и соответствующий сплошной. Доказательство этого утверждения приводить не будем, но заметим, что оно подтверждено многочисленными опытами, проведенными еще Г. Кавендишем (1731-1810) в конце XVIII века и М. Фарадеем (1791-1867) в начале XIX века.