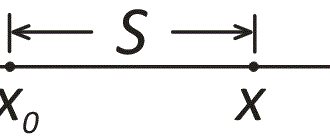Общие сведения
Существует несколько видов взаимодействий. Например, гравитация определяется силой тяжести, а трение и упругость имеют электромагнитную природу. Изучает их электродинамика, одним из разделов которой является электростатика. Суть этой науки заключается в изучении взаимодействия зарядов, находящихся в неподвижном состоянии.
С физической точки зрения, любые тела влияют друг на друга. Между ними всегда действует сила притяжения. Но это явление незаметно из-за слабости существующих сил, связанной с массой тела. В 1600 году физик Уильям Гильберт, проводя эксперименты с янтарём, обнаружил, что если его потереть об шерсть, он начинает притягивать к себе лёгкие предметы. Им было обнаружено, что существует некая субстанция, с помощью которой можно описать новый вид взаимодействия. Получила она название «электростатическое поле».
Этот термин произошёл от слова «электрон», которое с греческого обозначает «янтарь». Было установлено, что в природе существуют силы, вызванные электрическим зарядом. Под ним решили понимать то, присутствие чего на телах вызывает их электростатическое взаимодействие. Сам же этот процесс назвали электризацией. Тела, способные взаимодействовать между собой, стали считать наэлектризованными.
В 1729 году член Парижской Академии наук Шарль Дюфе, изучая силы взаимодействия разных тел, установил, что существует два вида энергии. Один он получал при трении стекла о шёлк (стеклянный), а другой — смолы о шерсть (смоляной). В результате было установлено ключевое отличие возникающих сил от гравитационных. Первые обладали не только притяжением, но и отталкиванием.
Бенджамин Франклин предложил разделять существующие заряды по знаку на положительные и отрицательные. Таким образом, были сформулированы следующие природные свойства:
- каждые тела состоят из элементарных носителей энергии;
- электрический заряд является численной характеристикой;
- частицы с одинаковым знаком отталкиваются друг от друга, а с одноимённым — притягиваются;
- в мире количество положительных зарядов совпадает с числом отрицательных.
То есть при определённом действии, например, трении можно создать условия, при котором в телах произойдёт разделение зарядов, при этом величина их будет одинакова. Этот эффект назвали суперпозицией. Причём между разделёнными частицами возникает электростатическое поле, за энергетическую характеристику которой приняли потенциал.
Для чего нужен потенциометр электрику
Что такое коэффициент мощности
Данный прибор широко применяется в практике для модуляции напряжения. Дело в том, что у многих источников (особенно заточенных под автономное функционирование: аккумуляторные элементы, солнечные батареи и т.д.) константное напряжение, не поддающееся управлению без специальных устройств, что может вызвать проблемы. Чтобы уменьшить исходное напряжение такого элемента, используют устройства-делители, снабженные потенциометрами.
Потенциометр-реостат
Как работает потенциометр? Он представляет собой резистор, имеющий пару выводов и подвижный ползунок с еще одним выводом. Подключаться такое переменное устройство сопротивления может двумя способами:
- По типу реостата, с использованием ползункового вывода и одного из пары других. Сопротивление замеряется движением ползунка по корпусу резистора. Регуляция цепного электротока в таком случае возможна при последовательном подключении такого реостата и источника напряжения.
- Потенциометрическим методом, задействующим каждый вывод из имеющейся у прибора тройки. Два главных вывода включаются параллельно источнику, снятие сниженного напряжения реализуется с ползункового механизма и одного вывода. В этом случае через резисторное устройство течет электроток, создающий спад напряжения между ползунком и боковыми выводами. В такой модели на источник питания ложится большая нагрузка, так как для точности регуляции и отсутствия сбоев необходимо, чтобы резисторное сопротивление в несколько раз уступало нагрузочному.
Потенциометрическое подключение прибора
Таким образом, понятие потенциала используется в разных областях физики: как в механике, так и в изучении электричества. В последнем случае оно выступает в качестве характеристики поля. Непосредственно рассматриваемая величина измерению не поддается, зато можно измерить разность, тогда один заряд берется за точку отсчета.
Работа электростатического поля
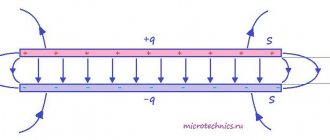
Пусть имеется заряд, находящийся в электрическом поле. На него действует постоянная сила. Если носитель энергии перемещается из одной точки пространства в другую, то говорят о выполнении им работы. В простейшем случае можно рассмотреть однородное поле. В качестве него можно использовать конденсатор. В нём правая пластина пусть будет заряжена положительно, а левая — отрицательно.
Считается, что линии электрического поля будут направлены от плюса к минусу. В некоторой точке этого однородного состояния находится заряд. Для конкретики его можно принять положительным и обозначить буквой A. Под действием сил он перемещается в точку Б. Задача состоит в нахождении работы, совершаемой полем для изменения положения заряженной частицы.
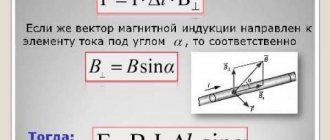
Из механики известно, что такое действие может быть определенно произведением действующей на заряд силы и модуля перемещения, умноженным на косинус угла между ними: A = F * S * cos (a). Так как заряд положительный, то его направление будет совпадать с линиями электрического поля (напряжённостью E). Сила находится по формуле: F = q * E. Тогда, подставляя модуль этого вектора в выражение для работы, можно записать: A = q * E * S * cos (a).
Произведение S * cos (a) представляет собой проекцию отрезка перемещения на направление электрического поля. Изобразить её можно как перпендикуляр, опущенный на E. В результате получится прямоугольный треугольник. Обозначить прилежащий катет (проекцию) можно буквой d. В итоге формула для работы примет вид: A = q * E * d, где:
- q — заряд;
- E — напряжённость;
- d — проекция перемещения.
Пусть заряд перемещается по кривой. Например, проходит путь А-С-В. Значит, будет существовать два вектора S1 и S2. Тогда работа будет определяться как сумма A = Σ ΔAi. То есть если поле однородное (электростатическое), то работа по перемещению заряда не зависит от траектории, а определяется только начальным и конечным положением носителя заряда.
Таким свойством обладают силы тяжести и упругости. Называются они потенциальными. Следовательно, работа по перемещению электричества является такой же. Происходит она за счёт потенциальной энергии заряда, находящего в поле. Поэтому работа равняется уменьшению её значения. Выполненное действие пропорционально заряду, то есть отношению: W / q. Эта величина и получила название «электрический потенциал».
Потенциальная энергия
Вычисляя потенциальную энергию испытательного заряда в этой точке поля, используют свойство, при котором разница потенциальной энергии в двух точках равна работе, выполняемой при перемещении этого значения из одной точки в другую (то же самое делали, включая энергию в гравитационном поле).
Для того чтобы вычислить потенциальную энергию в этой точке, нужно переместить пробный заряд в место, где потенциал равен нулю. Такое место находится в точке, бесконечно отдалённой от источника. Положительный или отрицательный знак потенциала выбирают в зависимости от того, отталкивают груз с источником или притягивают. Если заряд источника является отрицательным, то нахождение электростатического потенциала является таким же. Когда источник является положительным, потенциал — тоже.
Свойства потенциала
Между находящимися частицами в электрическом поле существует напряжение. Оно равно отношению работы к числу заряда. Находят его по формуле: U = A / q. За единицу измерения напряжения принимают вольт. Обозначают его буквой В, характеризуется эта величина отношением джоуль на кулон. Так как разность потенциалов фактически является напряжением, то и измеряют её тоже в этих величинах.
Обозначают электрический потенциал буквой φ (фи). Он позволяет описывать электрическое поле, поэтому его называют энергетической характеристикой. Это скалярная величина. Определяется она как отношение потенциальной энергии заряда к его значению. В то же время напряжённость является силовой характеристикой. Так как эти два явления описывают одно и то же, то между ними существует связь.
Напряжённость позволяет определить силу, действующую на носитель энергии: E = F /q. Если вектор во всех точках пространства имеет одинаковое направление, то поле однородное. В нём на заряд действует сила F, определяемая как произведение заряда на вектор напряжённости. Пусть частица переместилась из А в В. Тогда она пройдёт расстояние d.
Совершённая работа будет определяться как A = q * E * d. Это то же, что A = U * q. Записанные выражения можно приравнять, причём сократить левую и правую часть на q. В результате получится связь между величинами: U = E * d. Так как напряжение — это разность потенциальности начальной и конечной точек, то формулу можно переписать так: φ1 — φ2 = E * d.
Отсюда можно сделать выводы:
- Если в определённой области пространства поля нет (E = 0), значит, φ 1 = φ 2, то есть потенциал равняется константе. Другими словами, φ во всех точках будет одинаковой. Например, во всех точках проводника потенциал будет одним и тем же.
- По сути, потенциальная энергия — это материя, определяющая электрическое взаимодействие тел. Поэтому, чтобы её определить, нужно знать значение φ в начальном положении и после перемещения заряда. Для удобства исходное состояние принимают за ноль. В электротехнике за нулевой уровень потенциал берут величину Земного шара. В теоретической же физике считается, что φ = 0 в бесконечности. Там, где нет электрического поля.
- Эквипотенциальные поверхности и силовые линии взаимно перпендикулярны.
Для понимания следует дать определение эквипотенциальной поверхности. За неё принимают пространство, во всех точках которого потенциал одинаков.
Решение задач
Для успешного решения заданий, связанных с электрическим потенциалом, нужно не только знать несколько формул, но и понимать суть явления. Кроме этого, часто приходится пользоваться справочником по электрофизике. Например, для выяснения массы зарядов.
Вот несколько типовых задач, рассчитанных на самостоятельную проработку учащимися в рамках школьной программы:
- В проводнике на удалении друг от друга находятся два точечных заряда q1 = 100 нКл и q2 = 10 нКл. Расстояние между ними равно 10 сантиметров. Найти их потенциальную энергию. Для решения задачи нужно использовать то, что сила взаимодействия зарядов определяется законом Кулона: F = k * q / r, где k — справочная величина (электрическая постоянная). Учитывая, что φ = q / (4 * p * E0 * r), для рассматриваемого случая можно записать: E = (q1 * q2) / (4 * p * E0 * r) = (10-7 * 10-8) / (4 * 3,14 * 8,85 * 10-12 * 0,1) = 9 * 10-5 Дж.
- Электрический заряд из точки А переместился в В. При этом появилось напряжение, равное 1 кВ. Работа, затраченная на перемещение, составила 40 мкДж. Определить значение заряда. Используя то, что напряжение — это разность потенциалов, находимая как отношение работы к величине энергии: Δ φ = A / q, решить пример можно в одно действие: q = A / U = 400 * 10-6 Дж / 1 * 103 В = 40 * 10-9 Кл.
- Сферу из металла радиусом в один метр положили на пол. Её заряд составляет 10-6 Кл. Определить, во сколько раз снизится потенциал поля сферы на расстоянии 60 см от центра шара, если его радиус увеличится в 3 раза. Исследуемая точка находится внутри тела. Так как в этом случае потенциал точки в середине и на поверхности одинаков, то он зависит от радиуса сферы: φ1 = K * q / r. В итоге он станет втрое меньше, чем вначале: φ2 = K * q / 3r.
- При перемещении точечного заряда q =10 нКл из бесконечности в точку, находящуюся на расстоянии r = 10 см от поверхности заряженной сферы, была выполнена работа А = 0,5 мкДж. Радиус шара составляет 4 см. Вычислить поверхностный потенциал. Решение примера будет выглядеть так: φ = A * (R + r) / q0 * R = 0,5 *10-6 Дж * (0,2 м + 0,0 4 м) / 10 * 10-9 Кл * 0, 2 м = 3 *102 В = 0,3 кВ.
Таким образом, решать задачи, связанные с потенциалом, просто. Но при этом важно следить, в чём должны измеряться подставляемые величины. Все вычисления выполняют в Международной системе единиц (СИ).
Эквипотенциальные поверхности
Если предположить, что источником электрополя является точечно заряженная частица (т. е. поле центральное), из этого следует, что все точки пространства, которые находятся от него одинаково далеко, имеют равный потенциал. В пространстве совокупность таких точек образует поверхность шара, а заряд-источник находится в центре сферы.
Однако, если электрополе не имеет централизованного характера, всё равно можно назначить такие поверхности, что пробный заряд, размещённый в любой точке этой поверхности, будет иметь тот же потенциал. Например, в случае однородного поля такой поверхностью является любая плоскость, перпендикулярная линии поля.