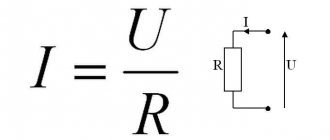При электризации выполняется закон сохранения заряда. Его в 1843 году сформулировал и подтвердил с помощью эксперимента Майкл Фарадей, английский химик и физик – экспериментатор. Этот закон выполняется для любой замкнутой системы.
Примечание: Чтобы система зарядов была замкнутой, в нее не должны проникать дополнительные заряды снаружи, а принадлежащие этой системе заряды не должны ее покидать.
Формулировка и суть закона
Алгебраическая сумма зарядов, находящихся в электрически замкнутой системе, постоянна и всегда сохранятся (не изменяется) – так формулируется закон сохранения заряда. Стоит упомянуть и об определении самой электрически замкнутой системы – ею считается та, через которую не могут проникать заряды. В этой же системе не может возникнуть заряд лишь одного знака, то есть абсолютно всегда при появлении положительного заряда q + q_+ q+ появляется и отрицательный заряд q − q_- q−.
Математический вид закона сохранения заряда
q 1 + q 2 + q 3 + . . . + q n = c o n s t q_1 + q_2 + q_3 +…+q_n=const q1+q2+q3+…+qn=const
Сумма всех зарядов сохраняется. При суммировании зарядов нужно учитывать их знак. К тому же все заряды никак не зависят от скорости, следовательно, они релятивистски инвариантны. Существуют достаточно простые эксперименты, а также задачи, способные это подтвердить.
Рассмотреть данный закон в действии можно в процессе решения следующих задач.
Электризация тел
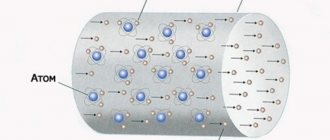
Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.
Способы электризации:
- трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
- через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
- при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
- при ударе;
- под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.
Задача 1
Есть два абсолютно одинаковых металлических шарика, заряды которых равны соответственно 3 q 3q 3q и − 5 q -5q −5q. Какими станут их заряды после соприкосновения?
Решение
В этом конкретном примере можно использовать основную формулу сохранения заряда. Применив ее, получим следующее:
q 1 + q 2 = q 1 ′ + q 2 ′ q_1+q_2=q_{1′}+q_{2′} q1+q2=q1′+q2′
q 1 + q 2 q_1+q_2 q1+q2 — сумма зарядов до соприкосновения; q 1 ′ + q 2 ′ q_{1′}+q_{2′} q1′+q2′ — сумма зарядов после соприкосновения. Согласно закону сохранения электрического заряда эти обе суммы должны быть равны друг другу.
Исходя из того, что шарики одинаковые, можно сказать, что после соприкосновения они обменяются зарядами так, что:
q 1 ′ = q 2 ′ = q ′ q_{1′}=q_{2′}=q’ q1′=q2′=q′
Далее:
q 1 ′ + q 2 ′ = q ′ + q ′ = 2 q ′ ⇒ q ′ = ( q 1 ′ + q 2 ′ ) / 2 = ( q 1 + q 2 ) / 2 q_{1′}+q_{2′}=q’+q’=2q’ ⇒ q’= (q_{1′}+q_{2′})/2=(q_1+q_2)/2 q1′+q2′=q′+q′=2q′⇒q′=(q1′+q2′)/2=(q1+q2)/2
Берем в расчет и то, что один шарик заряжен положительно, а другой – отрицательно. Получаем:
q ′ = ( 3 q − 5 q ) / 2 q’=(3q-5q)/2 q′=(3q−5q)/2
q ′ = − q q’= -q q′=−q
Ответ: − q . -q. −q.
Итак, после соприкосновения шаров их заряды станут − q -q −q.
Теперь разберем более сложный пример с шариками, висящими на нитях.
Сохранение энергии в электрических цепях
Неподвижные электрозаряды обладают потенциальной электростатической энергией.
Энергия электрической цепи — это сумма энергии, которую имеют конденсаторы, катушки индуктивности и прочие элементы.
Закон сохранения энергии для любой электроцепи можно записать в таком виде:
В зависимости от характера движения электрона или протона, а также от природы сил, возникающих между данными частицами, изменение энергии может проявляться как протекание электротока, механическая работа, передача теплоты, изменение внутреннего состояния тел, распространение электромагнитных колебаний и тому подобное.
Применение закона сохранения энергии и электрического заряда позволяет рассчитать механические силы, действующие в электрополе, намного проще по сравнению с тем методом, при котором рассматривается непосредственное действие поля на отдельные элементы системы.
Немного истории
В XVIII веке было установлено, что существует два рода зарядов, которым даны определения «положительный» и «отрицательный» соответственно. Закон сохранения заряда был сформулирован Франклиным, но только 100 лет спустя Майкл Фарадей смог подтвердить и экспериментально установить, что он действителен.
Еще спустя столетие Роберт Милликен и Харви Флетчер провели эксперимент, целью которого являлось установление значения элементарного электрического заряда (заряда электрона). Опыт проводился при помощи двух металлических пластин и наэлектризованной капельки масла. Суть заключалась в том, что если между этими пластинами создать электрическое поле, то капелька прекратит свое падение и будет «парить» в воздухе. Через два года усердной работы Миллер и Флетчер доказали, что электрический заряд – дискретная величина. Подобное утверждение было сделано на основе того, что все результаты, получившиеся в ходе эксперимента, оказались кратными некоторой величине, приблизительно равной e = 1 , 6 ⋅ 1 0 − 19 e=1,6 \cdot 10^{-19} e=1,6⋅10−19 Кл. Это и есть заряд электрона.
Формула нахождения заряда
Определить искомую величину можно из физико-математической формулы силы тока. В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон.
Обратите внимание! Формула заряда является следствием прямой зависимости напряженности электромагнитного поля от потенциала его частицы, что является основным правилом нахождения емкости заряженного конденсатора и величины энергии, накопленной в нём. Кроме того, вычислить количество заряда можно через силу Лоренца.
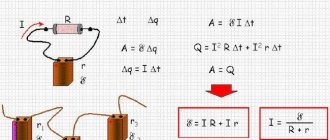
Основные формулы
Способы измерения
Самый простой прибор для измерения – электроскоп. Он состоит из двух лепестков из фольги, расположенных на металлическом стержне. Конструкция накрыта стеклянным колпаком.
Если наэлектризованным телом прикоснуться к стержню, то лепестки наэлектризуются. Поскольку знаки на них одинаковые, то кулонова сила оттолкнёт их в разные стороны. По величине угла отклонения можно оценить величину статического электричества поступившего на лепестки.
Более сложный прибор – электрометр (схематическое изображение на рис. 8). Прибор состоит из стержня электрометра, стрелки и шкалы. Принцип действия аналогичен электроскопу (стрелка отталкивается от стержня). Благодаря наличию шкалы отклонение стрелки электрометра показывает количественную величину переданного электричества.
Рис. 8. Схематическое изображение электрометра
Мы уже упоминали, что Кулон в своих опытах пользовался крутильными весами. Этот измерительный прибор позволил учёному открыть знаменитый закон, названный в честь его имени.
Опыт Милликена
Пусть и не с беспрецедентной точностью, но ему одним из первых удалось выразить заряд цифрой. Это Роберт Милликен — американский физик-экспериментатор.
Раз в составе атома есть мобильные частицы, способные взаимодействовать с себе подобными частицами внутри прочих атомов, они, вероятнее всего, являются базисом электрических процессов, если последние рассматривать на атомном уровне. Следовательно, частицы эти обладают неким свойством, что позволяют им при взаимодействии и перераспределении «переносить» вместе с собой электричество — можно грубо сказать, что электричество как бы в них «вшито».
⚡ Второе предположение представим в виде цепочки размышлений:
- электричество — нечто вроде свойства субатомных частиц;
- внутри атома находятся два разных вида чем-то похожих друг на друга по «электрическим свойствам» частиц — протоны и электроны;
- частицы эти по свойствам взаимно исключаются, так как обычно атом находится в состоянии покоя;
- электроны мобильнее протонов, ведь протоны сконцентрированы в ядре;
- тогда если измерить количество «электрического свойства» для индивидуального электрона, аналогичное будет работать и для протона.
Попробуем же посчитать это количество. Пусть снизу у нас имеется тело с переизбытком электронов, а сверху тело с недостатком электронов. Если тела объединить в единую систему, они создадут зону взаимного притяжения — атомы с переизбытком электронов будут стремиться «скинуть» лишнее в сторону, где преобладает недостаток.
Это создает своего рода кинетический поток, поэтому помещенное между данными телами иное тело также начнет двигаться, от переизбытка к недостатку. Тело, правда, нужно маленькое, чтобы оно, во-первых, двигалось, а, во-вторых, плотное, дабы не создавало лишних проблем с подсчетом массы.
Капельки масла — что может быть лучше. На капельку, падающую в обычных условиях, действует две силы — сила гравитации $m\vec{g}$ и сила сопротивления среды $F_{С}$. Движение при этом под действием силы гравитации происходит вниз. С помощью специального устройства можно зафиксировать предельную скорость падения, когда сила сопротивления сравнивается с гравитационной.
Равнодействующая сил в таком случае равна нулю, и тело, как следствие, падает равномерно, не в ускоренном состоянии. Это позволит рассчитать вес и массу.
Когда капелька начинает движение под действием электрической силы, интересно, что направление движения меняется: электрическая сила в нашем эксперименте превосходит гравитационную и аэродинамическую. Можно также дождаться нуля равнодействующей, за счет этого определить предельную скорость подъема, что позволит нам в свою очередь вычислить, сколько электрической силы действует на капельку.
Электрическая сила отличается по своему «нутру» от механических сил: к примеру, и гравитационная сила, и электрическая обе действуют на объект без прямого контакта, условно на расстоянии, однако при этом электрическая сила явно действует не на массу, а как раз обуславливается количеством в теле «электрического свойства». Чем больше количество «электрического свойства», тем больше электрическая сила, — по аналогии, чем больше масса, тем быстрее тело притягивается к Земле.
В общей сложности, «электрическое свойство» — такая же фундаментальная единица, как и масса. Простой итог: «электрическое свойство» субатомных частиц было принято наречь электрическом зарядом.
Милликен, измеряя показатели электрической силы для множества масляных капель в описанном нами выше эксперименте, увидел потрясающую закономерность. Численное значение заряда капелек все время выходило кратным одному и тому же числу. Это полностью вписывалось в понимание на тот момент атомного строения вещества: в капельке ну никак не может быть $4.54$ электрона — их либо $4$, либо $5$.
Примерно число по расчетам было следующее:
$$1.6\cdot10^{-19}$$