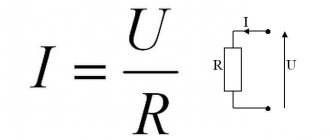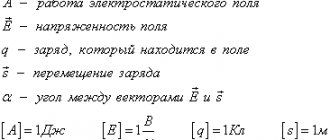During electrification, the law of conservation of charge is satisfied. It was formulated and confirmed experimentally in 1843 by Michael Faraday, an English chemist and experimental physicist. This law holds true for any closed system.
Note: For a system of charges to be closed, additional charges from the outside must not penetrate into it, and charges belonging to this system must not leave it.
Formulation and essence of the law
The algebraic sum of charges located in an electrically closed system is constant and will always be conserved (does not change) - this is how the law of conservation of charge is formulated.
It is worth mentioning the definition of the electrically closed system itself - it is considered to be one through which charges cannot penetrate. In the same system, a charge of only one sign cannot arise, that is, absolutely always when a positive charge q + q_+ q+ appears, a negative charge q − q_- q− also appears. Mathematical form of the law of conservation of charge
q 1 + q 2 + q 3 + . . . + qn = const q_1 + q_2 + q_3 +…+q_n=const q1+q2+q3+…+qn=const
The sum of all charges is maintained. When summing charges, their sign must be taken into account. In addition, all charges do not depend on speed in any way, therefore, they are relativistically invariant. There are quite simple experiments, as well as tasks that can confirm this.
You can consider this law in action in the process of solving the following problems.
Electrification of bodies
Electrification is the process of imparting an electric charge to the body, i.e., violating its electrical neutrality. The process of electrification is the transfer of electrons or ions from one body to another. As a result of electrification, the body gains the opportunity to participate in electromagnetic interaction.
Methods of electrification:
- friction, for example, electrification of an ebonite stick when rubbing against fur. When two bodies come into close contact, some electrons transfer from one body to another; As a result, a deficiency of electrons is created on the surface of one of the bodies and the body receives a positive charge, while the other has an excess, and the body becomes negatively charged. The charges of the bodies are the same;
- through influence (electrostatic induction) - the body remains electrically neutral, the electric charges inside it are redistributed so that different parts of the body acquire charges of different signs;
- When a charged and uncharged body comes into contact, the charge is distributed between these bodies in proportion to their sizes. If the sizes of the bodies are the same, then the charge is distributed equally between them;
- upon impact;
- under the influence of radiation - under the influence of light, electrons can escape from the surface of the conductor, and the conductor acquires a positive charge.
Problem 1
There are two absolutely identical metal balls, the charges of which are equal to 3 q 3q 3q and − 5 q -5q −5q, respectively. What will their charges be after contact?
Solution
For this particular example, the basic formula for conservation of charge can be used. Applying it, we get the following:
q 1 + q 2 = q 1 ′ + q 2 ′ q_1+q_2=q_{1′}+q_{2′} q1+q2=q1′+q2′
q 1 + q 2 q_1+q_2 q1+q2 - sum of charges before contact; q 1 ′ + q 2 ′ q_{1′}+q_{2′} q1′+q2′—sum of charges after contact. According to the law of conservation of electric charge, these two sums must be equal to each other.
Based on the fact that the balls are identical, we can say that after contact they will exchange charges so that:
q 1 ′ = q 2 ′ = q ′ q_{1′}=q_{2′}=q' q1′=q2′=q′
Further:
q 1 ′ + q 2 ′ = q ′ + q ′ = 2 q ′ ⇒ q ′ = ( q 1 ′ + q 2 ′ ) / 2 = ( q 1 + q 2 ) / 2 q_{1′}+q_{ 2′}=q'+q'=2q' ⇒ q'= (q_{1′}+q_{2′})/2=(q_1+q_2)/2 q1′+q2′=q′+ q′=2q′⇒q′=(q1′+q2′)/2=(q1+q2)/2
We also take into account that one ball is charged positively and the other negatively. We get:
q ′ = ( 3 q − 5 q ) / 2 q'=(3q-5q)/2 q′=(3q−5q)/2
q ′ = − q q'= -qq′=−q
Answer: − q. -q. −q.
So, after the balls touch, their charges will become − q -q −q.
Now let's look at a more complex example with balls hanging on threads.
Energy conservation in electrical circuits
Stationary electric charges have potential electrostatic energy.
The energy of an electrical circuit is the sum of the energy that capacitors, inductors and other elements have.
The law of conservation of energy for any electrical circuit can be written as follows:
Depending on the nature of the movement of an electron or proton, as well as on the nature of the forces arising between these particles, a change in energy can manifest itself as the flow of electric current, mechanical work, heat transfer, a change in the internal state of bodies, the propagation of electromagnetic oscillations, and the like.
The application of the law of conservation of energy and electric charge makes it possible to calculate the mechanical forces acting in an electric field much easier compared to the method that considers the direct action of the field on individual elements of the system.
A little history
In the 18th century, it was established that there are two types of charges, which are defined as “positive” and “negative”, respectively. The law of conservation of charge was formulated by Franklin, but it was not until 100 years later that Michael Faraday was able to confirm and experimentally establish that it was valid.
A century later, Robert Millikan and Harvey Fletcher conducted an experiment whose purpose was to establish the value of the elementary electric charge (electron charge). The experiment was carried out using two metal plates and an electrified drop of oil. The idea was that if an electric field is created between these plates, the droplet will stop falling and will “float” in the air. After two years of hard work, Miller and Fletcher proved that electric charge is a discrete quantity. A similar statement was made on the basis that all the results obtained during the experiment turned out to be multiples of a certain value approximately equal to e = 1.6 ⋅ 1 0 − 19 e=1.6 \cdot 10^{-19} e=1 .6⋅10−19 Cl. This is the charge of the electron.
Formula for finding charge
The required value can be determined from the physical and mathematical formula for current strength. In accordance with it, you need to multiply the current strength by the time it passes through the conductor. The amount of charge can be found through the formula +-ne, where n is an integer and e is equal to the value = -1.6*10^-19 Coulomb.
Note ! The charge formula is a consequence of the direct dependence of the electromagnetic field strength on the potential of its particle, which is the basic rule for finding the capacity of a charged capacitor and the amount of energy accumulated in it. In addition, the amount of charge can be calculated using the Lorentz force.
Basic formulas
Measurement methods
The simplest measuring device is an electroscope. It consists of two foil petals located on a metal rod. The structure is covered with a glass cover.
If you touch the rod with an electrified body, the petals become electrified. Since the signs on them are the same, the Coulomb force will push them in different directions. By the magnitude of the deflection angle, you can estimate the amount of static electricity received by the petals.
A more complex device is an electrometer (schematic representation in Fig. 8). The device consists of an electrometer rod, a pointer and a scale. The principle of operation is similar to an electroscope (the arrow is repelled from the rod). Thanks to the presence of a scale, the deflection of the electrometer needle shows the quantitative value of the transferred electricity.
Rice. 8. Schematic representation of an electrometer
We have already mentioned that Coulomb used torsion balances in his experiments. This measuring device allowed the scientist to discover the famous law named after him.
Millikan experience
Although not with unprecedented accuracy, he was one of the first to express charge in numbers.
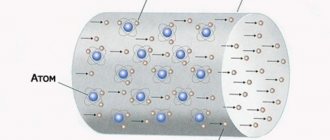
This is Robert Millikan, an American experimental physicist. Since the atom contains mobile particles that are capable of interacting with similar particles inside other atoms, they are most likely the basis of electrical processes, if the latter are considered at the atomic level. Consequently, these particles have a certain property that allows them, during interaction and redistribution, to “carry” electricity with them - we can roughly say that electricity is, as it were, “sewn into them.”
⚡ Let's present the second assumption in the form of a chain of thoughts :
- electricity is something like a property of subatomic particles;
- inside an atom there are two different types of particles somewhat similar to each other in terms of their “electrical properties” - protons and electrons;
- These particles are mutually exclusive in their properties, since usually the atom is at rest;
- electrons are more mobile than protons, because protons are concentrated in the nucleus;
- then if you measure the amount of “electrical property” for an individual electron, the same will work for a proton.
Let's try to calculate this amount. Let us have a body below with an excess of electrons, and above a body with a lack of electrons. If bodies are combined into a single system, they will create a zone of mutual attraction - atoms with an excess of electrons will tend to “throw off” the excess in the direction where the deficiency predominates.
This creates a kind of kinetic flow , so another body placed between these bodies will also begin to move, from excess to deficiency. The body, however, needs to be small so that, firstly, it moves, and, secondly, it needs to be dense so that it does not create unnecessary problems with calculating the mass.
Drops of oil - what could be better? A droplet falling under normal conditions is subject to two forces: the gravitational force $m\vec{g}$ and the drag force of the medium $F_{C}$. In this case, the movement occurs downward under the influence of gravity. Using a special device, you can record the maximum speed of fall when the resistance force is compared with gravitational force.
The resultant force in this case is zero, and the body, as a result, falls uniformly, not in an accelerated state. This will allow you to calculate the weight and mass.
When a droplet begins to move under the influence of an electric force, it is interesting that the direction of movement changes: the electric force in our experiment exceeds the gravitational and aerodynamic ones. We can also wait until the resultant is zero, thereby determining the maximum rate of rise , which will allow us, in turn, to calculate how much electrical force acts on the droplet.
Electrical force differs in its “guts” from mechanical forces: for example, both gravitational force and electric force both act on an object without direct contact, conditionally at a distance, however, the electric force clearly does not act on mass, but is precisely determined by the amount body of "electrical properties". The greater the amount of "electrical property", the greater the electrical force - by analogy, the greater the mass, the faster the body is attracted to the Earth.
In general, the “electrical property” is as fundamental a unit as mass. A simple result: the “electrical property” of subatomic particles was called electric charge .
Millikan, measuring the electrical force for many oil drops in the experiment we described above, saw a stunning pattern. The numerical value charge always turned out to be a multiple of the same number. This fully fit into the understanding of the atomic structure of matter at that time: there could be no way that there could be $4.54$ electrons in a droplet—there were either $4$ or $5$.
The estimated number was as follows:
$$1.6\cdot10^{-19}$$