- Как определяют разность потенциалов Как связаны напряженность однородного электростатического поля и разность потенциалов
Работа по перемещению заряда в электростатическом поле:
В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными
, а само поле называется
потенциальным
.
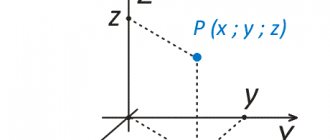
Пусть точечный заряд `q` находится в однородном электрическом поле с напряжённостью `vecE`. (Обобщение на случай неоднородного поля см. ниже.) Тогда со стороны поля на него действует сила `vecF=qvecE`. Рассмотрим перемещение этого заряда из точки `1`, характеризуемой радиус — вектором `vecr_1`, в точку `2` — с радиус — вектором `vecr_2` по, вообще говоря, криволинейной траектории (рис. 11). Мысленно разобьём всю траекторию на большое число малых перемещений `Deltavecr_i`, так что `Deltavecr=vecr_2-vecr_1=sum_i Deltavecr_i`, где все векторы `Deltavecr_i` считаем сложенными по правилу многоугольника.
Работой силы со стороны электрического поля при перемещении заряда `q` из точки `1` в точку `2` называют величину (сумму работ на отдельных участках)
`A_(12)=sum_i vecF_i Deltavecr_i`, (1.4.1.)
где `vecF_i` — сила, действующая на заряд на малом участке `Deltavecr_i`, `vecF_iDeltavecr_i` — скалярное произведение векторов. В нашем случае (однородного электрического поля) сила на всех участках одна и та же, `vecF=qvecE`, поэтому получаем
`A_(12)=sum_i vecF_i Deltavecr_i= qvecE sum_i Deltavecr_i=qvecE(vecr_2-vecr_1)`. (1.4.2)
Заметим, что работа силы электростатического поля (1.4.2) определяется лишь начальной и конечной точками (двумя радиус-векторами `vecr_1` и `vecr_2`) и не зависит от конкретной траектории, по которой двигался заряд (в ответ вошла лишь разность этих векторов). Силы, обладающие тем свойством, что работа этих сил не зависит от траектории, называют консервативными силами, а соответствующие поля — потенциальными полями. Не все силы обладают этим свойством; пример неконсервативной силы — сила трения. Другой важный пример не потенциального поля (и неконсервативной силы) — изменяющееся со временем электрическое поле.
По общей теореме механики изменение кинетической энергии заряда равно сумме работ всех сил:
`(mv_2^2)/2 — (mv_1^2)/2 =A_(12)^(«всех сил»)`. (1.4.3)
Если заряд двигался только под действием сил электрического поля (не было никаких ниточек, за которые бы мы тянули заряд, не было силы трения и др.), то вместо (1.4.3) (и согласно (1.4.2)) имеем:
`(mv_2^2)/2 — (mv_1^2)/2 =qvecE(vecr_2-vecr_1)`. (1.4.4)
Последнее равенство перепишем ещё в форме
`(mv_2^2)/2 -qvecEvecr_2= (mv_1^2)/2-qvecEvecr_1`, (1.4.4′)
которая допускает следующую важную трактовку. Скажем, что заряд `q` в однородном электростатическом поле обладает потенциальной энергией
`Pi(vecr)=-qvecEvecr+Pi_0`, (1.4.5)
где `Pi_0` — произвольная константа. Тогда с учётом того, что `K=(mv^2)/2` — кинетическая энергия заряда, равенство (1.4.4’) – это просто закон сохранения энергии:
`K_2+Pi_2=K_1+Pi_1`, (1.4.6)
т. е. в процессе движения сумма кинетической и потенциальной энергий не изменяется (сохраняет своё значение).
Если приписать точке `A` с радиус-вектором `vecr_0` потенциальную энергию, равную нулю, то это эквивалентно выбору константы `Pi_0=+qvecEvecr_0`. Выбрав в качестве точки `A` начало координат `(vecr_0=0)`, получаем `Pi_0=0` и `Pi(vecr)=-qvecEr`.
Важнейшим понятием в учении об электричестве является потенциал. Перепишем выражение для работы сил электростатического поля в виде
`A_(12)=qvecE(vecr_2-vecr_1)=Pi_1-Pi_2=q(varphi_1-varphi_2)`, (1.4.7)
введя потенциал однородного электростатического поля по формуле
`varphi(vecr)=-vecEvecr+varphi_0`, (1.4.8)
`varphi_0` — произвольная постоянная.
Записав (1.4.8) в виде `varphi(vecr)=-(+1)vecEvecr+varphi_0`, можно чисто формально (в согласии с (1.4.5)) трактовать потенциал как потенциальную энергию единичного положительного заряда `(+1)` в электрическом поле. Важно, однако, помнить, что потенциал и потенциальная энергия имеют разные размерности. В силу равенства (1.4.7) и, соответственно,
`varphi=Pi//q`, (1.4.9)
потенциал измеряется в единицах Дж/Кл = В (вольт).
По формуле (1.4.8) найдём ещё изменение потенциала при переходе от одной точки поля к другой — с радиус-векторами `vecr_1` и `vecr_2`:
`Deltavarphi=varphi_2-varphi_1=varphi(vecr_2)-varphi(vecr_1)=-vecE(vecr_2-vecr_1)=-vecEDeltavecr`. (1.4.10)
Заметим, что если перемещение перпендикулярно электрическому полю, `Deltavecr_|_vecE`, то скалярное произведение `vecEDeltavecr=0`, т. е. `Deltavarphi=0`: перемещаясь в плоскости перпендикулярно вектору напряжённости электрического поля `vecE`, переходим от одной точки к другой с таким же потенциалом. О таких плоскостях (в общем случае – о поверхностях) говорят как об эквипотенциальных поверхностях.
А как будет изменяться потенциал при переходе от одной эквипотенциальной плоскости к другой? Рассмотрим перемещение вдоль электрического поля `Deltavecr«||«vecE`. Направим ось `X` параллельно электрическому полю (не обязательно по полю, м. б., и против поля, так что проекция `E_x` вектора `vecE` на ось `X` может иметь любой знак). Согласно основным свойствам скалярного произведения векторов `(vecavecb=|veca|*|vecb|cosalpha=a_xb_x+a_yb_y+a_zb_z)` имеем
`varphi(x)=-E_x+varphi_0`, (1.4.8′)
а для приращения потенциала
`Deltavarphi=varphi_2-varphi_1=varphi(x_2)-varphi(x_1)=-E_x(x_2-x_1)=-E_xDeltax`. (1.4.10′)
Формуле (1.4.10’) можно придать ещё следующий вид. Пусть ось `X` направлена по полю `(E=E_x>0)` и пусть `d=x_2-x_1`. Введём разность потенциалов (напряжение) по формуле `U=varphi_1-varphi_2`. Тогда согласно (1.4.10’) получаем `U=Ed`.
Пример 13
Определить разность потенциалов между двумя параллельными друг другу равномерно заряженными плоскостями, одна из которых заряжена положительно с поверхностной плотностью `sigma_1=+sigma`, а вторая отрицательно `sigma_2=-sigma`. Расстояние между плоскостями равно `d`. Определить также:
1) чему будет равен потенциал 2-ой плоскости, если потенциал 1-ой принять равным нулю?
2) Каким будет потенциал 1-ой плоскости, если за нуль потенциала принять потенциал 2-ой плоскости?
Решение
Направим ось `X` от 1-й плоскости ко 2-й перпендикулярно им обоим и совместим начало координат с 1-й плоскостью. Тогда `U=Ed=sigma/(epsilon_0)d`.
1) Полагая в формуле `varphi(x)=-E_x x+varphi_0`, (1.4.8′) `varphi(0)=0`, получаем `varphi_0=0` и `varphi(d)=-U`.
2) В этом случае положим в (1.4.8′) `varphi(d)=0`, тогда `varphi_0=U` и `varphi(0)=+U`.
Пример 14
Ускоряющее напряжение в электронно-лучевой трубке кинескопа телевизора `U=30` кВ. До какой скорости разгоняются в ней электроны? Какой процент она составляет от скорости света в вакууме `c=3*10^8` м/с. Начальная скорость электрона равна нулю. Масса электрона `m=0,91*10^(-30)` кг.
Решение
Воспользуемся законом сохранения энергии:
`Delta(mv^2//2)=|DeltaPi|=eU`,
откуда получаем `v=sqrt((2eU)/m)~~103000` км/с `~~0,34` с (т. е. составляет `34%` от скорости света).
До сих пор мы рассматривали лишь однородное электростатическое поле. Простейшим примером неоднородного поля является поле точечного заряда. К сожалению, нахождение работы сил даже этого сравнительно простого поля без привлечения высшей математики весьма затруднительно. Поэтому формулу для неё приведём без вывода.
Пусть имеется неподвижный точечный заряд `q` и пусть другой заряд `q_0` перемещается в поле этого заряда. Пусть он переместился из точки `1`, характеризуемой радиус-вектором `vecr_1`, в точку `2` — с радиус-вектором `vecr_2` по, вообще говоря, криволинейной траектории. Можно показать (вывод можно найти в книге `[3]`), что в этом случае работа сил электростатического поля будет равна
`A_(12)=(q_0q)/(4pi epsilon_0r_1) — (q_0q)/(4pi epsilon_0r_2)`, (1.4.11)
где `r_1=|vecr_1|`, `r_2=|vecr_2|`. Далее действуем, как и в случае однородного поля. Если в процессе движения заряда `q_0` никаких других сил, кроме кулоновской силы со стороны заряда `q` не действовало, то по теореме об изменении кинетической энергии имеем:
| `(mv_2^2)/2-(mv_1^2)/2=(q_0q)/(4pi epsilon_0r_1)-(q_0q)/(4pi epsilon_0r_2)`, | |
| или иначе | |
| `(mv_2^2)/2+(q_0q)/(4pi epsilon_0r_2)= (mv_1^2)/2+(q_0q)/(4pi epsilon_0r_1)` | (1.4.12) |
Определяя потенциальную энергию взаимодействия точечных зарядов `q` и `q_0` находящихся на расстоянии `r` друг от друга, формулой
`Pi(r)=(q_0q)/(4pi epsilon_0r)+Pi_0`, (1.4.13)
где `Pi_0` — произвольная постоянная, мы можем придать равенству (1.4.12) вид закона сохранения энергии `K_2+Pi_2=K_1+Pi_1`.
В случае точечных зарядов весьма часто константу `Pi_0` выбирают равной нулю так, чтобы потенциальная энергия взаимодействия двух зарядов стремилась к нулю при разнесении зарядов на бесконечно большое расстояние друг от друга (когда они перестанут «чувствовать» друг друга). В этом случае
`Pi(r)=(q_0q)/(4pi epsilon_0r)`. (1.4.13′)
Пусть в одну и ту же точку поля точечного заряда `q` на расстоянии `r` от него поочерёдно помещаются разные пробные заряды `q_1`, `q_2`, `…`. Энергии этих зарядов будут разными `Pi_1`, `Pi_2`, `…`. Существенно, однако, что отношение этих энергий в величинам пробных зарядов будет одним и тем же
`(Pi_1(r))/(q_1)=(Pi_2(r))/(q_2)=…=q/(4pi epsilon_0r)-=varphi(r)`. (1.4.14)
Последним равенством определяется потенциал `varphi(r)` точечного заряда `q` на расстоянии `r` от него. Заметим, что согласно (1.4.11) потенциал `varphi(r)=q/(4pi epsilon_0r)` равен работе сил электростатического поля заряда `q` при перемещении единичного положительного точечного заряда из точки на расстоянии `r` от заряда `q` на бесконечность. Потенциал, как и потенциальная энергия, определён, вообще говоря, неоднозначно — с точностью до произвольной константы
`varphi(r)=q/(4pi epsilon_0r)+varphi_0`, (1.4.14′)
которую весьма часто выбирают равной нулю с тем, чтобы при удалении от заряда на бесконечно большое расстояние потенциал заряда в этих (бесконечно удалённых точках) стремился к нулю.
Согласно формуле (1.4.14′) потенциал точечного заряда одинаков во всех точках, равноудалённых от него. Это означает, что эквипотенциальными поверхностями в данном случае будут концентрические сферы. Как и в случае однородного поля, в каждой точке поля напряжённость перпендикулярна эквипотенциальной поверхности.
Если электростатическое поле создаётся несколькими зарядами `q_1,q_2,…`, потенциал в произвольной точке поля равен сумме потенциалов, создаваемых каждым из зарядов в той точке:
`varphi=varphi_1+varphi_2+…`, (1.4.15)
что, как и в случае напряжённостей полей, называют принципом суперпозиции. Важно, что напряжённости полей надо складывать векторно, а потенциалы — алгебраически (т. е. все же с учётом знаков).
Пример 15
Если воздушный шарик радиусом `R=10` см потереть о шерсть, о мех или о волосы, то он приобретёт довольно большой отрицательный заряд – порядка `q=0,1` мкКл. Каким будет при этом потенциал шарика?
Решение
Поле вне шара совпадает с полем точечного заряда. Потенциал шара будет равен
`varphi=1/(4pi epsilon_0) q/R=9000` В,
т. е. почти `10` киловольт (!). Возникает естественный вопрос: не слишком много вольт мы здесь получили? Нет ли ошибки в нашей оценке? Нет, мы не ошибаемся. Несмотря на столь внушительный потенциал, шар будет обладать весьма незначительной энергией. Оценить энергию воздушного шарика можно по формуле `W=(1//2)qvarphi`, которую мы приведём без вывода, что даёт `W~~10,5*10^(-3)` Дж, поэтому все эти `9` тысяч вольт реальной опасности не представляют.
Пример 16
В случае движения отдельных элементарных частиц (электронов, протонов) удобной единицей измерения энергии является электрон-вольт (эВ). Так называют энергию, которую приобретает частица с зарядом, равным элементарному электрическому заряду, пройдя разность потенциалов в `1` вольт. Энергия электрона в атоме водорода равна `W=-13,6` эВ. Считая, что электрон в атоме водорода движется по круговой орбите, найти радиус этой орбиты.
Решение
Энергия электрона складывается из кинетической и потенциальной: `W=(mv^2)/2-(e^2)/(4pi epsilon_0r)`. Запишем ещё 2-й закон Ньютона для движения электрона в поле протона: `(mv^2)/r=(e^2)/(4pi epsilon_0r^2)`, откуда получаем `(mv^2)/2=1/2 (e^2)/(4pi epsilon_0r)` и `W=-1/2 (e^2)/(4pi epsilon_0r)`. Решая это уравнение относительно `r`, после подстановки числовых значений находим `r=0,53*10^(-10)` м.
Два основных объекта нашего дальнейшего изучения это – проводники и диэлектрики в электрическом поле, а также электрические поля в вакууме в их присутствии. Считается, что в проводниках имеется большое число подвижных носителей заряда (способных свободно перемещаться в пределах проводника). В диэлектриках, напротив, считается, что таких подвижных зарядов практически нет (их число пренебрежимо мало).
Потенциал
Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом
данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Литература
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 228-233.
- Жилко, В. В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) /В. В. Жилко, Л. Г. Маркович. — 2-е изд., исправленное. — Минск: Нар. асвета, 2008. — С. 86-95.
Как определить знак потенциала
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
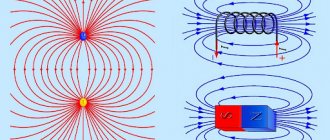
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ — точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком «минус». Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак «+», работа имеет знак «-«.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Силы и их действие на заряженную частицу
На заряженный электрон, воздействует сила с некоторым ускорением, заставляя его перемещаться все быстрее и быстрее. Этой силой совершается работа по передвижению электрона.
Силовые линии – это воображаемые очертания, которые возникают вокруг зарядов (определяется электрическим полем), и если мы поместим какой-либо заряд в эту область, он испытает силу.
Свойства силовых линий:
- путешествуют с севера на юг;
- не имеют взаимных пересечений.
Почему у двух силовых линий не возникает пересечений? Потому что не бывает этого в реальной жизни. То, о чём говорится, является физической моделью и не более. Физики изобрели её для описания поведения и характеристик электрического поля. Модель очень хороша при этом. Но помня, что это всего лишь модель, мы должны знать о том, для чего такие линии нужны.
Силовые линии демонстрируют:
- направления электрических полей;
- напряженность. Чем ближе линии, тем больше сила поля и наоборот.
Если нарисованные силовые линии нашей модели пересекутся, расстояние меж ними станет бесконечно малыми. Из-за силы поля, как формы энергии, и из-за фундаментальных законов физики это невозможно.
4.Понятие о циркуляции
Пусть в некоторой области пространства существует векторное поле .
| Циркуляцией вектора по произвольному замкнутому контуру L называется следующий криволинейный интеграл: |
Здесь — единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.
Существует соглашение, что положительное направление обхода контура (направление ) выбирается таким, чтобы область, охваченная контуром, оставалась при обходе слева.
Напомним, вкратце, как можно “сконструировать” криволинейный интеграл. Для этого нужно выбрать точку на контуре, показать в ней вектор , в этой же точке показать единичный вектор касательной, вычислить скалярное произведение , разбить контур на малые элементы, длину элемента обозначить , вычислить произведение ; проделать это для всех элементов контура; произвести суммирование результатов, устремляя элемент длины контура к нулю — перейти от суммирования к интегрированию.
Так же, как и поток, циркуляция является ещё одной характеристикой свойств векторного поля. А именно, циркуляция характеризует степень завихренности векторного поля.
Пример:
если в качестве «измерителя» циркуляции поля скоростей жидкости можно взять турбинку, то если она вращается, циркуляция не равна нулю.
Циркуляция
– это интегральная характеристика поля.
План:
| 1.Работа электрического поля. |
| 2.Работа в поле точечного заряда. |
| 3.Теорема о циркуляции. |
| 4.Понятие о циркуляции. |
| 5.Понятие ротора. |
| 6.Формула Стокса. |
| 7.Выражение для ротора в декартовой системе координат. |
| 8.Циркуляция и ротор в электростатике. |
| 9.Потенциальная энергия. |
| 10.Разность потенциалов. |
| 11.Единица разности потенциалов. |
| 12.Потенциал точечного заряда. |
5.Понятие ротора
Поле по своей структуре может быть достаточно неоднородным. Циркуляция же не дает детальной характеристики поля. Следовательно, начнем стягивать контур интегрирования к какой-либо точке М
(уменьшать турбину). Циркуляция при этом будет стремиться к нулю, но и площадь, охваченная контуром, также будет стремиться к нулю. А их отношение дает конечное число.
Турбину можно ориентировать в пространстве тремя независимыми способами. Следовательно, таким способом можно получить 3 независимых числа, а три числа – это вектор, следовательно, образуется векторная характеристика поля, которая и называется ротором.
Ротор
– это локальная или дифференциальная характеристика.