Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
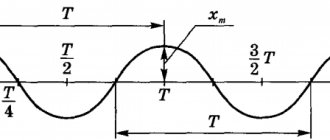
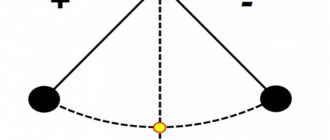
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.
За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, т. е. для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:
.
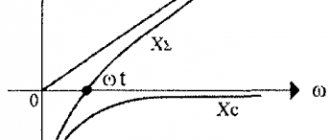
В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:
.
Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Период и частота переменного тока
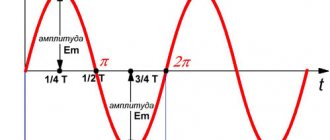
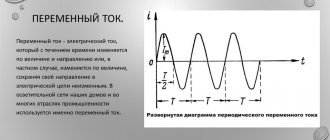
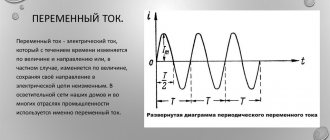
Время, в течение которого совершается одно полное изменение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания переменного тока (рисунок 1).
Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.
Период выражают в секундах и обозначают буквой Т.
Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.
1 мс =0,001сек =10 -3 сек.
1 мкс=0,001 мс = 0,000001сек =10 -6 сек.
Число полных изменений ЭДС или число оборотов радиуса-вектора, то есть иначе говоря, число полных циклов колебаний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока.
Частота обозначается буквой f и выражается в периодах в секунду или в герцах.
Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.
1000 Гц = 10 3 Гц = 1 кГц;
1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;
1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;
Чем быстрее происходит изменение ЭДС, то есть чем быстрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.
Математическая связь между периодом и частотой переменного тока и напряжения выражается формулами
Например, если частота тока равна 50 Гц, то период будет равен:
Т = 1/f = 1/50 = 0,02 сек.
И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:
f = 1/T=1/0,02 = 100/2 = 50 Гц
Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.
Частоты от 20 до 20 000 Гц называются звуковыми частотами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие высокие частоты называются радиочастотами или колебаниями высокой частоты.
Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.
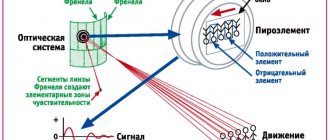
Значение Cos φ
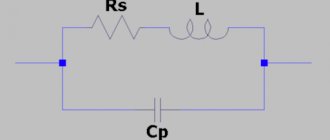
Cos φ в практической электротехнике имеет очень важное значение. Реальные нагрузки, типа электромоторов и трансформаторов, имеют большую индуктивную составляющую сопротивления, то есть, фактически, представляют собой цепи RL
Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P).
Из формулы видно, что чем меньше Cos φ (Чем больше угол сдвига фаз), тем меньшую часть активная мощность составляет от полной мощности .
Только активная мощность является полезной, если источник затрачивает полную мощность, а от нагрузки мы можем получить только активную мощность, значит, Cos φ имеет смысл электротехнического КПД или коэффициента мощности.
В идеале источник должен отдавать такую мощность, которую будет потреблять нагрузка. Реальные устройства неизбежно содержат индуктивности (катушки, обмотки, и т.п.), значит, источник вынужден отдавать полную мощность, которая значительно больше, активной.
Проектирование устройств и электрических цепей должно иметь целью получить значение Cos φ
как можно ближе к единице, то есть влияние индуктивности надо свести к минимуму. Плохие значения
Cos φ
приводят к большим неоправданным затратам электроэнергии.
Угловая (циклическая) частота переменного тока.
Скорость вращения радиуса-вектора, т. е. изменение величины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (омега). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.
Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.
Рисунок 2. Радиан.
1рад = 360°/2
Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в течение одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его конец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .
? = 6,28*f = 2f
Фаза переменного тока.
Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза показывает, убывает ли ЭДС или возрастает.
Рисунок 3. Фаза переменного тока.
Полный оборот радиуса-вектора равен 360°. С началом нового оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следовательно, все фазы ЭДС будут повторяться в прежнем порядке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обоих этих случаях радиус-вектор занимает одинаковое положение, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Как вычислить сечение многожильного провода
Многожильный провод, чем он отличается от одножильного? В принципе ничем, несколько одножильных проводов свитые вместе, а поэтому вычислить сечение одножильного провода и помножив на количество проводов получим сечение многожильного провода. Рассмотрим на примере: Имеется в распоряжении многожильный провод, сплетенный из 12 жил, диаметр одножильного провода 0,4 мм. Рассчитываем сечение жилы: 0,4мм х 0,4мм х 0,785 = 0,1256, округляем и получаем 0,126 мм 2. Сечение многожильного провода 0,126 мм 2 х 12 = 1,5 мм 2. Заходим в таблицу и определяем, что такой провод способен выдержит ток 8 Ампер.
При желании можно определить сечение многожильного провода, замерив общий диаметр кабеля, так как между проводниками имеется пространство, то с помощью коэффициента 0,91 мы приблизительно рассчитаем общее сечение, что нам будет достаточно этой точности. К примеру, замерив диаметр многожильного провода, мы получили 5 мм, рассчитываем: 5,0 мм х 5,0 мм х 0,785 = 19,625 мм 2, далее 19,625 мм 2 умножаем на 0,91 получаем 17,85 2. По таблице видим, что ток на который рассчитан провод более 63 А.
| Онлайн калькулятор для определения сечения многожильного провода |
| Введите диаметр одной жилы, мм: |
| Количество жил в проводе: |
Вот еще один простой калькулятор расчета. Для вычисления потребляемого тока применяем известную формулу, для этого делим мощность прибора (Вт) на напряжение (вольт) , после деления результат получается в амперах. Чайник потребляет 1200 Вт от сети 220 вольт, вычисляем 1200 дели на 220 получаем ток 5,45 А.
| Онлайн калькулятор для определения величины тока по потребляемой мощности |
| Потребляемая мощность, Вт: |
| Напряжение питания, В: |
Для вычисления необходимо вписать оба значения, иначе программа не поймет и выдаст соответствующее сообщение.
Расчет сопротивления для подключения светодиодов
Иногда требуется включить светодиодный индикатор в схему, но напряжение на данном участке больше требуемого. Напомним, что для загорание обычного светодиода требуется напряжение источника постоянного тока величиной 1,5 — 2 вольта и ток потребляемый им составляет 10 — 20 ма (для загорания и меньше в пределах 5 ма), напряжение и потребляемый ток зависят от разных характеристик, в том числе и от цвета излучаемым светодиодом и от его отличительных характеристики — имеется класс ярких светодиодов с малым потреблением тока.
Расчет производится по формуле:
ΔU=Uгасящее=Uпитания–Uсветодиода, т.е. ΔU разница напряжения между источником питания и значением величины рабочего напряжения данного светодиода. Необходимо представлять себе, что если вы хотите включить индикацию напряжения, к примеру 220 вольт, то потребуется погасить на резисторе 218 вольт, т.е. 220-2=218, для этого потребуется резистором номиналом 15 кОм и мощностью рассеивания 3,5 Вт, в данном случае лучше составить из трех резисторов по 5,1 кОм, или четырех резисторов по 3,9 кОм (Ряд E24). Где U в вольтах, I в амперах, R в омах.
Характеристика колебаний
Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.
Циклическая частота характеризует скорость изменения фазы колебаний.
Начальное состояние колебательной системы характеризует начальная фаза
Амплитуда колебаний A — это наибольшее смещение из положения равновесия
Период T — это промежуток времени, в течение которого точка выполняет одно полное колебание.
Частота колебаний — это число полных колебаний в единицу времени t.
Частота, циклическая частота и период колебаний соотносятся как
Виды колебаний
Колебания, которые происходят в замкнутых системах называются свободными или собственными колебаниями. Колебания, которые происходят под действием внешних сил, называют вынужденными. Встречаются также автоколебания (вынуждаются автоматически).
Если рассматривать колебания согласно изменяющихся характеристик (амплитуда, частота, период и др.), то их можно разделить на гармонические, затухающие, нарастающие (а также пилообразные, прямоугольные, сложные).
При свободных колебаниях в реальных системах всегда происходят потери энергии. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, и через некоторое время колебания прекращаются. Очевидно, что чем больше силы сопротивления движению, тем быстрее прекращаются колебания.
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости. Пока пружина не деформирована, сила упругости на тело не действует.
| Формула периода колебания пружинного маятника T — период [с] m — масса маятника [кг] k — жесткость пружины [Н/м] π = 3,14 |
Вынужденные колебания. Резонанс
Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.
Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом.
Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Примеры резонанса
Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать
Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.
В музыкальных инструментах роль резонаторов выполняют части их корпусов. Человек также имеет собственный резонатор — это полость рта, усиливающая издаваемые звуки.
Явление резонанса необходимо учитывать на практике. В одних явлениях он может быть полезен, в других — вреден. Резонансные явления могут вызывать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США.
Явление резонанса используется, когда с помощью небольшой силы необходимо получить большое увеличение амплитуды колебаний. Например, тяжелый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.
Колебания и их амплитуда
Повторяющиеся движения или процессы называют колебаниями
.
В зависимости от природы колебания могут быть механическими, электромагнитными, звуковыми и др. Разные виды колебаний описывают с помощью одинаковых уравнений и при этом используют одинаковые характеристики.
Колебания называют свободными
(иди собственными), если они происходят за счет энергии, которая получена колебательной системой один раз и в дальнейшем внешних воздействий на эту систему нет.
Самым простым видом колебаний являются гармонические колебания.
Гармоническими колебаниями
называют такие колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса..
Пусть происходят гармонические колебания некоторого параметра $s$, тогда эти колебания можно описать при помощи следующего уравнения:
где $A=s_ $ — амплитуда колебаний; $ _0$ — циклическая (круговая) частота колебаний; $varphi $ — начальная фаза колебаний (фаза при $t=0$); $( _0t+varphi )$ — фаза колебаний.
Амплитудой называют максимальной значение величины, колебания которой рассматривают. Так как косинус (как и синус) изменяется в пределах от единицы до минус единицы, то величина $s$ находится в пределах $-Ale sle $+A.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
| Формула периода колебания математического маятника T — период [с] l — длина нити [м] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2 π = 3,14 |