Oscillation period.
The period of oscillation is the shortest period of time through which a system oscillating returns again to the same state in which it was at the initial moment of time, chosen arbitrarily.
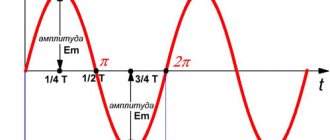
In other words, the period of oscillation (T) is the time during which one complete oscillation occurs. For example, in the figure below, this is the time during which the pendulum bob moves from the extreme right point through the equilibrium point O to the extreme left point and back through point O again to the extreme right.
Over a full period of oscillation, the body thus travels a path equal to four amplitudes. The period of oscillation is measured in units of time - seconds, minutes, etc. The period of oscillation can be determined from a well-known graph of oscillations (see figure below).
The concept of “oscillation period,” strictly speaking, is valid only when the values of the oscillating quantity are exactly repeated after a certain period of time, that is, for harmonic oscillations. However, this concept also applies to cases of approximately repeating quantities, for example, for damped oscillations .
Oscillation frequency.
Oscillation frequency is the number of oscillations performed per unit of time, for example, 1 s.
The SI unit of frequency is named hertz (Hz) in honor of the German physicist G. Hertz (1857-1894). If the oscillation frequency (v) is 1 Hz, this means that one oscillation occurs every second. The frequency and period of oscillations are related by the relations:
.
cyclic or circular frequency is also used . It is related to the usual frequency v and the oscillation period T by the relations:
.
Cyclic frequency is the number of oscillations completed in 2π seconds.
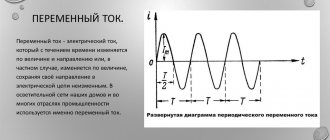
AC period and frequency
The time during which one complete change in the emf occurs, that is, one cycle of oscillation or one full revolution of the radius vector, is called the period of alternating current oscillation (Figure 1).
Figure 1. Period and amplitude of a sinusoidal oscillation. Period is the time of one oscillation; Amplitude is its greatest instantaneous value.
The period is expressed in seconds and denoted by the letter T.
Smaller units of measurement of period are also used: millisecond (ms) - one thousandth of a second and microsecond (μs) - one millionth of a second.
1 ms = 0.001 sec = 10 -3 sec.
1 μs = 0.001 ms = 0.000001 sec = 10 -6 sec.
The number of complete changes in the emf or the number of revolutions of the radius vector, that is, in other words, the number of complete cycles of oscillations performed by alternating current within one second, is called alternating current oscillation frequency .
Frequency is designated by the letter f and is expressed in cycles per second or hertz.
One thousand hertz is called a kilohertz (kHz), and a million hertz is called a megahertz (MHz). There is also a unit of gigahertz (GHz) equal to one thousand megahertz.
1000 Hz = 10 3 Hz = 1 kHz;
1000 000 Hz = 10 6 Hz = 1000 kHz = 1 MHz;
1000 000 000 Hz = 10 9 Hz = 1000 000 kHz = 1000 MHz = 1 GHz;
The faster the EMF changes, that is, the faster the radius vector rotates, the shorter the oscillation period. The faster the radius vector rotates, the higher the frequency. Thus, the frequency and period of alternating current are quantities inversely proportional to each other. The larger one of them, the smaller the other.
The mathematical relationship between the period and frequency of alternating current and voltage is expressed by the formulas
For example, if the current frequency is 50 Hz, then the period will be equal to:
T = 1/f = 1/50 = 0.02 sec.
And vice versa, if it is known that the period of the current is 0.02 sec, (T = 0.02 sec.), then the frequency will be equal to:
f = 1/T=1/0.02 = 100/2 = 50 Hz
The frequency of alternating current used for lighting and industrial purposes is exactly 50 Hz.
Frequencies between 20 and 20,000 Hz are called audio frequencies. Currents in radio station antennas oscillate with frequencies up to 1,500,000,000 Hz or, in other words, up to 1,500 MHz or 1.5 GHz. These high frequencies are called radio frequencies or high frequency vibrations.
Finally, currents in the antennas of radar stations, satellite communication stations, and other special systems (for example, GLANASS, GPS) fluctuate with frequencies of up to 40,000 MHz (40 GHz) and higher.
Cosφ value
Cos φ is very important in practical electrical engineering. Real loads, such as electric motors and transformers, have a large inductive component of resistance, that is, in fact, they represent RL circuits
For such circuits, there is inevitably a phase shift, which leads to the fact that the apparent power S significantly exceeds the active power (P).
From the formula it is clear that the smaller Cos φ (the larger the phase angle), the smaller the active power is from the total power.
Only active power is useful if the source expends full power, and we can only get active power from the load, which means Cos φ has the meaning of electrical efficiency or power factor.
Ideally, the source should supply the same amount of power that the load will consume. Real devices inevitably contain inductance (coils, windings, etc.), which means that the source is forced to deliver full power, which is much greater, to the active one.
The design of devices and electrical circuits should aim to obtain the value of Cos φ
as close to unity as possible, that is, the influence of inductance should be minimized.
Poor Cos φ
lead to large unjustified energy costs.
Angular (cyclic) frequency of alternating current.
The rotation speed of the radius vector, i.e., the change in the rotation angle within one second, is called the angular (cyclic) frequency of alternating current and is denoted by the Greek letter ? (omega). The angle of rotation of the radius vector at any given moment relative to its initial position is usually measured not in degrees, but in special units - radians.
A radian is the angular value of an arc of a circle, the length of which is equal to the radius of this circle (Figure 2). The entire circle that makes up 360° is equal to 6.28 radians, that is, 2.
Figure 2. Radian.
1rad = 360°/2
Consequently, the end of the radius vector during one period covers a path equal to 6.28 radians (2). Since within one second the radius vector makes a number of revolutions equal to the frequency of the alternating current f, then in one second its end covers a path equal to 6.28 * f radians. This expression characterizing the rotation speed of the radius vector will be the angular frequency of the alternating current - ? .
? = 6.28*f = 2f
AC phase.
The angle of rotation of the radius vector at any given instant relative to its initial position is called the phase of the alternating current . The phase characterizes the magnitude of the EMF (or current) at a given instant or, as they say, the instantaneous value of the EMF, its direction in the circuit and the direction of its change; phase indicates whether the emf is decreasing or increasing.
Figure 3. AC phase.
A full rotation of the radius vector is 360°. With the beginning of a new revolution of the radius vector, the EMF changes in the same order as during the first revolution. Consequently, all phases of the EMF will be repeated in the same order. For example, the phase of the EMF when the radius vector is rotated by an angle of 370° will be the same as when rotated by 10°. In both of these cases, the radius vector occupies the same position, and, therefore, the instantaneous values of the emf will be the same in phase in both of these cases.
DID YOU LIKE THE ARTICLE? SHARE WITH YOUR FRIENDS ON SOCIAL NETWORKS!
How to calculate the cross-section of a stranded wire
How is stranded wire different from solid wire? In principle, nothing, several single-core wires twisted together, and therefore calculate the cross-section of a single-core wire and multiply by the number of wires to obtain the cross-section of a multi-core wire. Let's look at an example: We have at our disposal a stranded wire woven from 12 cores, the diameter of the single-core wire is 0.4 mm. We calculate the cross-section of the core: 0.4 mm x 0.4 mm x 0.785 = 0.1256, round it up and get 0.126 mm 2. Cross-section of a stranded wire 0.126 mm 2 x 12 = 1.5 mm 2. We go into the table and determine that such a wire is capable will withstand a current of 8 Amps.
If desired, you can determine the cross-section of a stranded wire by measuring the total diameter of the cable, since there is space between the conductors, then using a coefficient of 0.91 we will approximately calculate the total cross-section, which will be enough for us with this accuracy. For example, having measured the diameter of a stranded wire, we got 5 mm, we calculate: 5.0 mm x 5.0 mm x 0.785 = 19.625 mm 2, then multiply 19.625 mm 2 by 0.91, we get 17.85 2. From the table we see, that the current for which the wire is designed is more than 63 A.
| Online calculator for determining the cross-section of a stranded wire |
| Enter the diameter of one core, mm: |
| Number of cores in the wire: |
Here is another simple calculation calculator. To calculate the current consumption, we use the well-known formula; to do this, we divide the power of the device (W) by the voltage (volts), after dividing the result is obtained in amperes. The kettle consumes 1200 W from a 220 volt network, calculating 1200 divided by 220 we get a current of 5.45 A.
| Online calculator for determining the current value based on power consumption |
| Power consumption, W: |
| Supply voltage, V: |
To calculate, you must enter both values, otherwise the program will not understand and will display a corresponding message.
Calculation of resistance for connecting LEDs
Sometimes it is necessary to include an LED indicator in the circuit, but the voltage in this area is higher than required. Let us recall that for the lighting of a conventional LED, a voltage of a direct current source of 1.5 - 2 volts is required and the current consumed by it is 10 - 20 mA (for lighting and less within 5 mA), the voltage and current consumption depend on various characteristics, including including the color emitted by the LED and its distinctive characteristics - there is a class of bright LEDs with low current consumption.
The calculation is made using the formula:
ΔU=Uquenching=Upower–ULED, i.e. ΔU is the voltage difference between the power source and the operating voltage value of a given LED. You need to imagine that if you want to turn on the voltage indication, for example 220 volts, then you will need to turn off 218 volts at the resistor, i.e. 220-2=218, this will require a resistor with a nominal value of 15 kOhm and a dissipation power of 3.5 W, in this case it is better to make up three resistors of 5.1 kOhm, or four resistors of 3.9 kOhm (Series E24). Where U is in volts, I is in amperes, R is in ohms.
Oscillation characteristics
The phase determines the state of the system, namely coordinate, speed, acceleration, energy, etc.
The cyclic frequency characterizes the rate of change in the phase of oscillations.
The initial state of the oscillatory system is characterized by the initial phase
Oscillation amplitude A is the largest displacement from the equilibrium position
Period T is the period of time during which the point performs one complete oscillation.
Oscillation frequency is the number of complete oscillations per unit time t.
Frequency, cyclic frequency and period of oscillation are related as
Types of vibrations
Oscillations that occur in closed systems are called free or natural oscillations. Oscillations that occur under the influence of external forces are called forced. There are also self-oscillations (forced automatically).
If we consider oscillations according to changing characteristics (amplitude, frequency, period, etc.), then they can be divided into harmonic, damped, increasing (as well as sawtooth, rectangular, complex).
During free oscillations in real systems, energy losses always occur. Mechanical energy is spent, for example, on performing work to overcome air resistance forces. Under the influence of friction, the amplitude of oscillations decreases, and after some time the oscillations stop. Obviously, the greater the force of resistance to movement, the faster the oscillations stop.
Spring pendulum
A spring pendulum is a mass attached to a spring whose mass can be neglected.
In a spring pendulum, oscillations occur under the action of elastic force. While the spring is not deformed, the elastic force does not act on the body.
| Formula for the period of oscillation of a spring pendulum T - period [s] m—pendulum mass [kg] k - spring stiffness [N/m] π = 3.14 |
Forced vibrations. Resonance
Forced oscillations are undamped. Therefore, it is necessary to replenish energy losses for each oscillation period. To do this, it is necessary to influence the oscillating body with a periodically changing force. Forced vibrations occur with a frequency equal to the frequency of changes in the external force.
The amplitude of forced mechanical vibrations reaches its greatest value if the frequency of the driving force coincides with the frequency of the oscillatory system. This phenomenon is called resonance .
For example, if we periodically pull the cord in time with its own vibrations, we will notice an increase in the amplitude of its vibrations.
Self-oscillations
Sometimes a forced oscillation does not need any external influence to happen. There are systems in which this external influence arises itself due to the ability to regulate the supply of energy from a constant source.
A self-oscillating system has three important components:
- the oscillatory system itself
- energy source
- feedback device providing communication between the source and the system
A cuckoo clock is an example of a self-oscillating system. The weight on the string (chain) tends to rotate the gear wheel (ratchet). When the pendulum oscillates, the anchor catches on the tooth and the rotation stops.
But as a result, the pendulum receives a push, compensating for the loss of energy due to friction. The potential energy of the weight, which gradually lowers, is spent on maintaining undamped oscillations.
Examples of resonance
If you move a wet finger along the edge of a glass, the glass will make ringing sounds. Although it is not noticeable, the finger moves intermittently and transfers energy to the glass in short bursts, causing the glass to vibrate
The walls of the glass also begin to vibrate if a sound wave with a frequency equal to its own is directed at it. If the amplitude becomes very large, the glass may even break. Due to resonance, when F.I. Chaliapin sang, the crystal pendants of the chandeliers trembled (resonated). The occurrence of resonance can also be observed in the bathroom. If you softly sing sounds of different frequencies, a resonance will arise at one of the frequencies.
In musical instruments, the role of resonators is performed by parts of their bodies. A person also has his own resonator - this is the oral cavity, which amplifies the sounds made.
The phenomenon of resonance must be taken into account in practice. In some cases it can be useful, in others it can be harmful. Resonance phenomena can cause irreversible damage in various mechanical systems, such as poorly designed bridges. Thus, in 1905, the Egyptian Bridge in St. Petersburg collapsed when a horse squadron was passing across it, and in 1940, the Tacoma Bridge in the USA collapsed.
The phenomenon of resonance is used when, with the help of a small force, it is necessary to obtain a large increase in the amplitude of vibrations. For example, the heavy tongue of a large bell can be swung by applying a relatively small force with a frequency equal to the natural frequency of the bell.
Oscillations and their amplitude
Repeated movements or processes are called oscillations
.
Depending on the nature, vibrations can be mechanical, electromagnetic, sound, etc. Different types of vibrations are described using the same equations and the same characteristics are used.
Vibrations are called free
(go own), if they occur due to the energy that is received by the oscillatory system once and there are no further external influences on this system.
The simplest type of vibration is harmonic vibration.
Harmonic vibrations
are called such oscillations in which the oscillating quantity changes over time according to the law of sine or cosine.
Let harmonic oscillations of some parameter $s$ occur, then these oscillations can be described using the following equation:
where $A=s_ $ is the amplitude of oscillations; $ _0$ — cyclic (circular) frequency of oscillations; $varphi $ — initial phase of oscillations (phase at $t=0$); $( _0t+varphi )$ is the oscillation phase.
Amplitude is the maximum value of the quantity whose fluctuations are being considered. Since the cosine (like the sine) varies from one to minus one, the value $s$ is within the range $-Ale sle $+A.
Math pendulum
A mathematical pendulum is an excellent example of harmonic oscillations. If we hang a ball on a thread, then it will not yet be a mathematical pendulum - for now it is only a physical one.
This pendulum will become mathematical if the dimensions of the ball are much smaller than the length of the thread (then these dimensions can be neglected and the ball can be considered as a material point), the stretching of the thread is very small, and the mass of the thread is many times less than the mass of the ball.
A mathematical pendulum is a system that consists of a material point of mass m and a weightless inextensible thread of length l, on which the material point is suspended, and which is in the field of gravity (or other forces).
The period of small oscillations of a mathematical pendulum in the Earth's gravity field is determined by the formula:
| Formula for the period of oscillation of a mathematical pendulum T - period [s] l — thread length [m] g—gravitational acceleration [m/s2] On planet Earth g = 9.8 m/s2 π = 3.14 |