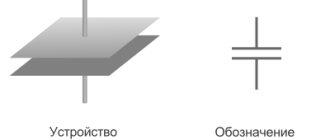
Что такое конденсатор
Конденсатор или как в народе говорят — «кондер», образуются от латинского «condensatus», что означает как «уплотненный, сгущенный». Он представляет из себя пассивный радиоэлемент, который обладает таким свойством, как сохранение электрического заряда на своих обкладках, если, конечно, перед этим его зарядить каким-нибудь источником питания.
Грубо говоря, конденсатор можно рассматривать как батарейку или аккумулятор электрической энергии. Но вся разница в том, что аккумулятор или батарейка имеют в своем составе источник ЭДС, тогда как конденсатор лишен этого внутреннего источника.
Из чего состоит конденсатор
Любой конденсатор состоит из двух или более металлических обкладок, которые не соприкасаются друг с другом. Для более полного понимания, как все это устроено в конденсаторе, давайте представим себе блин.
намажем его сгущенкой
и сверху положим точно такой же блин
Должно выполняться условие: эти два блина не должны прикасаться друг с другом. То есть верхний блин должен лежать на сгущенке и не прикасаться с нижним блином. Тут, думаю, все понятно. Перед вами типичный «блинный конденсатор» :-). Вот таким образом устроены все конденсаторы, только вместо блинов используются тонкие металлические пластины, а вместо сгущенки различный диэлектрик. В качестве диэлектрика может быть воздух, бумага, электролит, слюда, керамика, и так далее. К каждой металлической пластине подсоединены проводки — это выводы конденсатора.
Схематически все это выглядит примерно вот так.
Как вы могли заметить, из-за диэлектрика конденсатор не может проводить ток. Но это относиться только к постоянному току. Переменный ток конденсатор пропускает через себя без проблем с небольшим сопротивлением, номинал которого зависит от частоты тока и емкости самого конденсатора.
Определение заряда
Определить, заряжен ли проводник, можно специальным измерительным прибором. К примеру, сделать это можно при помощи индикаторной отвертки. При разряде избыточные виды электронов, имеющих левую пластину, будут перемещены через некоторое время по проводам к правой части пластины, то есть они будут смещены к местам, где их недостаточно.
Вам это будет интересно Особенности проекта электроснабжения
Обратите внимание! Когда число электронов будет одинаковым, то разряд прекратится и проводная энергия вместе с сопротивлением исчезнет.
Использование измерительного оборудования для определения конденсаторного заряда
Где и для чего используются
Как уже говорили, сложно найти схему без конденсаторов. Их применяют для решения самых разных задач:
- Для сглаживания скачков сетевого напряжения. В таком случае их ставят на входе устройств, перед микросхемами, которые требовательны к параметрам питания.
- Для стабилизации выходного напряжения блоков питания. В таком случае надо искать их перед выходом. Часто можно увидеть электролитические цилиндрические конденсаторы
- Датчик прикосновения (тач-пады). В таких устройствах оной из «пластин» конденсаторов является человек. Вернее, его палец. Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения.
- Для задания необходимого ритма работы. Время заряда конденсаторов разной ёмкости отличается. При этом цикл заряд/разряд конденсатора остаётся величиной постоянной. Это и используется в цепях, где надо задавать определённый ритм работы.
- Ячейки памяти. Память компьютеров, телефонов и других устройств — это огромное количество маленьких конденсаторов. Если он заряжен — это единица, разряжен — ноль.
- Есть стартовые конденсаторы, которые помогают «разогнать» двигатель. Они накапливают заряд, потом резко его отдают, создавая требуемый «толчок» для разгона мотора.
- В фотовспышках. Принцип тот же. Сначала накапливается заряд, затем выдаётся, но преобразуется в свет.
Конденсаторы встречаются часто и область их применения широка. Но надо знать как правильно их подключить.
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
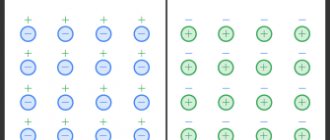
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Сначала лучше проверить
Для начала этот элемент нужно обесточить. Понятно, что не надо именного его лишать источника питания. Достаточно отключить электроприбор и отсоединить вилку от розетки. Если подойти к этому вопросу кардинально, то для безопасности можно на распредщитке отключить все автоматические выключатели, отвечающие за подачу электричества в помещение.
Теперь нам нужен специальный прибор — мультиметр, чтобы узнать заряжен ли конденсатор.
- Выбираем режим для измерения напряжения DC (постоянного тока).
- Ручку прибора выставляем на максимальный уровень замера напряжения.
- Щупы мультиметра подсоединяем к контактам электронного компонента. Из него, как правило, выступают два стержня. Вот именно к ним и нужно присоединить оба щупа детектора. Прижимать нужно достаточно плотно, чтобы на дисплее прибора появились цифровые показания. Нет никакой разницы, какой щуп подводить к какому контакту. Полученное значение получится одинаковым в обоих случаях.
Нам нужно понять какое напряжение на выводах элемента. В зависимости от показаний выбирается и способ разрядки:
- Если показания меньше 10 вольт необходимости в разрядке нет.
- Если на дисплее замеры в пределах 10–99 вольт, разрядить можно отверткой.
- Если значения от 100 вольт и выше рекомендуется применить разрядное устройство.
Важно! Не прикасайтесь голыми руками к выводам — остаточное напряжение может нанести удар током или ожог.
Емкость и энергия конденсатора.
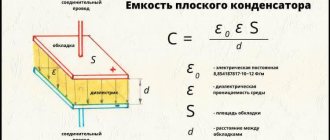
Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:
C = frac{q}{Deltavarphi} = frac{q}{U}
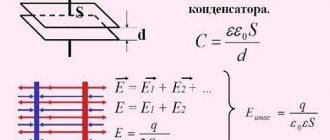
Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:
Будет интересно➡ Кто изобрел электричество? История развития электричества — кто и в каком году его открыл
U = Ed = frac{qd}{varepsilon_0thinspacevarepsilon S}
Здесь у нас d — это расстояние между пластинами конденсатора, а q — заряд конденсатора. Подставим эту формулу в выражение для емкости:
C = frac{qvarepsilon_0thinspacevarepsilon S}{qd} = frac{varepsilon_0thinspacevarepsilon S}{d}
Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить varepsilon = 1.
Для запасенной энергии конденсатора справедливы следующие выражения:
W = frac{CU^2}{2} = frac{qU}{2} = frac{q^2}{2C}
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!
ЭКСПЕРИМЕНТ 2
Изучение зависимости от времени количества тепла, выделившегося на нагрузке при разряде конденсатора
- Выполняя действия, аналогичные описанным в эксперименте 1, зарядите конденсатор до напряжения, соответствующего суммарному значению э.д.с. для вашего варианта.
- Нажмите кнопку «Стоп» и отключите ключ К.
- Проведите 5-ти секундный процесс частичного разряда конденсатора через подключённые лампы. Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора.
- Запишите показания амперметра в таблицу 4 и вновь зарядите конденсатор до первоначального напряжения.
- Последовательно увеличивая длительность процесса разрядки конденсатора на 5 с, проделайте эти опыты до времени разрядки, соответствующему полному исчезновению заряда на конденсаторе. (Напряжение на конденсаторе и ток разрядки через лампы должен быть близким к нулю). Результаты измерений тока разрядки запишите в соответствующие ячейки таблицы 4.
Таблица 4. Результаты измерений и расчетов
| Время разрядки t, с | 5 | 10 | 15 | 20 | 5n | |
| Ток разряда I через t с, А | ||||||
| Кол-во тепла Q за t с, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- Для каждого времени разрядки вычислите по формуле (4) количество тепла, выделившегося на шести лампах и запишите эти значения в соответствующие ячейки третьей строки табл.4. Полезный совет: для расчёта Q воспользуйтесь программой MS Exсel.
- Постройте график зависимости количества выделившегося тепла Q к данному моменту времени от длительности процесса разрядки конденсатора t.
- Сравните рассчитанное количество тепла, выделившееся к моменту полного разряда конденсатора с его теоретическим значением, равным .
- Сделайте выводы по графику и ответу и проведите расчёт погрешностей измерений.
Расстояние между пластинами
Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).
Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.
Разрядное устройство своими руками
Перед тем как измерить емкость, проверить кондёры на пробой или утечку, или если нужна замена несправного элемента необходимо его разрядить. Особенно актуально сделать правильный разряд у высоковольтных радиодеталей большой емкости. Накопленная энергия может сохраняться длительное время и неправильный демонтаж или хранение может нести угрозу для жизни.
Для безопасной разрядки высоковольтных конденсаторов можно собрать недорогое, простое в реализации электронное устройство. Оно разряжает вполне эффективно и безопасно.
Посмотрим на его принципиальную схему:
Напряжение с высоковольтного конденсатора поступает на гасящий резистор R1 и далее уходит на диодный ограничитель напряжения двустороннего типа.
Сам диодный ограничитель из двух параллельных цепочек диодов D1-D3 и D4-D6. Это сделано для того чтобы от любого диода в цепи снять напряжение порядка 2 вольт для работы светодиодных индикаторов D7, D8. Поступающий ток на светодиоды ограничивается резистором R2.
Светодиод запускает процесс разряда высоковольтного конденсатора до безопасного напряжения порядка двух вольт.
На процесс разряда может потребоваться некоторое время от 10 сек. и больше. Время разряда зависит от емкости подключенного кондёра и, какое остаточное напряжение в нем оставалось.
Как только светодиод потухнет можно провести окончательный разряд, с помощью отвертки закоротив выводы радиодетали.
Схема вполне работоспособна.
Всю плату можно собрать самостоятельно и поместить в пластиковый корпус.
Время, необходимое для зарядки конденсатора
В идеальных условиях, когда источник напряжения мощный, нет препятствий потоку электричества, конденсатор безупречен, время зарядки конденсатора будет равно 0.
На практике же на каждом участке цепи существует явное (резисторы) или неявное (провода, источник напряжения и т.п.) сопротивление. В этом случае время заряда конденсатора будет зависеть от сопротивления во всей цепи и его емкости.
В самом начале заряда на обкладках накопителя много свободного места, напряжение равно нулю. Начальный ток в этот момент максимален. По мере заполнения конденсатора заряженными частицами их поток постепенно снижается, U растет все медленнее. Когда не останется свободного места на обкладках, ток прекратится, напряжение станет максимальным и равным таковому источника.
Экспонента увеличения энергии в конденсаторе изображена на рисунке. Сама формула зависимости нарастания напряжения от времени заряда имеет следующий вид:
U=Uc*[1-e(-t/τ)]
где Uс – электродвижущая сила источника, t – время заряда, τ – постоянная времени, равная R*C (R – сопротивление).
За время τ зарядка конденсатора дойдет до (1 – 1/e)*100% ≈ 63% от U.
За 3τ – до (1 – 1/e3)*100% ≈ 95% от U.
За 5τ – до (1 – 1/e5)*100% ≈ 99% от U.
Время заряда конденсатора точно до уровня напряжения источника длится бесконечно долго.
Из вышеприведенной формулы вычисления напряжения можно вывести расчет времени зарядки накопителя до определенных показателей:
t = – ln (1 – U/Uc) * RC
Зарядка конденсатора от источника постоянной ЭДС
Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.
Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна ε
(Рис. 145). Полное электрическое соединение цепи (включающее и внутренне сопротивление источника) обозначим R . При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе (~U_C = frac{q}{C}) и резисторе (U_R = IR) равна ЭДС источника (varepsilon = U_C + U_R), что приводит к уравнению
(~IR = varepsilon — frac{q}{C}) . (1)
В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи (~I = frac{Delta q}{Delta t}), что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени
(~R frac{Delta q}{Delta t} = varepsilon — frac{q}{C}) . (2)
Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин
(~Delta varepsilon = Delta (IR) + Delta left (frac{q}{C} right )) .
Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t
и ( t + Δ t ), а затем из второго уравнения вычесть первое. Так как ЭДС источника постоянна, то ее изменение равно нулю Δ ε = 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Δ , поэтому полученное уравнение приобретает вид
(~R Delta I = — frac{1}{C} Delta q) .
Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда)
Будет интересно➡ Баласт для люминисцентных ламп
(~frac{Delta I}{Delta t} = -frac{1}{RC} I) . (3)
Математическая смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I
0 = I(0).
С уравнениями такого типа мы познакомились в «математическом отступлении», поэтому здесь его анализ проведем кратко.
В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна (~I_0 = Delta left (frac{Delta q}{Delta t} right )_0 = frac{varepsilon}{R}).
Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения (~overline{q} = Cvarepsilon) и ток в цепи прекратится.
Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае
(~tau = frac{overline{q}}{I_0} = RC) . (4)
Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату.
Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда.
Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса.
Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора
Рассмотрим теперь превращения различных форм энергии в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника.
На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q
, то сторонние силы совершили при этом работу A 0 = qε , при этом энергия конденсатора стала равной (~W = frac{q2}{2C} = frac{q varepsilon}{2}) , что в два раза меньше работы совершенной источником.
Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энергии источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки Δt
i ( i = 1,2,3…). Перепишем уравнение (1) в виде
(~varepsilon = IR + frac{q}{C}) , (5)
и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Δt
i, Δ q i = I iΔ t i . В результате получим
(~varepsilon Delta q_i = I_i R Delta q_i + frac{q_i}{C} Delta q_i) . (6)
Здесь обозначено q
i — заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл:[~varepsilon Delta q_i = delta A] — работа сторонних сил по перемещению порции заряда Δ q i;[~frac{q_i}{C} Delta q_i = Delta W_C] — увеличение энергии конденсатора при увеличении его заряда на Δ q i;[~I_i R Delta q_i = I2_i R Delta t_i = delta Q] — количество теплоты, выделившееся на резисторе, при протеканиипорции заряда Δ q i.
Таким образом, закон сохранения энергии, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки.
Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим:[~sum_i varepsilon Delta q_i = varepsilon overline{q} = A] — полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора;[~sum_i frac{q_i}{C} Delta q_i = frac{overline{q2}}{2C} = frac{varepsilon overline{q}}{2} = frac{C varepsilon2}{2}] — энергия заряженного конденсатора;
наконец, (~sum_i I_i R Delta q_i = sum_i I2_i R Delta t_i) — количество выделившейся на резисторе теплоты.
Принимая во внимание уравнение (3) и формулы из «математического отступления», последнюю сумму можно выразить в виде
(~Q = R sum_i I2_i Delta t_i = R frac{1}{2} I2_0 tau = R frac{1}{2} left ( frac{varepsilon}{R} right )2 RC = frac{C varepsilon2}{2}) . (6)
Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе (U_R = IR) от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии.
За малый промежуток времени через резистор протечет малый заряд Δq
i, при этом выделится количество теплоты (~delta Q_i = I_i R Delta q_i), которое численно равно площади узкой полоски, выделенной на рисунке.
Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости U
R( q ), то есть
ЭКСПЕРИМЕНТ 1
Определение ёмкости конденсатора методом разрядки
1.Соберите на рабочей части экрана замкнутую электрическую цепь, показанную ниже на рис.2. Для этого сначала щёлкните мышью на кнопке э.д.с.,расположенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора э.д.с., нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину э.д.с. и установите 10 В. Аналогичным образом включите в цепь 4 других источника тока. Суммарная величина э.д.с. батареи должна соответствовать значению, указанному в таблице 1 для вашего варианта.
Таким же образом разместите далее на рабочей части экрана 7 ламп Л1-Л7 ( кнопка ), Ключ К (кнопка ), вольтметр (кнопка ), амперметр (кнопка ), конденсатор (кнопка ). Все элементы электрической цепи соедините по схеме рис.1 с помощью монтажных проводов (кнопка ).
2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мыши замкните ключ К.
3. После установления в цепи стационарного тока ( должны погаснуть лампы Л5 и Л6 и светиться лампы Л1-Л4) запишите показания электроизмерительных приборов в таблицу 2.
4. Нажмите на кнопку «Стоп» и курсором мыши разомкните ключ К.
5. Двумя короткими щелчками мыши на кнопке «Старт» запустите и остановите процесс разрядки конденсатора. Показания амперметра будут соответствовать начальному току разрядки конденсатора I0. Запишите это значение в таблицу 3.
6. Вновь замкните ключ, зарядите конденсатор и повторите п.п. 5, 6 ещё 4 раза.
7. Для каждого опыта рассчитайте It= I0/2,7- силу тока, которая должна быть в цепи разрядки конденсатора через время релаксации t и запишите эти значения в таблицу 3.
8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундомер.
9. Внимательно наблюдайте за изменением показаний амперметра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, равном или близким к It. Запишите это значение времени t1 в таблицу 3.
10. Проделайте опыты п.п.8, 9 ещё 4 раза.
Таблица 1. Суммарное значение э.д.с. источников тока
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Э.д.с.,В | 50 | 49 | 48 | 47 | 46 | 45 | 44 | 43 |
Таблица 2. Определение сопротивления лампы.
| №п/п | I, А | U, В | R, Ом |
| Номер опыта | 1 | 2 | 3 | 4 | 5 | Среднее значение |
| I0, А | ||||||
| It, А | ||||||
| t, с | ||||||
| C, Ф |
Таблица 3. Результаты измерений и расчётов.
ОБРАБОТКА РЕЗУЛЬТАТОВ:
1. По закону Ома для участка цепи Л1-Л4: и результатам измерений, приведённым в таблице 2, определите сопротивление одной лампы.
2. По формуле (при разрядке конденсатора квазистационарный ток протекает по 6 последовательно соединённым лампам) определите ёмкость конденсатора и запишите эти значения в таблицу 3.
3. Рассчитайте погрешности измерений и сформулируйте выводы по результатам проделанной работы.
Последовательное соединение конденсаторов
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным. При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины, а остальные пластины заряжаются через влияние. При этом заряд пластины будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.
Типы соединений конденсаторов. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Будет интересно➡ Реактивное сопротивление
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы. Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке. Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения.
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора. Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд.
Стоит почитать: все об электолитических конденсаторах.
Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи. В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится. При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи. На каждый отдельный конденсатор в последовательной цепи падает разное напряжение. Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость конденсатора, тем большее напряжение на него упадет. Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов.
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3. Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной или последовательно-параллельной. Тем не менее, смешанное соединение может иметь как последовательный, так и параллельный характер.
Типы соединений конденсаторов.
Предназначение
Конденсатор для сабвуфера
Для начала узнаем, в чем предназначение этого элемента акустической системы. Нижем приводим подробную информацию:
- Отметим сразу, что он способен значительно улучшить параметры используемого усилителя, а значит является очень важной цепочкой во всей системе автозвука.
Примечание. Все сводится к тому, что современные низкочастотники или басовики моментами потребляют значительный ток и, тем самым, не в состоянии обеспечить их постоянное питание даже самая мощная АКБ.
- Почему же сабвуфер потребляет так много тока, может провода, проложенные к нему слишком толстые? Оказывается, дело вовсе не в этом. Какой бы толщины ни были провода и кабели, они, беспорно, обладают сопротивлением, вызывающим в определенный момент скачки тока и падение его мощи;
- Эксперты советуют не забывать и про работу дополнительных потребителей, что тоже не положительным образом действует на функционирование усилителя. Речь идет, к примеру, о кондиционере, работающим в жаркое время года и способным потреблять до 30 процентов энергии генератора. Все это ведет к тому, что при воспроизведении мощных басов, происходят нежелательные искажения звука, объяснимые неспособностью АКБ обеспечить нужный темп;
- В этих случаях, лучшим вариантом, который справляется на все 100%, является хороший, качественный конденсатор для басовика. Представляет собой этот элемент не что иное, как электролитик большой емкости.
Для сабвуфера конденсатор
Примечание. Подключение конденсатора должно происходить параллельно цепи питания усилителя.
- Правильный конденсатор для сабвуфера обладает малым внутренним сопротивлением. Это нужно для того, чтобы импульсный ток шел на усилитель моментально. Таким образом, полностью устраняются или до крайности минимизируются все возможные провалы.
Интересно. Примечательно, что конденсатор с той же чемпионской скоростью заряжается и как пионер, всегда готов вновь выдавать необходимую порцию для басовика.
Законы последовательного и параллельного соединения проводников
Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.
При последовательной схеме имеется одинаковая сила тока во всех проводниках:
I = I1 = I2.
Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:
U1 = IR1, U2 = IR2.
Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:
U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.
В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:
U1 = U2 = U.
А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:
I = I1 + I2.
Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение Принципиальная схема параллельного соединения Последовательное соединение Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.