Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток
— это вынужденные электромагнитные колебания, вызываемые в электрической цепи источником переменного (чаще всего синусоидального) напряжения.
Переменный ток присутствует всюду. Он течёт по проводам наших квартир, в промышленных электросетях, в высоковольтных линиях электропередач. И если вам нужен постоянный ток, чтобы зарядить аккумулятор телефона или ноутбука, вы используете специальный адаптер, выпрямляющий переменный ток из розетки.
Почему переменный ток распространён так широко? Оказывается, он прост в получении и идеально приспособлен для передачи электроэнергии на большие расстояния. Подробнее об этом мы поговорим в листке, посвящённом производству, передаче и потреблению электрической энергии.
А сейчас мы рассмотрим простейшие цепи переменного тока. Будем подключать к источнику переменного напряжения поочерёдно: резистор сопротивлением , конденсатор ёмкости и катушку индуктивности . Изучив поведение этих элементов, мы в следующем листке «Переменный ток. 2» подключим их одновременно и исследуем прохождение переменного тока через колебательный контур, обладающий сопротивлением.
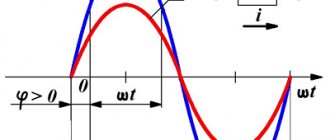
Напряжение на клеммах источника меняется по закону:
(1)
Как видим, напряжение может быть положительным и отрицательным. Каков смысл знака напряжения?
Всегда подразумевается, что выбрано положительное направление обхода контура. Напряжение считается положительным, если электрическое поле зарядов, образующих ток, имеет положительное направление. В противном случае напряжение считается отрицательным
.
Начальная фаза напряжения не играет никакой роли, поскольку мы рассматриваем процессы, установившиеся во времени. При желании вместо синуса в выражении (1) можно было бы взять косинус — принципиально от этого ничего не изменится.
Текущее значение напряжения в момент времени называется мгновенным значением напряжения
.
Переменный электрический ток
В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.
Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток
.
- Переменный электрический ток
— это ток, сила и направление которого периодически меняются.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω
по синусоидальному или косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,
где u
– мгновенное значение напряжения,
U
m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,
где φc – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Исходя из этого можно дать еще такое определение:
- Переменный ток
– это электрический ток, который изменяется с течением времени по гармоническому закону.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.
Происхождение индуктивного сопротивления
Вокруг проводника с движущимися заряженными существует магнитное поле. Оно слабое, но магнитная стрелка на него реагирует.
Если проводник намотать на катушку, то магнитное поле станет значительно более сильным. Оно приводит к появлению в катушке еще одного вида тока. Его возникновение в проводнике под действием магнитного поля называют электромагнитной индукцией. Обмотку называют катушкой индуктивности, а движение зарядов – индукционным током.
Одно из проявлений электромагнитной индукции – самоиндукция: возникновение дополнительной ЭДС в моменты резких изменений силы тока.
Это не колебания, возбуждаемые генератором, а изменения в момент включения, выключения, короткого замыкания. Для явления справедлива формула:
Esi = -L(ΔI/Δt).
Обозначения:
- Esi – ЭДС самоиндукции;
- ΔI – изменение силы тока;
- Δt – промежуток времени;
- L – индуктивность катушки, коэффициент самоиндукции.
Величина L – характеристика магнитных свойств катушки, измеряют ее в генри (Гн).
Индуктивность катушки равна 1 Гн, если при изменении в ней значения I на 1 А за 1 секунду возникает ЭДС самоиндукции 1 В.
Генератор переменного тока
Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.
- Генератором переменного тока
называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.
ЭДС индукции генератора изменяется по синусоидальному закону
\(e={\rm E}_{m} \cdot \sin \omega \cdot t,\)
где \({\rm E}_{m} =B\cdot S\cdot \omega\) — амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R
, через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке
\(i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\)
где \(I_{m} = \dfrac{B\cdot S\cdot \omega }{R}\) — амплитудное значение силы тока.
Основными частями генератора являются (рис. 1):
- индуктор
— электромагнит или постоянный магнит, который создает магнитное поле; - якорь
— обмотка, в которой индуцируется переменная ЭДС; - коллектор со щетками
— устройство, посредством которого снимается с вращающихся частей или подается по ним ток.
Рис. 1
Неподвижная часть генератора называется статором
, а подвижная —
ротором
. В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.
На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока. Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.
Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.
Из истории
. Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» — спросили его. Фарадей ответил: «Какая может быть польза от новорожденного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».
*Принцип действия
Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.
Пусть проводящая рамка площадью S
вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec{B}\) (см. рис. 1).
При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec{B}\) и нормали к плоскости рамки \(\vec{n}\) меняется со временем по линейному закону. Если в момент времени t
= 0 угол α0 = 0 (см. рис. 1), то
\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)
где ω — угловая скорость вращения рамки, ν — частота ее вращения.
В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом
\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)
Тогда согласно закону Фарадея индуцируется ЭДС индукции
\(e=-\Phi ‘(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.\)
Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.
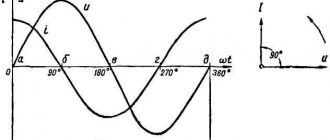
Действующие значения силы тока и напряжения
Пусть источник тока создает переменное гармоническое напряжение
\(u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)\)
Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R
, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)
где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины Um
,
Im
называются
амплитудными значениями напряжения и силы тока
. Зависящие от времени значения напряжения
u
и силы тока
i
называют
мгновенными
.
Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения
.
- Действующим (эффективным) значением силы
переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буквой I
.
- Действующим (эффективным) значением напряжения
переменного тока называется напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Обозначается буквой U
.
Действующие (I, U
) и амплитудные (
Im, Um
) значения связаны между собой следующими соотношениями:
\(I = \dfrac{I_{m} }{\sqrt{2}}, \; \; \; U =\dfrac{U_{m} }{\sqrt{2}}.\)
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
\(P = U\cdot I = I^{2} \cdot R = \dfrac{U^{2}}{R}.\)
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R
, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.
\(I=\dfrac{U}{R}.\;\;\;(3)\)
*Вывод формулы
Зная мгновенные значения u
и
i
, можно вычислить мгновенную мощность
\(p = u \cdot i,\)
которая, в отличие от цепей постоянного тока, изменяется с течением времени. С учетом уравнений (1) и (2) перепишем выражение для мгновенной мощности на резисторе в виде
\(p=U_{m} \cdot I_{m} \cdot \sin ^{2} \omega \cdot t=U_{m} \cdot I_{m} \cdot \dfrac{1-\cos 2\omega \cdot t}{2} =\dfrac{U_{m} \cdot I_{m} }{2} -\dfrac{U_{m} \cdot I_{m} }{2} \cdot \cos 2\omega \cdot t.\)
Первое слагаемое не зависит от времени. Второе слагаемое P
2 — функция косинуса удвоенного угла и ее среднее значение за период колебаний равно нулю (рис. 2, найдите сумму площади выделенных фигур с учетом знаков).
Рис. 2
Поэтому среднее значение мощности переменного электрического тока за период будет равно
\(\left\langle P \right\rangle =\dfrac{U_{m} \cdot I_{m} }{2}.\)
Тогда с учетом закона Ома \(\left(I_{m} =\dfrac{U_{m}}{R} \right)\) получаем:
\(\left\langle P \right\rangle = \dfrac{I_{m}^{2} }{2} \cdot R=\dfrac{U_{m}^{2} }{2R}. (4)\)
По определению действующих значений необходимо сравнивать мощности (количество теплоты в единицу времени) переменного и постоянного тока. Запишем уравнения для расчета мощности постоянного тока
\(P=I^{2} \cdot R=\dfrac{U^{2} }{R}\)
и сравним с уравнениями (4}:
\(\dfrac{I_{m}^{2}}{2} \cdot R = I^{2} \cdot R, \;\;\; I=\dfrac{I_{m}}{\sqrt{2}},\)
\(\dfrac{U_{m}^{2}}{2R} = \dfrac{U^{2}}{R}, \;\;\; U=\dfrac{U_{m}}{\sqrt{2}}.\)
Формулами
Параметры электрического тока всегда взаимосвязаны. Например, изменение величины нагрузки отображается на показателях других величин. Причем эти изменения подчиняются соответствующим законам, которые выражаются через формулы. Поэтому на практике для нахождения силы тока часто используют соответствующие формулы.
Через заряд и время
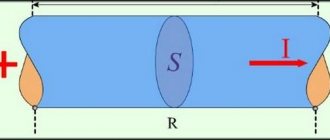
Вспомним определение (рис.1): электричество – это величина заряда, движимого силами электрического поля, преодолевающего за единицу времени условную плоскость проводника, называемую поперечным сечением проводника.
Рис. 1. Определение понятия сила тока
Таким образом, если известен электрический заряд, прошедший через проводник за определенное время, то не трудно найти величину этого заряда прошедшего за единицу времени, то есть: I = q/t
Через мощность и напряжение
В паспорте электроприбора обычно указывается его номинальная мощность и параметры электрической сети, для работы с которой он предназначен. Имея в распоряжении эти данные, можно вычислить силу тока по формуле: I = P/U.
Данное выражение вытекает из формулы для расчета мощности: P = IU.
Через напряжение или мощность и сопротивление
Силу электричества на участке цепи определяют по закону Ома. Для этого необходимо знать следующие параметры: сопротивление и напряжение на этом участке. Тогда I = U/R. Если известна мощность нагрузки, то ее можно выразить через квадрат силы тока умноженной на сопротивление участка: P = I2R, откуда
Для полной цепи эту величину вычисляют по закону Ома, но с учетом параметров источника питания.
Через ЭДС, внутреннее сопротивление и нагрузку R
Применяя закон Ома, адаптированный для полной цепи, вы можете вычислить максимальный ток по формуле I = ε / (R+r′), если известны параметры:
- внешнее сопротивление проводников (R);
- ЭДС источника питания (ε);
- внутреннее сопротивление источника, обладающего ЭДС (r′).
Примечание! Реальные источники питания обладают внутренним сопротивлением. Поскольку в электрической цепи показатель силы тока может уменьшаться в связи с возрастанием сопротивления источника питания или в результате падения ЭДС. Именно из-за роста внутреннего сопротивления садится аккумулятор и ослабевает ЭДС элементов питания.
Закон Джоуля-Ленца
Казалось бы, что расчет силы тока по количеству тепла, выделяющегося в результате нагревания проводника, не имеет практического применения. Однако это не так. Рассмотрим это на примере.
Пусть требуется найти силу тока во время работы электрочайника. Для этого доведите до кипения 1 кг воды и засеките время в секундах. Предположим, начальная температура составляла 10 ºС. Тогда Q = Cm(τ – τ0) = 4200 Дж/кг× 1 кг (100 – 10) = 378 000 Дж.
Рис. 2. Закон Джоуля-Ленца
Из закона Джоуля-Ленца (изображение на рис. 2) вытекает формула:
Измерив сопротивление электроприбора и подставив значения в формулу, получим величину потребляемого тока.