Лекция по электротехнике по теме «Цепи переменного тока с активным сопротивлением, индуктивностью и емкостью»

Цепь переменного тока с емкостью

Автор: Евгений Живоглядов. Дата публикации: 31 марта 2015. Категория: Статьи.

Если в цепь постоянного тока включить конденсатор (идеальный – без потерь), то в течение короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, соответствующего напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи или бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. Если включить конденсатор к переменному напряжению сети, то в течение первой четверти периода, когда напряжение сети будет возрастать (рисунок 1), конденсатор будет заряжаться.

Рисунок 1. Графики и векторная диаграмма для цепи переменного тока, содержащей емкость

По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимума, заряд конденсатора прекращается и ток в цепи становится равным нулю.

Ток в цепи конденсатора можно определить по формуле:

где q – количество электричества, протекающее по цепи.

Из электростатики известно:

q = C × uC = C × u ,

где C – емкость конденсатора; u – напряжение сети; uC – напряжение на обкладках конденсатора.

Окончательно для тока имеем:

Из последнего выражения видно, что, когда максимально (положения а, в, д), i также максимально. Когда

(положения б, г на рисунке 1), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное. В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд. Из рисунка 1 видно, что ток в цепи с емкостью в своих изменениях опережает по фазе на 90°

напряжение на обкладках конденсатора.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Поскольку мы отметили выше, что скорость изменения тока пропорциональна угловой частоте ω, из формулы

получаем аналогично, что скорость изменения напряжения также пропорциональна угловой частоте ω и для действующего значения тока имеем

I = 2 × π × f × C × U .

Обозначая

, где xC называется
емкостным сопротивлением, или реактивным сопротивлением емкости. Итак мы получили формулу емкостного сопротивления при включении емкости в цепи переменного тока. Отсюда, на основании выражения закона Ома, мы можем получить ток для цепи переменного тока, содержащей емкость:
Напряжение на обкладках конденсатора

UC = IC × xC .

Та часть напряжения сети, которая имеется на конденсаторе, называется емкостным падением напряжения, или реактивной слагающей напряжения, и обозначается UC.

Емкостное сопротивление xC, так же как индуктивное сопротивление xL, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.

Пример 1. Определить емкостное реактивное сопротивление конденсатора емкостью 5 мкФ при разных частотах сетевого напряжения. Расчет емкостного сопротивления произведем при частоте 50 и 40 Гц:

при частоте 50 Гц:

при частоте 400 Гц:

Применим формулу средней или активной мощности для рассматриваемой цепи:

P = U × I × cos φ .

Так как в цепи с емкостью ток опережает напряжение на 90°, то

φ = 90°; cos φ = 0 .

Поэтому активная мощность также равна нулю, то есть в такой цепи, как и в цепи с индуктивностью, расхода мощности нет.

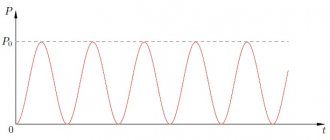
На рисунке 2 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

Рисунок 2. Кривая мгновенной мощности в цепи с емкостью

Энергию, запасаемую конденсатором к моменту прохождения напряжения на нем через максимум, можно определить по формуле:

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии повторяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без потерь.

Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.

§ 55. Емкость в цепи переменного тока

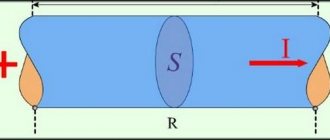
В главе I, § 10 был объяснен процесс заряда и разряда конденсатора, включенного в цепь постоянного тока. Рассмотрим теперь цепь переменного тока (рис. 58, а), в которую включена электрическая емкость (конденсатор). Активным сопротивлением этой цепи пренебрегаем (r

= 0).

Полярность зажимов генератора переменного тока, включенного в цепь с емкостью, меняется с частотой ω = 2πf

. В первую четверть периода (рис. 58, в) конденсатор заряжается и на его пластинах появляются противоположные по знаку электрические заряды (на левой пластине плюс, на правой — минус). При заряде конденсатора по проводам, соединяющим генератор с пластинами, перемещаются электрические заряды, следовательно, протекает зарядный ток, измеряемый миллиамперметром. Через диэлектрик конденсатора ток не проходит. Как видно на волновой диаграмме, в первую четверть периода во время заряда конденсатора напряжение на пластинах конденсатора возрастает от нуля до максимального значения, сила тока, наоборот, в начале заряда будет максимальной, а в конце заряда, когда напряжение на конденсаторе (
Uc
) окажется равным напряжению генератора (
Uг
), она станет равной нулю. За вторую четверть периода напряжение генератора постепенно убывает и становится равным нулю. В это время конденсатор разряжается. При этом разрядный ток, протекающий по проводам, имеет направление, противоположное направлению тока заряда. За третью четверть периода полярность на зажимах генератора изменится и напряжение возрастет от нуля до наибольшего значения. В это время конденсатор вновь зарядится, но полярность на его пластинах изменится. На левой пластине будет отрицательный заряд, на правой пластине — положительный заряд. По проводам пройдет зарядный ток, сила которого к концу заряда конденсатора, когда
Uc
=
Uг
, станет равной нулю. В четвертую часть периода напряжение генератора убывает и становится равным нулю. Конденсатор в это время вторично разряжается, и по проводам, соединяющим генератор с пластинами конденсатора, вновь протекает разрядный ток. Из сказанного следует, что за один период изменения переменного напряжения дважды происходит процесс заряда и разряда конденсатора и при этом в его цепи протекает переменный ток. Кроме того, при заряде и разряде конденсатора ток в цепи и напряжение не совпадают по фазе. Ток опережает по фазе напряжение на четверть периода, т. е. на 90°. Построим векторную диаграмму для цепи переменного тока с емкостью (рис. 58, б). Для этого отложим вектор тока
I
в выбранном масштабе по горизонтали. Чтобы на векторной диаграмме показать, что напряжение отстает от тока на угол φ = 90°, откладываем вектор напряжения
Uc
вниз под углом 90°. Выясним, от чего зависит сила тока в цепи с емкостью. Обозначим сопротивление цепи
Xc
и назовем его емкостным сопротивлением. Тогда закон Ома для цепи с емкостью можно выразить так:

где U

— напряжение генератора,
в
;
Xc
— емкостное сопротивление,
ом
;
I
— сила тока,
а
. Известно, что сила тока в цепи определяется количеством электрических зарядов, проходящих через поперечное сечение проводника в единицу времени:

Если в единицу времени по проводам протекает большое количество зарядов, то сила тока будет большой, и наоборот, когда по проводам в каждую секунду протекает малое количество зарядов, то сила тока оказывается незначительной. Допустим, что частота переменного тока, вырабатываемого генератором, большая. В этом случае в каждую секунду конденсатор много раз (часто) заряжается и разряжается. В проводах, идущих от генератора к пластинам конденсатора, будет перемещаться в каждую секунду большое количество электрических зарядов. Поэтому можно сказать, что в рассматриваемой цепи возникает большая сила тока и в данном случае, согласно закону Ома, емкостное сопротивление цепи Xc

оказывается малой величиной. Если же частота переменного тока генератора будет мала, то конденсатор в каждую секунду зарядится и разрядится меньшее количество раз. В связи с этим по проводам цепи в каждую секунду пройдет незначительное количество зарядов и сила тока будет мала, а следовательно, емкостное сопротивление цепи, наоборот, будет большим. Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально частоте переменного тока. Емкостное сопротивление зависит не только от частоты переменного тока, но и от величины емкости, включенной в цепь. Допустим, что в цепь включен конденсатор большой емкости. Количество электричества, которое накапливает конденсатор при заряде и отдает при разряде, прямо пропорционально его емкости:

q = C U

.

Чем больше емкость конденсатора, включенного в цепь переменного тока, тем большее количество электричества переместится при заряде и разряде по проводам, идущим от генератора к его пластинам. Поэтому в проводах возникает ток большой силы и в данном случае, согласно закону Ома, емкостное сопротивление цепи Xc

будет мало. Если же включенная в цепь емкость мала, то при заряде и разряде по проводам пройдет меньшее количество электрических зарядов и сила тока будет незначительной, следовательно, емкостное сопротивление цепи, наоборот, будет большим. Из сказанного можно сделать вывод, что емкостное сопротивление обратно пропорционально емкости. Таким образом, емкостное сопротивление:

где Xc

— емкостное сопротивление,
ом
; ω — угловая частота переменного тока,
рад/сек
;
С
— емкость,
ф
. Известно, что угловая частота ω = 2π
f
. Поэтому емкостное сопротивление можно определить так:

где f

— частота переменного тока,
гц
. Если включенная емкость измеряется в микрофарадах, то емкостное сопротивление

Если емкость измеряется в пикофарадах, то

Следует подчеркнуть, что имеется существенное различие между емкостным и активным сопротивлениями. Как известно, активная нагрузка безвозвратно потребляет энергию генератора переменного тока. Если же к источнику переменного тока присоединена емкость, то, как было рассмотрено выше, энергия генератора расходуется при заряде конденсатора на создание электрического поля между пластинами и возвращается обратно генератору при разряде конденсатора. Следовательно, емкостная нагрузка не потребляет энергию генератора, а в цепи с емкостью происходит «перекачивание» энергии из генератора в конденсатор и обратно. По этой причине емкостное сопротивление, как и индуктивное, называется реактивным.

Пример.

Конденсатор емкостью
С
= 2
мкф
включен в цепь переменного тока, частота которого 50
гц
. Определить: 1) его емкостное сопротивление при частоте
f
= 50
гц
; 2) емкостное сопротивление этого конденсатора переменному току, частота которого 500
гц
. Решение. Емкостное сопротивление конденсатора переменному току при частоте
f
= 50
гц
При частоте f

= 500
гц
Из приведенного примера видно, что емкостное сопротивление конденсатора уменьшается с повышением частоты, а с уменьшением частоты переменного тока емкостное сопротивление возрастает. Для постоянного тока, когда напряжение на зажимах цепи не изменяется, конденсатор практически обладает бесконечно большим сопротивлением и поэтому он постоянного тока не пропускает.
предыдущая страница

нально частоте и величине емкости (Рис.1.50).

Идеальная емкость

Конденсаторы являются идеальной емкостью в электрической цепи. В катушке индуктивности и конденсаторах активная мощность не потребляется, то есть $P=0$. В этот момент не происходит преобразования энергии в иные ее виды необратимого характера, а фиксируется лишь циркуляция имеющейся энергии. То есть электрическая энергия запасается в электрическом поле конденсатора или магнитном поле катушки. Процесс происходит примерно на протяжении 25 процентов времени периода. Затем энергия снова возвращается в сеть.

Определение 3

Конденсатор и катушку индуктивности из-за происходящих в них процессов иногда называют реактивными элементами. Их сопротивления принято называть реактивными. Исключение составляет резистор, так как он обладает активным сопротивлением.

Интенсивность обмена энергии характеризуется:

• самым большим значением скорости поступления энергии в магнитное поле катушки;
• наибольшей скоростью поступления энергии в электрическое поле конденсатора.

Эту интенсивность часто называют реактивной мощностью. Математическое выражение для реактивной мощности выглядит следующим образом:

$Q = UI sin \phi$

При индуктивной нагрузке $\phi \geq 0$ реактивная мощность будет иметь положительные значения. При опережающем токе емкостной нагрузке – отрицательные.

Реактивная мощность для идеальной катушки индуктивности будет пропорциональна максимальному запасу энергии в катушке и частоте.

Определение 4

Коэффициент мощности – отношение полной мощности к активной мощности. Он равен косинусу угла сдвига между напряжением и током.

Помимо активной и полной мощности используют понятие комплексной мощности. Реактивная мощность характеризуется циркуляцией между потребителем и источником. Реактивный ток не совершает работу, что приводит к неоправданным потерям в силовом оборудовании. Это ведет к повышению уровня установленной мощности. Поэтому в настоящее время существует тенденция на увеличение мощности в электрических цепях.

Многие потребители в виде различных электродвигателей и иных приборов и устройств используют нагрузку активно-индуктивного характера. При условии подключения к подобной нагрузке конденсаторов общий ток потребителя приблизится к значениям фазы по напряжению. Это означает, что он увеличивается, но общая величина тока уменьшается при условии постоянной активной мощности. Этот факт приводит к потере общей величины тока в электрических цепях. Конденсаторы призваны повышать мощность.

Мгновенная мощность

Для мгновенного определения мощности в электрической цепи вводится формула в виде:

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы

$p = ui$

Мгновенная мощность обладает двумя видами элементов:

• постоянной составляющей;
• гармонической составляющей.

Мгновенная мощность имеет угловую частоту, которая превышает угловую частоту напряжения и тока в два раза. При отрицательных значениях мгновенной мощности энергия будет возвращаться к источнику питания. Это говорит о том, что направления напряжения и тока имеют противоположные значения в двухполюснике.

Подобное возвращение энергии к источнику происходит из-за того, что идет энергетический запас в электрических и магнитных полях на уровне емкостных и индуктивных элементов. Они входят в состав двухполюсника.

Определение 2

Активная мощность – среднее значение мгновенной мощности за определенный период времени.

$P = UI cos \phi$

Активная мощность при потреблении пассивным двухполюсником не имеет отрицательных значений. На входе пассивного двухполюсника будет фиксироваться $cos \phi \geq 0$. Ситуация, при которой $P=0$, возможна в теории, но только для двухполюсника без активных сопротивлений. В нем должны быть:

Готовые работы на аналогичную тему

Курсовая работа Емкость и мощность электрической цепи 450 ₽ Реферат Емкость и мощность электрической цепи 220 ₽ Контрольная работа Емкость и мощность электрической цепи 210 ₽

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

• емкостные элементы;
• идеальные индуктивные элементы.

Рис.1.48

[/td]
где — амплитуда тока,

— начальная фаза.

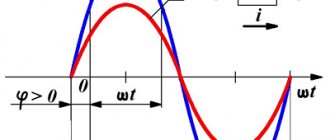
Сдвиг фаз между напряжением и током в цепи с емкостью равен т.е. ток в цепи с емкостью опережает по фазе приложенное напряжение на 90° (рис.1.49).

Комплексное сопротивление цепи с емкостью

ИНФОФИЗ

Рассмотрим по отдельности случаи подключения внешнего источника переменного тока к резистру с сопротивлением R

, конденсатору емкости
C
и катушки индуктивности
L
. Во всех трех случаях напряжения на резисторе, конденсаторе и катушке равны напряжению источника переменного тока.

1. Резистор в цепи переменного тока

Сопротивление R называют активным, потому что цепь с таким сопротивлением поглощает энергию.

Активное сопротивление — устройство, в котором энергия электрического тока необратимо преобразуется в другие виды энергии (внутреннюю, механическую)

Пусть напряжение в цепи меняется по закону: u = Umcos ωt ,

тогда сила тока меняется по закону: i = u/R = IRcosωt

u – мгновенное значение напряжения;

i – мгновенное значение силы тока;

IR

— амплитуда тока, протекающего через резистор.

Связь между амплитудами тока и напряжения на резисторе выражается соотношением RIR

=
UR
Колебания силы тока совпадают по фазе с колебаниями напряжения. (т.е. фазовый сдвиг между током и напряжением на резисторе равен нулю).

2. Конденсатор в цепи переменного тока

При включении конденсатора в цепь постоянного напряжения сила тока равна нулю, а при включении конденсатора в цепь переменного напряжения сила тока не равна нулю. Следовательно, конденсатор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.

Соотношение между амплитудами тока IC

и напряжения

UC

:

Ток опережает по фазе напряжение на угол π/2.

3. Катушка в цепи переменного тока

В катушке, включенной в цепь переменного напряжения, сила тока меньше силы тока в цепи постоянного напряжения для той же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи постоянного напряжения.

Соотношение между амплитудами тока IL

и напряжения
UL
:

ωLIL

=
UL
Ток отстает по фазе от напряжения на угол π/2.

Теперь можно построить векторную диаграмму для последовательного RLC-контура, в котором происходят вынужденные колебания на частоте ω. Поскольку ток, протекающий через последовательно соединенные участки цепи, один и тот же, векторную диаграмму удобно строить относительно вектора, изображающего колебания тока в цепи. Амплитуду тока обозначим через I

0. Фаза тока принимается равной нулю. Это вполне допустимо, так как физический интерес представляют не абсолютные значения фаз, а относительные фазовые сдвиги.

Векторная диаграмма на рисунке построена для случая, когда или В этом случае напряжение внешнего источника опережает по фазе ток, текущий в цепи, на некоторый угол φ.

Векторная диаграмма для последовательной RLC-цепи

Из рисунка видно, что

откуда следует

Из выражения для I

0 видно, что амплитуда тока принимает максимальное значение при условии

или

Явление возрастания амплитуды колебаний тока при совпадении частоты ω внешнего источника с собственной частотой ω0 электрической цепи называется электрическим резонансом

. При резонансе

Сдвиг фаз φ между приложенным напряжением и током в цепи при резонансе обращается в нуль. Резонанс в последовательной RLC-цепи называется резонансом напряжений

. Аналогичным образом с помощью векторной диаграммы можно исследовать явление резонанса при параллельном соединении элементов
R
,
L
и
C
(так называемый
резонанс токов
).

При последовательном резонансе (ω = ω0) амплитуды UC

и
UL
напряжений на конденсаторе и катушке резко возрастают:

Рисунок иллюстрирует явление резонанса в последовательном электрическом контуре. На рисунке графически изображена зависимость отношения амплитуды UC

напряжения на конденсаторе к амплитуде 0 напряжения источника от его частоты ω. Кривые на рисунке называются
резонансными кривыми
.