Всем доброго времени суток! В прошлой статье я рассказал о переменном напряжении и его параметрах. Данная статья, по сути, является продолжение предыдущей и затронет вопросы цепей переменного напряжения и тока, а также их воздействие на сопротивление, ёмкость и индуктивность в различных сочетаниях. Начнём с простейших цепей с синусоидальным переменным напряжением
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Сопротивление в цепи при переменном напряжении
Цепи переменного напряжения с сопротивлением является самыми простыми и наиболее часто встречающимися, поэтому начнём с них.
Переменное синусоидальное напряжение и ток в сопротивлении.
Допустим, что на сопротивление R подали переменное напряжение u, тогда, согласно с законом Ома, через данное сопротивление потечёт электрический ток i
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
ω – угловая частота,
t – время,
φ – начальная фаза
Таким образом, действующее I и среднее значение Icp переменного тока будут определяться следующими выражениями
Так как, напряжение и ток, в цепи с сопротивлением имеют одинаковую начальную фазу, то есть, происходит совпадение фаз и достижение амплитудных значений напряжения Um и тока Im происходит одновременно.
Выражение «совпадение фаз» связанно с понятием фазового сдвига ψ, которое определяет разность начальных фаз двух синусоид одинаковой частоты. Следовательно, фазовый сдвиг между напряжением и током при активном сопротивлении будет равен нулю
где φu – начальная фаза напряжения,
φi – начальная фаза тока.
Для оценки энергетических характеристик ввели понятие мощности, в цепях переменного напряжения существует несколько мощностных характеристик. Одной из них является мгновенная мощность Рm, определяемая, как произведение мгновенных значений напряжения и тока
где Um – амплитудное значение переменного напряжения,
Im – амплитудное значение переменного тока,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Таким образом, мгновенная мощность Рm изменяется с удвоенной частотой по сравнению с частотой напряжения и тока и колеблется в пределах от 0 до 2UI.
Еще одной энергетической характеристикой является среднее значение мощности за период Р или активная мощность, которая определяется следующим выражением
где Рm – мгновенная мощность,
U – действующее значение переменного напряжения,
I – действующее значение переменного тока.
Переменный ток. Его характеристики
Электрическим током называют направленное движение заряженных частиц. Количественными характеристиками тока являются его сила тока (отношение заряда переносимого через поперечное сечение проводника в единицу времени) и его плотность, определяемая соотношением. Единицей измерения силы тока является ампер (1А — характерное значение тока, потребляемого бытовыми электронагревательными приборами). Необходимыми условиями существования тока являются наличие свободных носителей зарядов, замкнутой цепи и источника ЭДС (батареи), поддерживающего направленное движение.
Электрический ток может существовать в различных средах: в металлах, вакууме, газах, в растворах и расплавах электролитов, в плазме, в полупроводниках, в тканях живых организмов. При протекании тока практически всегда происходит взаимодействие носителей зарядов с окружающей средой, сопровождающееся передачей энергии последней в виде тепла. Роль источника ЭДС как раз и состоит в компенсации тепловых потерь в цепях. Электрический ток в металлах обусловлен движением относительно свободных электронов через кристаллическую решетку. Причины существования свободных электронов в проводящих кристаллах может быть объяснена только на языке квантовой механики.
Опыт показывает, что сила электрического тока, протекающего по проводнику, пропорциональна приложенной к его концам разности потенциалов (закон Ома). Постоянный для выбранного проводника коэффициент пропорциональности между током и напряжением называют электрическим сопротивлением. Сопротивление измеряют в омах (сопротивление человеческого тела составляет около 1000 Ом). Величина электрического сопротивления проводников слабо возрастает при увеличении их температуры. Это связано с тем, что при нагревании узлы кристаллической решетки усиливают хаотические тепловые колебания, что препятствует направленному движению электронов.
Во многих задачах непосредственный учет колебаний решетки оказывается весьма трудоемким. Для упрощения взаимодействия электронов с колеблющимися узлами оказывается удобным заменить их столкновениями с частицами газа гипотетических частиц — фононов, свойства которых подбираются так, чтобы получить максимально приближенное к реальности описание и могут оказываться весьма экзотическими. Объекты такого типа весьма популярны в физике и называются квазичастицами. Помимо взаимодействий с колебаниями кристаллической решетки движению электронов в кристалле могут препятствовать дислокации — нарушения регулярности решетки. Взаимодействия с дислокациями играют определяющую роль при низких температурах, когда тепловые колебания практически отсутствуют.
Некоторые материалы при низких температурах полностью утрачивают электрическое сопротивление, переходя в сверх проводящее состояние. Ток в таких средах может существовать без каких-либо ЭДС, поскольку потери энергии при столкновениях электронов с фононами и дислокациями отсутствуют. Создание материалов, сохраняющих сверхповодящее состояние при относительно высоких (комнатных) температурах и небольших токах является весьма важной задачей, решение которой произвело бы настоящий переворот в современной энергетике, т.к. позволило бы передавать электроэнергию на большие расстояния без тепловых потерь.
В настоящее время электрический ток в металлах используется главным образом для превращения электрической энергии в тепловую (нагреватели, источники света) или в механическую (электродвигатели). В последнем случае электрический ток используется в качестве источника магнитных полей, взаимодействие с которыми других токов вызывает появление сил.
Переменный ток
Как известно, сила тока в любой момент времени пропорциональна ЭДС источника тока (закон Ома для полной цепи). Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток.
Однако в современной технике широко применяются не только источники постоянного тока, но и различные генераторы электрического тока, в которых ЭДС периодически изменяется. При подключении в электрическую цепь генератора переменной ЭДС в цепи возникают вынужденные электромагнитные колебания или переменный ток.
Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника.
Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой щ по синусоидальному или косинусоидальному закону:
где u – мгновенное значение напряжения, Um – амплитуда напряжения, щ – циклическая частота колебаний. Если напряжение меняется с частотой щ, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения.
Поэтому в общем случае:
где – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.
Резистор в цепи переменного тока
Пусть цепь состоит из проводников с малой индуктивностью и большим сопротивлением R (из резисторов). Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление R называется активным потому, что, только на нем выделяется энергия, т.е.
Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением.
Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 1).
Пусть напряжение на концах цепи меняется по гармоническому закону:
Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома:
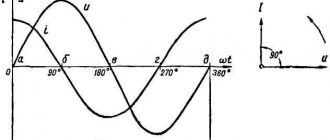
Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 2), а амплитуда силы тока равна амплитуде напряжения, деленной на сопротивление:
При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты и практически совпадает с его электрическим сопротивлением в цепи постоянного тока.
1.1 Катушка в цепи переменного тока
Индуктивность влияет на силу переменного тока в цепи. Это можно обнаружить с помощью простого опыта. Составим цепь из катушки большой индуктивности и лампы накаливания (рис. 3). С помощью переключателя можно присоединять эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть одинаковы. Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы тока в рассматриваемой цепи меньше силы постоянного тока.
Объясняется это самоиндукцией. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь по прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех установившихся значений, которые она приобрела бы с течением времени при постоянном напряжении, равном максимальному значению переменного напряжения. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью L цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.
Докажем это математически. Пусть в цепь переменного тока включена идеальная катушка с электрическим сопротивлением провода, равным нулю (рис. 4).
При изменениях силы тока по гармоническому закону:
в катушке возникает ЭДС самоиндукции:
где L – индуктивность катушки, щ – циклическая частота переменного тока.
Так как электрическое сопротивление катушки равно нулю, то ЭДС самоиндукции в ней в любой момент времени равна по модулю и противоположна по знаку напряжению на концах катушки, созданному внешним генератором:
Следовательно, колебания напряжения на катушке индуктивности опережают колебания силы тока на р/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на р/2.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (рис. 5). В момент, когда напряжение становится равным нулю, сила тока максимальна по модулю.
Произведение Im ⋅ L ⋅ щ является амплитудой колебаний напряжения на катушке:
Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний силы тока в ней называется индуктивным сопротивлением (обозначается XL):
Связь амплитуды колебаний напряжения на концах катушки с амплитудой колебаний силы тока в ней совпадает по форме с выражением закона Ома для участка цепи постоянного тока:
В отличие от электрического сопротивления проводника в цепи постоянного тока, индуктивное сопротивление не является постоянной величиной, характеризующей данную катушку. Оно прямо пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в катушке при постоянном значении амплитуды колебаний напряжения должна убывать обратно пропорционально частоте. Постоянный ток вообще «не замечает» индуктивности катушки. При щ = 0 индуктивное сопротивление равно нулю (XL = 0).
Зависимость амплитуды колебаний силы тока в катушке от частоты приложенного напряжения можно наблюдать в опыте с генератором переменного напряжения, частоту которого можно изменять. Опыт показывает, что увеличение в два раза частоты переменного напряжения приводит к уменьшению в два раза амплитуды колебаний силы тока через катушку.
1.2 Конденсатор в цепи переменного тока
Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы.
При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения.
Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.
Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока.
При изменениях напряжения на обкладках конденсатора по гармоническому закону:
заряд на его обкладках изменяется по закону:
Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. Поэтому колебания силы тока в цепи происходят по закону:
Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на р/2 или колебания силы тока опережают по фазе колебания напряжения на р/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д.
Произведение Um ⋅ щ ⋅ C является амплитудой колебаний силы тока:
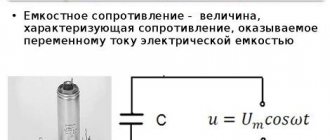
Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается ХC):
Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора:
Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.
1.3 Закон Ома для электрической цепи переменного тока
Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки (рис. 8). Если к выводам этой электрической цепи приложить электрическое напряжение, изменяющееся по гармоническому закону с частотой щ и амплитудой Um, то в цепи возникнут вынужденные колебания силы тока с той же частотой и некоторой амплитудой Im. Установим связь между амплитудами колебаний силы тока и напряжения
В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения:
Во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со скоростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону:
Колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, колебания напряжения на конденсаторе отстают по фазе на р/2 от колебаний силы тока, а колебания напряжения на катушке опережают по фазе колебания силы тока на р/2.
Поэтому уравнение (1) можно записать так:
где URm, UCm и ULm – амплитуды колебаний напряжения на резисторе, конденсаторе и катушке.
Амплитуду колебаний напряжения в цепи переменного тока можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм.
При построении векторной диаграммы необходимо учитывать, что колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, поэтому вектор, изображающий амплитуду напряжения URm, совпадает по направлению с вектором, изображающим амплитуду силы тока Im Колебания напряжения на конденсаторе отстают по фазе на р/2 от колебаний силы тока, поэтому вектор
UCm отстает от вектора Im на угол 90°. Колебания напряжения на катушке опережают колебания силы тока по фазе на р/2, поэтому вектор ULm опережает вектор Im на угол 90° (рис. 9).
На векторной диаграмме мгновенные значения напряжения на резисторе, конденсаторе и катушке определяются проекциями на горизонтальную ось векторов Rm, Cm, Lm вращающихся с одинаковой угловой скоростью щ против часовой стрелки. Мгновенное значение напряжения во всей цепи равно сумме мгновенных напряжений uR, uC, и uL на отдельных элементах цепи, т.е. сумме проекций векторов URm, UCm и ULm на горизонтальную ось. Так как сумма проекций векторов на произвольную ось равна проекции суммы этих векторов на ту же ось, то амплитуду полного напряжения можно найти как модуль суммы векторов:
Из рисунка 9 видно, что амплитуда напряжений на всей цепи равна:
Или
Отсюда
Введя обозначение для полного сопротивления цепи переменного тока:
выразим связь между амплитудными значениями силы тока и напряжения в цепи переменного тока следующим образом:
Это выражение называют законом Ома для цепи переменного тока.
Из векторной диаграммы, приведенной на рисунке 9, видно, что фаза колебаний полного напряжения равна щt + ц. Поэтому мгновенное значение полного напряжения определяется формулой:
Начальную фазу ц можно найти из векторной диаграммы:
Величина cos ц играет важную роль при вычислении мощности в электрической цепи переменного тока.
1.4 Мощность в цепи переменного тока
Мощность в цепи постоянного тока определяется произведением напряжения на силу тока:
Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение U?I характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным.
Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой:
Пусть напряжение на концах цепи меняется по гармоническому закону:
При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период.
Чтобы найти среднюю мощность за период, преобразуем полученную формулу таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов:
Выражение для мгновенное мощности состоит из двух слагаемых. Первое не зависит от времени, а второе дважды за каждый период изменения напряжения изменяет знак: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течении другой части возвращается обратно. Поэтому среднее значение второго слагаемого за период равно нулю.
Следовательно, средняя мощность Р за период равна первому члену, не зависящему от времени:
При совпадении фазы колебаний силы тока и напряжения (для активного сопротивления R) среднее значение мощности равно:
Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = IU = I2R), вводятся понятия действующих значений силы тока и напряжения. Из равенства мощностей получим:
Действующим значением силы тока называют величину, в √2 раз меньшую ее амплитудного значения:
Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока.
Аналогично можно доказать, что действующее значение переменного напряжения в √2 раз меньше его амплитудного значения:
Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение (10) можно переписать:
Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз цc между напряжением и током. Множитель cos цc в формуле называется коэффициентом мощности.
В случае, когда цc = ± р/2, энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при цc = – р/2 (чисто индуктивное сопротивление участка цепи).
График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть.
Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит.
При проектировании цепей переменного тока нужно добиваться, чтобы cos цc не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов.
Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos цc в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой.
Это уменьшает коэффициент мощности всей цепи. Повышение cos цc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos цc < 0,85.
Теория
С одной стороны каждому известно, что первое знакомство человечества с электрической энергией произошло на примере постоянного тока. Только в 1831 году исследование явления магнитной индукции привели к генерации переменных токов. Первые эксперименты задействовали электрический проводник, помещаемый в магнитный поток.
Для примера вам следует рассмотреть обычный проводник, приведенный в состояние замкнутого контура, края проводника можно подключить к измерительному прибору для фиксации изменения электрических величин.
Далее вам необходимо:
- взять хороший магнит, если под рукой имеется мощный неодимовый, то он подойдет лучше всего;
- подключите проводник к гальванометру, всю электрическую цепь положите на стол или другую поверхность из изолирующего материала;
- поднесите магнит к проводнику как можно ближе, желательно, чтобы расстояние было не больше 10 мм;
- сделайте резкое движение в перпендикулярной плоскости по отношению к проводнику;
- обратите внимание на прибор, стрелка гальванометра отклонится от равновесного положения в какую-либо сторону – в результате электромагнитных колебаний в проводнике наводится ЭДС индукции, которая и обуславливает возникновение переменного тока в замкнутом контуре.
Повторите манипуляцию с магнитом несколько раз, и вы увидите, как гальванометр равномерно отклоняется в сторону, по мере приближения полюса к проводнику и так же равномерно возвращается в исходную позицию по мере удаления магнита. Отклонение стрелки свидетельствует об изменении величины тока и потенциала, индуцируемых в металле. Амплитуда колебаний тока не постоянна во времени, из-за чего данная величина и называется переменной.
Заметьте, если перемещать возле провода один магнитный полюс, то стрелка будет отклоняться в одном направлении, если повернуть противоположным магнитным полюсом, то и направление отклонения стрелки соответственно изменится.
Один контур представляет собой лишь пример для понимания сути получения переменного электрического тока, так как ЭДС в нем будет слишком малой и мощности не хватит даже для питания светодиода. В промышленных масштабах вместо вращения витка используют целые обмотки с множеством витков. На практике не имеет значения, происходит движение магнита относительно проводника или это замкнутый контур движется по отношению к полюсу магнита.
Поэтому для изменения ЭДС в обмотках генератора может применяться как принцип вращения ротора из магнитного материала внутри обмоток статора, так и наоборот, обмоток ротора внутри магнитного статора.
Сама величина электродвижущей силы определяется из соотношения физических параметров по такой формуле:
где n – это количество витков обмоток
а соотношение dФB/dt – это скорость изменения электромагнитной индукции во времени.
Формула закона Ома
Первый Закон Ома устанавливает, что разница потенциалов между двумя точками резистора пропорциональна току. Более того, согласно этому закону, соотношение между потенциалом и током всегда является постоянным для омических резисторов.
V = RI, где:
V — напряжение/электропотенциал (В);
R — электросопротивление (ом);
I — электрический ток.
Формула
В нем U является скалярной величиной и меряется в (В). Разница в электропотенциалах между двумя точками цепи, указывает на наличие электросопротивления. Когда I проходит через резистивный элемент R, происходит падение электрического потенциала. Это различие возникает из-за рассеивания энергии, называемым эффектом Джоуля. I измеряет поток зарядов через тело в (А) и прямо пропорционален сопротивлению провода.
Второй закон Ома говорит о том, что электросопротивление R представляет собой свойство из тела, которое регулирует проходимость I. Это свойство зависит от геометрических факторов тела, таких как длина или площадь сечения участка и от вызываемой величины R. Его количество зависит исключительно от материала участка.
R= ρ*L/S, где:
R — электросопротивление (Ом);
ρ — удельное электросопротивление провода (Ом.м);
L — протяженность проводника (м);
S — площадь сечения провода (м²).
Омическим резистором называется любое тело, способное представлять постоянное сопротивление для данного диапазона напряжений. График напряжения как функция тока для омических резисторов является линейным. Резистор можно считать омическим в диапазоне, в котором его потенциал линейно возрастает с ростом I.
Сопротивление можно понимать как наклон линии, заданный тангенсом угла. Как известно, тангенс определяется, как отношение между противоположным и соседним сторонами, и, в случае, когда сопротивления омические, может быть рассчитан по формуле: R = U / I.
Треугольник
Чтобы помочь запомнить формулу, можно использовать треугольник с одной горизонтальной стороной и вершиной вверху, как пирамиду. Это иногда называют законом треугольника Ома. В верхнем его углу находится буква V, в левом углу — буква I, а в правом нижнем углу — R.
Обратите внимание! Чтобы использовать треугольник, прикрыть неизвестный параметр, а затем, рассчитать его из двух других. Если они находятся на одной линии, они умножаются, но если одна находится над другой, их следует разделить. Другими словами, если необходимо рассчитать I, напряжение делится на сопротивление, то есть V / R.
Какой ток в розетке – постоянный или переменный
Люди, мало-мальски знакомые с электротехникой, без труда ответят на вопрос о том, какой ток в розетке. Конечно же переменный. Этот вид электричества гораздо проще производить и передавать на большие расстояния, а потому выбор в пользу переменного тока очевиден.
Существует два вида тока — постоянный и переменный. Чтобы понять разницу и определить, постоянный или переменный ток находится розетке, следует вникнуть в некоторые технические особенности. Переменный ток имеет свойство изменяться по направлению и величине. Постоянный же ток обладает устойчивыми качествами и направлением передвижения заряженных частиц.
Переменный ток выходит из генераторов электростанции с напряжением, составляющим 220–440 тысяч вольт. При подходе к многоквартирному зданию ток уменьшается до 12 тысяч вольт, а на трансформаторной станции преобразуется в 380 вольт.
Совет
Напряжение между фазами именуют линейным. Низковольтный участок понижающей подстанции выдает три фазы и нулевой (нейтральный) провод. Подключение энергопотребителей осуществляется от одной из фаз и нулевого провода.
Таким образом, в здание заходит переменный однофазный ток с напряжением 220 вольт.
Схема распределения электроэнергии между домами представлена ниже:
В жилище электричество поступает на счетчик, а далее — через автоматы на коробки каждого помещения. В коробках имеется разводка по комнате на пару цепей — розеточную и осветительной техники.
Автоматы могут предусматриваться по одному для каждого помещения или по одному для каждой цепи.
С учетом того, на сколько ампер рассчитана розетка, она может быть включена в группу или быть подключенной к выделенному автомату.
Переменный ток составляется примерно 90% всей потребляемой электроэнергии. Столь высокий удельный вес вызван особенностями этого вида тока — его можно транспортировать на значительные расстояния, изменяя на подстанциях напряжение до нужных параметров.
Источниками постоянного тока чаще всего являются аккумуляторные батареи, гальванические элементы, солнечные панели, термопары.
Постоянный ток широко используется в локальных сетях автомобильного и воздушного транспорта, в компьютерных электросхемах, автоматических системах, радио- и телевизионной аппаратуре.
Постоянный ток применяется в контактных сетях железнодорожного транспорта, а также на корабельных установках.
На схеме, представленной ниже, показаны принципиальные отличия между постоянным и переменным токами.
Параметры домашней электрической сети
Основными параметрами электричества являются его напряжение и частота. Стандартное напряжение для домашних электросетей — 220 вольт. Общепринятая частота — 50 герц. Однако в США используется другое значение частоты — 60 герц. Параметр частоты задается генерирующим оборудованием и является неизменным.
Будет интересно➡ Провод и кабель ПВС. Описание, расшифровка и техническое применение провода типа ПВС
Напряжение в сети конкретного дома или квартиры может быть отличным от номинала (220 вольт). На данный показатель влияет техническое состояние оборудования, сетевые нагрузки, загруженность подстанции. В результате напряжение может отклоняться от заданного параметра в ту или другую сторону на 20–25 вольт.
Токовая нагрузка
Все розетки имеют определенную маркировку, по которой можно судить о допустимой токовой нагрузке. Например, обозначение «5A» указывает на максимальную силу тока в 5 ампер. Допустимые показатели следует соблюдать, поскольку в противном случае возможен выход оборудования из строя, в том числе его возгорание.
Маркировка на розетках показана на рисунке внизу:
Ко всем легально продаваемым электроприборам прилагается паспорт, где указана потребляемая мощность или номинал токовой нагрузки.
Крупнейшими потребителями электроэнергии являются такие электробытовые приборы, как кондиционеры, микроволновые печи, стиральные машины, кухонные электроплиты и духовки.
Таким приборам для нормальной работы понадобится розетка с нагрузкой не меньше 16 ампер.
Обратите внимание
Если же в документации к электробытовой технике отсутствуют сведения о потребляемых амперах (сила тока в розетке), определение нужных величин осуществляется по формуле электрической мощности:
Показатель мощности имеется в паспорте, напряжение сети известно. Чтобы определить потребление электричества, нужно показатель мощности (указывается только в ваттах) разделить на величину напряжения.
Где и когда можно применять закон Ома
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
В чем заключается принцип работы переменного тока
Английская аббревиатура АС (Alternating Current) обозначает ток, меняющий на временных отрезках свое направление и величину. Отрезок синусоиды «~» – его условная маркировка на приборах. Применяется также нанесение после этого значка и других характеристик.
Ниже приведен рисунок с главными характеристиками данного вида тока – номинальными показателями частоты и действующего напряжения.
Следует отметить особенности изменения на левом графике, выполненном для однофазного тока, величины и направления напряжения с осуществлением перехода на ноль за определенный промежуток времени Т. На одну треть периода выполняется смещение трех синусоид при трехфазном токе на другом графике.
О и «б» обозначены фазы. Любой из нас имеет представление о наличии в обычной розетке 220В. Но для многих будет открытием, что максимальное или именуемое по-другому амплитудным значение больше действующего на величину равную корню из двух и составляет 311 Вольт.
Очевидно, что в случае с током постоянного вида параметры направления и напряжения остаются неизменными, а вот для переменного наблюдается трансформация данных величин. На рисунке обратное направление – это область графика ниже нуля.
Переходим к частоте. Под этим понятием подразумевают отношение периодов (полных циклов) к условной единице временного отрезка меняющегося тока. Данный показатель измеряется в Герцах. Стандартная европейская частота – 50, в США применяемый норматив – 60Г.
Эта ве6личина показывает количество изменений направления тока за одну секунду на противоположное и возвращение в исходное состояние.
Переменный ток присутствует при прямом подключении приборов потребления к электрощитам и в розетках. По какой причине здесь отсутствует постоянный ток? Это сделано для того, чтобы получить возможность без особых потерь получать нужное напряжение в любом количестве способом применения трансформаторов. Эта методика остается лучшим способом передавать электроэнергию в промышленных масштабах на значительные расстояния с минимальными потерями.
Номинальное напряжение, которое подается мощными генераторами электростанций, на выходе составляет порядка 330 000-220 000 Вольт. На подстанции, расположенной в зоне потребления, происходит трансформация данной величины до показателей 10 000В с переходом в трехфазный вариант 380 Вольт. Выполняется подача в отдельный дом и на вашу квартиру попадает напряжение однофазного типа. Напряжение между нулем и фазой составит 220 В, а в щите между разными фазами подобный показатель равняется 380 Вольт.
Формула напряжения
В физике есть формула, хотя практического применения она не имеет. Официальная формула записывается так.
формула напряжения
где
A — это работа электрического поля по перемещению заряда по участку цепи, Джоули
q — заряд, Кулон
U — напряжение на участке электрической цепи, Вольты
На практике напряжение на участке цепи выводится через закон Ома.
Будет интересно➡ Реле контроля напряжения
напряжение из закона Ома
где
I — сила тока, Амперы
R — сопротивление, Омы
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Сила тока
Электрическим током называется упорядоченное (направленное) движение заряженных частиц. Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:
$I={∆q}/{∆t}$
Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время. Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_{0}nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t={∆l}/{υ}$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:
$I={∆q}/{∆t}={q_{0}nS∆l·υ}/{∆l}=q_{0}nυS$
В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836). Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока. Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.