Расчет величины индукции магнитных полей по формуле и определение индуктивности

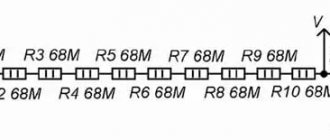
На рисунке выше показана однослойная катушка индуктивности: D

c — диаметр катушки,
D
— диаметр оправки или каркаса катушки,
p
— шаг намотки катушки,
d
— диаметр провода без изоляции и
d
i — диаметр провода с изоляцией

Для расчета индуктивности LS применяется приведенная ниже формула из статьи Р. Уивера (R. Weaver) Численные методы расчета индуктивности:

Здесь

— диаметр оправки или каркаса катушки в см,

— длина катушки в см,

— число витков и

— индуктивность в мкГн.

Эта формула справедлива только для соленоида, намотанного плоским проводом. Это означает, что катушка намотана очень тонкой лентой без зазора между соседними витками. Она является хорошим приближением для катушек с большим количеством витков, намотанных проводом круглого сечения с минимальным зазором между витками. Американский физик Эдвард Беннетт Роса (Edward Bennett Rosa, 1873–1921) работавший в Национального бюро стандартов США (NBS, сейчас называется Национальное бюро стандартов и технологий (NIST) разработал так называемые корректирующие коэффициенты для приведенной выше формулы в форме (см. формула 10.1 в статье Дэвида Найта, David W. Knight):

Здесь L

S — индуктивность плоской спирали, описанная выше, и

где k

s — безразмерный корректирующий коэффициент, учитывающий разницу между самоиндукцией витка из круглого провода и витка из плоской ленты;
k
m — безразмерный корректирующий коэффициент, учитывающий разницу в полной взаимоиндукции витков из круглого провода по сравнению с витками из плоской ленты;
D
c — диаметр катушки в см, измеренный между центрами проводов и
N
— число витков.

Величина коэффициента Роса k

m определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта:

Коэффициент Роса k

s, учитывающий различие в самоиндукции, определяется по формуле 10.4 в статье Д. Найта:

Здесь p

— шаг намотки (расстояние между витками, измеренное по центрам проводов) и
d
— диаметр провода. Отметим, что отношение
p/d
всегда больше единицы, так как толщина изоляции провода конечна, а минимально возможное расстояние между двумя соседними витками с очень тонкой изоляцией, расположенными без зазора, равна диаметру провода
d
.

Способы расчёта

Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.

Через силу тока

Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:

L — индуктивность контура (в генри);
Ф — величина магнитного потока, измеряемого в веберах;
I — сила тока в катушке (в амперах).

Соленоид конечной длины

Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:

µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр);
N — количество витков в катушке;
S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
l — длина соленоида в метрах.

Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:

W — энергия магнитного потока, измеряемая в джоулях;
I — сила тока в амперах.

Катушка с тороидальным сердечником

В большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:

N — число витков катушки;
µ — относительная магнитная проницаемость;
µ0 — магнитная постоянная;
S — площадь сечения сердечника;
π — математическая постоянная, равная 3,14;
r — средний радиус тора.

Длинный проводник

Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:

l — длина проводника в метрах;
r — радиус сечения провода, измеряемый в метрах;
µ0 — магнитная постоянная;
µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
π — число Пи;
ln — обозначение логарифма.

Индуктивность контура — теоретические основы

Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.

Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:

Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.

По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током катушки L=Ψ/i.

Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.

Поток сцепления катушки индуктивности равен Ψ=L×i.

В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.

Напряжение на индуктивности уравновешивает ЭДС и может быть записано в виде uL=-eL=dΨ/dt=L×di/dt.

Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.

Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.

Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.

Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.

Одновитковой контур и катушка

Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:

L=Ф/I.

Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.

Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:

L=L1∙N2.

Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.

Как найти индуктивность контура

Формула, которая является простейшей для нахождения величины, следующая:

L = F : I,

где F – магнитный поток, I – ток в контуре.

Через индуктивность можно выразить ЭДС самоиндукции:

Ei = -L х dI : dt.

Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.

Переменная индуктивность дает возможность найти и энергию магнитного поля:

W = L I2 : 2.

Что такое индуктивность

Этим термином обозначают зависимость, которая устанавливается между силой тока в проводнике (I) и созданным магнитным потоком (Ф):

L = Ф/ I.

С учетом базового определения несложно понять зависимость индуктивности от свойств окружающей среды, оказывающей влияние на распределение силовых линий. Определенное значение имеют размеры и конфигурация проводящего элемента.

Индуктивность подобна механической инерции. Только в данном случае речь идет о действиях с электрическими величинами. Этим коэффициентом характеризуют способность рассматриваемого компонента противодействовать изменению проходящего через него тока.

Корпус приставки к мультиметру

Тело можно сделать из готовой коробки подходящего размера, а можно сделать коробку своими руками. Вы можете выбрать любой материал, например, пластик или тонкий стеклопластик. Коробка адаптирована к размерам стола и имеет отверстия для крепления. Также есть отверстия для подключения проводки. Все фиксируется винтиками.

Приставка питается от сети через блок питания 12 В.

ЭДС индукции

Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.

Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.

Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.

Введение

Если бы кому-нибудь пришла в голову идея провести опрос населения Земли на тему «Что вы знаете об индуктивности?», то подавляющее число опрашиваемых просто пожало бы плечами. А ведь это второй по многочисленности вслед за транзисторами технический элемент, на котором зиждется современная цивилизация! Любители детективов, припомнив, что в своей юности зачитывались захватывающими рассказами сэра Артура Конан Дойла о приключениях знаменитого сыщика Шерлока Холмса, с разной степенью уверенности пробормочут что-то о методе, которым вышеозначенный сыщик пользовался. При этом подразумевая метод дедукции, который, наравне с методом индукции, является основным методом познания в западной философии Нового времени.

При методе индукции происходит исследование отдельных фактов, принципов и формирование общих теоретических концепций на основе полученных результатов (от частного к общему). Метод дедукции, наоборот, предполагает исследование от общих принципов, законов, когда положения теории распределяются на отдельные явления.

Следует отметить, что индукция, в смысле метода, не имеет сколько-нибудь прямого отношения к индуктивности, просто они имеют общий латинский корень inductio

— наведение, побуждение — и обозначают совершенно разные понятия.

Лишь малая часть опрашиваемых из числа носителей точных наук — профессиональных физиков, инженеров-электротехников, радиоинженеров и студентов этих направлений — смогут дать внятный ответ на этот вопрос, а некоторые из них готовы прочитать с ходу целую лекцию на эту тему.

Определение индуктивности

В физике индуктивность, или коэффициент самоиндукции, определяется как коэффициент пропорциональности L между магнитным потоком Ф вокруг проводника с током и порождающим его током I или — в более строгой формулировке — это коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током:

Ф = L·I

или

L = Ф/I

Для понимания физической роли катушки индуктивности в электрических цепях можно использовать аналогию формулы энергии, запасаемой в ней при протекании тока I, с формулой механической кинетической энергии тела.

При заданной силе тока I индуктивность L определяет энергию магнитного поля W, создаваемого этим током I:

= 1/2 ·
L
·
I
2

Аналогично, механическая кинетическая энергия тела определяется массой тела m и его скоростью V:

= 1/2 ·
m
·
V
2

То есть индуктивность, подобно массе, не позволяет энергии магнитного поля мгновенно увеличиться, равно как и масса не позволяет проделать такое с кинетической энергией тела.

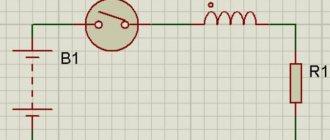
Проведём исследование поведения тока в индуктивности:

Рис. 1. Электрическая схема эксперимента

Рис. 2. Физическая реализация эксперимента

Рис. 3. Осциллограмма тока через индуктивность. Желтая осциллограмма — выход сигнал-генератора, голубая — сигнал на резисторе.

Из-за инерционности индуктивности происходит затягивание фронтов входного напряжения. Такая цепь в автоматике и радиотехнике называется интегрирующей, и применяется для выполнения математической операции интегрирования.

Проведём исследование напряжения на катушке индуктивности:

Рис. 4. Электрическая схема эксперимента

Рис. 6. Осциллограмма напряжения на индуктивности (голубая)

В моменты подачи и снятия напряжения из-за присущей катушкам индуктивности ЭДС самоиндукции, возникают выбросы напряжения. Такая цепь в автоматике и радиотехнике называется дифференцирующей, и применяется в автоматике для корректировки процессов в управляемом объекте, носящих быстрый характер.

Рис. 5. По большому счёту, во всех генераторах электрического тока любого типа, равно как и в электродвигателях, их обмотки представляют собой катушки индуктивности.

Применение катушек в технике

Явление электромагнитной индукции известно уже давно и широко применяется в технике. Примеры использования:

сглаживание пульсаций и помех, накопление энергии;
создание магнитных полей в различных устройствах;
фильтры цепей обратной связи;
создание колебательных контуров;
трансформаторы (устройство из двух катушек, связанных индуктивно);
силовая электротехника использует для ограничения тока при к. з. на ЛЭП (катушки индуктивности, называются реакторами);
ограничение тока в сварочных аппаратах — катушки индуктивности делают его работу стабильнее, уменьшая дугу, что позволяет получить ровный сварочный шов, имеющий наибольшую прочность;
применение катушек в качестве электромагнитов различных исполнительных механизмов;
обмотки электромагнитных реле;
индукционные печи;
установление качества железных руд, исследование горных пород при помощи определения магнитной проницаемости минералов.

Сферы применения

Что такое индуктивность – ясно, но где ее можно использовать? Вообще, найти их можно практически в каждом электроприборе. Например, они повсеместно встречаются в блоках питания.

В источниках тока в процессе работы происходит понижение/повышение напряжения, за что отвечает трансформатор – по сути, 2 или более катушки, которые объединённые последовательно. Причем с увеличением циклической частоты повышается эффективность.

Например, в самолетах используются 400-герцовые трансформаторы, вместо бытовых и промышленных 60 Гц.

Также их можно встретить в:

электрические фильтры;
зарядные устройства;
нагреватели;
электрические магниты;
крупная бытовая техника.

Соленоид

Соленоид отличается от обычной катушки по двум признакам:

Длина обмотки превышает диаметр в несколько раз;
Толщина обмотки меньше диаметра катушки также в несколько раз.

Соленоидальный тип катушки
Параметры соленоида можно узнать из такого выражения:

L=µ0N2S/l,

где:

µ0 – магнитная постоянная;
N – количество витков;
S – площадь поперечного сечения обмотки;
l – длина обмотки.

Важно! Приведенное выражение справедливо для соленоида без сердечника. В противном случае необходимо дополнительно внести множитель µ, который равен магнитной проницаемости сердечника

Чем большую магнитную проницаемость будет иметь сердечник, тем больше увеличится итоговое значение.

Необходимые формулы для расчетов

Чтобы найти индуктивность соленоида, формула применяется следующая:

L= µ0n2V,

где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.

Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:

L = µ0N2S : l,

Будет интересно➡ Что такое автотрансформатор?

где S – это площадь поперечного сечения, а l – длина соленоида.

Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.

ÐÐ°Ð³Ð½Ð¸ÑÐ½Ð¾Ðµ Ð¿Ð¾Ð»Ðµ

«Катушка ниток»

Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.

Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:

I = U : R,

где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.

Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.

Катушку можно разделить на два вида:

С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.

Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:

L = 10µ0ΠN2R2 : 9R + 10l.

А вот уже для многослойной другая формула:

L= µ0N2R2 :2Π(6R + 9l + 10w).

Основные выводы, связанные с работой катушек:

На цилиндрическом феррите самая большая индуктивность возникает в середине.
Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
Индуктивность тем меньше, чем меньше количество витков.
В тороидальном сердечнике расстояние между витками не играет роли катушки.
Значение индуктивности зависит от «витков в квадрате».
Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.

Сборка платы приставки

собрать тестер подключение к мультиметру для измерения индуктивности без проблем в домашних условиях можно, имея базовые знания и навыки в области радиотехники и пайки микросхем.

В схеме можно использовать транзисторы КТ361Б, КТ361Г и КТ3701 с любыми буквенными обозначениями, но для более точных измерений лучше использовать транзисторы с маркировкой КТ362Б и КТ363.

Эти транзисторы установлены на плате в позициях VT1 и VT2. В положение VT3 необходимо установить кремниевый транзистор с pnp структурой, например, КТ209В с любой буквенной маркировкой. Позиции VT4 и VT5 предназначены для буферных усилителей.

Подходит большинство высокочастотных транзисторов, с параметрами h21E для одного не ниже 150, а для другого выше 50.

Любой высокочастотный кремниевый диод подойдет для позиций VD и VD2.

Резистор можно выбрать МЛТ 0,125 или аналогичный. Конденсатор С1 берется номинальной емкостью 25330 пФ, так как он отвечает за точность измерения, и его величину следует выбирать с отклонением не более 1%.

Такой конденсатор может быть изготовлен путем объединения термостабильных конденсаторов разной емкости (например, от 2 до 10 000 пФ, от 1 до 5100 пФ и от 1 до 220 пФ). Для других локаций подходят любые малогабаритные электролитические и керамические конденсаторы с допустимым разбросом в 1,5-2 раза.

Контактные провода к плате (позиция X1) могут быть припаяны или подключены с помощью пружинных зажимов для «акустических» проводов. Разъем X3 предназначен для подключения приставки к мультиметру (частотомеру).

лучше всего использовать более короткий провод для «бананов» и «крокодилов», чтобы уменьшить влияние индуктивности на показания измерений. В том месте, где провода припаяны к плате, соединение необходимо дополнительно зафиксировать каплей горячего клея.

Если вам нужно отрегулировать диапазон измерения, вы можете добавить к карте разъем для переключателя (например, трех диапазонов).

Основные формулы для вычисления вектора МИ

Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.

Закон Био-Савара-Лапласа

Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.

Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.

Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB

dB = µ0 *I*dl*sin α /4*π*r2,

где

dB – магнитная индукция, Тл;
µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
I – сила тока, А;
dl – отрезок проводника, м;
r – расстояние до точки нахождения магнитной индукции, м;
α – угол, образованный r и вектором dl.

Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме

Закон Био-Савара-Лапласа

Существуют формулы, описывающие этот закон для отдельных случаев МП:

поля прямого перемещения электронов;
поля кругового движения заряженных частиц.

Формула для МП первого типа имеет вид:

В = µ* µ0*2*I/4*π*r.

Для кругового движения она выглядит так:

В = µ*µ0*I/4*π*r.

В этих формулах µ – это магнитная проницаемость среды (относительная).

Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.

Принцип суперпозиции

Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:

B→= B1→+ B2→+ B3→… + Bn→

Принцип суперпозиции

Теорема о циркуляции

Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.

Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.

Другое название теоремы – закон Ампера, описывающий циркуляцию МП.

Математически теорема записывается следующим образом.

Математическая формула теоремы о циркуляции

где:

B→– вектор магнитной индукции;
j→ – плотность движения электронов.

Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.

Магнитный поток

Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):

108 Мкс = 1 Вб.

Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.

Формула для расчёта имеет вид:

φ = |B*S| = B*S*cosα,

где

В – скалярная величина градиента магнитной индукции;
S – площадь пересекаемой поверхности;
α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).

Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900)

Магнитный поток

Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:

Рисунок 1.21.2. Вычисление энергии магнитного поля.

В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:

Wм=ΦI2=LI22=Φ22L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:

Wм=μ0·μ·n2·I22V=B22μ0·μV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

ÐÐ¸Ð´Ñ ÐºÐ°ÑÑÑÐµÐº

Вариометр

Что такое катушка, показано выше на простых примерах. На практике для обозначения однотипных групп применяют специфическую терминологию. Вариометром, например, называют деталь с переменной индуктивностью. В типовой конструкции применяют две катушки, установленные одна внутри другой. Необходимый результат получают регулировкой взаимного положения функциональных компонентов. Для перемещения применяют ручной привод или автоматизированный механизм с внешней схемой управления.

К сведению. Не следует путать определения. Мультипликаторная катушка, например, – это приспособление для рыбной ловли. Такое устройство будет обладать индуктивностью при наматывании лески из проводящего материала. Однако в радиотехнических схемах подобные устройства не используют.

Мультипликаторные катушки

Особенности других конструкций:

Дроссель обеспечивает высокое сопротивление цепи переменному току, поэтому такой пассивный индуктивный элемент часто применяют для создания фильтров. При подключении к сети питания 220В/ 50 Гц используют железные сердечники. При повышении частоты – ферритовые аналоги.
Контурные катушки магнитные устанавливают в комбинации с конденсаторами для создания схем с определенной полосой пропускания.
Электрическим реактором называют крупные конструкции, которые применяют в силовых сетях.
Сдвоенные катушки применяют для разделения цепей по постоянной составляющей.

Токовый реактор ограничивает сильный ток, предотвращает развитие аварийной ситуации при КЗ
Выше отмечены типовые области применения элементов с индуктивными характеристиками. Они пригодны для создания фильтров, ограничения тока и разделения цепи прохождения постоянных и переменных составляющих сигнала. Магнитное поле катушки с током распространяется в пространстве. Чтобы предотвратить паразитное воздействие, отдельные компоненты размещают на достаточном расстоянии.

Приставка ВЧ детектор к мультиметру

Простейшая схема приставки к цифровому мультиметру для измерения переменного тока ВЧ. Подходит для измерения мощности звукового усилителя или радиопередатчика. Мультиметр должен быть интегрирован с простой внешней измерительной головкой, содержащей высокочастотный детектор на германиевых диодах. Эта схема выпрямляет и фильтрует переменное напряжение сигнала, преобразовывая его в легко измеряемую постоянную.

Входная емкость ВЧ-головки менее 3 пФ, что позволяет подключать ее непосредственно к каскадной схеме. Можно использовать советские высокочастотные диоды Д9, ГД507 или Д18. ВЧ-головка собрана в экранированном корпусе, на котором расположены клеммы для подключения зонда или проводов к измеряемой цепи. Связь с тестером должна осуществляться с помощью экранированного телевизионного кабеля.

ÐÑÑÐ¾ÑÐ¸Ñ

Общие сведения

Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.

Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.

Среди основных свойств индуктивности выделяются:

Величина параметра никогда не может быть меньше нуля.
Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.

Цифровой мультиметр

В отличие от аналоговых, этот мультиметр позволяет легко определять интересующие величины, при этом его точность измерения намного выше, чем у стрелочных приборов.

Кроме того, наличие переключателя между различными характеристиками электричества исключает возможность спутать одно значение или другое, поскольку пользователю не нужно понимать градацию шкалы индикации.

Результаты измерений отображаются на дисплее (в старых моделях — светодиодный, а в современных — жидкокристаллический). По этой причине цифровой мультиметр удобен для профессионалов и прост и интуитивно понятен для начинающих.

Свойства магнетизма

Магнитное поле, как и любое другое физическое явление на Земле, имеет свои характеристики:

Источник возникновения – движущиеся электрические заряды.
Индукция магнитного поля – основная силовая его характеристика, которая существует в каждой отдельной его точке и является направленной.
Его влияние ограничивается магнитами, движущимися зарядами и проводниками тока.
Оно разделяется учеными на два типа: постоянное и переменное.
Человек без специальных приборов не может почувствовать воздействие магнетизма.
Это электродинамическое явление, ведь источник его происхождения – движущиеся частицы электрического тока. И только такие же частицы могут быть подвержены влиянию магнитного поля.
Траектория движения заряженных частиц может быть лишь перпендикулярной.

Линии магнитной индукции

Сама индукция магнитного поля характеризуется определенным направлением, представляющим собой линии, отображаемые графически. Эти линии, также получили название магнитных линий, или линий магнитных полей. Так же, как и магнитная индукция, ее линии имеют собственное определение. Они представляют собой линии, к которым проведены касательные во всех точках поля. Эти касательные и вектор магнитной индукции совпадают между собой.

Однородное магнитное поле отличается параллельными линиями магнитной индукции, совпадающими с направлением вектора во всех точках.

Если же магнитное поле является неоднородным, произойдет изменение вектора электромагнитной индукции в каждой пространственной точке, расположенной вокруг проводника. Касательные, проведенные к этому вектору, приведут к созданию концентрических окружностей вокруг проводника. Таким образом, в данном случае, линии индукции будут выглядеть в виде расширяющихся окружностей.

Аналоговый мультиметр

Этот тип мультиметра отображает показания измерений с помощью стрелки, под которой находится дисплей с различными шкалами значений. Каждая шкала показывает показания того или иного измерения, которые подписываются прямо на табло.
Но для новичков такой мультиметр будет не лучшим выбором, так как разобраться во всех символах, которые есть на дисплее, довольно сложно. Это может привести к неправильному пониманию результатов измерения.

Материал сердечника

Как и в предыдущем примере, для вычисления индукции катушки с сердечником в представленные выше формулы добавляют множитель относительной магнитной проницаемости «m

L = m0 * m * N2 * (S/l) = m0 * m * n2 * V.

С помощью этого коэффициента учитывают ферромагнитные свойства определенного материала.

Если для примера взять бесконечный (очень длинный) прямой провод с круглым сечением, то он будет обладать определенной индуктивностью:

L = (m0/2π) * l *(mc * ln(l/r) +1/4m,

где:

mc – магнитная проницаемость (относительная) среды;
r – радиус, который намного меньше длины (l) проводника.

Однако простые зависимости действуют только до определенной частоты. С определенного уровня волны малой длины начинают распространяться в поверхностной части проводников (скин-эффект). Дополнительно приходится учитывать влияние вихревых составляющих, экранирующих излучение и меняющих силовые параметры поля.

Современные магнитные материалы

Катушка будет работать в точном соответствии с расчетом, если правильно подобраны все функциональные компоненты конструкции. Как показано выше, существенное значение имеют параметры сердечника. Ниже отмечены важные особенности соответствующих материалов:

Сталь с низким содержанием примесей стоит недорого. Ее рекомендуется применять в цепях постоянного тока, так как при повышении частоты значительно увеличиваются потери.
В специальные сорта (трансформаторную сталь) добавляют кремний. Для уменьшения вредного влияния поверхностных эффектов сердечник собирают из пластин. Однако и такие решения не следует использовать при частоте более 1 кГц.
Сплавы из железа с никелем отличаются увеличенной магнитной проницаемостью. Рабочий диапазон – до 80-120 кГц.
Порошковые материалы создают со слоем диэлектрика на поверхностях отдельных микроскопических гранул. Они хорошо приспособлены для работы с высокочастотными сигналами, однако не обладают большой магнитной проницаемостью.
Ферриты – это материалы, созданные на основе керамических компонентов. Они отличаются хорошими техническими характеристиками, малыми потерями. Следует учитывать значительную зависимость от температуры, а также ухудшение рабочих параметров при длительной эксплуатации.

Измерение индуктивности катушки, созданной из медного провода на ферритовом сердечнике

Обозначение и единицы измерения

Сопротивление тока: формула

В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Джозеф Генри

Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.

Как может обозначаться индуктивность в других системах:

В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
В системе СГСЭ – в статгенри.