О собственной емкости однослойной катушки индуктивности

Всех приветствую, продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса — резисторы и конденсаторы.

СОДЕРЖАНИЕ

В зависимости от назначения катушки индуктивности различают:

— контурные катушки (образующие совместно с конденсаторами колебательный контур);

— катушки связи (передающие высокочастотные колебания из одной цепи в другую);

— высокочастотные дроссели (катушки индуктивности, преграждающие путь токам высокой частоты).

[/td]

По конструктивным признакам катушки могут быть разделены на цилиндрические, спиральные, тороидальные, однослойные, многослойные, с сердечником или без сердечника, экранированные, с постоянной или переменной индуктивностью.

На принципиальных электрических схемах рядом с условным графическим изображением катушки индуктивности помещают ее символическое буквенное обозначение (латинская прописная буква L) с порядковым цифровым (иногда буквенным) индексом. Значение индуктивности на схеме обычно не указывают (рис. 4.1).

Рис. 4.1. Обозначения катушек индуктивности на схемах

Дроссели имеют такое же графическое изображение, но обозначаются буквами Др.

Основные параметры высокочастотных катушек:

Индуктивность характеризует количество энергии магнитного поля, запасаемого катушкой, при протекании по ней электрического тока. Единица измерения индуктивности — генри (Гн) и ее доли: миллигенри (мГн = 10 -3 Гн) и микрогенри (мкГн = 10 -6).

В радиотехнической аппаратуре используются высокочастотные катушки с индуктивностью от долей мкГн до десятков мГн. Индуктивность катушки зависит от ее формы, размеров и числа витков, а также от свойств сердечника или экрана.

Добротность — отношение реактивного сопротивления катушки к ее активному сопротивлению потерь:

QL = 2 π F L / r,

где r — эквивалентное сопротивление потерь в катушке на частоте f.

По аналогии с конденсаторами потери энергии в катушках индуктивности можно выразить тангенсом угла потерь:

tgδ = r / 2 π F L = 1 / Q.

В большинстве радиотехнических устройств используют катушки с добротностью от 40 до 200.

Собственная емкость является паразитным (побочным) параметром катушки индуктивности, она увеличивает потери, уменьшает стабильность, коэффициент перестройки контура по частоте.

Температурный коэффициент индуктивности характеризует относительное изменение индуктивности катушки при изменении температуры на 1°С:

ТКИ = αL = DL(T0) • DT.

Обычные цилиндрические катушки имеют ТКИ = 30…50-10-6 1/°С, а катушки с керамическим каркасом — 8…16-10-6 1/°С.

Стабильность параметров катушек индуктивности зависит также от влажности, величины атмосферного давления и т.п.

Промышленность не выпускает, как правило, типовые высокочастотные катушки. Поэтому для аппаратуры различного назначения изготавливаются по возможности оптимальные индуктивные элементы.

График зависимости тока и ЭДС самоиндукции от времени

Графически характер изменения тока в цепи и ЭДС самоиндукции с течением времени выглядит так:

Зависимость тока и ЭДС самоиндукции в катушке в цепи переменного тока

Из графика видно, что ЭДС самоиндукции тем больше, чем выше скорость изменения силы тока. В начале периода (участок вблизи т.1 на графике) сила тока возрастает быстро, потому и ЭДС самоиндукции здесь максимальна. К концу первой четверти периода (т. 2) скорость изменения снижается почти до нуля (синусоида принимает горизонтальное положение), после чего сила тока все стремительнее уменьшается (участок между т. 2 и т. 3).

Соответственно, ЭДС самоиндукции снижается в т. 2 до нуля, а затем снова возрастает, но при этом меняет знак на противоположный: теперь она противодействует падению силы тока, то есть ток и ЭДС по знаку совпадают. В следующем полупериоде картина повторяется.

Расчет индуктивности некоторых типов высокочастотных катушек

Приведем расчетные формулы для наиболее часто используемых конструкций.

Индуктивность прямолинейного провода с круглым сечением. Сюда относятся индуктивные элементы ДЦВ диапазона, оценка индуктивности проволочных выводов резисторов, конденсаторов, активных элементов:

Lпр = 0,002l(ln [4l/d]-1,75); lLпрl = мкГн,

где [l] = см — длина провода; d = см — диаметр провода без изоляции.

Индуктивность круглого витка из провода круглого сечения. Используют для оценки индуктивности рамочных (резонансных) антенн, катушек связи и т.п.:

Lкр = 0,00628В (ln [8D/d]-1,75),

где [D] = см — диаметр витка.

Индуктивность замкнутого геометрического контура всегда будет меньше индуктивности прямого провода той же длины. Наибольшей индуктивностью обладает тот из замкнутых геометрических контуров одинакового периметра, который имеет наибольшую площадь. Следовательно, наибольшая индуктивность будет у контура, имеющего форму окружности.

Индуктивность однослойной цилиндрической катушки (рис. 4.2).

Рис. 4.2. Элементы однослойной цилиндрической катушки

Если длина намотки l = т • N (N — число витков) соответствует неравенству l >> D, то приемлема формула

L = π2 · D2 N2 10-3 / l мкГн.

Если длина намотки катушки соизмерима с ее диаметром, то вводится поправочный коэффициент L0. Значение этого коэффициента находят по графику, изображенному на рис. 4.3, а величину индуктивности определяют из выражения

L = L0 • N2 • D • 10-3мкГн,

Рис. 4.3. Графическая зависимость поправочного коэффициента

Индуктивность многослойной цилиндрической катушки. Для получения больших значений индуктивности используют многослойные катушки. Индуктивность таких катушек можно определить по предыдущей формуле, но поправочный коэффициент L0 (рис. 4.4) будет зависеть от соотношения толщины намотки к наружному диаметру t/D.

Рис. 4.4. Поправочный коэффициент для многослойной катушки

Индуктивность катушки с сердечником. Получить оптимальное значение индуктивности и добротности, обеспечить точную установку индуктивности позволяет применение сердечников. Индуктивность катушки с сердечником LС = μСL, где L — индуктивность той же катушки без сердечника; μС — действующая магнитная проницаемость. Если μ — магнитная проницаемость материала, из которого выполнен сердечник, то отношение Кμ = μс/μ — коэффициент использования магнитных свойств. Он зависит от конструкции катушки и определяется экспериментально.

Для ферромагнетиков (ферриты, карбонильное железо) μс > 1, для диамагнетиков (латунь, медь, алюминий) μс < 1. Таким образом, используя ферромагнетики, повышают индуктивность катушки, а используя диамагнетики, понижают ее.

Индуктивность тороидальной катушки (с кольцевым сердечником) определяют по формуле

Lтор = 0,00628 • μ • N2 (D — √D2T — Dв),

где DТ — диаметр осевой линии тора, см; DВ — средний диаметр витка; μ — начальная магнитная проницаемость материала тора.

Индуктивность экранированной катушки. Экранирование выполняют или шунтированием магнитного поля ферромагнитным экраном с большой относительной магнитной проницаемостью или вытеснением магнитного поля экраном из диамагнетика (медь, латунь, алюминий). Для экранирования ВЧ катушек используют, как правило, второй способ.

Индуктивность цилиндрической катушки с алюминиевым цилиндрическим экраном

L = L • [1-(D/Dэ)3] • [1-(I/2Iэ)2],

где L — индуктивность катушки без экрана; D — диаметр обмотки; DЭ -диаметр экрана; l — длина намотки; lЭ — длина экрана. Добротность экранированной катушки всегда ниже, а собственная емкость выше катушки без экрана.

Индуктивности и емкости

Итак, для начала немного о конденсаторах. Самый простой из них-две металлические пластины, расположенныена некотором расстоянии друг от друга (рис. 1). Если к такому элементу подсоединить батарейку, то он через некотороевремя зарядится до того же напряжения, что и батарейка.При этом на пластинах конденсатора будут сосредоточеныэлектрические заряды разного знака (рис. 1). Чем большеенапряжение будет приложено между обкладками, тем больше будет величина электрического заряда пластин. Посколькумежду пластинами находится воздух, а на практике чаще всего какой-либо диэлектрик (непроводящий материал), постоянный ток в цепи на рис. 1 протекать не может. В качестведиэлектрика обычно используются такие материалы, как бумага, слюда, керамика, различные органические пленки и некоторые другие. От типа диэлектрика зависят свойства конденсаторов (в первую очередь частотные), о чем мы дополнительно поговорим в рекомендациях по их выбору. Конечно, на практике через заряженный конденсатор все-таки протекает небольшой ток утечки, вызванный неидеальностью диэлектрика.

Рис. 1

Собственно электроемкость есть физическая величина, характеризующая способность конденсатора накапливать (запасать) электрическую энергию. Сухим физико-математическим языком многих учебников говорится, что электроемкость С=q/Uc — это коэффициент пропорциональности между зарядом конденсатора q и напряжением на нем Uc=E, где Е- напряжение источника. Это утверждение, как и многие аналогичные, строго с математической точки зрения, однако, к сожалению, не отражает физической природы явления.

Емкость, как известно, измеряется в долях фарада (единица названа в честь выдающегося физика Майкла Фарадея). При емкости конденсатора в один фарад, электрический заряд на любой из его пластин составил бы один кулон, при напряжении между обкладками в один вольт. На практике емкости, как правило, измеряют в микрофарадах, нанофарадах и пикофарадах.

Емкость конденсатора зависит от формы и геометрических размеров пластин, а также расстояния между ними и параметров диэлектрика. Так, емкость плоского конденсатора, изображенного на рис. 1, определяется как С=ε0εS/d, где ε0 — электрическая постоянная, равная 8,85·1О12 Кл2/(Нм2); ε-диэлектрическая проницаемость диэлектрика; d ~ расстояние между обкладками; S — площадь обкладок. Физический смысл этой формулы вполне очевиден — чем больше площадь пластин и чем ближе друг к другу они расположены, тем больше емкость конденсатора. Отсюда можно сделать важный вывод — при параллельном соединении конденсаторов их емкости складываются, поскольку общая площадь пластин при этом увеличивается. А емкость последовательно соединенных конденсаторов определяется также как сопротивление параллельно включенных резисторов, т.е. итоговая емкость окажется меньше, нежели емкости каждого из последовательно включенных конденсаторов. При этом напряжение распределяется между конденсаторами пропорционально их емкости.

Рис. 2

Рис. 3

В заряженном конденсаторе запасена электрическая энергия Wэл = CU2c/2. Однако, накопление электрического заряда и, соответственно, энергии происходит не мгновенно. В электрической цепи, показанной на рис. 2, в момент замыкания ключа начинает протекать ток заряда, ограниченный сопротивлением R, во много раз превосходящем по величине внутренне сопротивление источника, которым в этом случае можно пренебречь. Тогда ток заряда определяется из закона Ома: Iз=E/R. Напряжение на емкости при этом отсутствует Uc=0 (конденсатор до замыкания ключа, естественно, был не заряжен). В процессе заряда конденсатора ток в цепи уменьшается, а напряжение на конденсаторе возрастает и стремится к Uc=Е. Это проиллюстрировано на графиках (рис. 3) Аналогичным образом происходит разряд конденсатора в цепи на рис. 4.

Рис. 4

Рис. 5

Здесь ток разряда в момент замыкания ключа скачком возрастает от нуля до величины фаз iраз=E/R, а затем снова плавно падает до нуля. Напряжение на конденсаторе при этом плавно падает от Uc=Е до Uc=0 (рис. 5.). При разряде конденсатора вся энергия, запасенная в нем, переходит в тепловую энергию, рассеиваемую на резисторе. Разряд и соответственно расход энергии, также как и заряд, не происходят мгновенно, а занимают определенное время. Это правило называют законом коммутации, который применительно к цепям с емкостью обычно формулируют так: напряжение на емкости мгновенно измениться не может. Действительно, при разряде конденсатора на резистор, напряжение на нем изменяется плавно: Uc = E·EXP(-t/RC). Здесь функция ЕХР(х) — показательная функция еx (число Эйлера е=2,718), чаще называемая экспонентой; а величину RC обычно называют постоянной времени и обозначают греческой буквой τ (тау). Действительно, от этой величины зависит длительность разряда. Процессы заряда и разряда конденсатора являются частными случаями переходных процессов.

Теперь переидем к индуктивности. Катушка индуктивности или дроссель также являются накопителями энергии, только здесь, в отличие от конденсатора, энергия электрического тока преобразуется в энергию магнитного поля. Как известно из физики, вокруг проводника с током образуется магнитное поле, т.е. электрическое поле порождает магнитное. Если проводник свернуть в катушку, то магнитное поле возрастет. Это поле пропорционально количеству витков в катушке.

Интенсивность магнитного поля характеризуется величиной магнитного потока Ф и протекающим через катушку током IL. Способность катушки (или проводника с током) накапливать энергию магнитного поля и характеризует величина индуктивности L, которая опять-таки математически строгим языком является коэффициентом пропорциональности между магнитным потоком и протекающим через катушку электрическим током, его порождающим L = Ф/IL Эта величина зависит только от параметров катушки и измеряется в генри (Гн).

Катушка индуктивностью в один генри при протекании через нее тока в один ампер создает магнитный поток величиной в один веббер (единица измерения магнитного потока). На практике индуктивность катушек обычно намного меньше величины 1 Гн и измеряется в милигенри, микрогенри и наногенри. В цепях постоянного тока сопротивление катушки определяется резистивными потерями в образующем ее проводнике и на ней не падает почти никакого напряжения. При этом, запасенная в катушке энергия магнитного поля может быть вычислена следующим образом: WL=L·IL2/2. Индуктивность (в микрогенри) однослойной катушки (рис. 6) можно рассчитать по следующей известной формуле: L(мкГн)=N2·r2/(9r+10l),где N — число витков, r — радиус витка (каркаса), l — длина намотки Для многослойных катушек существуют свои расчетные формулы. Часто с целью увеличения индуктивности в катушки вводят специальные сердечники из магнито-электриков -феррита, пермалоя, альсифера и т.п.

Рис. 6

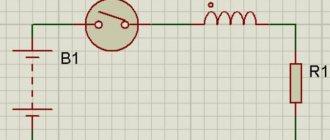
Таким образом, катушка, как и конденсатор, является накопителем энергии. В этом случае на цепи с индуктивностями также должен распространяться закон коммутации, который на сей раз будет звучать так: ток в катушке индуктивности мгновенно изменяться не может. Действительно, при замыкании ключа в цепи на рис. 7 напряжение на катушке изменится скачком до величины E (а затем будет плавно падать до нуля), а ток будет медленно нарастать по тому же закону экспоненты (рис. 8.) от нуля до величины IL= E/R.

Рис. 7

Рис. 8

Так, в цепи на рис. 9 при замыкании ключа сначала загорится лампочка, включенная в ветвь с резистором, а затем, плавно увеличивая яркость, лампочка в индуктивной цепи. Это явление вызвано тем, что аналогично тому как электрическое поле порождает магнитное, так и магнитное, в свою очередь, порождает электрическое. Это утверждение справедливо только для переменного магнитного поля. Это наглядно иллюстрирует известный опыт (рис. 10), когда при перемещении постоянного магнита вдоль катушки в ее внешней цепи протекает ток. Так происходит и в нашем случае: при замыкании ключа через катушку начинает протекать небольшой ток, вызывающий появление около ее витков магнитного потока, изменяющегося пропорционально нарастанию тока. В свою очередь, этот изменяющийся магнитный поток приводит к появлению на катушке электродвижущей силы самоиндукции, включенной согласно закону Ленца встречно силе, вызвавшей ток. Тогда катушка будет оказывать сопротивление нарастанию тока, ровно как и его спаду. Из физики можно привести массу примеров того, когда система противодействует изменению своего стационарного состояния, и сопротивление катушки изменению тока — один из них. В процессе нарастания тока в катушке запасается энергия, а при его спаде, соответственно, тратится. В случае, если резко разомкнуть цепь на рис. 7, через ключ проскочит сильная искра, вызванная ни чем иным, как электродвижущей силой самоиндукции.

Рис. 9

Рис. 10

Рассмотрим, как ведут себя емкость и индуктивность в цепях переменного (синусоидального) тока. Пусть в цепь переменного тока включена емкость (рис. 11). Каждый раз при смене полярности напряжения конденсатор будет перезаряжаться, т.е. знак заряда каждой из его обкладок будет изменяться два раза период переменного напряжения. Если длительность процессов заряда и разряда значительно превосходит период изменения напряжения, ток в цепи также будет изменяться по синусоидальному закону, однако напряжение на конденсаторе отстает по фазе от тока на 90° (рис. 12), что и не удивительно, поскольку конденсатор препятствует резкому изменению напряжения. При этом в процессе каждого заряда-разряда конденсатор будет то накапливать электрическую энергию, то отдавать некоторую ее часть во внешнюю цепь. В большинстве случаев в конденсаторе, включенном в цепь переменного тока, постоянно накоплена определенная электрическая энергия. В цепи с индуктивностью (рис. 13), наоборот, ток отстает по фазе от напряжения на 90° (рис. 14). Это тоже соответствует вышеизложенным рассуждениям -катушка оказывает сопротивление любым изменениям тока. При протекании через катушку переменного тока в ней будет запасаться энергия переменного магнитного поля, приводящая к появлению переменной электродвижущей силы самоиндукции, препятствующей протеканию переменного тока.

Рис. 11

Рис. 12

Итак, катушка в цепи переменного тока оказывает ему сопротивление в результате наведенной переменнои электродвижущей силы самоиндукции. В то же время и конденсатор, запасая в себе электрическую энергию, оказывает сопротивление переменному току. Оба этих сопротивления называют реактивными и обозначают буквой X. В отличие от резистивного (активного) сопротивления, на реактивном не рассеивается никакой тепловой энергии, а лишь запасается энергия в виде электрического или магнитного поля.

Рис. 13

Рис. 14

Реактивные сопротивления катушки XL = j·2πf·L и конденсатора ХC = -j/2πf·C зависят от частоты f протекающего переменного тока. Мнимая единица j учитывает фазовый сдвиг 90° между током и напряжением, а знак «-» показывает, что напряжения на последовательно включенных емкости и индуктивности противофазны. Действительно, при расчете полного комплексного сопротивления цепи, содержащей индуктивности и емкости, индуктивные сопротивления необходимо складывать со знаком «+», а емкостные, наоборот, со знаком «-«. На рис. 15 показана зависимость реактивных сопротивлений индуктивности и емкости, а также их модулей от частоты. На постоянном токе, как известно, индуктивность не оказывает никакого сопротивления, а сопротивление конденсатора, наоборот, стремиться к бесконечно большому. С ростом частоты картина резко меняется — сопротивление катушки индуктивности возрастает по линейному закону, а сопротивление конденсатора падает согласно кривой, называемой гиперболой.

Рис. 15

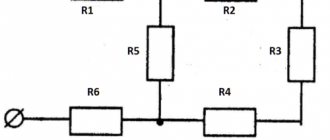
Вышеупомянутые свойства легко пояснить на примере. На рис. 16 приведена принципиальная схема выходной цепи простейшего радиочастотного усилителя. Здесь в цепь питания коллектора транзистора включен блокировочный дроссель L6n, который на рабочей частоте усилителя имеет очень большое сопротивление. Задача этого дросселя не пропустить переменный ток коллекторной цепи транзистора в источник питания, имеющий очень ма ленькое сопротивление. Этот переменный ток должен протекать в нагрузку через разделительный конденсатор Ср, предотвращающий замыкание источника питания на нагрузку (следующий каскад). Этот конденсатор должен выбираться таким образом, чтобы на рабочей частоте усилителя не оказывать практически никакого сопротивления переменному току, т.е. его реактивное сопротивление должно быть по крайней мере на порядок (в 10 раз) меньше сопротивления нагрузки. Для того, чтобы практически весь переменный ток протекал в нагрузку, нужно, чтобы реактивное сопротивление дросселя, наоборот, по крайней мере на порядок превышало сопротивление нагрузки. Однако, поскольку реактивное сопротивление дросселя не является бесконечно большим, незначительная часть переменного тока все же пройдет через него. Во избежание попадания этого тока в источник питания включен блокировочный конденсатор Сбл, обладающий на рабочей частоте очень маленьким реактивным сопротивлением.

Рис. 16

Катушки, дроссели и конденсаторы находят и много других различных применений в радиоэлектронных устройствах. В частности, на них строятся селективные и иные колебательные цепи, о простейших из которых пойдет речь в следующий раз.

В завершении же сегодняшнего рассказа хотелось отметить еще один важный параметр катушек и конденсаторов. Как мы уже говорили, в катушках и конденсаторах имеются потери. В катушке это конечное сопротивление проводника rL, а в конденсаторе — сопротивление утечки диэлектрика rут. Наличие этих потерь приводит к частичному преобразованию запасаемой в катушке и конденсаторе магнитной и электрической энергии в тепловую. Величина этих потерь характеризуется параметром добротность Q=Х/r, который определяется как отношение запасенной энергии к энергии потерь.

Перейдем к более практическим вещам — как выбрать конденсаторы, дроссели, катушки для своей аппаратуры? Для начала о конденсаторах. Здесь важно знать по крайней мере три параметра — электроемкость, рабочее напряжение (а в ряде случаев и предельную реактивную мощность) и частоту (с точностью до: постоянный ток, звуковые частоты, радиочастоты). Независимо от частоты любые конденсаторы следует выбирать на рабочее напряжение (указывается на корпусе), превосходящее ориентировочно в 1,2 раза максимальное значение напряжения, прикладываемое к этому конденсатору в схеме. Не смотря на то, что напряжение пробоя диэлектрика обычно примерно в 1,5 раза превосходит указанное рабочее, такой запас делать все равно необходимо. Что же касается типа диэлектрика, то на сегодняшний день во все радиочастотные цепи в качестве блокировочных и разделительных конденсаторов, а также емкостей фильтров, необходимо устанавливать керамические конденсаторы, диапазон номиналов которых простирается от единиц пикофорад до десятков нанофарад. Следует особо оговорить, что в качество контурных конденсаторов, а также для других частотоизбирательных цепей (фильтров, цепей согласования и т.п.) следует применять конденсаторы с высокой степенью точности величины их емкости (не хуже ±5%), а вот в качестве блокировочных и разделительных элементов применяют более дешевые детали с меньшей точностью. Подстроечные конденсаторы так же, как правило, керамические, а переменные — с воздушным или твердым синтетическим диэлектриком. Большие значения емкостей, как правило, требуются в низкочастотных цепях, где вполне хорошо работают бумажные конденсаторы — герметизированные и т.п. Разброс значений таких конденсаторов составляет от десятков нанофарад да сотен микрофарад. На смену бумажным конденсаторам (с емкостями, не превышающими единиц микрофарад) все чаще приходят танталовые полупроводниковые. Что же касательно слюдяных, то большинство из них в настоящее время сняты с производства из-за своей нетехнологичности. Эти конденсаторы выпускались с величинами емкостей в пределах от сотен пикофарад до десятков нанофарад. Бумажные конденсаторы устанавливают и в цепи токов промышленной частоты (в качестве сетевых фильтров, пусковых конденсаторов двигателей и неоновых ламп и т.п.). Несколько особняком стоят конденсаторы с диэлектриком на основе различных органических пленок. Их можно применять как в низкочастотной, так и в радиочастотной аппаратуре, однако при частотах, не превышающих примерно 50, в редких случаях 100 МГц. Наконец, в цепях постоянного тока (в фильтрах выпрямителей и т.п.) наиболее предпочтительны электролитические конденсаторы, разброс емкостей которых составляет от единиц микрофарад до десятков милифарад (иногда и более). Эти конденсаторы полярны и в цепях переменного тока очень быстро выходят из строя. В виде исключения, их можно устанавливать в цепи усилителей звуковой частоты в качестве разделительных, а также в цепи смещения маломощных каскадов.

Что касается катушек индуктивности и дросселей, то их при изготовлении любительской аппаратуры, как правило, приходится делать самому. Исключение составляют высокочастотные дроссели, которые выпускаются промышленностью на индуктивности порядка десятков — сотен микро-генри. Эти дроссели низкодобротные и ни в коем случае не могут использоваться в качестве контурных катушек и индуктивностей фильтров. Основное их назначение — блокировочные дроссели каскадов усиления радиочастоты малой и иногда средней мощности (при токах в цепях, не превышающих одного-двух ампер). В мощных каскадах передатчиков и другой генераторной аппаратуры устанавливаются самодельные дроссели, которые наматываются толстым медным проводом, способным выдерживать протекающие в этих цепях токи. Это касается и контурных катушек мощных каскадов. Их следует наматывать на теплостойких каркасах без сердечников, поскольку последние сильно разогреваются вихревыми токами высокой частоты и заметно снижают КПД каскада. А вот при намотке контурных катушек и индуктивносетй фильтров маломощных каскадов передатчиков и приемников обычно используют каркасы с сердечниками — чаще всего ферритовыми. Также иногда применяют альсиферовые и латунные (на УКВ) сердечники. В диапазонах KB и УКВ применяют однослойную намотку, а на более низких частотах — многослойную, причем при многослойной намотке желательно применять метод «универсаль» с перекрещиванием витков (как на бобине с нитками или шпагатом), что позволяет уменьшить собственную емкость катушки. Что же касается низкочастотных дросселей (фильтров выпрямителя и т.п.), то их чаще всего наматывают на сердечниках из трансформаторной стали или используют готовые от промышленной аппаратуры.

В заключение расскажем, как при помощи старенького авометра (стрелочного тестера) определить исправность катушек и конденсаторов. Для испытаний конденсаторов тестер следует перевести на максимальный предел измерения сопротивления. Итак, исправный конденсатор емкостью менее 0,1 микрофарад не должен вызывать никакого отклонения стрелки, — в противном случае конденсатор пробит. При испытании конденсатора емкостью 0,1… 10 микрофарад стрелка должна дернуться вправо и быстро вернуться в область бесконечно большого сопротивления. Наконец, при испытании конденсаторов большой емкости (электролитических и т.п.) стрелка тестера должна резко отклониться вправо (почти до нуля сопротивлений), а затем медленно возвратиться обратно. Слабый бросок свидетельствует о потере емкости. К сожалению, при помощи цифровых мультиметров подобное испытание практически невозможно ввиду отсутствия стрелочного индикатора, однако многие из них «умеют» измерять емкость, что существенно упрощает задачу. Для проверки катушек индуктивности и дросселей тестер необходимо перевести на нижний предел измерения сопротивлений. Контурные катушки и высокочастотные дроссели имеют омическое сопротивление, близкое к нулю, а при испытании низкочастотных дросселей (а также обмоток низкочастотных и силовых трансформаторов) тестер покажет сопротивление порядка десятков — сотен Ом. При испытании низкочастотных индуктивных элементов следует избегать касания проводников незащищенными руками, поскольку в момент подсоединения дросселя или трансформатора к тестеру, на зажимах появляется ЭДС самоиндукции значительной величины.

Оптимизация добротности катушек индуктивности

Не менее важным параметром, чем индуктивность, при расчете индуктивных компонентов контуров, фильтров, линий задержек является их добротность.

На заданной частоте добротность катушки индуктивности определяют по формуле

QL = 2 π F L / r,

где r — активное сопротивление потерь, которое имеет несколько составляющих. Сопротивление потерь можно представить в виде суммы

r = r0 + rf + rk + rем + rэкр + rс,

где r0 — сопротивление обмотки постоянному току; rf — высокочастотные потери; rk — потери в материале каркаса; rем — емкостные потери; rэкр — потери в материале экрана; rс — потери в материале сердечника.

Сопротивление высокочастотных потерь в обмотке состоит из потерь, обусловленных поверхностным (скин) эффектом и эффектом близости rf= rскин + rблиз. Обе эти составляющие имеют выраженную зависимость от диаметра провода намотки, как показано на рис. 4.5. Это свойство используется для получения максимальной добротности путем выбора оптимального диаметра провода намотки.

Рис. 4.5. Оптимальный диаметр провода намотки

Диэлектрические потери, возникающие в поле собственной емкости катушки через диэлектрик, имеют ту же природу, что и в конденсаторах и описываются тангенсом диэлектрических потерь на рабочей частоте.

Дросселем высокой частоты называют катушку индуктивности, включаемую в цепь для увеличения сопротивления токам высокой частоты. Основные параметры: zдр — полное сопротивление, R — сопротивление постоянному току, Сдр — собственная емкость. Полное сопротивление на рабочих частотах должно быть большим и иметь индуктивный характер. Собственная емкость дросселя (рис. 4.6) определяет его критическую частоту fкр = 1/(2п(LдрСдр)1/2, ниже которой расположен рабочий интервал частот.

Рис. 4.6. Эквивалентная схема и зависимость полного сопротивления дросселя

Серийно выпускаются ВЧ дроссели типа ДМ с ферритовым сердечником. Интервал индуктивностей 1…500 мкГ. Допустимое значение тока 60 мА.

Самоиндукция

Если через замкнутый контур пропускать переменный ток, можно зарегистрировать с помощью простых экспериментов магнитное поле в окружающей среде. Изменение силовых параметров сопровождается появлением в цепи наведенной электродвижущей силы. Данное явление называют самоиндукцией.

Величину ЭДС можно вычислить по формуле:

Е = -L * (Δi/Δt).

Это выражение показывает зависимость напряжения от изменения тока за единицу времени. Поправочный коэффициент (L) обозначает особенности проводника (индукционной катушки). Знак «-» характеризует инерционные свойства явления.

При пропускании синусоидального сигнала следует учитывать отставание напряжения (векторное выражение) от тока на 90 градусов. Амплитуда будет прямо пропорциональна частоте (w):

E = L * I * w.