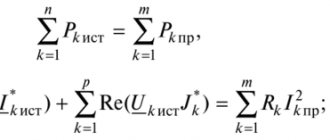Установившиеся процессы в линейных электрических цепях в электротехнике (ТОЭ)

Комплексный метод анализа установившихся процессов в линейных электрических цепях:

Анализ (расчет) электрической цепи состоит в определении отклика цепи (реакции) на входящие воздействия. Под воздействием в данном случае понимается включение в цепь источников напряжения и тока. Откликом в общем случае называют все токи в ветвях и все напряжения на пассивных элементах. Следовательно, рассчитать электрическую цепь — значит, найти все токи и все напряжения в этой цепи.

Для упрощения расчет цепи при гармоническом воздействии производится комплексным методом. Он состоит в том, что при расчете все гармонические функции (оригиналы токов, напряжений, источников) заменяют их комплексными изображениями (символами), а все пассивные элементы представляют их комплексными сопротивлениями. После определения комплексных токов и напряжений (изображений откликов) находят их оригиналы (вещественные мгновенные значения) по формуле Эйлера.

Оригиналы, значения и изображения синусоидальных токов и напряжений

Синусоидальные ток и напряжение а вещественной форме (оригиналы) записываются в виде

где — амплитуды колебаний; — начальные фазы колебаний.

Среднее и действующее значения синусоидально изменяющейся величины. За среднее значение тока и напряжения принимают их среднее значение за полпериода. Среднее значение тока

Аналогично

Действующее значение тока

Аналогично

Мгновенные комплексные значения (изображения, символы) синусоидальных тока и напряжения:

где — комплексная амплитуда тока; — комплексный ток (комплексное действующее значение тока): — комплексная амплитуда напряжения; —комплексное напряжение (комплексное действующее значение напряжения).

Цепь с емкостным элементом

Емкость С

–
это такой параметр, который характеризует способность устройства накапливать электрические заряды q, если к этому устройству приложено напряжение u
.

Емкостной элемент

–
это идеальный конденсатор, представляющий собой две проводящие пластины площадью S, разделенные слоем диэлектрика толщиной d
. Идеальным считается конденсатор, у которого проводимость слоя диэлектрика равна нулю (отсутствует ток утечки) и диэлектрическая проницаемость
ε
является постоянной величиной. Из школьного курса физики известна формула величины емкости идеального плоского конденсатора .

Можно более строго определить емкость С как коэффициент пропорциональности между зарядом q и напряжением u, создавшим этот заряд

(30)

q = Cu
На электрических схемах емкостной элемент изображается двумя параллельными отрезками прямой одинаковой длины (рис. 19).

Если конденсатор подключить к источнику постоянного тока, то произойдет процесс его заряда, в результате чего на проводящих пластинах появится напряжение U

источника, а ток зарядки прекратится, поскольку слой изоляции между пластинами постоянный ток не пропустит.

Иначе ведет себя конденсатор, когда он включен в цепь переменного тока, так как полярность напряжения на его пластинах меняется с двойной частотой питающей сети (при частоте ƒ

= 50 Гц – сто раз в секунду). То есть происходит перезаряд пластин, и по проводам питающей линии протекает переменный ток, обусловленный направленным движением электронов в металлических проводниках.

Что касается слоя диэлектрика, то в нем протекает ток электрического смещения

, связанный с направленной ориентацией зарядов внутри молекул диэлектрика (диполей).

Рассмотрим цепь синусоидального тока с идеальным емкостным элементом (рис. 19).

Предположим, что напряжение на входных зажимах цепи не содержит начальной фазы (ψU

= 0),

(31)

Сделаем подстановку (31) в правую часть равенства (30)

(32)

Как известно, электрический ток (направленное движение зарядов) в общем случае может быть представлен математически как скорость (производная) изменения заряда во времени . С учетом зависимости (32) получим

(33)

Сравнивая равенства (31) и (33), можно убедиться, что в цепи с емкостным элементом ток опережает напряжение на четверть периода

(
π/
2, 90°).

В правой части равенства (33) введем обозначение Im

амплитуды тока

(34)

где – емкостное сопротивление

. Само равенство представляет
закон Ома для амплитудных
значений тока и напряжения. Разделив обе части этого равенства на , получим
закон Ома для действующих значений
:

(35)

Мгновенная мощность цепи с емкостью С

(36)

Средняя за период (активная) мощность Р

(37)

Таким образом, как и в цепи с идеальным индуктивным элементом, в цепи с конденсатором отсутствует необратимый процесс преобразования электрической энергии, а имеет место обмен энергией между конденсатором и питающей сетью.

На рисунке 20а приведена векторная диаграмма амплитудных значений тока Im

и напряжения
Um
для момента времени
t
= 0 с разверткой в графики соответствующих синусоид (рис. 20б), а также с построением графической зависимости мгновенной мощности
p= UIsin
2
ωt
.

Рассмотрим подробнее обратимый процесс преобразования энергии в рассматриваемой цепи. В первую четверть периода Т/

4(рис. 20б) мгновенная мощность положительна, то есть электрическая энергия поступает из сети, и происходит процесс зарядки конденсатора: напряжение на обкладках конденсатора возрастает от 0 до положительной амплитуды +
Um
, электрическая энергия превращается в энергию электрического поля [1].

(38)

Во вторую четверть периода мгновенная мощность отрицательна (p

< 0), и происходит разряд конденсатора: ток меняет полярность, напряжение снижается до нуля, энергия электрического поля (38) превращается в электрическую и возвращается обратно в питающую сеть. Далее происходит аналогичный процесс со сменой полярности пластин конденсатора на противоположную и т.д

Рис. 20

Таким образом, в цепи с емкостным элементом:

1. Ток опережает напряжения на четверть периода

(
π
/2).

2. Закон Ома справедлив только для амплитудных и действующих значений напряжения и тока

.
При этом вводится понятие о емкостном сопротивлении
.

3. Мгновенная мощность пульсирует с двойной частотой относительно среднего значения P = 0

. Это означает, что
процесс преобразования энергии в рассматриваемой цепи имеет обратимый характер
,
то есть происходит обмен энергией между конденсатором и питающей сетью
.

1.8. Цепь с последовательным соединением r

,
L
и
C
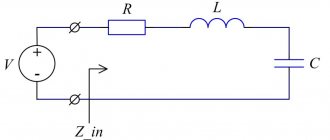
На рисунке 21 показана однофазная электрическая цепь с последовательным включением резистивного r

, индуктивного
L
и емкостного
C
элементов. Цепь замкнута на
источник Е бесконечной мощности
[2], то есть выполняется условие (
U
– действующее значение синусоидального напряжения на входе цепи).

Рис. 21

Запишем в векторной форме второй закон Кирхгофа для действующих значений напряжений применительно к рассматриваемой цепи (рис. 21):

(39)

Равенство (39) как второй закон Кирхгофа читается следующим образом.

В замкнутом электрическом контуре геометрическая сумма векторов действующих значений э.д.с.

(в данном случае это только напряжение )
равна геометрической сумме векторов действующих значений падений напряжения на элементах, образующих этот контур
(здесь эта сумма ).

Поскольку в последовательной цепи (рис. 21) ток I

во всех трех элементах
r, L
и
C
один и тот же, то в соответствии
с законом Ома для участка цепи
можно записать выражения для модулей слагаемых векторов:
Ua
=
Ir
,
UL
=
IxL
,
UC
=
IxC
. В предыдущих разделах (1.5, 1.6, 1.7) были установлены углы сдвига по фазе между вектором тока
I
и соответствующими падениями напряжения
φa
= 0,
φL
= +
π
/2,
φC
= –
π
/2, что позволяет соответствующим образом сориентировать векторы и относительно общего вектора тока и найти суммарный вектор на входе цепи (рис. 21).

Рассмотрим порядок построения векторной диаграммы последовательной цепи (рис. 21) в соответствии с равенством (39).

Ранее (рис. 14, 17 и 20) векторные диаграммы строились для амплитудных значений синусоид тока (или напряжения) применительно к моменту времени t

= 0, когда исходная синусоида имела нулевую начальную фазу (
ψI
= 0 или
ψU
= 0), что позволяло эту синусоиду представлять вектором амплитудного значения в виде горизонтального вектора со стрелкой вправо (рис. 14, 17, 20).

Сохраним этот прием и для рассматриваемой цепи, задавшись синусоидой тока с нулевой начальной фазой ψI

= 0:

(40)

где – амплитуда тока.

Тогда вектор действующего значения тока I

для момента времени
t
= 0 будет направлен, как показано на рисунке 22 а,б.

Выбрав масштаб для напряжений

, изобразим векторы с учетом углов сдвига
φa
= 0,
φL
= +
π
/2и
φC
= –
π
/2, совместив их начала с началом вектора (рис. 22а). При вращении всех четырех векторов против часовой стрелки с угловой частотой
ω
можно убедиться, что проходящую через , показанную на рисунке пунктиром, вначале пересекает вектор , через четверть периода – соответствующие векторы и , а еще через четверть периода – вектор (соответственно
φL
= +
π
/2,
φa
= 0,
φC
= –
π
/2).

Рис. 22

Рассмотрим подробно порядок построения векторной диаграммы последовательной цепи в соответствии с равенством (39), используя известный способ сложения нескольких векторов по правилу многоугольника

.
Согласно этому правилу, выбрав в качестве первого слагаемого один из векторов, остальные слагаемые векторы посредством параллельного переноса совмещают началами с концами предыдущих слагаемых векторов. Соединив начало первого слагаемого вектора с концом последнего, получают суммарный вектор
.

Задавшись направлением вектора , в качестве первого слагаемого принимаем вектор (рис. 22б). В качестве второго слагаемого строим вектор параллельным переносом из рисунка 22а, совместив его начало с концом вектора . Проделав аналогичную операцию с третьим слагаемым , получим результирующий вектор напряжения на входе цепи , соединив начало первого слагаемого вектора с концом третьего (рис. 22б).

Очевидно полученная векторная диаграмма представляет собой графическое решение второго закона Кирхгофа

, поскольку удовлетворяет уравнению (39). Как видно из векторной диаграммы на рисунке 22б, в заштрихованном векторном прямоугольном треугольнике противолежащий углу
φ
катет представляет собой вектор, длина которого
Up
равна алгебраической разности
Up
=
UL
–
UC
, поскольку векторы и находятся в противофазе, то есть сдвинуты на угол 180°. Результирующий вектор получил название «
реактивное напряжение
». Поскольку
UL
=
IxL
,
UC
=
IxC
., то

(41)

где – реактивное сопротивление

Применив к треугольнику напряжений (рис. 22б) теорему Пифагора, получим

(42)

где – полное или кажущееся сопротивление

Перепишем равенство (42) в виде

(43)

которое представляет собой закон Ома для последовательной цепи

, читающийся так:
ток прямо пропорционален напряжению на входе цепи
. Коэффициентом пропорциональности для последовательной цепи является множитель
1
/z.

Как видно из векторной диаграммы (рис. 22б) вектор напряжения опережает вектор тока на угол φ

(с учетом направления вращения векторов против часовой стрелки). Это объясняется тем, что в рассматриваемом случае цепь носит индуктивный характер, то есть
xL
>
xC
и
UL
>
UC
.
Знак такого угла φ принято считать положительным
. Очевидно для рассматриваемого случая можно записать выражение для мгновенного значения синусоиды напряжения

(44)

Разделив все стороны векторного треугольника напряжений (рис. 23а) на одну и ту же величину тока I

, получим подобный исходному скалярный треугольник сопротивлений (рис. 23б) со сторонами

Рис. 23

Если умножить стороны треугольника напряжений на величину тока I

, или стороны треугольника сопротивлений на квадрат тока
I
2, то получим еще один подобный треугольник мощностей (рис. 23в) со сторонами:

=
Ua I
=
I
2
r
–
активная мощность
[Вт];

=
Up I
=
I
2
x
–
реактивная мощность
[вар];

=
U I
=
I
2
z
–
полная или кажущаяся мощность
[ВА].

Как известно размерностью единицы мощности является ватт (Вт), который представляет собой произведение размерностей напряжения и тока [Вт[ = [В]×[А]. Применительно к цепям переменного тока принято различать три типа единицы мощности, хотя их размерность одна и та же:

− Вт

(ватт) – единица активной (средней за период) мощности;

− вар

(вольт-ампер реактивный) – единица реактивной мощности;

− ВА

(вольт-ампер) – единица измерения полной (кажущейся) мощности.

Таким образом понятие мощности в электрической цепи синусоидального тока значительно шире, чем в цепях постоянного тока, хотя единица измерения одна и та же, а именно «ватт».

Очевидно мгновенная мощность р

на входе рассматриваемой последовательной цепи
равна произведению синусоиды напряжения на синусоиду тока
, то есть необходимо перемножить правые части равенств (44) и (40):

(45)

После ряда преобразований правой части равенства (45), подробно рассмотренных в [1], можно получить выражение для мгновенной мощности в виде:

(46)

где P

=
Scosφ
– активная (средняя за период) мощность;

=
UI
– полная (кажущаяся) мощность (рис. 23в).

Как видно из равенства (46), мгновенная мощность р пульсирует с двойной частотой

2
ω относительно средней (активной) мощности Р, причем амплитуда косинусоиды двойной частотыпри φ
¹ 0
больше среднего значения
(
S
>
P
), то есть график мгновенной мощности будет иметь отрицательные участки в пределах угла
φ
¹ 0 (рис. 27б).

Комплексное сопротивление и проводимость цепи

При расчете цели комплексным метолом вводится понятие комплексного сопротивления (проводимости).

Комплексным сопротивлением Z называется отношение комплексного напряжения к комплексному току, вызванному этим напряжением:

Применяют три формы записи комплексное сопротивления:

где — полное сопротивление току; — активное сопротивление; — реактивное сопротивление; — разность фаз напряжения и тока.

Комплексной проводимостью называется отношение комплексного тока к комплексному напряжению

На основании выражения (1.9)

где —полная проводимость; —активная проводимость; — реактивная проводимость.

Составляющие сопротивления и проводимости связаны между собой следующими соотношениями:

Примечание. Понятия комплексное сопротивление и комплексная проводимость могут относиться ко всей цепи, к части цепи или к ее отдельным элементам.

Основные законы токопрохождения в линейных электрических цепях

Закон Ома: Определяет связь между током, напряжением и сопротивлением пассивного элемента (ветви, участка цепи, цепи). Вещественная форма закона применима только для сопротивления:

Закон Ома в комплексной форме справедлив для любого пассивного элемента:

Первый закон Кирхгофа: Определяет баланс токов в любом узле электрической цепи. Его можно представить о вещественной

или в комплексной форме

где — число ветвей, соединенных в данном узле.

Второй закон Кирхгофа. Определяет баланс напряжений в любом замкнутом контуре цепи:

где — число пассивных элементов в замкнутом контуре: —число источников, включенных в данный контур.

Связь между синусоидальными током и напряжением в пассивных элементах

В сопротивлении вещественная форма записи связи между током и напряжением определяется по закону Ома:

В комплексной форме (изображения) определяются выражениями:

В сопротивлении ток и напряжение всегда синфазны, т. е.

В индуктивности напряжение и ток связаны соотношениями:

Запишем эти выражения в комплексной форме:

где — комплексное сопротивление индуктивности; — индуктивное сопротивление;

— комплексная проводимость индуктивности;— индуктивная проводимость.

Из формул (1.20) и (1.21) видно, что ток в индуктивности отстает по фазе от приложенного напряжения на угол .

В емкости напряжение и ток связаны соотношениями:

В комплексной форме выражения (1.22) принимают вид:

где — комплексное сопротивление емкости; — емкостное сопротивление; — комплексная проводимость емкости; — емкостная проводимость.

Из формул (1.22) и (1.23) видно, что ток в емкости опережает по фазе приложенное напряжение на угол .

Диаграммы токов и напряжений

Для большей наглядности при анализе процессов и расчете пеней используют временные и векторные диаграммы.

Временной диаграммой называют графики мгновенных значений токов и напряжений на координатной плоскости вдоль вещественной оси времени (рис. 1.4). Начальная фаза отчитывается ох нуля синусоиды (или от максимума косинусоиды) к началу координат. Начальная фаза положительная, если направление отсчета совпадает с направлением оси времени.

Фазовый сдвиг напряжения и тока отсчитывается по направлению от нуля напряжения к нулю тока. Если это направление совпадает с направлением оси времени, то фазовый сдвиг положительный.

Векторной диаграммой называют совокупность векторов, построенных на комплексной плоскости с соблюдением взаимной ориентации по фазе. Длина вектора пропорциональна aмплетуде колебания.

Все векторы во времени вращаются против часовой стрелки со скоростью . На рис.1.5 показана векторная диаграмма, соответствующая временной диаграмме, приведенной на рис. 1.4.

Начальная фаза отсчитывается от вещественной оси к вектору. Фазовый сдвиг отсчитывается от вектора тока к вектору напряжения. Начальная фаза и фазовый сдвиг положительны, если направление их отсчета совпадает с направлением вращения вектора (против часовой стрелки).

Основные величины и методы расчета электрической цепи переменного синусоидального тока

Определение 1
Переменный электрический ток — это электрический ток, который изменяется по направлению и величине в течении времени (в некоторых случаях изменяется только его величина).

В быту для электроснабжения используется переменный синусоидальный ток.

Определение 2

Синусоидальный электрический ток — это электрический ток, который изменяется во времени по синусоидальному закону.

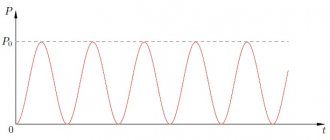
Графически синусоидальный закон изображен на рисунке ниже.

Рисунок 1. График. Автор24 — интернет-биржа студенческих работ

Ты эксперт в этой предметной области? Предлагаем стать автором Справочника Условия работы

$I = Imsin * ((2пt / T) + ф) = Imsin * (wt + ф)$

где: Im – максимальное значение амплитуды электрического тока; T – время, за которое совершается одно полное колебание (период); f – количество колебаний за одну секунду(частота); w – угловая частота; п = 3,14; — ф — начальная фаза

Частота колебаний рассчитывается по следующей формуле:

$f = 1 / Т$

Угловую частоту рассчитывают следующим образом:

$w = 2п * f = 2п / Т$

Любая синусоидальная функция определяется следующими величинами, которые являются основными характеристиками переменного синусоидального тока: